基于悬链线方程的海上横向补给高架索系统静力学分析

郭　飞，李经纬（中国船舶及海洋工程设计研究院，上海 200011）



基于悬链线方程的海上横向补给高架索系统静力学分析

郭飞，李经纬
（中国船舶及海洋工程设计研究院，上海 200011）

摘要:基于悬链线方程，建立考虑高架索长度和自重变化的海上横向补给高架索线形分析静力学模型，探讨高架索单位长度质量和张力大小等参数对高架索线形的影响，研究发现当高架索水平张力与补给品重量比值大于4 时，高架索挠度很小，可以安全输运补给品。

关键词：海上补给；高架索；悬链线方程；线形分析

0　引　言

海上横向补给高架索系统[1]的设计受制于绞车负荷能力、甲板高度、舷侧布置和补给品载荷等因素，在输运过程中应确保补给品不与海面和船体相碰。在实际作业过程中，船舶运动与高架索张力间存在显著的动力学耦合作用[2]，波浪补偿装置控制系统存在一定的滞后效应[3]，这使得高架索系统的精确动态模拟非常复杂。在工程上，常采用静力学方法对高架索的线形进行分析，以保证海上补给作业的安全可靠。张良欣[4–5]等采用分段受力分析的方法得到了高架索挠度表达式，分析了补给品的位置和重量、张力、补给距离对挠度的影响。卢永锦[6]利用弹性力学原理建立了海上横向补给高架索系统的静态分析模型，并通过样机试验验证了其方法的可靠性。余建星等[7]基于上述理论，给出了考虑波峰波谷影响的实际算例，并从高架索张力、钢索挠度和波浪补偿性能等角度提出了适用于小型船舶补给的高架索海上补给装置[8]。

上述文献或假设高架索线形为以悬挂点为拐点的2段直线，或在考虑高架索曲线挠度的同时忽略了高架索自重的变化，因此计算结果并不精确，只适用于集中载荷远大于高架索自重时的估算。本文基于悬链线方程，全面考虑了高架索曲线挠度对高架索线形的影响，得到了更精确的高架索系统静力学分析模型，探讨了高架索线形与高架索自重和张力等参数的关系，并给出了关于高架索最大挠度和最低位置的一般结论。

1　力学分析模型

1.1基本假设

1）忽略船体在波浪中的运动；

2）假设高架索为质量均匀分布的柔性构件，仅受轴向拉伸作用，忽略其轴向弹性变形；

3）假设高架索水平张力恒定；

4）假设补给品在高架索上的运动缓慢平稳。

基于上述假设，可以将高架索上的补给品输运过程视为准静态过程，开展静力学分析。

1.2静力学分析

在补给品输运过程中，悬架索系统可能存在如图1和图2 所示的2种线形：线形 I 和线形 II，其中点 A 为接收点，点 B 为输送点，点 O 为补给品悬挂点。

图1　悬挂点位于接收点之上时的线形 IFig. 1　Cable configuration I when suspension point above receiving point

图2　悬挂点位于接收点之下时的线形 IIFig. 2　Cable configuration II when suspension point below receiving point

图3 为高架索系统为线形 I 时的布置情况和受力分析图。高架索单位长度质量为 w ，接收点 A 和输送点 B 的横向间距为 L，垂向间距为 H。选择点 A 为系统坐标原点，距原点 XG处为货物悬挂点 O，补给品重G， OA 间的垂向距离为 ZG。以点 O 为界，高架索被分成 S1和 S2两段，每段均可视为单独的悬链线。假设FA，FAH，TAV，FB，FBH和 TBV分别为点 A 和 B 处的轴向张力、水平张力和垂直张力，高架索任意位置处横截面上的轴向张力为 T，与水平面的夹角为 θ。

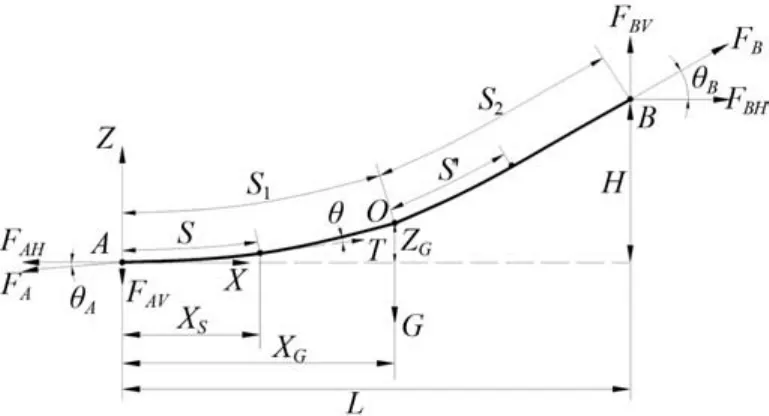
图3　高架索系统受力分析图Fig. 3　Force analysis of the highline cable system

在 S1段内，定义原点为 A 的局部坐标系。取距点A 水平距离为 xs的一段高架索做力学分析，其长度为 S。

由于货物载荷仅在垂直方向，所以高架索各截面处的轴向张力水平分量相同，如式（1），记作 H0。则式（2）可写成：

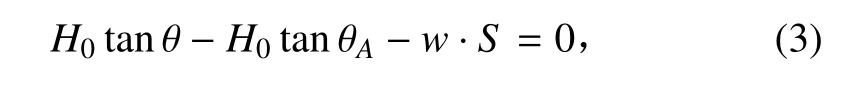
对上式两边进行积分，可得式（5）。

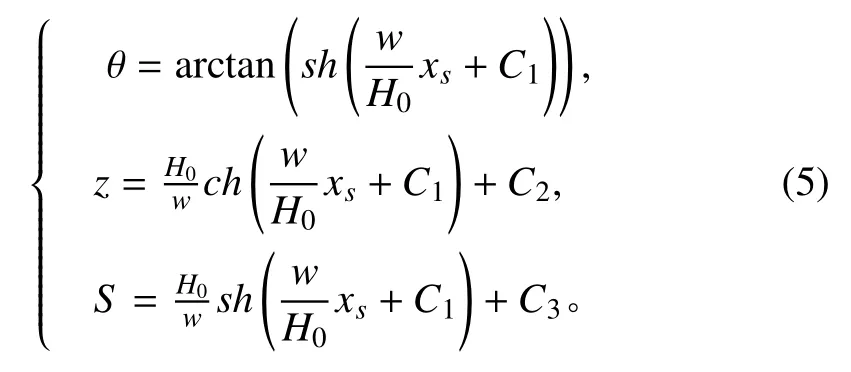
其中系数 C1、 C2和 C3取决于悬链线的边界条件。

上述方法同样适用于 S2段悬链线方程的推导，区别仅在于局部坐标系原点需取在点 O 处。

由此可以得到 S1段和 S2段上点 O 处的切线水平夹角。

再以点 O 处的补给为对象，进行力学分析，可得式（6）：

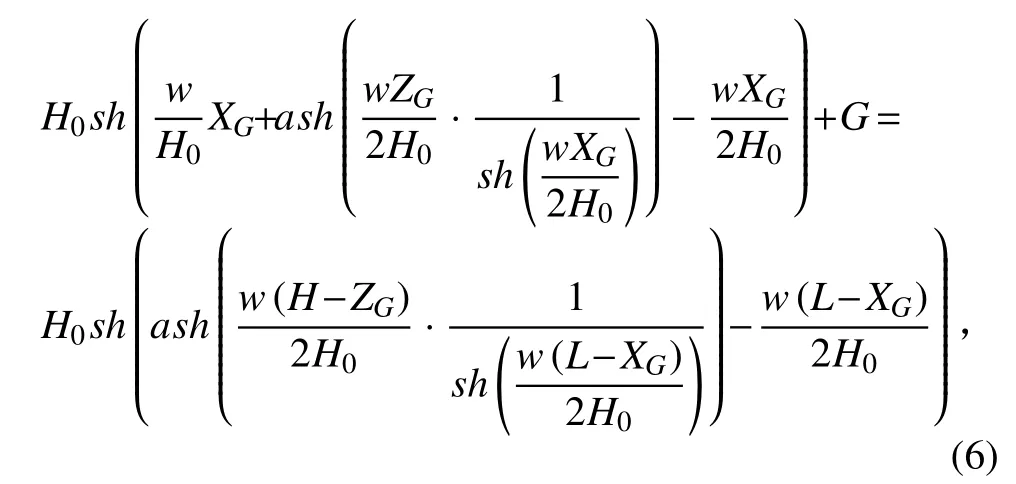
当高架索系统为线形 II 时，同理可得：

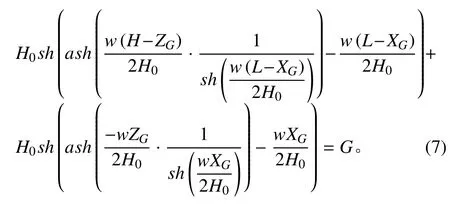
根据式（6）和式（7），通过数值方法可以得到ZG的值，进而得到2段悬链线的数学表达式和高架索各点处的受力情况。

1.3力学模型验证

选取文献[5]中的算例进行对比计算，计算模型的主要参数列于表 1。

图4 为整个补给过程中悬挂点处的挠度曲线，两者几乎完全重合。这表明在当前补给条件下，无论是本文还是文献中的方法均能准确给出悬挂点处的位移。

表1　高架索模型主要参数Tab. 1　Main parameters of the highline cable model

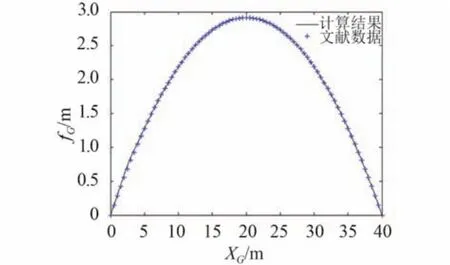
图4　悬挂点挠度曲线对比（H0= 20 kN）Fig. 4　Comparison of deflection curve of suspension point （H0= 20 kN）

但当高架索张力较小（H0= 15 kN）时，2 种方法的区别非常明显。

尤其当悬挂点靠近接收点时，高架索从线形 I 过渡到线形 II，其悬挂点挠度迅速增大，更容易发生补给品落水事故。

文献中的方法忽略了高架索变形带来的自重增加，因此低估了悬挂点位置和高架索变形，在工程实际中可能会带来安全问题，有必要采用本文提出的悬链线方法开展静力学分析。

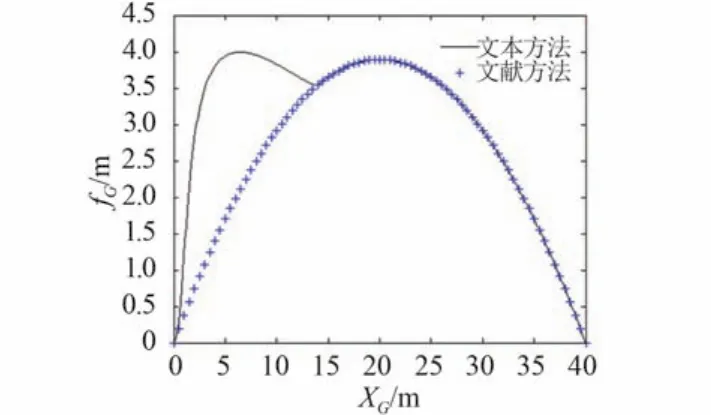
图5　悬挂点挠度曲线对比（H0= 15 kN）Fig. 5　Comparison of deflection curve of suspension point （H0= 15 kN）

2　高架索系统的线形分析

由式（6）和式（7）可知，高架索的线形主要取决于索端横向间距 L、索端垂向间距 H、补给品重G、高架索单位长度质量 W 和水平张力 H0。其中高架索索端横向间距和垂向间距多根据水动力特性[9]和补给俯角[4]要求选取，水平张力多根据补给品和架索重量选择。本文主要探讨架索自重和水平张力对高架索线形的影响，不作特别说明的情况下，高架索参数仍取表 1 中的数值。

2.1架索单位长度质量对线形的影响

图6 为架索单位长度质量变化时不同位置悬挂点处的挠度大小。架索变重相当于补给品重量增加，此时相同悬挂点处挠度增大。当架索自重较小时，挠度较大区域集中在架索中间段，越靠近架索两端，挠度越小；但当架索自重较大时，靠近接收点处的挠度也明显增加。

图7 为相应的不同位置悬挂点处的垂向位置。由于补给端与接收端间存在高度差，所以挠度大的地方并不一定垂向位置低。在文中给出的架索自重变化范围内，垂向位置较低区域始终靠近补给品接收端；随着架索自重增加，相同悬挂点处垂向位置逐渐变低。

图6　不同架索自重时悬挂点挠度云图Fig. 6　Deflection nephogram of suspension point when cable’s weight differs

图8 和图9 进一步给出了架索单位长度质量不同时架索挠度最大值、垂向位置最低位置及其对应的横向位置。随着架索单位长度质量增加，其最大挠度线性增加，但其所在横向位置基本不变，均为架索中间区域；其最低位置呈抛物线减小趋势，但其所在横向位置均在靠近接受端 0～4 m 区间内。

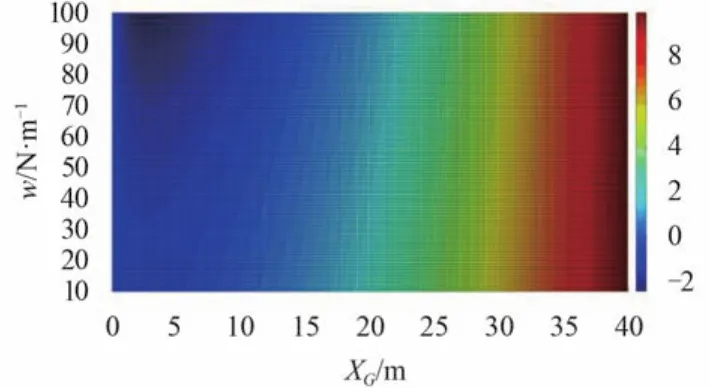
图7　不同架索自重时悬挂点垂向位置云图Fig. 7　Vertical position nephogram of suspension point when cable’s weight differs

2.2架索水平张力对线形的影响

在船舶实际补给过程中，水平张力是最主要的控制变量。图10 和图11 分别给出了水平张力变化时不同位置悬挂点的挠度大小。显然，仅当 H0/G ＜ 3 时，在靠近接收端处架索会发生很大的挠度变形，补给品垂向位置偏低，易发生事故。

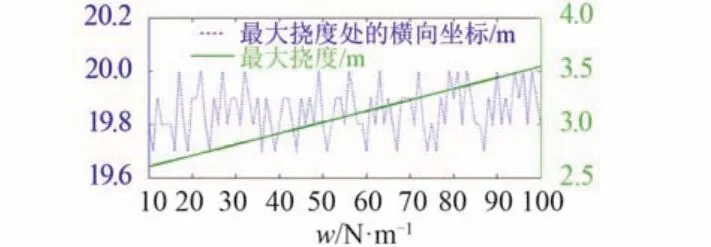
图8　不同架索自重时悬挂点最大挠度Fig. 8　Maximal deflection of suspension point when cable’s weight differs

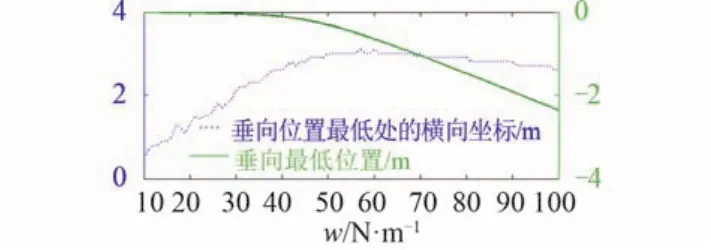
图9　不同架索自重时悬挂点最低位置Fig. 9　Lowest position of suspension point when cable’s weight differs

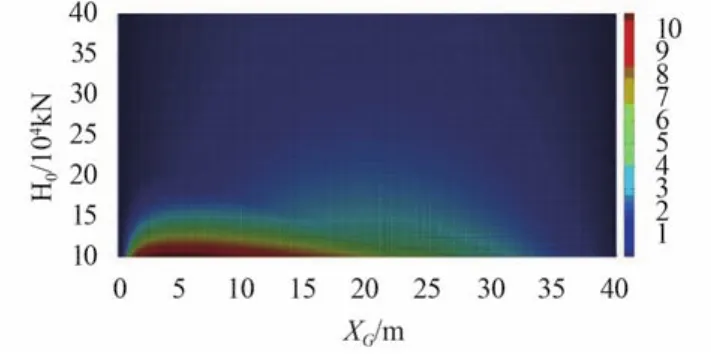
图10　不同水平张力时悬挂点挠度云图Fig. 10　Deflection nephogram of suspension point when horizontal tensile force differs

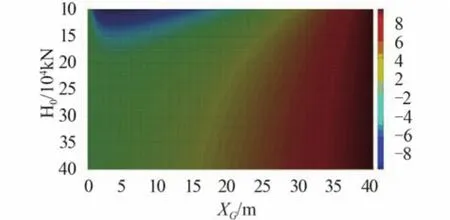
图11　不同水平张力时悬挂点挠度云图Fig. 11　Vertical position nephogram of suspension point when cable’s weight differs

图12 为水平拉力不同时架索挠度最大值及其对应的横向位置。当张力 H0/G ＜ 3 时，架索发生明显变形且挠度随着张力的增加缓慢减小；随着张力的进一步提高，架索挠度迅速减小并逐渐趋于稳定值，且其对应横向位置始终在补给端；当到达 H0= 20 kN 时候，架索挠度已经可以忽略不计。

图13 为水平拉力不同时架索垂向最低位置及其对应的横向位置。当张力 H0/G ＜ 4 时，架索最低位置低于接收点，补给品可能存在落水的危险。当 H0/G ＞ 4时，架索垂向最低位置趋于稳定，悬挂点在补给品输运过程中基本均位于水面以上，因此工程常取用 H0/G = 4[1]。在整个水平张力变化范围内，架索最低点对应的横向位置始终位于距接收点 0～4 m 范围内，且当 H0/G ＞ 4.5，接收点即为架索的最低点。

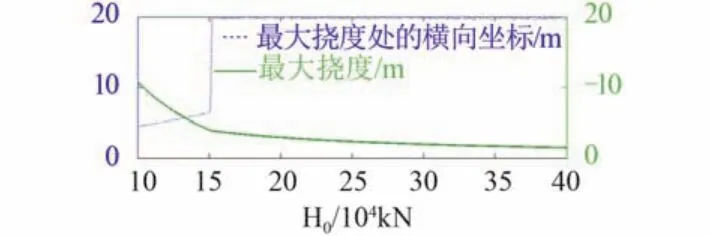
图12　不同水平张力时悬挂点最大挠度Fig. 12　Maximal deflection of suspension point when horizontal tensile force differs

图13　不同水平张力时悬挂点最低位置Fig. 13　Lowest position of suspension point when horizontal tensile force differs

3　结　语

本文从悬链线方程出发，建立了计入架索长度和自重变化的海上横向补给高架索系统静力学分析模型，并通过与文献数据的对比，验证了本文方法的可靠性和普适性。基于上述静力学方程，定量研究了架索单位长度质量和水平张力等参数对高架索线形的影响。

研究结果表明，高架索在输运过程中可能存在2种线形，架索单位长度质量和水平张力的变化会显著影响架索线形，其挠度最大处和垂向位置最低处并不一致。在保证架索张力的前提上应尽量减小单位长度质量，当水平张力与补给品重量比值大于 4 时，架索线形已经趋于稳定。

参考文献：

[1]严梅剑. 海上航行横向补给装置选型设计[J]. 船舶, 2004(1): 51–53.

[2]邓凯, 李红涛, 余建星. 高架索航行补给中船舶在波浪中的运动性能研究[J]. 船舶力学, 2009, 13(2): 217–225.

[3]赵小兵, 赵伟, 马良荔, 等. Ian航行横向补给高架索张力及张力波动控制参数仿真[J]. 舰船电子工程, 2007, 27(5): 115–117.

[4]何学军, 张良欣, 任爱娣. 海上横向补给系统高架索参数影响分析[J]. 海军工程大学学报, 2009, 21(5): 52–56, 66.

[5]马仁刚, 张良欣, 何学军. 横向干货补给系统高架索的静力学分析[J]. 舰船科学技术, 2012, 34(2): 47–49, 80.

[6]卢永锦. 海上横向补给高架索道系统数学模型研究[J]. 中国造船, 1996(1): 19–22.

[7]阎宏生, 余建星, 郭海涛. 海上轻型高架索补给系统的力学分析及安全性研究[J]. 海洋技术, 2006, 25(2): 39–43.

[8]余建星, 李红涛. 高架索海上补给装置在小型船舶补给上的应用[J]. 海洋技术, 2005, 24(2): 59–62.

[9]施平安, 何立居, 叶家玮. 两船波浪中并靠补给相对运动模型试验研究[J]. 船海工程, 2012, 41(5): 26–30.

Statics analysis of alongside-arranged highline cable replenishment system at sea based on catenary equation

GUO Fei, LI Jing-wei
(Marine Design &Research Institute of China, Shanghai 200011, China)

Abstract:Statics analysis model is established based on catenary equation for alongside-arranged highline cable replenishment system at sea after considering influence of cable’s length and weight. Effects of several parameters, including cable’s unit weight and tensile force, are then discussed. It is found when the ratio of horizontal tension to cargo weight exceeds 4, the deflection of highline cable is ignorable to safely transfer cargos.

Key words:replenishment at sea；highline cable；catenary equation；cable configuration analysis

作者简介：郭飞 (1989–)，男，硕士，助理工程师，主要从事船舶舾装设计。

收稿日期：2015–06–09； 修回日期: 2015–12–07

文章编号：1672–7619(2016)03–0037–04

doi：10.3404/j.issn.1672–7619.2016.03.008

中图分类号：U674.98

文献标识码：A