非线性Black-Scholes期权定价模型的数值模拟
2016-05-17陈迎姿王晚生
陈迎姿,王晚生
(长沙理工大学 数学与计算科学学院,长沙 410114)
非线性Black-Scholes期权定价模型的数值模拟
陈迎姿,王晚生
(长沙理工大学 数学与计算科学学院,长沙 410114)
摘 要:Black-Scholes期权定价方程是现代金融理论最大的成就之一,随着期权市场的快速发展,对期权定价理论的研究由线性转变为非线性.本文利用牛顿迭代法直接解由隐式Euler方法及有限差分法离散所得的非线性代数方程组.通过MATLAB编写相应的程序,并对不同网格下求得的数值解进行对比,结果表明该方法是无条件稳定的和收敛的.
关键词:Black-Scholes方程; 期权定价; 有限差分法; 牛顿迭代法; 隐式Euler方法
现代期权定价理论的最新革命始于1973年,美国芝加哥大学的教授Fisher Black和Myron Scholes[1],推导了基于不支付红利的股票的任何一种衍生证券的价格必须满足的一个微分方程,提出了著名的Black-Scholes期权定价公式,为投资者提供了适用于股票的任何衍生证券且计算方便的定价公式,并因此而获得了诺贝尔经济学奖.该模型的计算结果很好的反映了期权的公平市场价格和相应的风险,并且很好的解释了期权价格如何伴随标的资产价格的变化而变化[2,3].当考虑交易成本、市场流动性等因素时,Black-Scholes模型就由线性变为非线性模型.近年来,这些非线性模型特别受到关注[4,5].由于市场流动性是金融风险管理中受到高度关注的问题,在本文中,我们针对Frey和Patie[4]提出的非流动市场中的期权定价模型进行讨论.
这个期权定价模型已在文[6]中进行了详细分析,并构造了一种2阶的分裂算法求解空间离散后的线性化常微分方程组.我们将利用牛顿迭代法直接求解空间离散后的非线性常微分方程组.
1 有限差分离散
首先引入非线性Black-Scholes期权定价方程[4,6]:
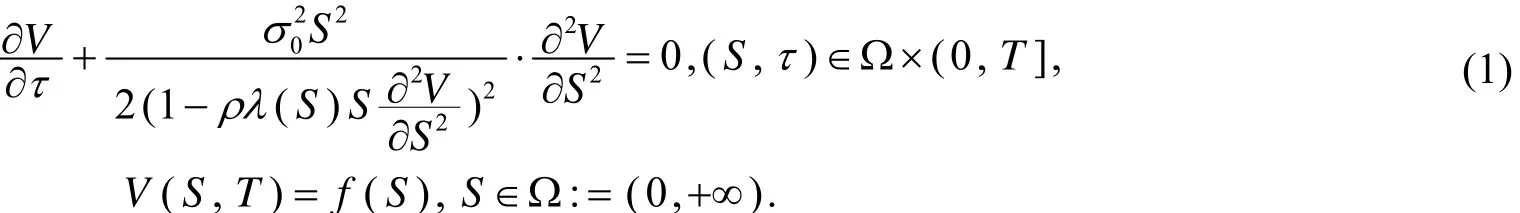
其中S表示标的资产的价格,T表示期权的截止日期,0σ表示资产的波动率,ρ表示衡量市场流动性的参数,连续函数λ(S)描述了市场的流动性状况,我们假定收益函数f(S)是一个连续的分段函数.
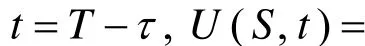

为了计算问题(1)的数值解,考虑有限的边界区域(S ,t)∈ [0,b ]×(0,T ],且满足Dirichlet边界条件:
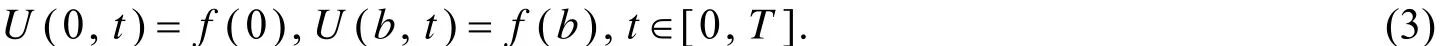
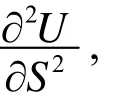
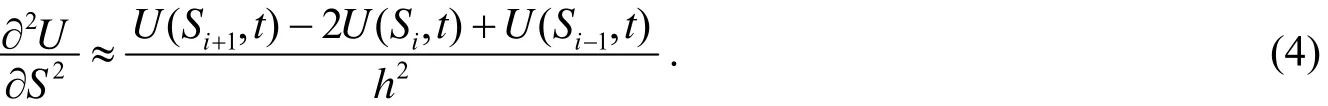
令Ui=U(Si,t),则方程(1)可化为
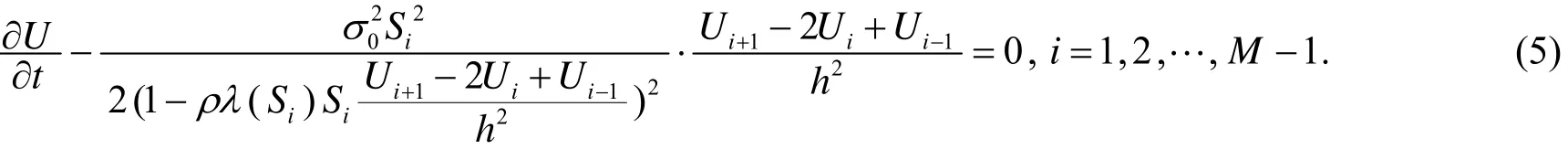
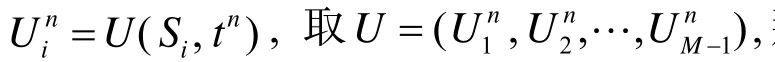
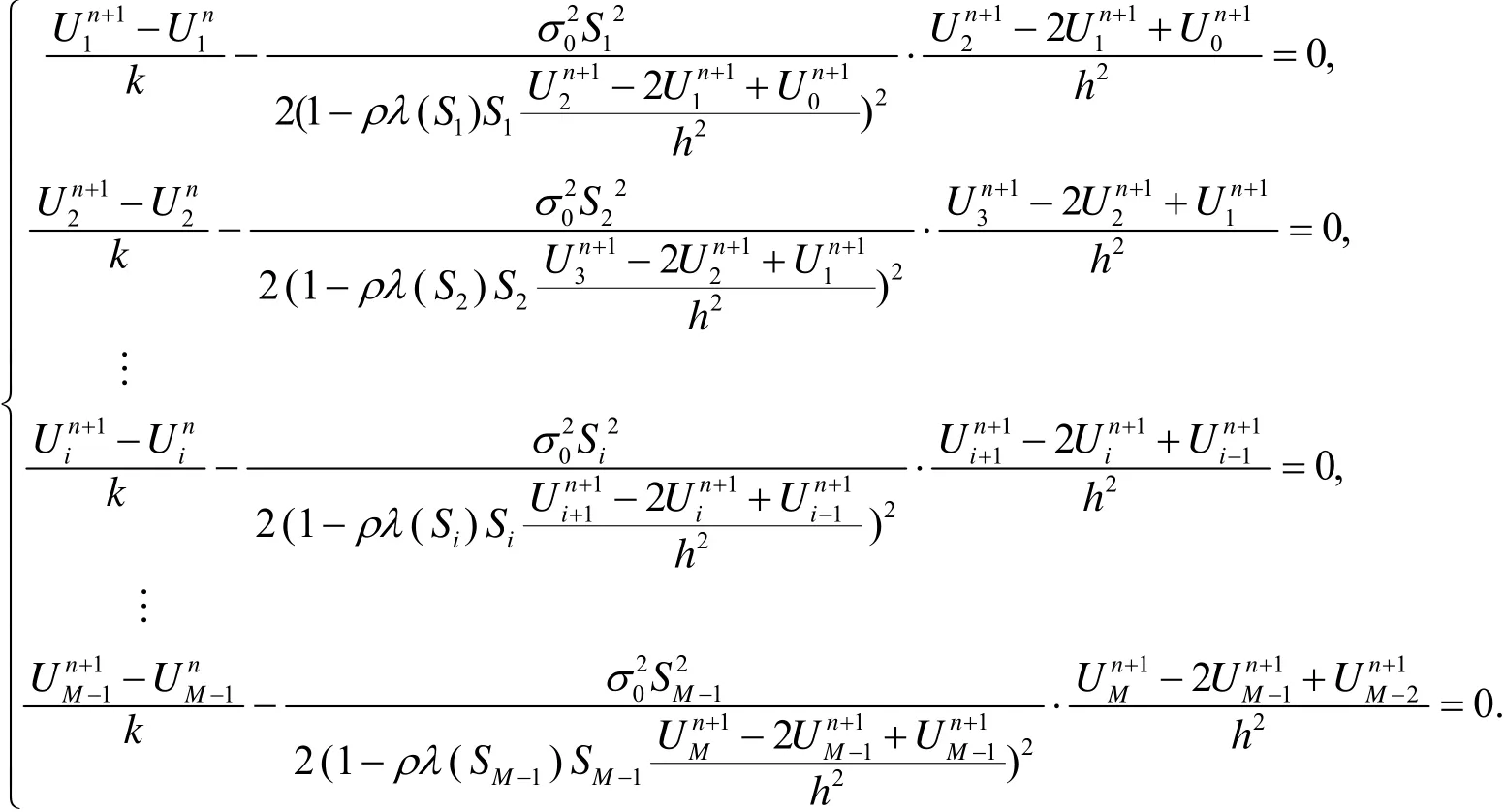
这是一个非线性方程组,采用牛顿迭代法解这个方程组,即
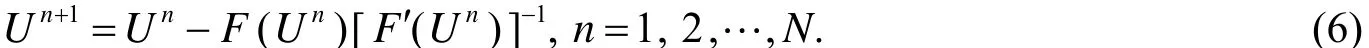
对Un求偏导,得到Jacobi系数矩阵
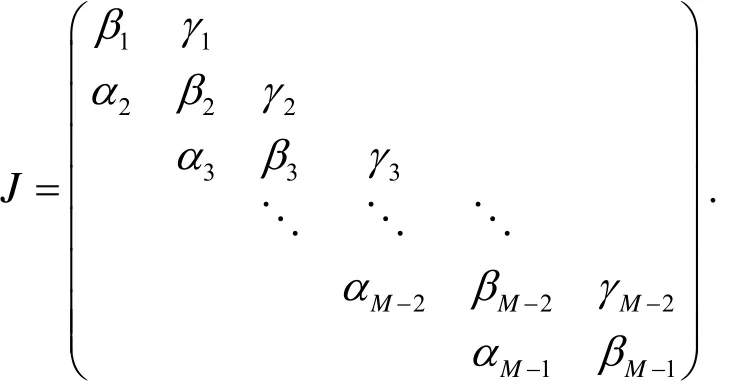
其中,当i =1时,

当i=2,…,M-2时,

当i=M-1时,
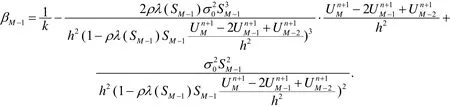
2 数值实验
为了说明该方法的有效性,我们给出欧式看涨期权的数值实验.假设λ(S)= 1 ,那么的市场价格的波动性就由ρ来确定.
例1 根据欧式看涨期权的特性,首先我们给定边界条件
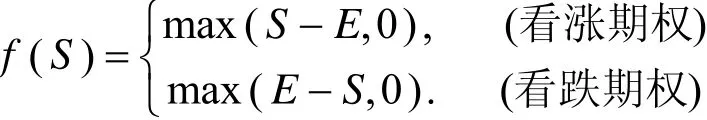
其中E表示执行价格,给定参数的取值,E =100 ,波动率σ0= 0.2 ,截止日期T =0.25,取边界区域b =200 .通过对粗网格和细网格的数值结果进行比较,采取无穷范数来描述两网格的相应点数值解的误差[6],即

下面给出具体的实验结果.


表1
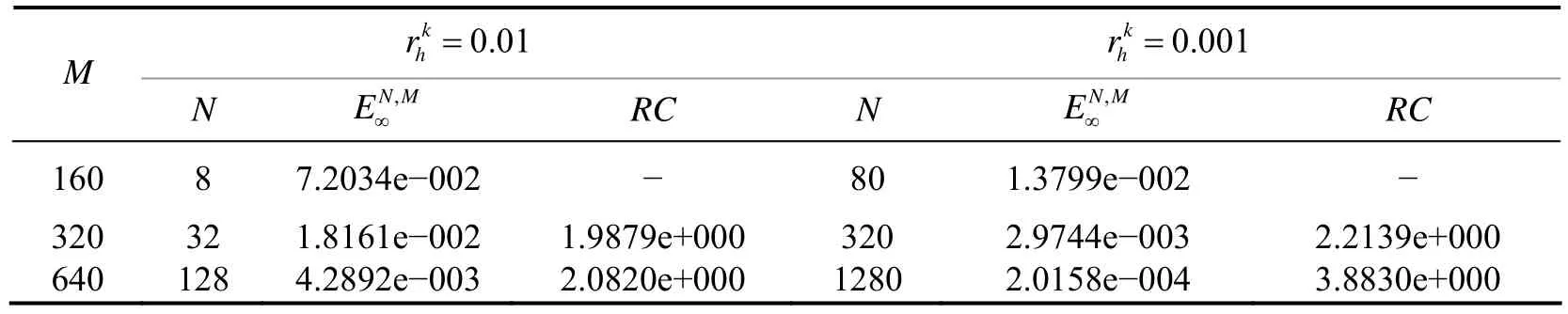
表2
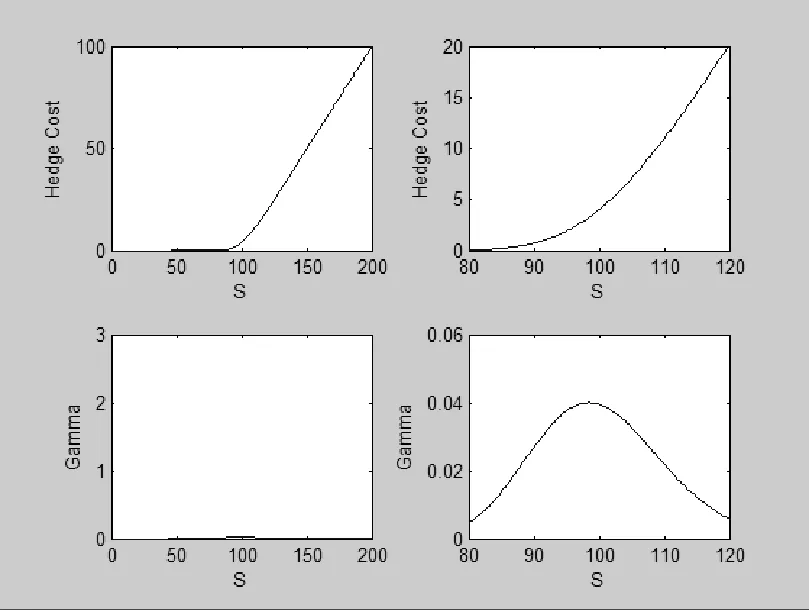
图1

图2
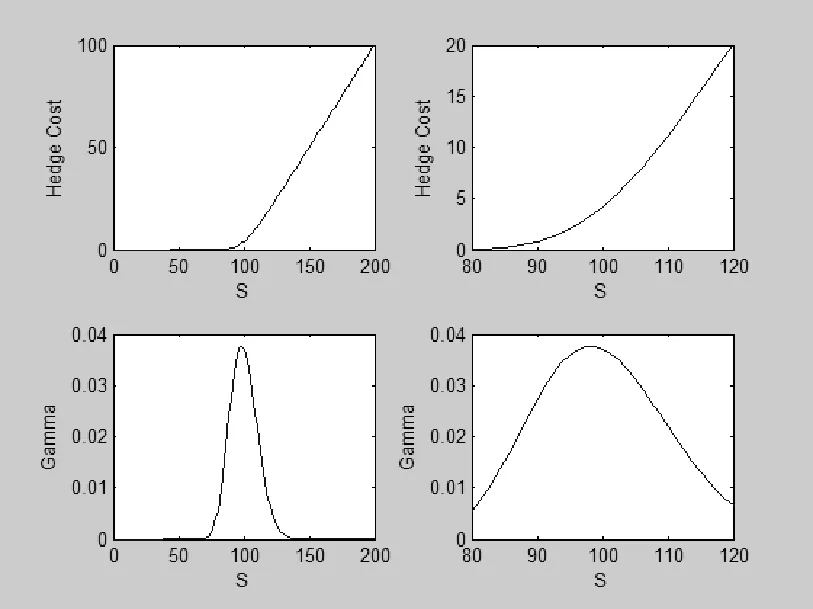
图3

图4
例2 考虑欧洲蝶式期权,此时
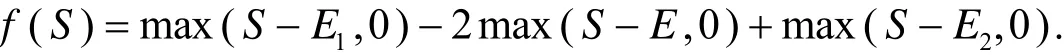
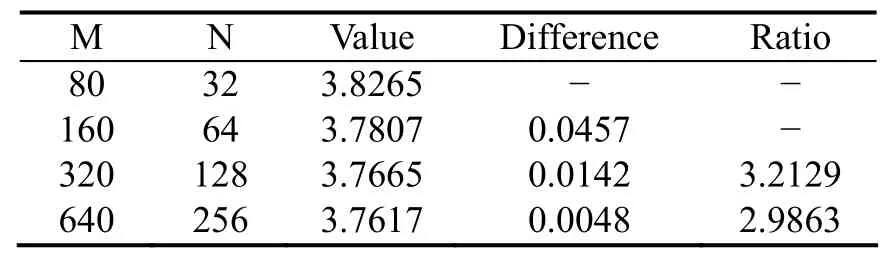
表3
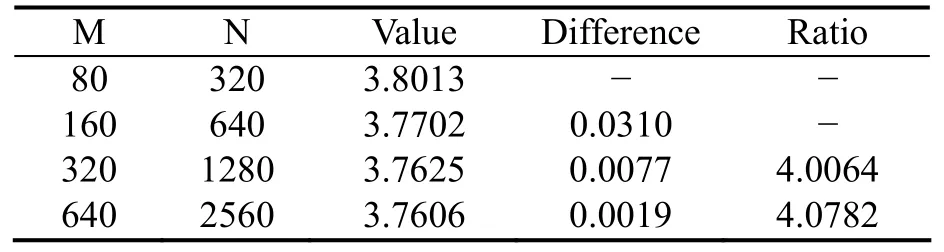
表4
图5、图6和图7分别给出了当N =1024时,不同ρ、M取值得到的期权定价格.图5给出了当取ρ=0.001 ,M =640 ,N =1024时的欧式看涨期权的价格和相应的Gamma函数图像; 图6给出了当取ρ=0.01 ,M =160 ,N =1024时的欧式看涨期权的价格和相应的Gamma函数图像; 图7给出了当取ρ=0.1 ,M =16 ,N =1024时的欧式看涨期权的价格和相应的Gamma函数图像.显然,本文所使用的方法是有效且可靠的.
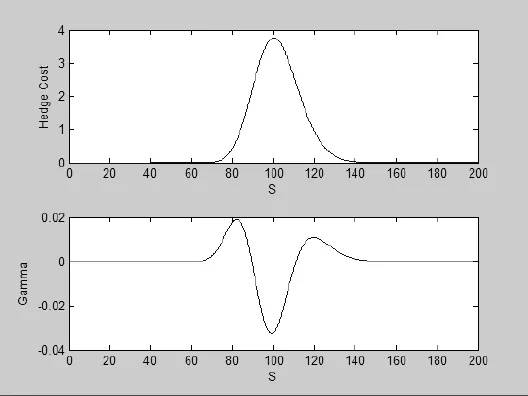
图5

图6

图7
参考文献
[1] Fisher Black,Myron Scholes.The Pricing of Options and Corporate Liabilities [J] .The Journal of Political Economy.1973,81(6): 133~155
[2] 姜礼尚.期权定价的数学模型和方法[M].第2版.北京: 高等教育出版社,2003: 74~109
[3] 姜礼尚.金融衍生产品定价的数学模型与案例分析[M].北京: 高等教育出版社,2008: 28~78
[4] R.Frey,P.Patie.Risk management for derivatives in illiquid markets: a simulation-study [C].in: K.Sandmann,P.Schönbucher(Eds.),Advances in Finance and Stochastics,Springer,Berlin,2002,pp.137~159
[5] Jianqiang Guo,Wansheng Wang.An unconditonally stable,positivity-preserving splitting scheme for nonlinear Black-Scholes equation with transaction costs [C].Sci.World J.2014,11.ID 525207
[6] Jianqiang Guo,Wansheng Wang.On the numerical solution of nonlinear option pricing equation in illiquid markets[J].Computers and Mathematics with Applications,2014: 117~133
Numerical Simulation of Nonlinear Black-Scholes Option Pricing Model
CHEN Ying-zi,WANG Wan-sheng
(School of Mathematics and Computational Science,Changsha University of Science and Technology,410114,Hunan,changsha)
Abstract:Black-Scholes option pricing equation is one of the biggest achievements in modern financial theory.With the rapid development of the options market,the study of the option pricing theory is changed from linear to nonlinear.We use Newton iterative method for the numerical solution to nonlinear equations derived from the option pricing equation by implicit Euler method and finite difference method.The numerical results confirm the unconditional stability and convergence of the method.
Key w ords:Black-Scholes equations,option pricing,finite difference methods,Newton iterative method,implicit Euler method
通讯作者:王晚生(1977−),男,湖南株洲人,长沙理工大学数学与计算科学学院教授.主要研究方向: 微分方程数值解
作者简介:陈迎姿(1989−),女,湖南永州人,长沙理工大学数学与计算科学学院硕士研究生.主要研究方向: 微分方程数值解
基金项目:国家自然科学基金项目(11371074); 湖南省自然科学基金项目(13JJ1020); 湖南省教育厅重点项目(13A108); 湖南省国际经济与国际工程管理研究中心基金项目(16IEPM06)
收稿日期:2015-12-20
中图分类号:O241.8
文献标识码:A
文章编号:1672-5298(2016)01-0012-05
