无格室钢-混结合段构造形式与受力性能分析

张　凯,刘永健,琚明杰,刘　江

(1.长安大学　公路学院，陕西　西安　710064；2.东莞市交通投资集团有限公司，广东　东莞　523010)



无格室钢-混结合段构造形式与受力性能分析

张凯1,刘永健1,琚明杰2,刘江1

(1.长安大学公路学院，陕西西安710064；2.东莞市交通投资集团有限公司，广东东莞523010)

摘要：为研究无格室钢-混结合段不同构造形式的受力性能，本文以梨川大桥无格室钢-混结合段为研究背景，通过数值分析方法分别就两种不同连接件构造形式的钢混结合段受力性能进行了分析。计算分析结果表明：钢-混结合段PBL和栓钉连接件顺桥向应力分布不均布，靠近承压板位置受力较大；负弯矩区结合段混凝土部分顶板横向应力分布不均匀，预应力筋的设置对其结合部位混凝土顶板应力横桥向分布有影响；钢梁顶底板的刚度过渡加劲肋和等高U肋的突变部分，具有较大局部应力集中；栓钉连接件和PBL与栓钉组合的连接件形式对结合段部位混凝土和钢顶板受力影响不大。

关键词：桥梁工程；钢-混结合段；数值模拟；受力性能；开孔钢板连接件

0引言

混合梁通过对两种材料的合理利用，在受力性能、跨越能力、经济性能等方面得到了很大改善，在桥梁建设中得到越来越多的应用[1]。钢-混结合段作为混合梁桥的一部分，其主要作用是将钢与混凝土两种材质的结构结合在一起，使两者之间刚度过渡平顺、传力合理，有效充分发挥混合梁桥中钢与混凝土两种材料各自的优势。混合梁桥钢-混结合段主要有“有格室”和“无格室”两种构造形式[2]。实际应用过程中，钢-混结合段的构造形式因桥型与跨径的不同而不同。结构方案(有无格室)与构造形式(主要是连接件形式)的选取是混合梁桥设计的关键。

近些年，国内一些学者[3-9]结合工程实例分别对重庆石板坡大桥、鄂东长江大桥、九江长江大桥等有格室钢-混结合段进行了理论与试验研究。国内针对无格室钢混结合段的研究相对较少，文武松等[10]以汕头礐石大桥为研究对象，设计了1∶2 倒梯形缩尺模型试件，分析了连接部位的受力及邻近区域的应力分布；陈开利[7]等针对舟山桃夭门大桥采用1∶2 的缩尺模型试验,研究了结合段在各种不利荷载作用下各部分共同工作的特点、力的传递途径及力的分布规律；胡建华、蒲怀仁等[8,11]针对佛山平胜大桥进行了1∶4缩尺模型试验和数值模拟，将开孔钢板连接件(PBL)应用于混合梁桥中，并对连接件进行了推出试验以研究其力学性能；吴文明、刘高等[12-13]通过简化节段局部模型对无格室钢混结合段进行了有限元参数分析和轴压传力分析，并推导出连接件剪力大小及分布的简化理论计算公式；刘玉擎等[14]针对结合段钢加劲过渡段进行了试验与解析分析。国外针对组合梁的研究较多，少部分单独针对结合段的研究中，Dunai[15]针对轴压及循环荷载作用下的钢-混结合段力学行为进行了数值与试验研究；Kim S.E.和Kim S.H.[16-18]等对工字型钢板梁与混凝土梁的拼接结合段进行了数值计算及大小两种比例的模型试验，对不同连接件形式与仿真计算等进行了研究。

现有无格室钢-混结合段的研究以缩尺模型试验为主并辅以数值分析，上述试验均以验证设计的合理性为目的。此外，现有研究均是针对设置栓钉连接件或PBL连接件的结合段，栓钉与PBL组合的连接件形式近些年在组合梁桥中发展迅速，其在无格室钢-混结合段中的研究还未见报道。

本文通过工程实例对无格室钢-混结合段各部分构造的受力性能进行了分析，并就两种不同连接件形式(栓钉连接件和栓钉与PBL组合连接件)的受力性能进行了对比，所得分析结论旨在为工程设计提供有益参考。

1工程背景

梨川大桥为无背索混合梁斜拉桥，跨径布置为(51.5+138+55)m，边跨为预应力混凝土梁，中跨部分梁段为预制拼装钢梁，近塔侧钢混结合段设置在距离塔根部24.5 m处，远塔侧钢-混结合段设置在距离边墩20.5 m处，总体布置如图1所示。结合段部位桥宽33 m，近塔和远塔侧钢-混结合段构造类似。梨川大桥钢-混结合段采用无格室承压传剪式构造，混凝土梁中的预应力钢束锚固在承压板上，并在承压板布置栓钉，方案一采用在顶底板布置栓钉与PBL的组合连接件的构造形式，如图2所示。本桥结合段承压板厚60 mm。栓钉直径为22 mm,长150 mm。PBL靠近承压板处高550 mm,端头处高400 mm,孔径为60 mm，内穿φ22钢筋。顶底板厚度均为20 mm。

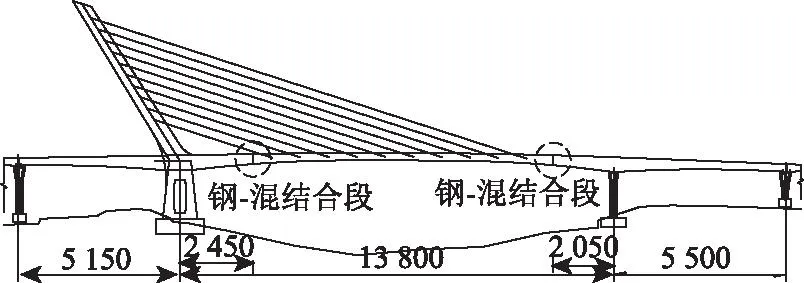
图1　梨川大桥总体布置图(单位：cm)Fig.1　General layout of Lichuan bridge(unit:cm)

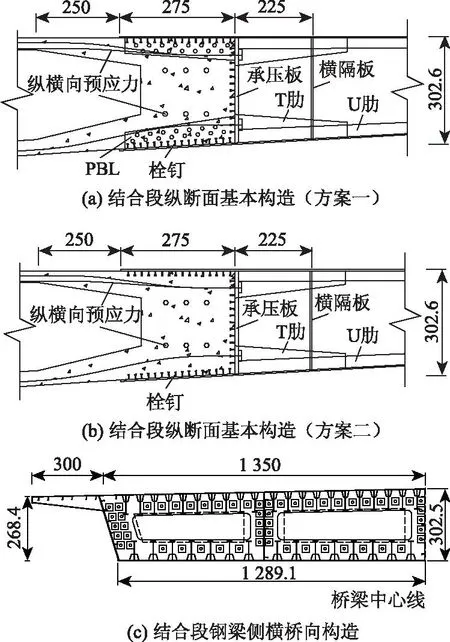
图2　梨川大桥钢-混结合段构造(单位：cm)Fig.2　Structures of steel-concrete connections in Lichuan bridge(unit:cm)

2模型建立

本文采用大型有限元软件ABAQUS对结合段进行数值模拟。

2.1材料属性与单元的选取

结合段钢梁、开孔钢板连接件(PBL)、栓钉等钢材均采用弹性本构模型。钢梁顶底板、承压板和PBL均采用实体单元C3D8R进行模拟。钢梁其他部分采用壳单元S4R模拟。考虑到栓钉数量较多，采用实体建模将使得模型网格划分质量难以保证，且严重影响计算效率，因此这里采用梁单元B32进行模拟。结合段混凝土采用弹性本构关系并采用实体单元C3D8R进行模拟。预应力筋采用桁架单元T3D2模拟。模型参数选取如表2所示。考虑到计算效率，普通钢筋与PBL孔内钢筋均未在模型中反映。

表2　模型材料参数表

2.2约束与接触的模拟

钢梁顶底板和承压板与混凝土之间的界面接触属性，切向为摩擦关系(摩擦系数为0.25)，界面法向为“硬”接触。栓钉、PBL及预应力筋均采用“埋入”功能处理，即将栓钉、PBL及预应力单元的节点自由度与埋入区域混凝土在合适位置自动建立约束关系。

2.3边界条件的模拟

根据圣维南原理，距结合部位较远区域的应力分布对结合段应力影响较小。在建模过程中，为了真实地反映实桥受力状态，各部件尺寸均按照实桥尺寸建模，并在原过渡段结束处再向两侧适当延伸以消除端部固结和耦合约束对结合段受力的影响。

预应力钢束按照实桥布置并张拉(计入预应力损失)，预应力的施加通过“初始应力”命令实现。计算模型中，在混凝土梁端采用固定约束，在钢梁端部施加内力组合。钢梁加载端部采用集中力加载，使用ABAQUS中的“耦合”功能将钢梁端面各节点的自由度耦合于端面中性轴上一点。加载内力通过整体杆系模型提取，选取杆系模型计算中最不利的正常使用极限状态短期荷载组合(1.0恒荷载+0.7汽车荷载+1.0人群荷载+1.0整体降温+0.8梯度升温)作为加载工况。梨川大桥远塔和近塔结合段构造类似但受力有所不同，这主要是由于斜拉索中巨大的索力对结合段受力有较大影响。限于篇幅，这里仅给出受力较为不利的远塔结合段的仿真计算过程。

2.4数值模型建立

针对梨川大桥钢-混结合段的构造特点，建立半宽横向对称模型，模型共531 820个单元，如图3所示。

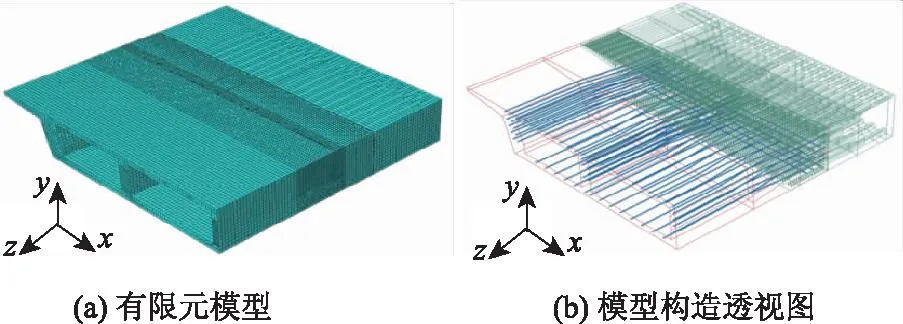
图3　结合段模型Fig.3　Model of steel-concrete connection

3受力性能分析

3.1连接件受力性能

梨川大桥钢-混结合段顶底板及承压板栓钉为等间距布置，顶底板栓钉顺桥向应力分布不均匀。通过有限元计算，提取轴力作用下的无格室顶板在顺桥向的各排栓钉根部剪力，将其传力情况绘于图4中，可以看出靠近承压板及远离承压板部位栓钉受力较大，中间部位受力较小。

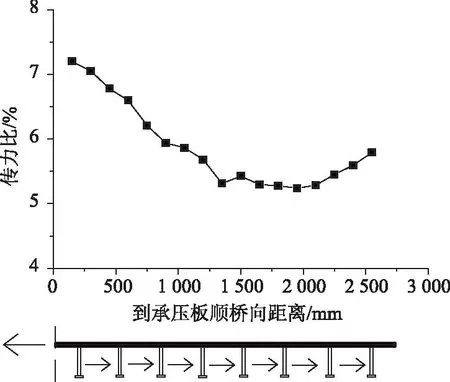
图4　顺桥向栓钉传力分配Fig.4　Longitudinal force distribution of studs

梨川大桥顶底板均布置顺桥向PBL连接件。顶底板PBL连接件受力有所不同，负弯矩作用下承压板顶部受拉，受拉传力主要靠预应力筋承担，顶板PBL对受拉传力有一定贡献；靠近承压板部位受力较大，远离承压板受力减小。对于底板PBL连接件，承压板底部传来的压力靠底板混凝土与PBL分担，底板PBL受力较大；顺桥向应力分布与顶板类似，远离承压板应力有所减小。顶底板von Mises应力与顺桥向应力变化曲线见图5和图6。

图5　结合段PBL连接件von Mises应力(单位：MPa)Fig.5　Von Mises stresses of PBL connectors in connection(unit:MPa)

图6　顶底板PBL von Mises受力顺桥向分布Fig.6　Longitudinal distributions of von Mises stresses of PBLs in top and bottom flanges

3.2混凝土梁段受力性能

钢-混结合段部位混凝土顺桥向应力如图7所示，由于悬臂部位未配置预应力束，顶板悬臂部分区域与顶板靠近承压板部位一定范围内有拉应力，其余部分均为压应力；模型计算中未考虑锚垫板的作用，预应力锚固部位压应力较大。

图7　钢-混结合段部位混凝土顺桥向应力(单位：MPa)Fig.7　Longitudinal stresses of concrete part in concrete-steel connection(unit:MPa)

选取具有代表性的两个截面，如图8所示，分别为钢混结合中间部位的A-A截面以及钢混结合结束部位的B-B截面，考察钢混结合部混凝土顶板正应力的横向分布规律。

图8　截面选取Fig.8　Selection of cross-sections

本桥钢-混结合段为单箱四室构造。以桥宽横向为横坐标(桥梁中线位置为零点)，截面顶部单元正应力为竖坐标，所选取的截面应力分布如图9所示。3个腹板中心的位置已在图中用竖线标记。通过分析，A-A与B-B截面应力分布比较类似，应力横向分布不均匀，腹板位置应力较其他部位低；两个截面的应力分布形式与普通箱梁横向分布规律类似，但负剪力滞效应明显。本桥悬臂部分未设预应力筋，悬臂部分区域具有拉应力。

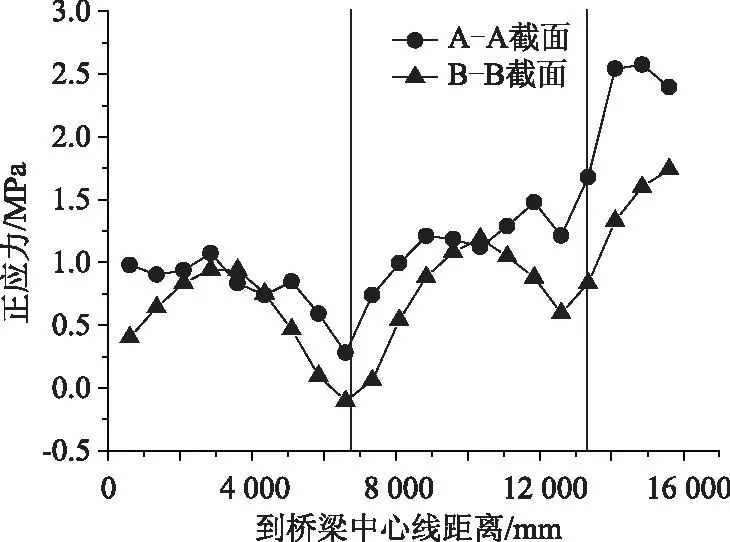
图9　截面顶板正应力横桥向分布Fig.9　Transverse distributions of normal stresses in top flange

在箱梁剪力滞效应分析中，剪力滞效应的大小通常引入剪力滞系数λ反映[19]：

(1)

式中，σ(x,y,z)为考虑剪力滞效应的截面一点(x,y,z)的纵向弯曲应力；σ0为按照材料力学初等梁理论计算获得的该点纵向弯曲应力。

针对A-A与B-B截面的负剪力滞情况，通过对比模型研究预应力效应对其的影响，对比结果如图10所示。

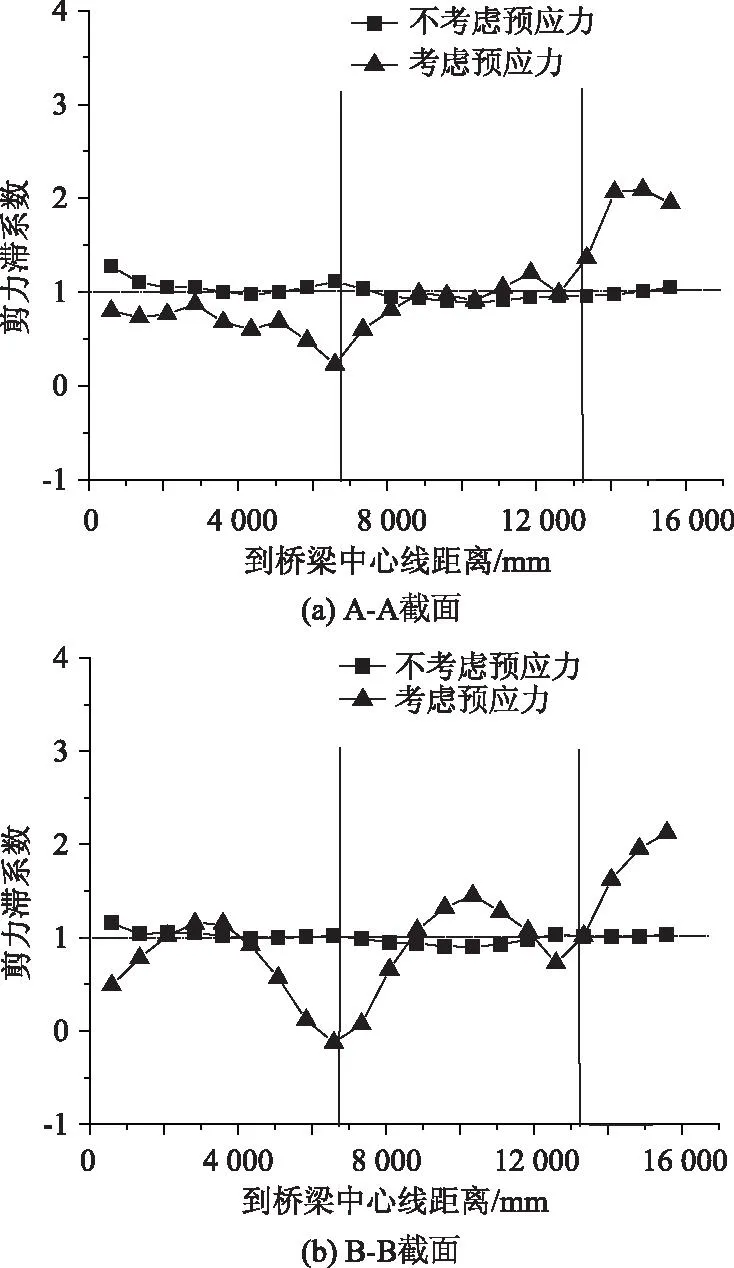
图10　A-A截面和B-B截面混凝土顶板剪力滞系数比较Fig.10　Comparison of shear lag coefficients of A-A and B-B sections in concrete top flange

对比分析可知，钢混结合部位混凝土顶板顺桥向应力横向分布不均匀，设置纵向预应力筋对其分布规律有影响。未设置预应力筋的横向分布剪力滞系数相对较为均匀，设置预应力筋后剪力滞系数变化较大。从图10可以看出，顶底板预应力筋横向布置不均匀，腹板束布置较多，横桥向剪切变形不均匀再加上腹板较大的预压应力，使得远离腹板位置压应力分配相对较少，顶板正剪力滞效应转变为负剪力滞效应。预应力筋的布置对结合部顶板应力横向分布有影响。

值得注意的是，边腹板以外的翼缘部分由于未设置预应力筋，其所受拉力较大，部分区域在使用过程中可能开裂。设计中针对该情况可在翼缘部分增设预应力筋或采用钢纤维混凝土等抗拉强度较大的混凝土填充。

3.3钢梁段受力性能

钢梁段von Mises应力分布如图11所示，钢-混结合段部位顶底板应力较钢梁部分小，这是由于结合段部位顶底板通过剪力连接件与混凝土协同受力的缘故。

钢梁段最大应力分布在顶底板的刚度过渡加劲肋和等高U肋的突变部分，即刚度突变处，本部分具有较大局部应力集中。

图11　钢梁段von Mises应力(单位：MPa)Fig.11　von Mises stresses of steel beam(unit:MPa)

4不同连接件构造形式对比分析

连接件的构造形式对结合段受力及传力性能均有影响。本部分针对图2中的两种不同连接件构造方案，对其受力性能进行对比分析。结合段连接件一般采用栓钉、PBL或栓钉与PBL组合的连接件形式，如图12所示。

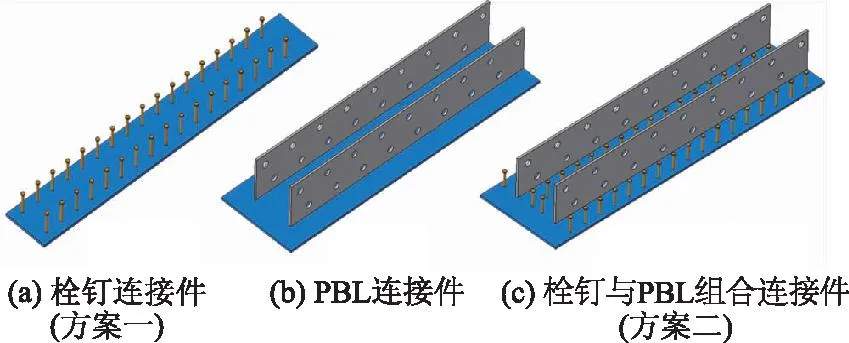
图12　结合段连接件构造形式示意Fig.12　Structural types of connector in steel-concrete connection

栓钉作为一种施工方便、质量容易保证的连接件，其应用较多，其力学性能不具方向性。栓钉连接件在无格室钢-混结合段中应用较多。PBL连接件在无格室钢-混结合段中的应用较栓钉少。与栓钉连接件不同，PBL的抗剪刚度具有方向性。PBL的优势在于较大的抗剪刚度与承载力，并可作为加劲肋来使用。

根据前文，靠近承压板部位连接件受力较大，因此选取如图8所示的A-A和B-B截面，分别对这两个截面的混凝土顶板正应力进行对比，如图13所示。分析可得：两种设计方案中，结合部位混凝土顶板正应力横桥向变化规律相一致；PBL与栓钉组合的连接件形式方案正应力稍小；两种设计方案所对应的连接件形式的不同对钢-混结合段顶板混凝土正应力影响不大。

图13　A-A截面和B-B截面混凝土顶板正应力比较Fig.13　Comparison of normal stresses of A-A and B-B sections in concrete top flange

为进一步分析连接件构造形式对结合部位钢顶板受力的影响，分别选取距离承压板顺桥向距离300 mm和600 mm的1-1截面和2-2截面，如图14所示。

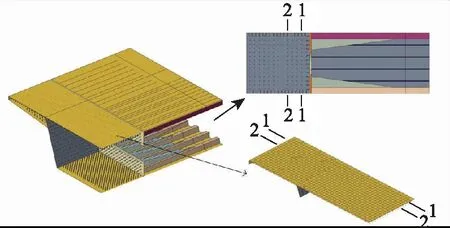
图14　选取截面示意Fig.14　Selection of cross-section

应力计算结果如图15所示，分析可得：靠近承压板的1-1截面和2-2截面，钢顶板von Mises应力横桥向分布规律一致，靠近腹板位置应力较大，正剪力滞效应明显；对比1-1截面和2-2截面，钢顶板von Mises应力随到承压板的距离增加而迅速减小，且应力横向变化幅度减弱；对比两个截面中不同连接件构造形式下钢顶板的受力可以看出，加设PBL的方案一所对应的钢顶板von Mises应力较方案二波动较大，靠近PBL与顶板连接处的部位应力较大，两个PBL之间的部位应力相对较小。方案一中，钢顶板应力的横桥向波动主要是由于PBL的影响。取方案一中的部分钢顶板von Mises应力横桥向分布绘于图16中，可以看出，其受力与箱梁的翼缘剪力滞效应类似，PBL的存在使得顶板横桥向剪切应变分布不均匀，靠近PBL与顶板相连接的部位应力较大。实际受力过程中，钢顶板应力横桥向分布较数值分析均匀，这主要是由于数值分析难以准确模拟PBL连接件中的混凝土榫和贯穿钢筋等。

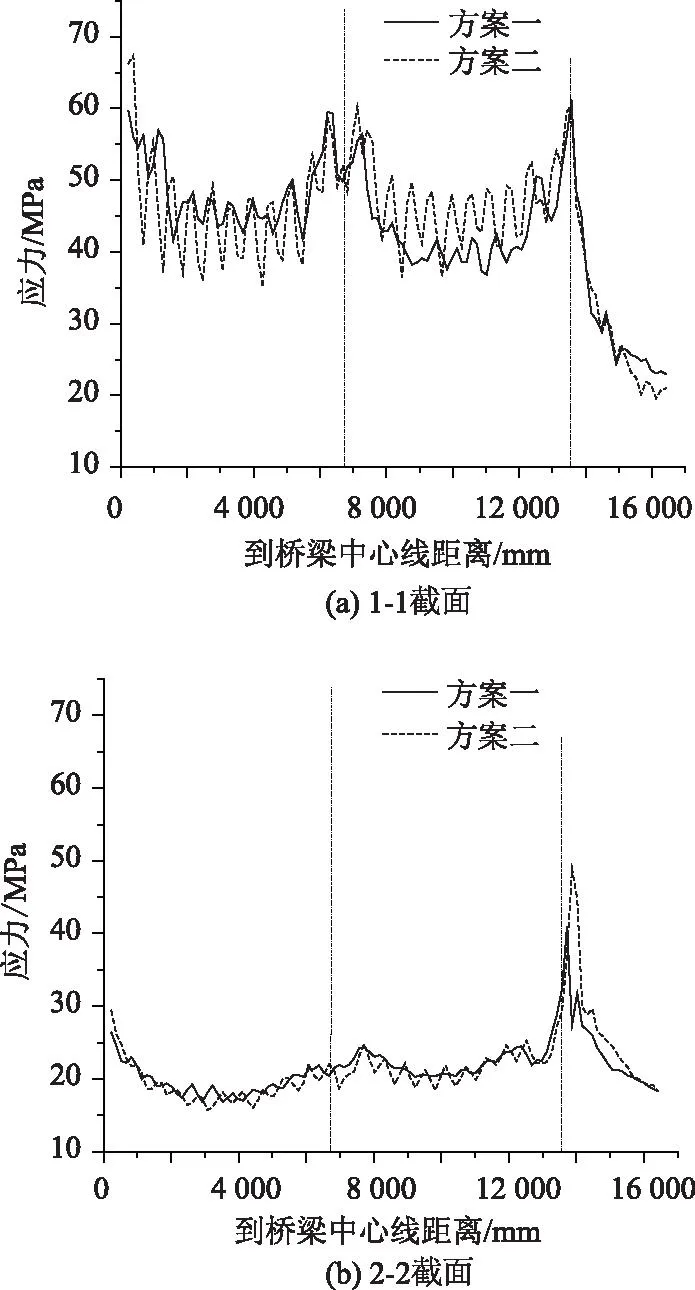
图15　1-1截面和2-2截面钢顶板应力比较Fig.15　Comparison of normal stresses of 1-1 and 2-2 sections in steel top flange

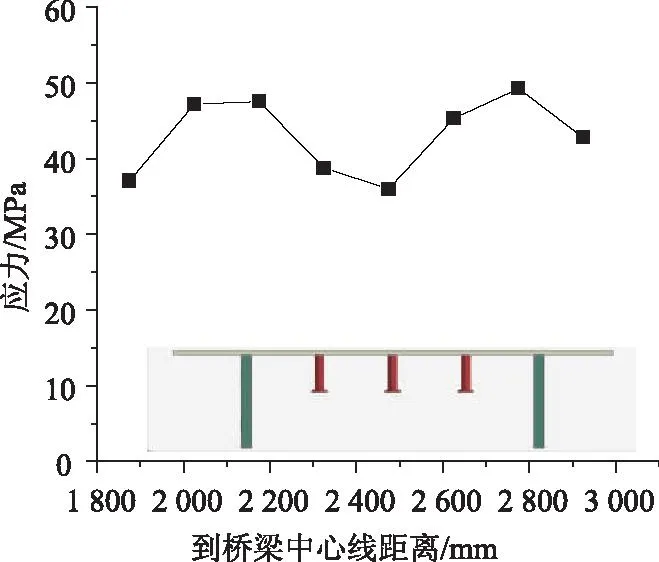
图16　钢顶板应力横桥向分布Fig.16　Transverse distribution of stresses of steel top flange

5结论

本文以梨川大桥为工程背景，对无格室钢-混结合段的构造形式及受力性能进行了分析。研究结论如下：

(1)无格室钢-混结合段PBL和栓钉连接件顺桥向应力分布不均布，靠近承压板位置应力较大，建议设计过程中优化连接件端部的设计。

(2)负弯矩区结合段混凝土部分顶板横桥向应力分布不均匀，预应力筋的设置对结合部位混凝土顶板应力横桥向分布有影响。针对悬臂部分拉应力，建议在该部分设置预应力筋或采用钢纤维混凝土等抗拉强度较大的混凝土填充。

(3)钢梁顶底板的刚度过渡加劲肋和等高U肋的突变部分，具有较大局部应力集中。

(4)栓钉连接件和PBL与栓钉组合的连接件形式对结合段部位混凝土和钢顶板受力影响不大。限于数值模拟的局限性，建议通过桥位实测对于无格室钢-混结合段两种构造形式的实际受力状况做进一步研究。

参考文献：

References:

[1]陈开利，余天庆，习刚. 混合梁斜拉桥的发展与展望[J]. 桥梁建设, 2005(2)：1-4.

CHEN Kai-li, YU Tian-qing, XI Gang. Development and Prospective of Hybrid Girder Cable-stayed Bridge [J]. Bridge Construction, 2005 (2): 1- 4.

[2]刘玉擎. 混合梁接合部设计技术的发展[J]. 世界桥梁，2005(4): 9-12.

LIU Yu-qing. Development of Design Technique for Joint Parts of Hybrid Girder[J]. World Bridge,2005(4):9-12.

[3]刘安双，刘雪山，代彤，等. 重庆石板坡长江大桥复线桥钢-混凝土接头设计[J]. 桥梁建设，2007(2): 35-38.

LIU An-shuang, LIU Xue-shan, DAI Tong, et al. Design of Steel and Concrete Joints of Double-Line Bridge of Shibanpo Changjiang River Bridge in Chongqing [J]. Bridge Construction,2007(2):35-38.

[4]刘明虎，徐国平，刘峰. 鄂东大桥混合梁钢-混凝土结合部研究与设计[J]. 公路交通科技，2010，27(12): 78-85.

LIU Ming-hu, XU Guo-ping, LIU Feng. Study and Design of Steel-concrete Joint Part of Hybrid Girder of Edong Bridge[J]. Journal of Highway and Transportation Research and Development, 2010，27(12)：78-85.

[5]张奇志，吴宝诗. 九江长江公路大桥钢-混结合段模型试验研究[J]. 桥梁建设, 2013,43 (5): 68-74.

ZHANG Qi-zhi, WU Bao-shi. Model Test Study of Steel and Concrete Joint Section of Jiujiang Changjiang River Highway Bridge[J]. Bridge Construction, 2013,43(5):68-74.

[6]刘承虞，赵廷衡. 礐石大桥钢梁与混凝土梁结合段设计[C]// 中国土木工程学会桥梁及结构工程学会第13 届年会论文集.上海: 中国土木工程学会桥梁及结构工程学会, 1998：304-308.

LIU Cheng-yu, ZHAO Ting-heng. Design of Steel-concrete Girder Joint Section of Queshi Bridge [C]// Proceedings of Thirteenth Annual Conference of Bridge and Structural Engineering Society of China Civil Engineering Society. Shanghai: Bridge and Structural Engineering Society of China Civil Engineering Society, 1998: 304-308.

[7]陈开利，王戒躁，安群慧. 舟山桃天门大桥钢与混凝土结合段模型试验研究[J]. 土木工程学报， 2006，39(3): 86-90.

CHEN Kai-li, WANG Jie-zao, AN Qun-hui. Model Tests on Steel-concrete Joining Section of Main Girder of a Cable-stayed Bridge [J]. China Civil Engineering Journal, 2006,39(3):86-90.

[8]蒲怀仁. 佛山平胜大桥钢混结合段设计[J]. 公路工程， 2011，36(3):90-94.

PU Huai-ren. Design of the Joint Part of Steel-concrete Mixed Girder Bridge of Pingsheng Bridge of Guangdong[J]. Highway Engineering, 2011，36(3):90-94.

[9]张国泉，戴少雄. 独塔斜拉桥钢混结合段应力分析[J]. 结构工程师，2007，23(3): 26-30.

ZHANG Guo-quan, DAI Shao-xiong. Stress Analysis of Steel-Concrete Combined Sections in a Cable Stayed Bridge with Single Tower[J]. Structural Engineers，2007,23(3): 26-30.

[10]文武松，汪双炎，王邦楣. 混合型斜拉桥连接部位的传力研究[J]. 桥梁建设， 1997(3):75-81.

WEN Wu-song, WANG Shuang-yan, WANG Bang-mei. Research on the Force Transmission at the Joint of Composite Cable Stayed Bridge[J]. Bridge Construction，1997(3): 75-81.

[11]胡建华，侯文崎，黄琼. 混合梁自锚式悬索桥钢混接合段结构形式的对比试验研究[J]. 铁道科学与工程学报, 2007, 4(5): 28-34.

HU Jian-hua, HOU Wen-qi, HUANG Qiong. Experimental Study of Different Structure Forms of Steel-concrete Joint Section of Hybrid Self-anchored Suspension Bridge[J].Journal of Railway Science and Engineering, 2007,4(5):28-34.

[12]张喜刚，吴文明，刘高. 无格室-承压板钢-混凝土结合部力学模型及简化计算方法[J]. 公路交通科技, 2013，31(10): 49-53.

ZHANG Xi-gang, WU Wen-ming, LIU Gao. Mechanical Model and Simplified Calculation Method of Steel-concrete Connection Joint with Full-connection Bearing-plates[J].Journal of Highway and Transportation Research and Development，2013,31(10):49-53.

[13]吴文明，刘高，徐国平，等. 无格室-承压板钢-混凝土结合部构造的结构特性[J]. 公路交通科技，2010，27(3): 75-80.

WU Wen-ming，LIU Gao, XU Guo-ping, et al. Structural Characteristics of Steel-concrete Connection Joint with Full-connection Bearing-plate Type[J]. Journal of Highway and Transportation Research and Development, 2010,27(3):75-80.

[14]XIN H, LIU Y, HE J, et al. Experimental and Analytical Study on Stiffened Steel Segment of Hybrid Structure[J]. Journal of Constructional Steel Research, 2014, 100(13): 237-258.

[15]DUNAI L, FUKUMOTO Y, OHTANI Y. Behaviour of Steel-to-concrete Connections under Combined Axial Force and Cyclic Bending[J]. Journal of Constructional Steel Research, 1996, 36(2): 121-147.

[16]KIM S H, LEE C G, AHN J H, et al. Experimental Study on Joint of Spliced Steel-PSC Hybrid Girder, Part I: Proposed Parallel-Perfobond-rib-type Joint[J]. Engineering Structures，2011, 33(8): 2382-2397.

[17]KIM S H, LEE C G, KIM S J, et al. Experimental Study on Joint of Spliced Steel-PSC Hybrid Girder, Part II: Full-scale Test of Spliced Hybrid I-girder[J]. Engineering Structures, 2011, 33(9): 2668-2682.

[18]KIM S E, NGUYEN H T. Finite Element Modeling and Analysis of a Hybrid Steel-PSC Beam Connection[J]. Engineering Structures,2010, 32(9): 2557-2569.

[19]郭金琼，房贞政，郑振. 箱型梁设计理论[M]. 北京: 人民交通出版社, 2008.

GUO Jin-qiong, FANG Zhen-zheng, ZHENG Zhen. Design Theory for Box Girder [M]. Beijing: China Communications Press, 2008.

Analysis of Structural Types and Mechanical Performance in Steel-concrete Connections without Cell

ZHANG Kai1, LIU Yong-jian1, JU Ming-jie2, LIU Jiang1

(1.School of Highway, Chang’an University, Xi’an Shaanxi 710064, China; 2.Dongguan Communications Investment Group Co., Ltd., Dongguan Guangdong 523010, China)

Abstract：In order to research the mechanical performance of different types of steel-concrete connection without cell, based on the steel-concrete connections without cell in Lichuan bridge, we analyzed the mechanical performance of 2 types of such connection through numerical analysis method. The analysis result shows that (1) the PBLs and the studs in the steel-concrete connections have non-uniform mechanical behaviors in the bridge direction, the PBLs and the studs near the bearing plate have a larger inner force; (2) the transverse stress distribution of top flange in the steel-concrete connections under hogging moment is non-uniform distributed, while the arrangement of prestressed tendons has an impact on the distribution of stress of top flange of the connections in transverse direction; (3) the mutation parts of stiffening ribs and constant U-ribs on top and bottom flanges of steel beam possess greater partial stress concentration; (4) there is little influence of the connection types of the PBLs and the studs on the stress of concrete and steel flange of the connection.

Key words：bridge engineering; steel-concrete connection; numerical simulation; mechanical performance; perfobond connector

中图分类号：U448.38

文献标识码：A

文章编号：1002-0268(2016)04-0073-07

doi:10.3969/j.issn.1002-0268.2016.04.012

作者简介：张凯(1990-)，男，安徽五河人，硕士研究生.(ismaelz@163.com)

基金项目：国家自然科学基金项目(51178051)；交通运输部西部交通建设科技项目(2013318812410)；东江梨川大桥科研课题研究项目(R-[2014]26-624)

收稿日期：2015-05-25