基于Fluent的桥面泄水口截留能力分析

周　晖

(湖州交通规划设计院， 浙江 湖州　313000)



基于Fluent的桥面泄水口截留能力分析

周晖

(湖州交通规划设计院， 浙江 湖州313000)

摘要：针对桥面连续坡段截留率的经验公式未考虑侧面流的实际情况，采用数值模拟方法计算不同形式泄水口的截留率，研究影响截留率的因素，并对连续坡段截留率公式进行修正，为泄水口形式的正确选择与布置提供理论依据。

关键词：数值模拟；泄水口；水力计算；截留率

桥梁是公路的重要组成部分，而桥面积水对行车安全影响很大，因此桥面排水系统设计至关重要。实际工程中，道路排水系统设计时按城市暴雨强度及面积进行设计，而桥面排水设计则是按相关规范选择泄水口尺寸及位置，对雨水设计流量与泄水口排水能力均未进行充分分析，致使一些桥面排水不畅或排水效果达不到排水要求，从而影响了行车安全及公路的管理运营。

桥面泄水口是桥面表面排水的终端，桥面雨水必须通过泄水口排出桥面。截留率的大小直接影响到坡段底部排水量的大小，因此有必要对泄水口的截留率进行综合性研究，为泄水口形式的正确选择与布置提供理论依据[1-2]。由于连续坡段截留率的经验公式并未考虑侧面流，因此本文用数值模拟方法来计算泄水口的截留率，研究影响截留率的因素。另外，还对桥面连续坡段截留率公式进行了修正，并将其与数值模拟结果进行了对比。

1经验公式

JTG/T D33—2012《公路排水设计规范》推荐的公路桥梁常见的泄水口为圆形或矩形。其中，圆形泄水口直径一般为15～20 cm；矩形泄水口宽度一般为20～30 cm，长度一般为30～40 cm；泄水口顶部应采用格删盖板，其顶面一般比周围桥面铺装低0.5～1 cm[3]。桥面边沟一般为潜三角形边沟，且边沟横坡度一般与道路横坡度相同[4]。桥面边沟示意如图1所示。

图1　桥面边沟示意

桥面泄水口的排水能力一般用连续坡段截留率E计算。E是泄水口在连续坡段的截留量与拦水带内总水流量的比值，其表达式为：

(1)

式中：Qi为被泄水口截取的拦水带内水量；Q为拦水带内总水流量。

未被泄水口拦下的剩余水量Q0则可以表示为：

(2)

在桥面连续坡段上，除了距离纵坡顶最近的泄水口仅有一次截留，其余泄水口均有多次截留，因此研究桥面连续坡段中间泄水口截留更能趋近现实。由于桥面泄水口会截取流经泄水口宽度范围内的水流，范围之外的水流则会沿纵坡继续下流，与下方桥面水流一同流向下一个泄水口，因此桥面连续坡段中间泄水口截留率E1为：

(3)

式中：b为雨水口宽度；T为边沟过水断面总宽度。

美国联邦公路局对泄水口的截留率进行了大量研究，其指出：拦水带内水流速度较低时，泄水口截取全部正面水流，且随着坡度增大，水流通过泄水口时会出现跃水和飞溅现象，这一现象的产生与通过泄水口的水流速度以及泄水口长度有关[5-6]。研究表明，当泄水口取0.5 m时，其跃水速度达到了2 m/s以上，此时桥面纵坡已达到0.06，因此大部分情况下，泄水口很难产生跃水现象[7]。泄水口产生跃水时的流速和长度的关系如图2所示。

正面流被泄水口截留比率Rf的计算公式为：

(4)

式中：V为拦水带内水流速度，m/s；V0为拦水带流速发生跃水时的流速；Ku为对研究结果进行回归所得系数，取0.295。

结合美国联邦公路局对泄水口截留率的修正，桥面连续坡段中间泄水口截留率公式为：

E=RfE1

(5)

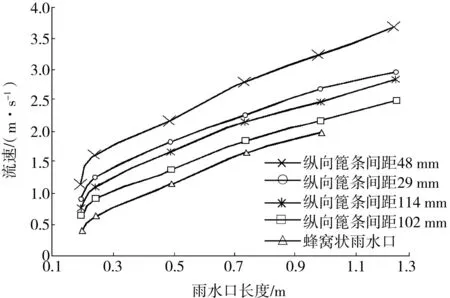
图2　泄水口发生跃水时流速和长度的关系

2Fluent数值模拟分析

2.1模型建立

Fluent是当前最流行的CFD软件之一，可用于流体、热传递和化学反应等方面模型分析。在降雨天气下，雨水在拦水带内的桥面流动，由于桥面的摩擦作用，积水呈现紊流运动状态，此时积水会出现波浪形的流线摆动，这种状态就是自由紊流状态[8]。本文数值模拟采用软件Fluent的RNG k-ε模型，以对不同形式泄水口排水进行计算，网格生成选用Fluent常用前处理软件Gambit。Fluent计算流程如图3所示。

图3　Fluent 计算流程

2.1.1网格划分

网格划分就是将计算区域进行离散，也就是把计算区域分成若干个子区域[8]。本次试验选用Gambit软件对模型进行划分，选用Fluent软件进行模型计算。计算模型结构采用四面体网格均匀划分，在泄水口处增加网格数量。Gambit生成的网格及Fluent计算网格如图4所示。

图4　桥面矩形泄水口网格示意

2.1.2边界条件

边界条件指在流体运动边界上控制方程应满足的条件，其通常会对数值计算产生重要影响。即使对同一个流场的求解，如果方法不同，则边界条件和初始条件的处理方法也不同[8]。本次模型计算设速度进口、压力出口、压力进口3类边界条件，如图5所示。

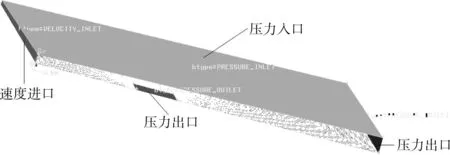
图5　模型边界条件设置

结合湖州市暴雨强度，确定模型进口速度为0.87 m/s，2级相的容积比率为1，表示按此速度进口的流体为水。为防止模型内部水出现回流现象，在模型上方设置压力入口，其工作单位为1个标准大气压，其值为101.3 kPa。模型有2个出口，一个是桥面泄水口的水流量流动出口，其排水方向垂直向下；另一个是拦水带内经泄水口后剩余水流量的出口，其方向为x方向。壁面边界条件用于限制流体和固体区域。桥面表面以及拦水带均为固壁边界，且是非滑移边界条件。模型材料为沥青混凝土，其粗糙系数为0.013[3]。

2.1.3计算区域及计算条件

2.1.3.1计算区域选择

模型中桥面泄水口选用矩形、圆形，泄水口排水面积大小按JTG D60—2004《公路桥涵设计通用规范》选择：对于高速公路和1级公路，一般采用直径为15 cm的排水管，间距在4～5 m之间。为研究过水断面宽度对泄水口截留率的影响，模型对y值从1～3 m每隔0.5 m进行选择，并建立了不同的计算区域。最终模型泄水口间距定为5 m，模型总长为7.5 m，宽为3 m，高为15 cm。

2.1.3.2计算条件

模型计算时，除了对解算器、模型、数值解法等进行设定外，还应对重力加速度及工作压力进行设置，并采用标准大气压。重力加速度的方向一般为竖直向下，本模型则为z轴的负方向，其大小为9.81 m/s2。

2.1.4计算结果

根据上述条件，计算长度2、5 m时泄水口水流情况，结果如图6所示。

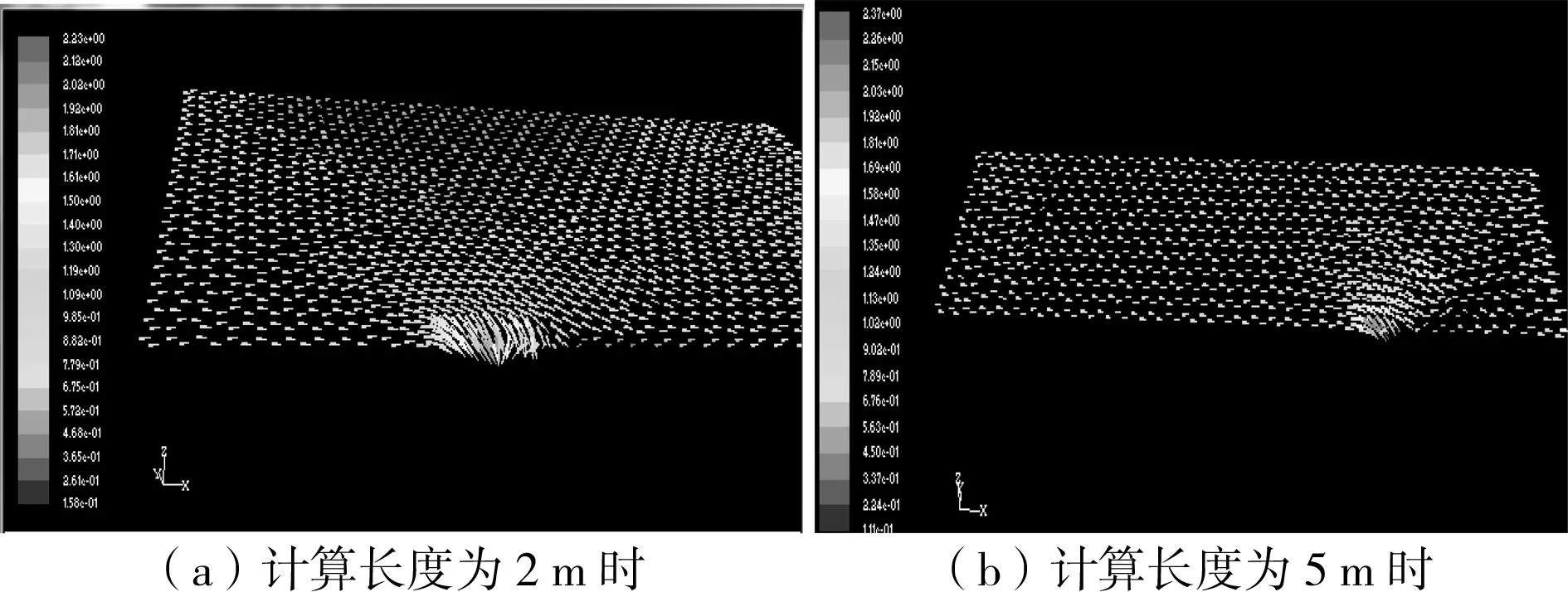
图6　泄水口水流情况

2.2截留率影响因素分析

桥面泄水口设计时，只有当连续下坡段泄水口的截留率计算合理且准确，才能更合理地布设泄水口间距，确保坡段底部或凹形竖曲线底部水量不大且能够及时排出，不至于因积水影响行车安全。部分截留率计算结果如表1所示。

出现上述现象是因为纵坡影响了泄水口附近的水流速度。对泄水口前段水流速度进行监控，输出结果如表2所示。从表2数据可知，当纵坡坡度为0.005时，水流速度为0.55 m/s，泄水口无论正面还是侧面都可以将水截留。在纵坡坡度为0.07时，水流速度为2.06 m/s，很容易发生跃水现象，致使截留率减小幅度增大。

2.2.1纵坡对截留率的影响

以横坡为0.02、过水断面宽2.5 m建立模型，研究纵坡对截留率的影响。纵坡坡度对截留率影响如图7所示。

1) 从图7可以看出：截留率随纵坡坡度增大而减小。

2) 截留率的变化有3个阶段，对于20 cm×40 cm矩形泄水口而言，当纵坡坡度从0.005增至0.03时，其截留率减少了15.15%；当纵坡坡度从0.03增至0.06时，其截留率减仅减少了3.03%；但纵坡从0.06增至0.08时，其截留率减少幅度又增加到7.28%。由此可知，纵坡对截留率的影响并不是单一的。

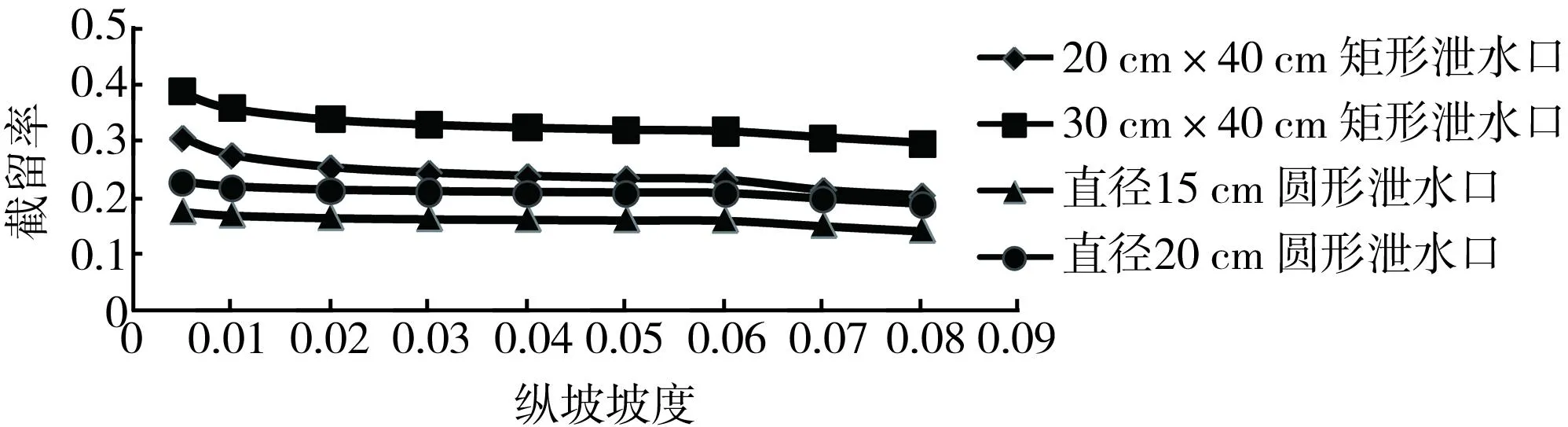
图7　纵坡坡度与截留率关系

2.2.2横坡对截留率的影响

为研究横坡对截留率的影响，以设计径流量Qs

表1　部分截留率计算结果

表2　水流速度随纵坡坡度变化

为0.07 m3/s，过水断面宽度为2.5 m，纵坡坡度为0.02固定不变建立数值模型。不同泄水口截留率输出结果如表3所示。

分析表3可知，随着横坡坡度增加，泄水口截留率逐渐增大。以20 cm×40 cm矩形泄水口为例，横坡坡度从0.02增至0.07时，其截留率增大了95.7%(接近1倍)。因此，进行桥面线形设计时，应在满足行车要求的前提下尽量增大横坡坡度，以便能更好地将拦水带内的水及时排出。

2.2.3泄水口形式对截留率的影响

为研究不同形式泄水口对截留率的影响，以设计径流量Qs为0.07 m3/s，过水断面宽度为2.5 m，纵坡及横坡坡度均为0.02固定不变建立数值模型。对泄水口前段水流速度的监测表明，水流速度为 1.1 m/s，模型水流速度小于2 m/s，不会产生跃水现象。不同泄水口截留率输出结果如表4所示。

对于矩形泄水口而言，有宽度和长度2个指标。从表4数据可知，随着宽度及长度增大，泄水口截留率也增大。当长度为40 cm，宽度从20 cm增至30 cm时，泄水口截留率增大了33.92%；当宽度为30 cm不变，长度从30 cm增至40 cm，泄水口截留率仅仅增大了3.76%。由此可知，矩形泄水口宽度对其截留率的影响要大于长度。

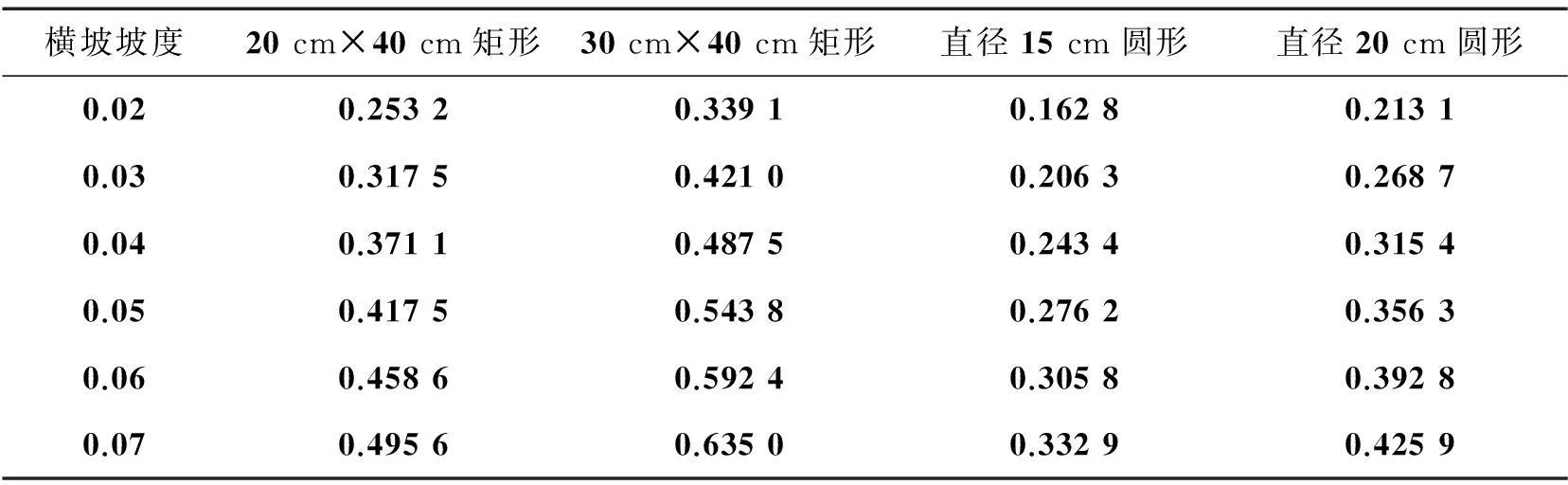
表3　不同横坡坡度下各泄水口的截留率

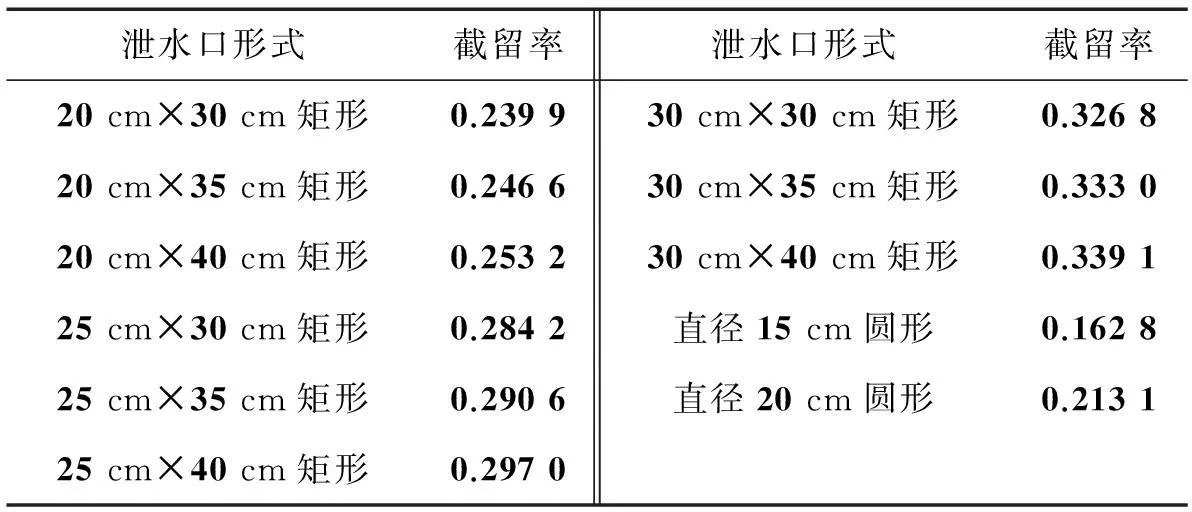
表4　不同横坡坡度下各泄水口的截留率

对于圆形泄水口而言，其截留率随着直径增大而增大，且圆形泄水口的截留率一般要小于矩形泄水口。

因此，选择桥面泄水口形式时，在不影响行车安全前提的情况下，应尽量增大泄水口的宽度，长度则选择一个较为合适的尺寸即可，没必要过度追求。同时，考虑篦子对矩形泄水口的影响，建议桥面矩形泄水口长度至少为40 cm，以防止产生跃水现象。由于矩形泄水口篦子容易堵塞，公路桥梁泄水口往往选择圆形，当选择圆形泄水口时，在不影响行车安全前提的情况下，建议选择直径20 cm的圆形泄水口。

3连续坡段截留率经验公式修正

泄水口排出的水流量分为2部分：正面水流和侧面水流。现用经验公式仅考虑了泄水口正面水流量，未考虑侧面水流量。所以，须对经验公式进行修正，使其计算结果更接近于实际水流[9]。

3.1总水流量

采用曼宁公式可计算拦水带内总的水流量：

(6)

式中：A为过水断面面积；C为谢才系数；R为水力半径；i为水力梯度；n为路面粗糙系数；i1为路面横坡；Sl为路面纵坡；h为拦水带内水深。

对于浅三角形拦水带而言，当公路表面水的宽度可能会超过水面深度40倍以上时，式(6)的水力半径便不能准确描述边沟形式。因此，采用修正过的曼宁公式进行流量计算，即在曼宁流速系数上乘以1.2的系数，则可得到规范中推荐的浅三角形拦水带流量计算公式[10-11]：

(7)

3.2侧面水流量

采用开口式泄水口理论分析侧面水流量，即堰流。侧面排水量计算公式如下：

(8)

式中：Qc为侧面排水量；m为堰流系数；g为重力加速度；hp为泄水口前水流平均水深；Lc为桥面泄水口长度。

3.3修正公式推导

排出全部侧面流量所需泄水口长度Lt的计算公式为：

(9)

联立式(8)、式(9)，得到如下Lt计算公式：

(10)

由于堰流并不能准确描述桥面泄水口的水流状态，因此，美国华盛顿运输部研究部门经过分析，确定系数K3=0.817[12]。同时将单一横坡拦水带泄水口长度Lt计算公式修正为：

(11)

泄水口外侧截流率可用如下公式表示：

(12)

整个桥面泄水口的截留率可以修正为：

E=RfE1+Ec(1-E1)

(13)

圆形泄水口截取侧面流的长度与矩形不同。由于圆形泄水口背对水流的半圆且不截取侧面流，因此可将圆形泄水口截取侧面流的长度修正为直径的一半，从而采用上述截留率修正公式对圆形泄水口的截留率进行计算。

4经验公式、修正经验公式、数值模拟对比

取横坡坡度及纵坡坡度均为0.02固定不变，设计径流量为0.07 m3/s，过水断面宽度为2.5 m，对采用经验公式、修正经验公式及数值模拟3种方式计算的截留率进行对比，结果如表5所示。从表5数据可知，修正经验公式计算的截留率大于经验公式计算的截留率，小于数值模拟计算的截留率，但与数值模拟计算的截留率非常接近。

表5　经验公式、修正经验公式与数值模拟的对比

5结束语

本文利用Fluent软件对不同形式泄水口排水能力进行了分析，并分析了不同纵坡、横坡及泄水口尺寸对截留率的影响，对泄水口尺寸及形式的选择提出了建议。

另外，考虑侧面流情况，本文引入开口式排水口理论，对泄水口连续坡段截留率的经验公式进行了修正，并将计算结果与数值模拟计算结果进行对比。结果表明，修正经验公式更接近于现实桥面排水情况，可用于工程实践中。

参 考 文 献

[1]张卓.竖曲线内桥面排水设计[J].长安大学学报(自然科学版)，2004，24(2)：45-47.

[2]姚宇，宰国军，严青苗.基于环保设计理念的桥梁排水设计[J].现代交通技术，2011，8(1)：32-35.

[3]中交路桥技术有限公司.JTG/T D33—2012公路排水设计规范[S].北京：人民交通出版社，2013.

[4]李志勇.路表排水计算理论与设计方案的研究[D].上海：同济大学，2006

[5]周维锋，李志勇.道路组合式排水口排水能力分析[J].交通标准化，2012(22)：42-45.

[6]于沉.公路路面宽浅边沟排水方式的探讨[J].东北公路，1997(2)：31-34.

[7]U. S. Department of Transportation Federal Highway Administration Offices of Research and78Development Implementation Division．Design of Urban Highway Drainage[M]．Washington，D.C.：[s.n.]，1979.

[8]于晓宇.微流控芯片上相变阀的研究[D].大连：大连理工大学，2009.

[9]沈波.路面排水街沟缘石平底开洞入水口截水量的计算[J].华东公路，1995(1)：29-31.

[10]杜群乐.公路路表排水口能力的计算方法[J].交通世界(建养机械)，2008(15)：93-95.

[11]李志勇，梅迎军.道路路表排水的截留率计算[J].重庆交通学院学报，2006，26(2)：67-71.

[12]RJCHARBENEAU，JJEONG，MEBARRETT .Highway Drainage at Superelevation Transitions[R].[S.l.]：Center for Transportation ResearchThe University of Texas at Austin，2008.

Analysis for Interception Capacity of Drain Openings on Deck Based on fluent

ZHOU Hui

Abstract:In allusion to the fact that the side flow is not considered in empirical formulae for interception rate of continuous slope sections on deck, this paper calculates the interception rates of drain openings in different forms by means of the numerical simulation method, studies the factors influencing the interception rates, and modifies formulae for the interception rates of continuous slope sections to provide a theoretical basis for correct selection and arrangement of drain opening forms.

Keywords:numerical simulation; drain opening; hydraulic calculation; interception rate

文章编号：1009-6477(2016)02-0057-06

中图分类号：U443.31

文献标识码：A

作者简介：周晖(1980-)，男，四川省遂宁市人，本科，高工。

收稿日期：2015-06-26

DOI:10.13607/j.cnki.gljt.2016.02.013