特殊铰接中心支撑框架结构振动台试验

张文元,麦　浩,于海丰

(1.结构工程灾变与控制教育部重点试验室(哈尔滨工业大学),150090 哈尔滨；2.哈尔滨工业大学 土木工程学院,150090 哈尔滨；3.河北科技大学 建筑学院，050018 石家庄)



特殊铰接中心支撑框架结构振动台试验

张文元1,2,麦浩1,2,于海丰3

(1.结构工程灾变与控制教育部重点试验室(哈尔滨工业大学),150090 哈尔滨；2.哈尔滨工业大学 土木工程学院,150090 哈尔滨；3.河北科技大学 建筑学院，050018 石家庄)

摘要:为研究铰接中心支撑框架结构体系的抗震性能和支撑体系的破坏模式，获得梁、柱中附加弯矩的变化规律，以8度抗震设防的某3层中心支撑框架结构为原型，按1∶4的缩尺比例设计制作试验模型，并对其进行了24种地震动工况的模拟振动台试验.发现在3种地震波(Coalinga-03、Kobe、Kocaeli)的多遇烈度以及人工地震波的罕遇烈度下，结构模型的层间位移角都满足中国现行规范要求.结构能够实现大震不倒，甚至在多次罕遇地震作用后仍然具有一定的安全储备，表明该体系在高烈度区也具有良好的抗震性能.支撑节点板的存在，导致梁柱上存在附加弯矩，特别是支撑失稳后附加弯矩的影响尤为明显.经历了多次罕遇地震动的检验，支撑及其连接的设计完全实现了强节点、弱构件的抗震原则.

关键词:特殊中心支撑框架结构；振动台试验；破坏模式；附加弯矩；抗震性能

特殊中心支撑钢框架体系相对于框架支撑双重体系而言，节点设计、加工和安装更加简单方便.特殊中心支撑由于杆件长细比适当放宽、并严格限制板件宽厚比，相对于普通中心支撑而言，其滞回环的饱满性和累积耗能能力都有所提高[1]，只要设计合理，该体系在高烈度区也具有良好的抗震性能[2].但中国的钢结构设计规范[3]和抗震规范[4]中都没有特殊中心支撑框架结构的设计条款.《建筑工程抗震性态设计通则》[5]仅给出了特殊中心支撑框架结构在不同抗震设计类别时的最大适用高度.国内对这种结构的抗震性能尚没有系统、深入的研究，没有形成统一的认识.

支撑与梁、柱采用节点板连接，不但传力明确，构造简单，而且更加接近于两端铰接、以受轴力为主的情况[6-8].但随层间变形的增加，支撑与梁柱连接的节点板仍会为梁端提供一定的转动约束.且节点板尺寸越大，梁端的转动刚度越大，在梁柱节点处产生的附加弯矩也越大.尤其是当支撑受压发生较严重的平面外失稳破坏、楼层蜕变为纯框架之后，梁柱上附加弯矩的效果更为明显[9].另外，已有研究结果[1]指出节点板上的支撑端部净距、支撑长细比和支撑翼缘宽厚比是影响支撑系统破坏模式的关键因素，并依据节点与支撑的先后破坏顺序，给出了支撑节点板的抗震设计方法，但仍有待在结构体系的实际地震响应中检验.为得到结构体系的地震反应特性并检验构件、节点等构造措施的合理性，研究节点板附近梁、柱上附加弯矩的变化规律，验证支撑伸入节点板的净距对支撑与节点板破坏顺序的影响，十分有必要对其进行模拟地震作用的振动台试验研究.

1试验模型设计

按照中国现行抗震规范[4]的振型分解反应谱法确定结构的地震作用，设计了两榀三层单跨具有拉链柱的人字形中心支撑框架结构，见图1、2.依据美国的AISC[10]中有关中心支撑框架的设计方法对梁、柱、支撑等重要构件进行设计.建筑所在场地的抗震设防烈度为8度，设计基本加速度为0.2 g，水平地震影响系数最大值为0.16，III类场地土，设计地震分组为第二组.梁腹板与柱翼缘通过抗剪板形成近似铰接连接；支撑与框架采用节点板连接，支撑伸入节点板的净距由支撑的长细比和宽厚比确定[1].根据试验场地条件限制和相似原则，当尺寸相似比取1∶4，质量相似比取1∶43.04时的效果较好.各主要物理量的相似关系见表1.

振动台试验模型的设计、制作及加载严格按照相似理论进行.楼面配重采用10 mm厚的钢板，每层重2 355 kg.试验模型的所有钢材均采用Q235B，钢材材性试验结果见表2.梁、柱分别采用H78×78×3.75×3.75、H78×65×3.75×3.75焊接工字形截面.根据各层支撑的长细比和截面宽厚比，设计了两种支撑端部伸入节点板的净距(2t、0t)，节点板与支撑构件的尺寸见表3、4.其中1、2层支撑端部净距为2t，第3层支撑为0t(t为节点板厚度).所有的支撑节点均保证连接的极限承载力大于连接件的全截面屈服承载力与钢材连接系数(1.25)的乘积.在施加配重板后，再将拉链柱现场焊接，确保其不承担竖向荷载.使用两榀完全相同的支撑框架结构作为试验对象，两榀之间设置侧向柱间支撑和铰接次梁，使其能够相互支撑，维持平面外的刚度和稳定性，形成完整的空间结构.次梁承担楼面配重，截面为 H78×70×6×6.使用高强螺栓将柱脚底板与底梁铰接.

表1　模型相似关系

表2　所用板件材性试验结果

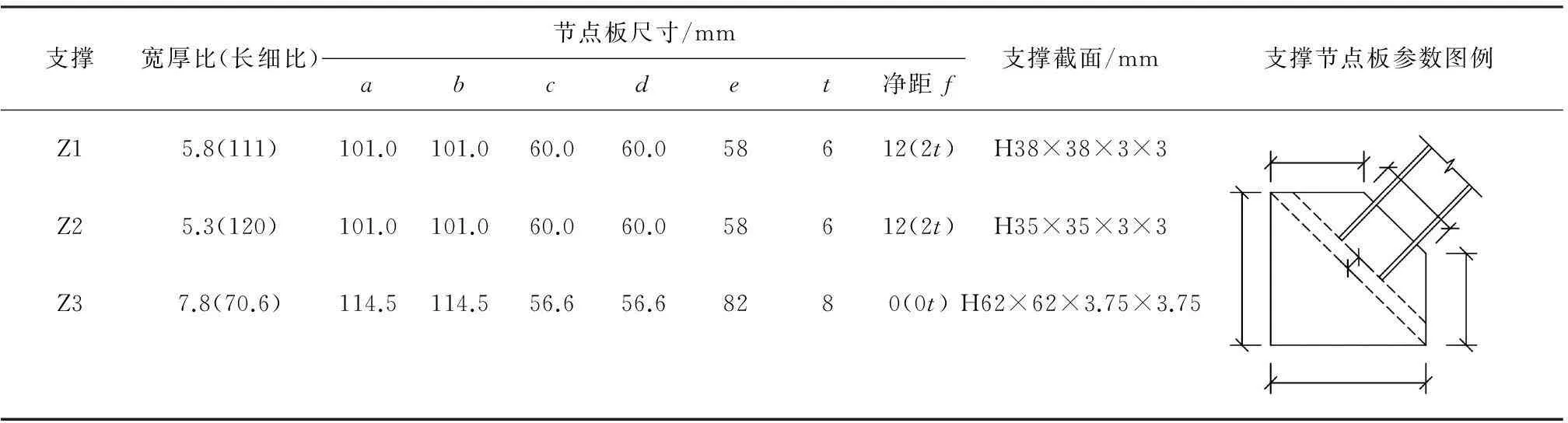
表3　支撑与梁柱连接节点板参数和支撑参数

注：Z1(2、3)依次为1、2、3层支撑.

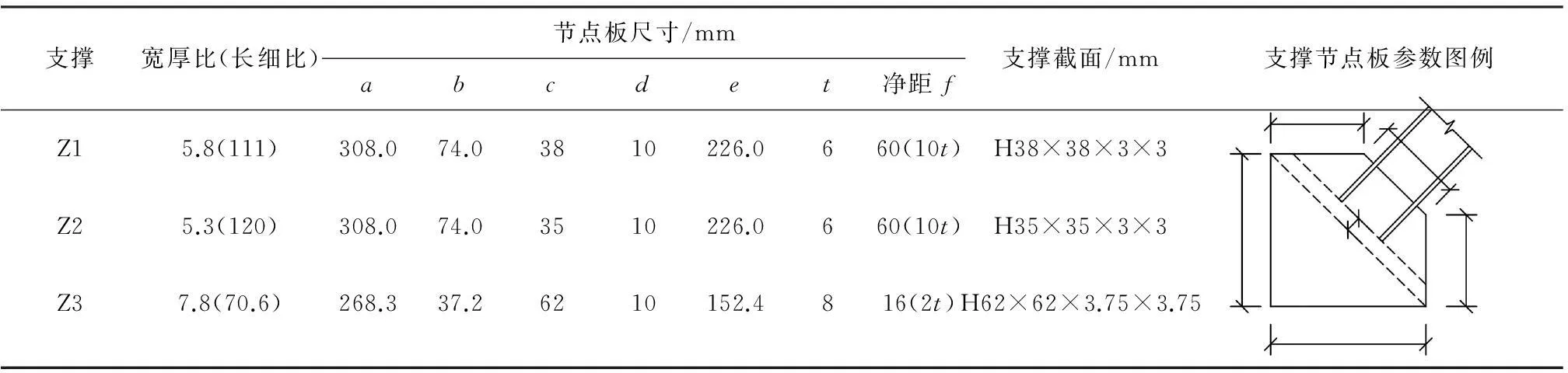
表4　支撑与横梁连接节点板参数和支撑参数

注：Z1(2、3)依次为1、2、3层支撑.

2实验方案

2.1传感器布置

本试验采用8个LVDT高精度位移计测量各层及底梁的水平位移，对称布置、每榀4个.使用7个拉线式位移计测量支撑及拉链柱的轴向变形，以观察支撑的失稳情况.加速度传感器7个，1个布置在振动台台面上，其余6个对称布置在各层标高处.在支撑端部的节点板上、节点板与梁柱连接处、支撑靠近端部4分点处、以及底层柱等关键部位上布置了124个应变测点.试验模型就位后见图1，传感器及应变测点的布置见图2、3.

图1　试验模型就位图

图2　一榀支撑框架及其传感器布置(mm)

图3　应变片测点布置

2.2加载步骤

根据地震动的频谱特性、有效峰值、地震动持时这三要素选择了8度多遇地震波4种，其中有3条天然波 Coalinga-03(Coa)、Kobe(Ko)、Kocaeli(Kt)以及一条人工波(Sy)，4种波的时程曲线见图4所示.而8度基本和9度罕遇地震波由人工波(Sy)调幅得到.本试验按照8度多遇、8度基本、9度罕遇、强震多波连续作用的顺序进行加载.试验中，加速度幅值和记录的时间间隔根据相似关系进行调整，其加速度和位移反应谱见图5、6.各加载阶段结束后，均对模型结构进行白噪声扫频，测量模型在不同试验阶段动力特性的变化.由于振动台存在系统误差，导致再现值与期望值存在一定差别，因此在8度多遇烈度(理论输入峰值188.3 gal)和8度基本烈度(理论输入峰值538.0 gal)的试验过程中需要对输入的加速度幅值进行调整，每条地震波输入两次.在进行8度多遇烈度振动台试验时，台面依次输入地震波Coa、Ko、Kt、Sy(对应工况Coa-1、Coa-2、Ko-1、Ko-2、Kt-1、Kt-1、Sy-1、Sy-2).8度基本烈度对应工况Sy-3、Sy-4.9度罕遇地震波(理论输入峰值1 668.0 gal)对应工况Sy-5.强震多波连续加载分4次进行，第1、2次为3个波连续加载，理论输入峰值为1.33×1 668.0 gal，对应工况Sy-6、Sy-7；第3次为3个波连续加载，理论输入峰值为1.41×1 668.0 gal，对应工况Sy-8；第4次为5个波连续加载，理论输入峰值为1.41×1 668.0 gal，对应工况Sy-9.本次振动台试验共进行包括白噪声扫频在内的24个工况.

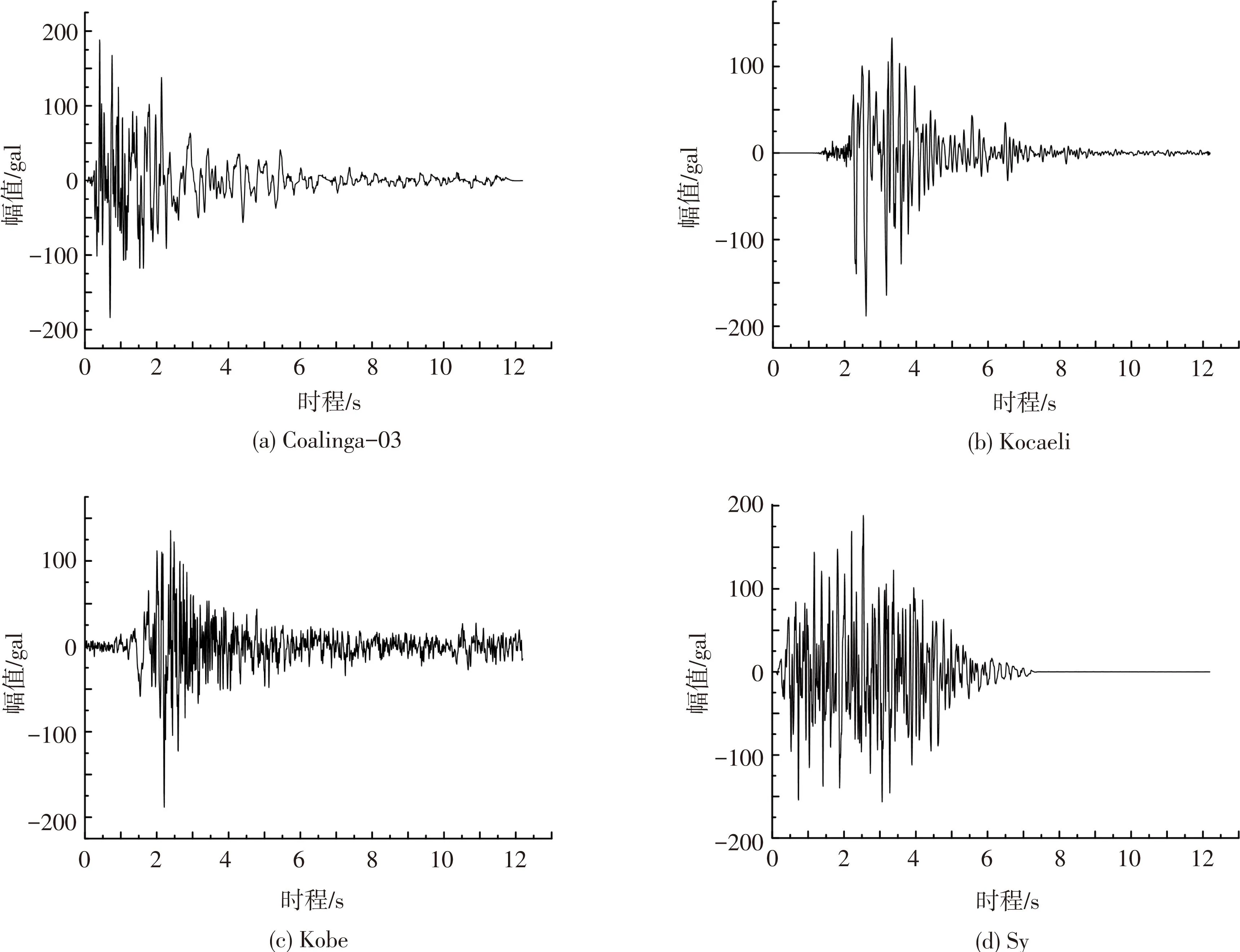
图4　所选加速度时程曲线

图5　加速度反应谱

图6　位移反应谱

3试验现象

在8度多遇、基本烈度地震动作用下，模型中的梁、柱、支撑等主要构件均没有观察到失稳或者其他不可恢复性的破坏，测得柱中最大轴压比为0.12.表明试验模型在8度基本地震动作用时，结构基本没有进入塑性.在9度罕遇地震动作用时，模型的反应明显比前两个阶段要剧烈，也能观察到在地震过程中支撑产生了很大的面外失稳变形，但地震结束后支撑大部分的面外变形得以恢复，结构整体的残余塑性变形不明显，表明结构仍有一定的抗倒塌能力和剩余的安全储备，可以进行更大荷载的试验.

多波连续强烈地震动作用下，模型的反应非常剧烈.地震动输入结束后检查发现，模型产生了较大的不可恢复性的塑性变形.第1、2层支撑发生了很大的平面外失稳，节点板出现了平面外的转动，底层支撑最大平面外残余变形达到34.3 mm，第2层支撑最大平面外残余变形为7.96 mm.但是梁、柱均没有明显变形，按拉链柱顶层桁架设计的第3层支撑均未发生面外失稳，满足设计初衷.测得柱最大轴压比为0.22.满足2t净距的1、2层节点板在强震下绕着塑性铰线转动，没有发生开裂破坏现象.从整体上看，结构仍然可以承受一定的荷载作用和具有一定的安全储备，结构仍能维持“大震不倒”.支撑平面外失稳和节点板平面外弯曲破坏现象见图7.

图7　试验结束后试件照片

4试验结果

对白噪声扫频得到的加速度响应和位移响应进行频谱分析，可以判断各试验阶段前后模型动力特性的变化，进而了解模型的工作状态.在8度多遇、基本烈度地震动前后，模型的第一、二阶自振频率没有变化，第一阶为8.16 Hz，第二阶为19.18 Hz；第一阶阻尼比为0.012，第二阶为0.029，说明模型在这些工况作用下依然处于弹性状态.在9度罕遇地震作用后，试验模型的第一阶自振频降为7.89 Hz，第二阶自振频率减小为18.98 Hz；第一阶阻尼比为0.028，第二阶为0.039，说明有部分抗侧力杆件发生了塑性变形、产生损伤所致.而连续多次强震输入后，白噪声扫频的第一阶自振频率已经降为6.97 Hz，第二阶自振频率减小到16.48 Hz；第一阶阻尼比为0.048，第二阶为0.055，说明试验模型的大部分抗侧力杆件已经产生了塑性变形，发生了很大的不可恢复性损伤.

4.1加速度响应

通过对各层加速度数据的处理可以得到各工况下楼层的加速度放大系数K，即该楼层加速度峰值与台面加速度峰值的比值.如果结构某一楼层发生了塑性变形，则该楼层的加速度放大系数相对于弹性阶段会有明显的减小.图8为不同工况下的每层加速度放大系数，括号内为台面输出加速度幅值，单位是gal.显然，模型在8度多遇地震以及基本地震作用时，各楼层的加速度放大系数随着楼层的增加基本呈线性增大，说明在8度多遇和8度基本地震动作用下，各层刚度没有降低，模型没有发生明显的损伤，依然处于弹性状态.而在9度罕遇地震作用后，各层的加速度放大系数发生了明显的变化，模型上部的加速度放大系数接近或小于1.0，说明模型已经产生一定程度的损伤，刚度有所下降，有抗侧力构件进入塑性，对地震波放大作用减缓.

4.2位移响应

图9为试验模型各层层间位移包络值曲线以及各层间位移角包络图，括号内为台面输出加速度幅值，单位是gal.可以看出，层间位移最大值发生在底层，为结构的最薄弱部位.在多波连续强震作用时，底层位移出现急剧增大的趋势，说明底层支撑已经发生了很大的平面外失稳破坏.8度多遇地震动作用时模型底层最大层间位移角为1/1 142，第2层最大层间位移角为1/1 194，顶层最大层间位移角为1/1 852，均满足现行抗震规范1/300的要求.9度罕遇地震动作用时试验模型底层位移角为1/284，满足现行抗震规范1/50的要求.即便是多波连续强烈地震作用时，底层层间位移角最大也仅为1/90.5.通过与数值计算得到的弹性层间位移角1/628.3相对比，可以发现在强震下此支撑框架具有较大的弹塑性变形能力.

图8　各楼层加速度放大系数

4.3梁柱附加弯矩

在模型设计时，梁柱节点按铰接构造，但是由于节点板的存在，使得梁柱的连接方式不再是理想铰接，而是呈现出半刚接特性.因此地震作用使楼层产生一定层间变形时，节点板与梁柱之间会产生相互作用力，使梁柱端部产生附加弯矩，附加弯矩最大部位通常位于节点板最外边缘处的梁柱截面上[9].可以通过分析此处梁柱翼缘、腹板的应变数据，算出弯曲应力，再根据截面特性转换成附加弯矩.本文给出人工地震波9度罕遇地震动时，底层柱和梁的附加弯矩时程曲线，以及最大附加弯矩与层间位移的关系.见图10.纵坐标为无量纲化的附加弯矩β=M/Mp的包络值，其中M为梁柱中的附加弯矩，Mp为梁柱的塑性铰弯矩.梁、柱上各种工况下的附加弯矩见表5.

图9　层间正向位移及层间位移角包络图

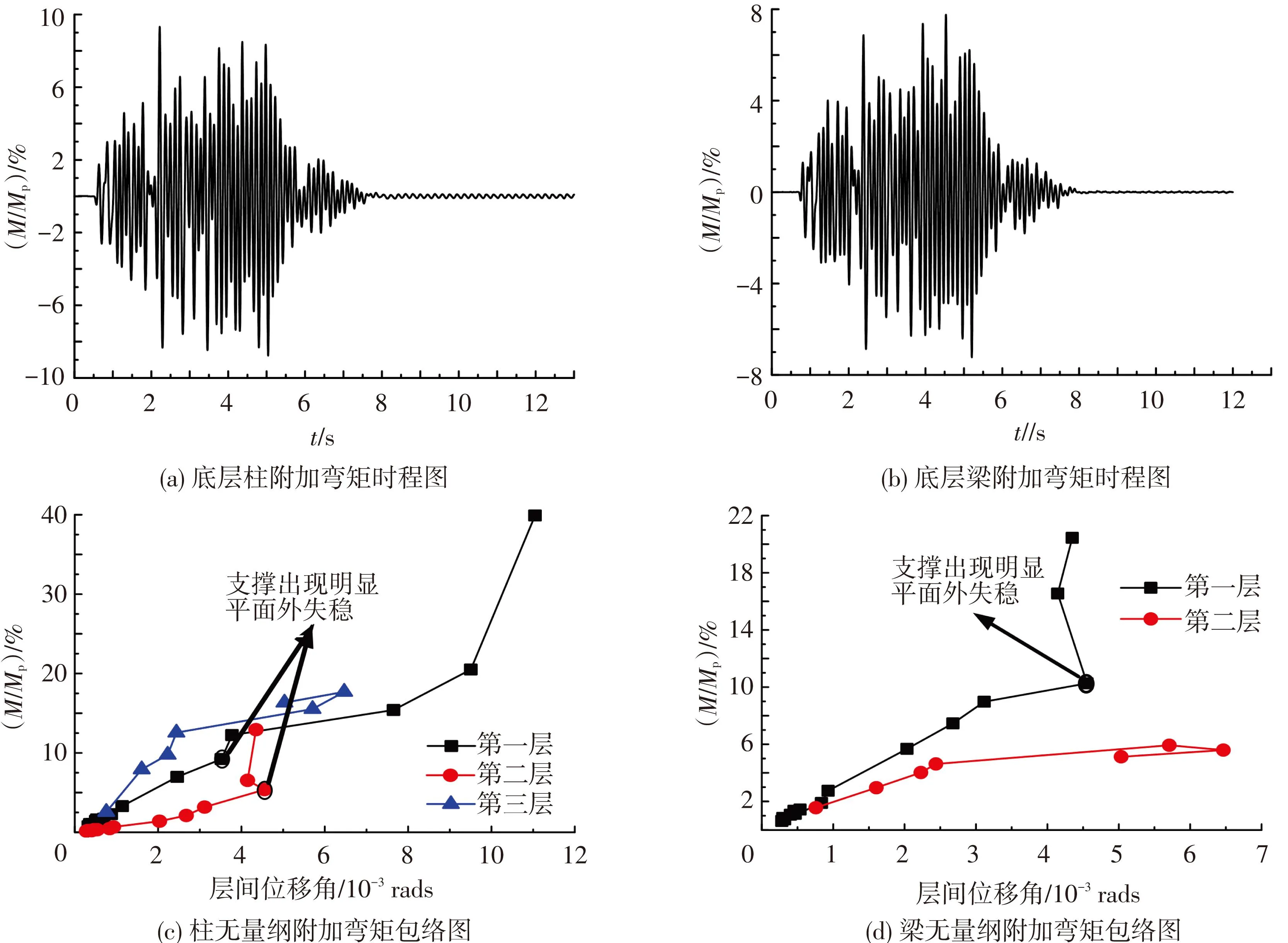
图10　梁柱附加弯矩

%

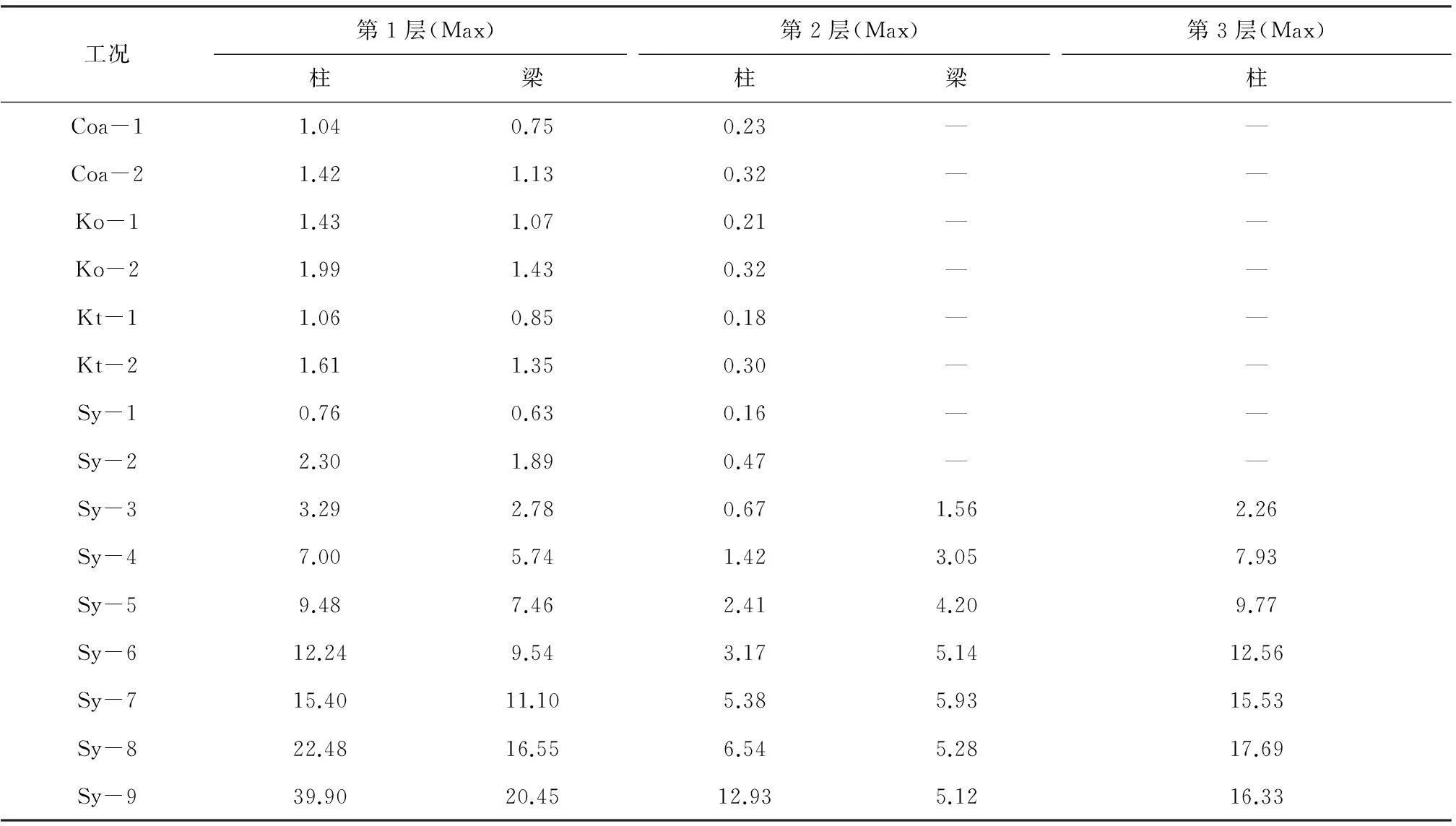
注：表中“—”表示由于采集设备的原因，没有采集到数据.

从图10(c)、(d)可明显看出，在支撑没有发生明显的平面外失稳前，梁、柱上附加弯矩随着层间位移角的增大而增大，两者基本呈线性关系；但是当增大到一定程度后，附加弯矩不再增大，底层梁、柱上附加弯矩都维持在10%左右；而当支撑发生平面外失稳以后，梁、柱上的附加弯矩急剧增大，不再是线性关系.当底层的层间位移角达到1/90.5时，底层柱上附加弯矩已经达到了39.9%，底层梁的附加弯矩达到20.5%.第3层作为拉链柱的传力桁架，设计时对支撑截面进行了加强，不允许其发生失稳，因此第2层梁、第3层柱上的附加弯矩没有发生急剧增加现象，最后柱上附加弯矩维持在15%，梁上附加弯矩维持在5%左右.

4.4节点板应力和梁柱在节点板处的局部应力

保证节点板不先于支撑发生破坏，满足强节点、弱构件的抗震设防要求是本试验研究的目的之一.判断这一目的是否实现，除了节点板及连接不先于支撑发生破坏，还需要保证在支撑发生平面外失稳之前，节点板依然处于弹性状态.将图3所示的节点板上每一组应变花的三向应变通过第四强度理论换算成等效主应变，给出其包络值与输入加速度的关系，见图11、12.提取节点区附近梁柱翼缘和腹板上采集到的应变值，分析该区域梁柱上局部应力的分布情况，见图13，其中梁、柱翼缘和腹板的应力结果为图3所示受力较大处应变片测量结果的包络值.

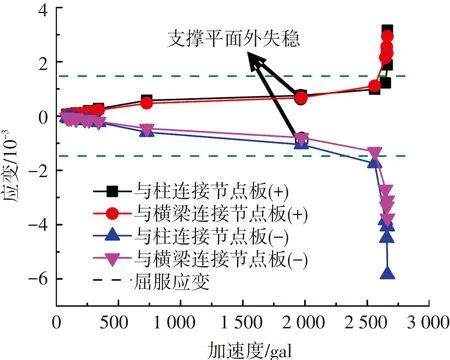
图11　底层节点板应变包络值-加速度曲线

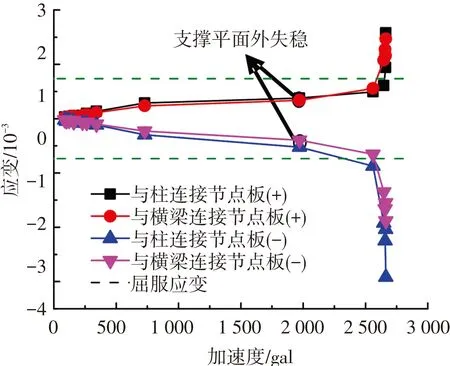
图12　第2层节点板应变包络值-加速度曲线

可以看出，节点板上的应变在支撑发生平面外失稳之前基本呈平缓的线性增长，并没有达到钢材的屈服应变.当支撑达到平面外失稳点后，曲线变陡，应变值增大，特别是随着支撑失稳变形越严重，节点板上应变增长越快，很快就超过了钢材的屈服应变.比较节点板正、负向应变值发现，支撑失稳后负应变数值的增长量明显大于正应变，原因是节点板面外弯曲后凹面处的弯曲应变与轴压应变叠加，而凸面处则处于相抵消的状态，见图7(b)、(c).梁柱上局部应力与节点板上应变的变化规律相似，在支撑失稳之前基本呈线性、且增长缓慢，支撑失稳后变化加剧.翼缘和腹板上的应力值相差不大，多次罕遇地震动作用下都没有达到钢材的屈服强度.

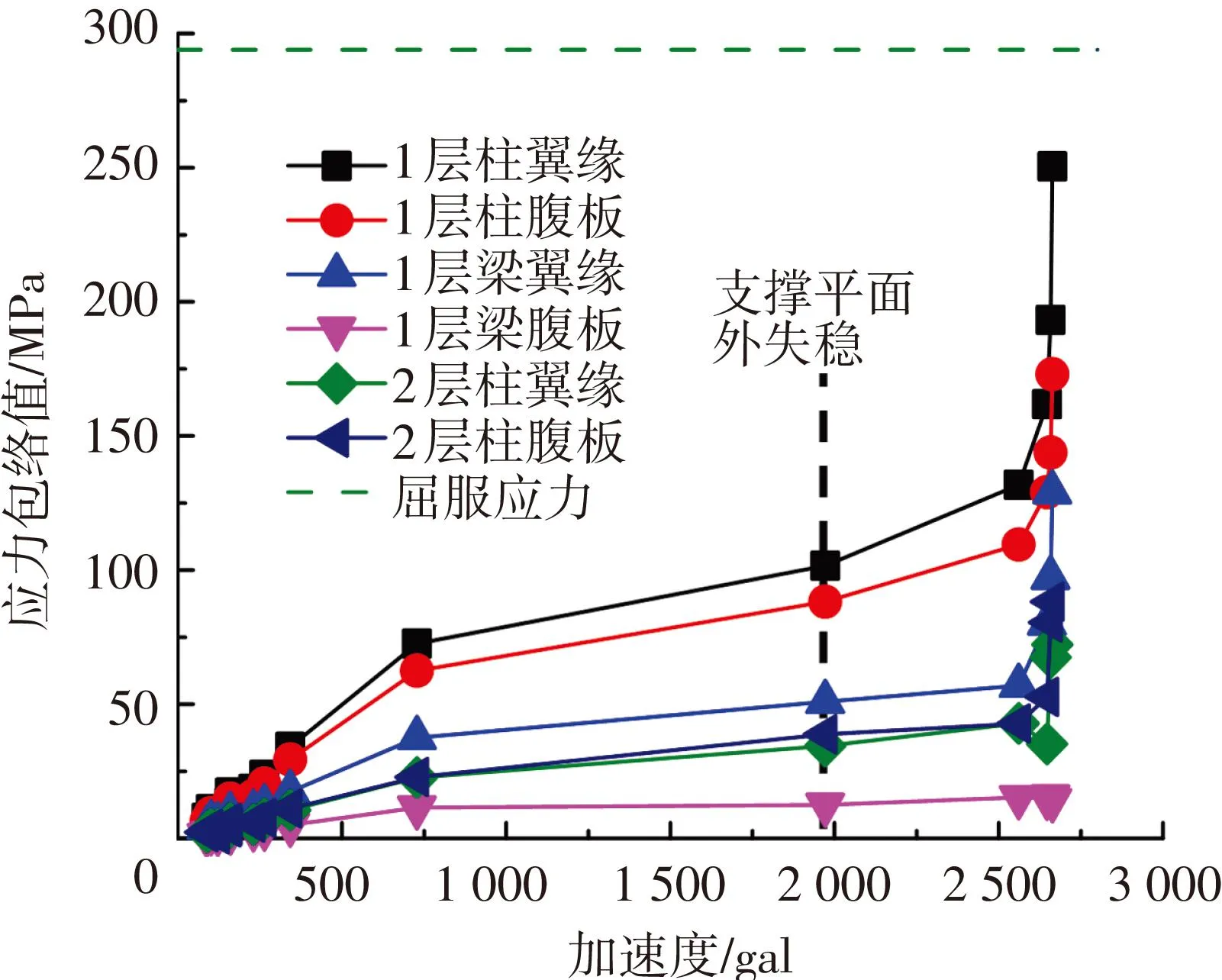
图13　梁柱局部应力包络值-加速度曲线

5结论

1)中心支撑及其节点，在试验中表现出较好的承载力、延性和耗能能力，板式连接节点发挥了预想的屈服和变形机制，不但9度罕遇地震中未发生倒塌，甚至在多波连续强震作用时仍然具有一定的安全储备.

2)各层相对位移在多遇地震作用时基本呈线性关系，结构弹性地震响应基本以一阶振型为主，但强震下底层层间位移角明显比2、3层有较大幅度的增加，表明底层为最不利位置.

3)在多遇地震动作用时，附加弯矩普遍不大，一般不超过3%；在支撑没有明显失稳前，随着层间位移角的增大而增大，并趋于某一固定值(底层梁、柱10%，2层梁5%、3层柱15%)；当支撑发生失稳以后，附加弯矩急剧增大，底层柱上附加弯矩可达40%，梁上可达20.5%.

4)在支撑发生面外失稳之前，节点板上应变及梁柱局部应力在弹性范围内呈缓慢的线性增加；支撑失稳后，节点板上的应变加剧并很快就超过了屈服应变；而节点区域梁柱基本没有进入塑性.

5)在多次强震作用下，虽然支撑反复多次失稳并进入塑性，但节点板仅沿着净距上的塑性铰线发生了平面外转动，节点处并未发生任何开裂，证明了节点连接抗震设计方法是可行性.

参考文献

[1] 张文元, 陈世玺, 张耀春. 支撑与梁柱板式连接节点低周疲劳分析及设计方法研究[J]. 工程力学, 2011，28(1):96-104.

[2] YU Haifeng, ZHANG Wenyuan, ZHANG Yaochun,et al. Shaking table test and numerical analysis for a 1∶12 scale model of special concentrically braced steel frame with pinned connections[J]. Earthquake Engineering and Engineering Vibration, 2010,9(1):51-63.

[3] 钢结构设计规范：GB 50017—2003[S]. 北京:中国计划出版社, 2003.

[4] 建筑抗震设计规范：GB 5011—2010[S]. 北京:中国建筑工业出版社, 2010.

[5] 建筑工程抗震性态设计通则(试用)：CECS160:2004[S]. 北京:中国计划出版社, 2004.

[6] WHITMORE R E. Experimental investigation of stresses in gusset plates[R]. Bulletin No. 16. Knoxville: Engineering Experiment Station, University of Tennessee, 1952.

[7] ASTANEH-ASL A, GOEL S C. Cyclic in-of-plane buckling of double angle bracing[J]. Journal of Structural Engineering, 1984, 110(9): 2036-2055.

[8] THORNTON W A. Bracing connections for heavy construction[J]. Engineering Journal, AISC, 1984, 21(3):139-148.

[9] 张文元, 周宇, 张耀春. 支撑节点板对铰接框架梁柱附加弯矩的影响[J]. 哈尔滨工业大学学报, 2013,45(6): 1-7.

[10]Specification for structural steel buildings：ANSI/AISC 341-10[S]. Chicago (IL): American Institute of Steel Construction, 2010.

(编辑赵丽莹)

Shaking table test of special concentrically braced steel frame with pinned connections

ZHANG Wenyuan1,2, MAI Hao1,2,YU Haifeng3

(1.Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education,150090 Harbin, China; 2. School of Civil Engineering, Harbin Institute of Technology, 150090 Harbin,China;3.School of Civil Engineering, Hebei University of Science and Technology, 050018 Shijiazhuang, China)

Abstract:The one-bay and three-story concentrically braced frame built in the zone with a seismic design intensity of 8 degree was constructed with 1∶4 scale, and tested using shaking table under 24 different earthquake ground motions to explore the seismic performance of special concentrically braced frame with pinned connections and the failure mode of braced system. The influence of the secondary moments on the columns and the beams was obtained. The results show that, the test model under intensity 8 frequent and rare earthquakes are all less than their limit values pursuant to the GB 50011—2010 code. The structure not only survived after the rare earthquake, even owned a certain security reserve after a series of strong earthquakes. It indicates that the structure system owns good seismic performance in the high seismic region. The secondary moments on the columns and the beams induced by the gusset plate connections become significant especially after the out-of-plane buckling of the braces. Based on the test results under a series of strong earthquakes, the seismic design principle, e.g. strong-connection-weak-member in the braces, is perfectly achieved.

Keywords:special concentrically braced frame; shaking table test; failure mode; secondary moment; seismic performance

中图分类号:TU398

文献标志码:A

文章编号:0367-6234(2016)06-0017-08

通信作者:张文元，hitwy@163.com.

作者简介:张文元(1972—)，男，教授，博士生导师.

基金项目:国家自然科学基金面上项目(51178145，51208169)；

收稿日期:2015-03-10.

doi：10.11918/j.issn.0367-6234.2016.06.003

河北省自然科学基金(E2014208115).