一种鲁棒的散焦模糊图像点扩散函数参数估计方法

梁　敏,徐彤阳,张人上

(山西财经大学信息管理学院, 太原 030031)



一种鲁棒的散焦模糊图像点扩散函数参数估计方法

梁敏,徐彤阳,张人上

(山西财经大学信息管理学院, 太原 030031)

摘要：提出了一种具有较强抗噪能力的频率域鉴别散焦模糊参数的方法。该方法对模糊图像对数频谱图实施极坐标变换，然后计算距频谱中心不同半径下的多方向幅值累加和函数，进而提取第一过零圆环的半径，完成散焦模糊参数的估计。实验结果表明，该方法能够适应带噪散焦模糊图像退化模型的参数估计问题，且具有较高的鉴别精度。

关键词：散焦模糊；图像复原；点扩散函数；参数估计

0引言

图像盲复原的质量在很大程度上取决于对退化过程先验知识(如点扩散函数)的了解程度。然而，实际应用中对图像退化点扩散函数的了解十分有限，需要由待测模糊图像进行估计。针对散焦模糊图像复原点扩散函数参数未知的情况，有学者在空域借助于边缘扩散信息进行估计，这类方法的前提是图像中存在强边缘[1-2]。考虑到散焦模糊图像在频域显著的频谱特征，频域估计参数的方法受到了广泛的关注。较为典型的方法有：散焦模糊频谱图的对角线方向检测频域零点估计模糊半径[3]，利用二次模糊进行频谱相关系数分析估计参数，可以实现自动识别[4],采用Hough变换检测相邻极小值点的比值来估计散焦参数[5-6]；以及在倒谱域[7]中鉴别极小值点实现参数的估计方法。上述方法在模糊尺度较小、图像信噪比较高时具有良好的鉴别精度，一旦模糊尺度加大或者噪声干扰加重时，无法提供可靠的参数估计。

本文提出一种鲁棒的散焦模糊参数估计方法。通过考察散焦模糊图像频谱图的多方向幅值累加和提取第一过零圆环的半径，进而计算得到散焦模糊参数的估计，能够为噪声环境下模糊图像点扩散函数提供精度较高的参数估计。

1退化模型的频域特征

一般空不变图像退化模型可以表示为：

g(x,y)=h(x,y)*f(x,y)+n(x,y)，

(1)

式中：g(x,y)为退化图像；f(x,y)为原始图像；h(x,y)是点扩散函数(PSF)；n(x,y)表示噪声项；符号“*”表示卷积运算。

散焦半径为R的PSF可以表示为[8]：

(2)

式(2)对应的傅里叶变换为:

(3)

式中J1(·)表示一阶第一类Bessel函数。

Bessel函数以接近π的间距存在无穷多单重零点。因此在散焦模糊图像图1(b)的频谱图(图1(c))中可以观察到类周期性的圆环。散焦半径R和第一圆环的半径dr满足以下关系[9]：

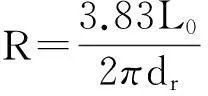
(4)

式中L0×L0为图像做傅里叶变换的尺寸。

图1显示了散焦模糊图像频谱图中出现的周期性暗色圆环，当模糊图像中存在噪声时，噪声破坏了对应频谱图中暗色圆环的周期性，当噪声强度进一步增大时，中心第一暗色圆环的边缘轮廓被弱化，增加了辨识的难度(图1(d)～图1(f))，从而导致散焦模糊参数的判别结果产生较大偏差，为此，针对带噪散焦模糊图像，提出一种基于频域极坐标变换的散焦参数估计方法。

(a)原始清晰图像(b)散焦图像(R=10)(c)图(b)频谱(d)方差0.01带噪频谱(e)方差0.05带噪频谱(f)方差0.1带噪频谱

图1 散焦模糊图像及其带噪频谱

2频谱判参法

考察散焦模糊图像的对数频谱图上多方向频谱幅值的特性。这里，假定(x0,y0)表示频谱图的中心，用极坐标表示频谱得到的函数，记为S(r,θ),其中S是散焦模糊图像的频谱函数，r、θ是极坐标系中的变量。对于每一个频率r，我们可以将Sr(θ)看成是一个一维函数，表示沿θ方向、距离中心半径为r的频谱表示。如果对θ变量在[0,φ]区间进行求和，可以得到S(r)：

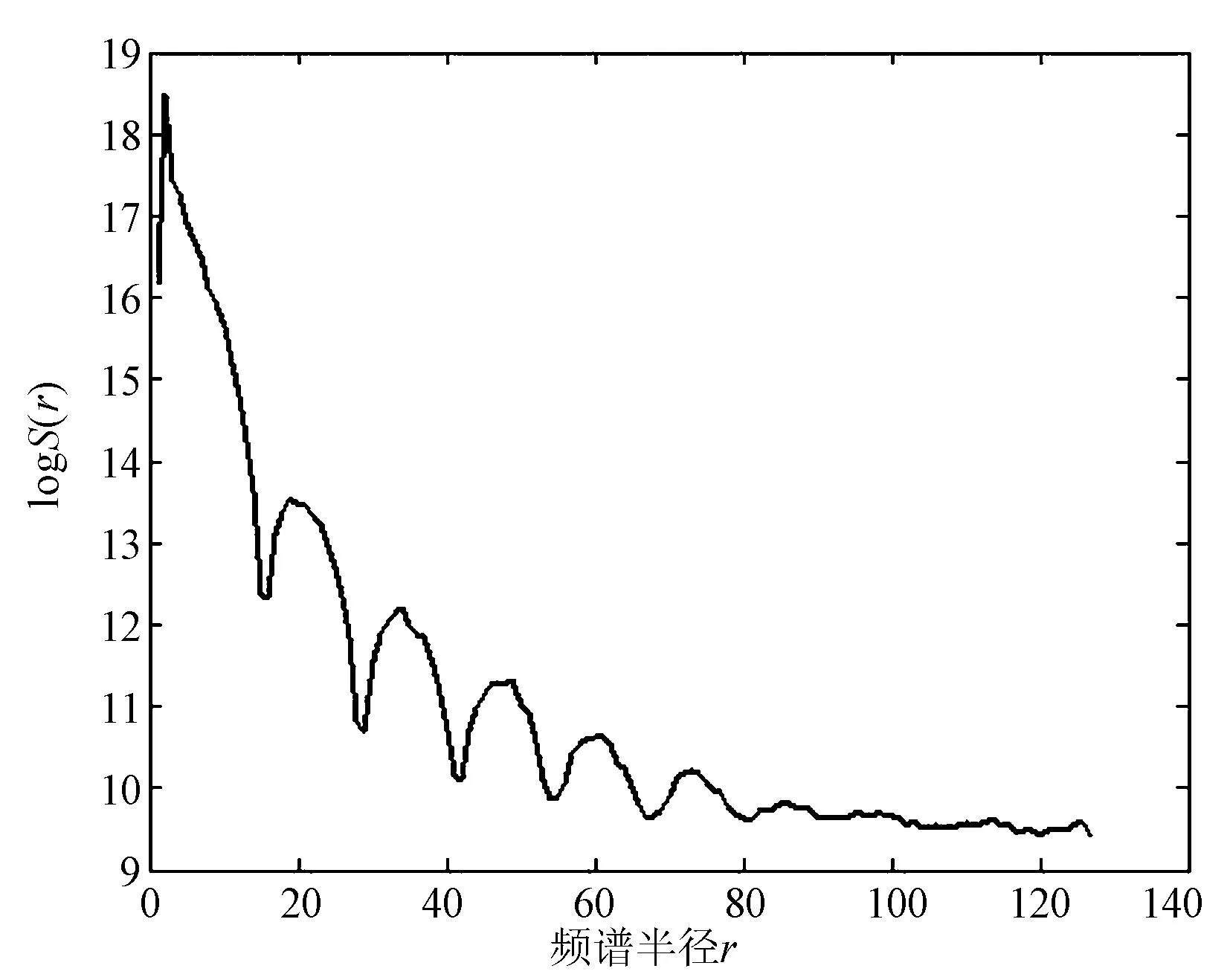
(a) 图1(c)logS曲线图

(b)图1(d)logS曲线图

(c)图1(e)logS曲线图

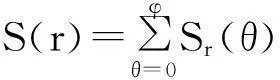
(5)

式中0<φ≤2π，那么S(r)可以得到以原点为中心的半径为r的多方向幅值累加的频谱特性。当r在一定范围内变化时，可以得到不同半径r下模糊图像的频谱幅值曲线S(r)。那么，频谱图中周期性的暗色圆环必然体现在S(r)的极小值位置，半径为dr的第一过零圆环则对应极小值中的最靠近原点的位置。

以图1(c)为例，计算S(r)函数，考虑到S(r)的取值范围很大，使用对数变换获得显著的曲线波动效果(图2(a))，从图中可以看到曲线呈现了显著的周期性起伏，波峰波谷的界线清晰，靠近原点的第一波谷位置明显。图2(b)～图2(c)给出了添加了噪声的图1(d)～图1(e)的logS(r)曲线效果图，可以看到，噪声破坏了远离原点的周期性起伏，外层的波峰波谷逐渐变得平坦甚至消失，而靠近原点的起伏受到噪声的影响较小，特别是靠近原点的第一波谷被保留了下来，该位置对应频谱图中的半径为dr第一过零圆环位置，散焦模糊参数R得以计算。

这是由于通过对多个方向幅值的求和计算，增强了到频谱中心的距离为r的频谱位置的特性。噪声对单一方向幅值的改变，可以通过多方向幅值的计算得到平均，因此，本文算法可以适用于带噪散焦

模糊参数的估计。

基于以上讨论，具体的算法步骤如下：1)首先对待测模糊图像进行傅里叶变换，并取对数，这样就可以得到模糊图像的对数频谱图像，其由一系列周期性的同心圆环组成。2)将对数频谱图的中心位置当作极坐标的原点，并由公式(5)计算S(r)函数，这里r的取值范围为[2，min(M/2,N/2)-1]。3)对S(r)求对数，靠近原点的r*=argminlog(S(r))，即为第一过零圆环的半径dr估计值。4)根据公式(4)计算散焦模糊参数R，即可得到散焦半径的估计值。

3实验结果

为了验证算法的有效性和鲁棒性，这里，重点考察带噪散焦模糊图像参数估计。下面，使用标准图像camera生成多幅仿真模糊带噪图像进行比较测试，获得参数估计值后采用维纳滤波进行复原。

3.1噪声情况下的判参实验

考察对噪声的适应性，对添加了不同程度(R=0～50)的散焦模糊以及方差在0.000 1～0.1变化的高斯噪声的camera图像估计了模糊半径，鉴别结果如图3所示，其中鉴别误差是绝对误差，计算公式为：误差=散焦半径估计值-真实半径，然后取其绝对值。

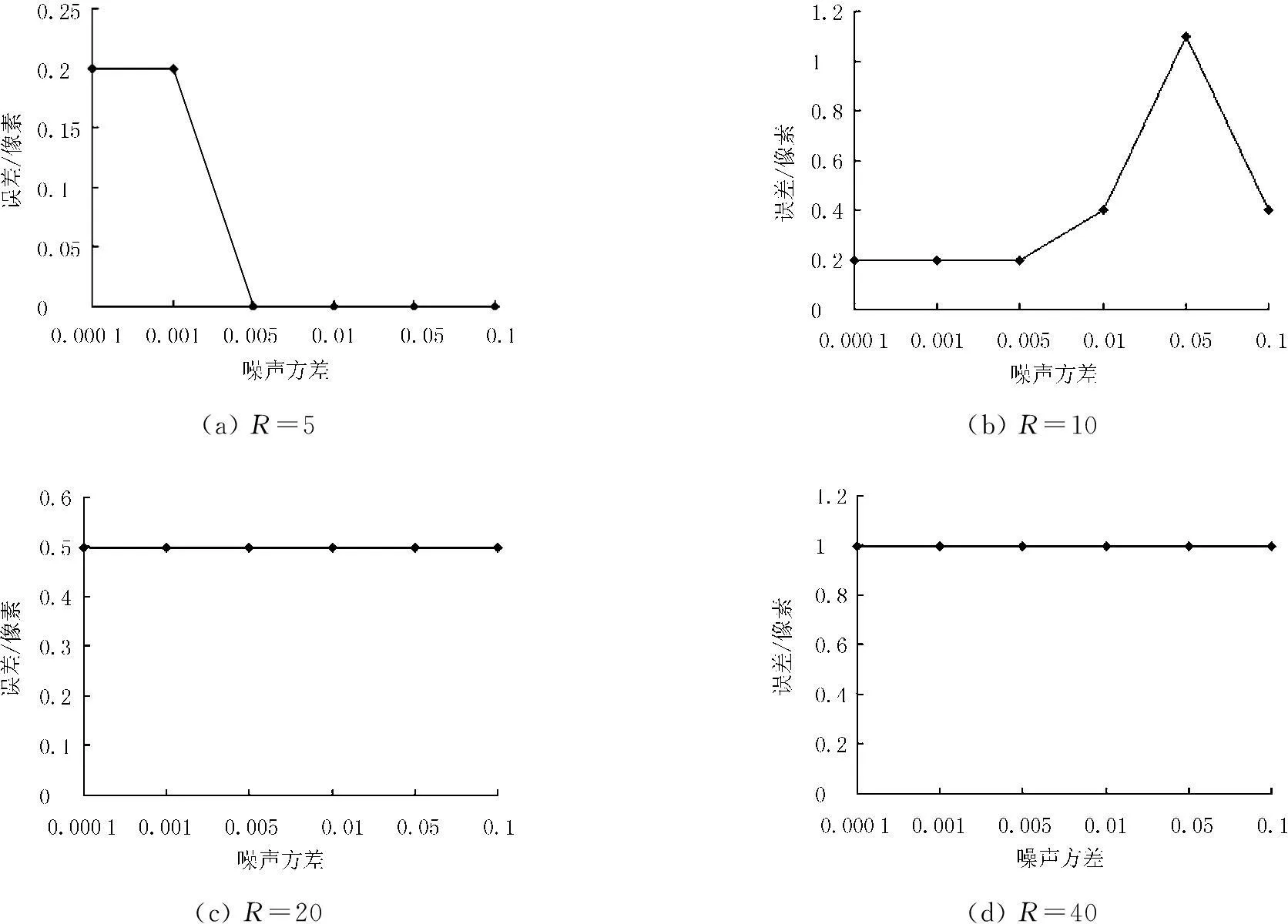
(a)R=5(b)R=10(c)R=20(d)R=40

图3鉴别出的散焦半径的绝对误差随噪声方差的变化曲线

综上所述可以得到结论：1)散焦模糊尺度的大小影响鉴别误差。随着散焦模糊程度的增大，鉴别误差呈现增大的趋势。2)噪声方差在0.000 1～0.1区间内，散焦模糊尺度在0～55之间，鉴别出的散焦半径的绝对误差在2个像素内，鉴别误差小，精度较高。3)噪声方差的大小对鉴别误差的影响可以忽略。如图3(c)～图3(d) ，随着噪声方差的增大，鉴别误差不变，说明本文算法对噪声有较强的鲁棒性。

3.2噪声情况下的对比实验

表1～2给出了采用典型算法和本文算法进行散焦参数估计的对比结果。表1为固定散焦模糊半径R=8，模糊图像加入均值为0，不同方差的高斯白噪声后，进行参数鉴别的测试实验。实验结果表明，倒谱[7]方法无法获取可靠的参数，其抗噪能力最低，文献[4]的方法在方差不大于0.04时，判参误差在一个像素以内，本文方法的误差在0.2个像素以内，但是当噪声强度进一步增大，文献[4]无法获取可靠参数，而本文方法的误差在1.2个像素以内。

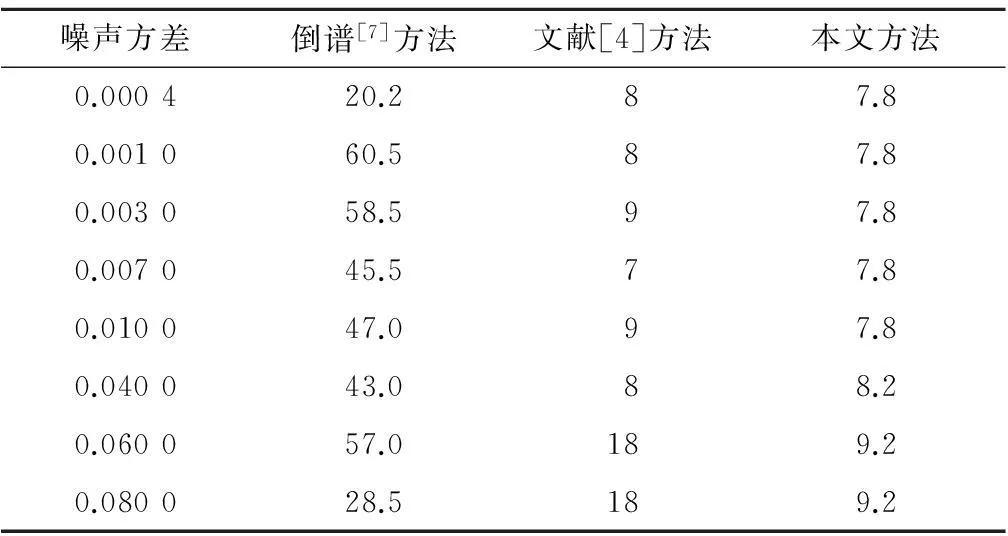
表1　R=8 camera散焦模糊图像加入均值为0，

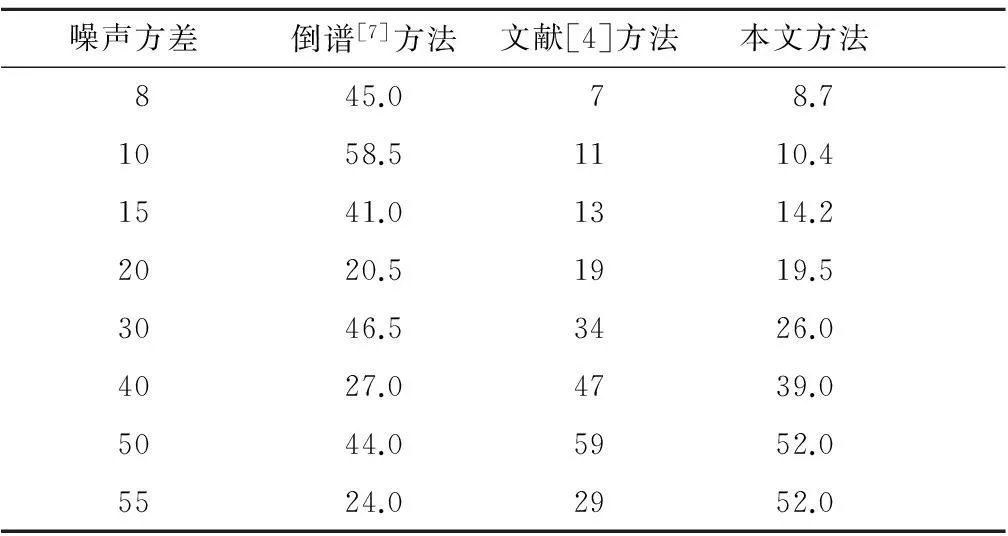
表2　0.05 噪声下不同尺度camera

表2为加入均值为0，方差为0.05的高斯白噪声，对不同散焦半径下的参数估计实验。实验结果表明，倒谱[7]方法无法适应这个强度的噪声。文献[4]对模糊半径在40以上时，无法获取可靠参数，而本文方法的鉴别精度和稳定性能是最优的。

3.3噪声情况下复原效果对比实验

为了更直观地对比实验结果，给出了使用倒谱[7]方法，文献[4]和本文方法分别鉴别出的PSF参数，运用经典维纳滤波复原方法的复原效果图。其中camera模糊图像的相关参数为：散焦模糊半径=8，噪声方差=0.003。图4(c)、图4(e)、图4(g)分别给出了倒谱方法[7]，文献[4]和本文方法的判参曲线，图4 (d)、图4(f)、图4(h)是响应的复原图像。对比3个算法的复原效果，可以看到图4(d)由于判参误差太大，复原图4(d)视觉效果最差，复原图4(f)有一定的复原效果，但由于参数不准引起的虚假轮廓较为明显，而本文的复原图像虚假轮廓被有效的减轻，复原质量得到了提高。

(a)原始图像

(b)散焦带噪图像

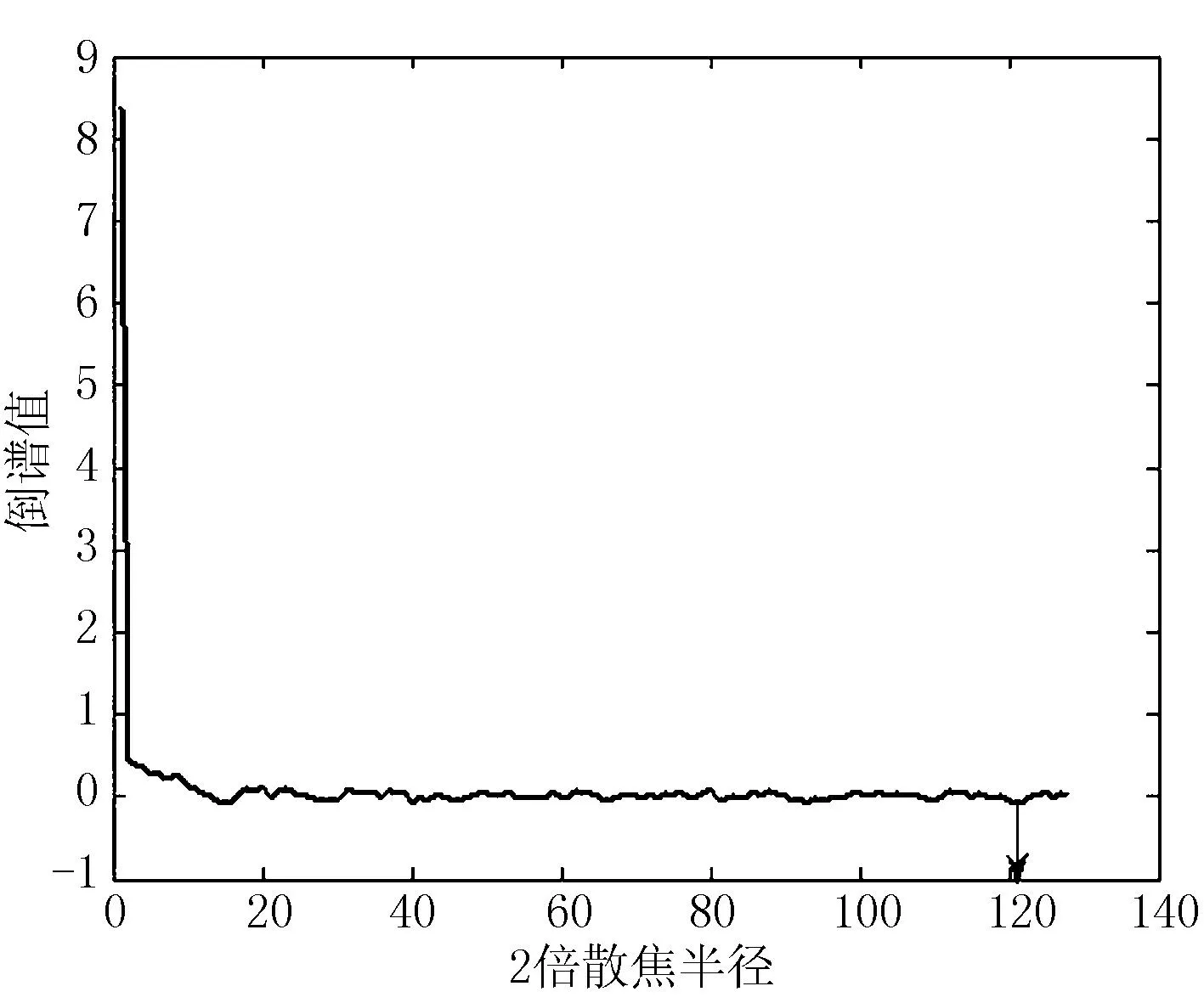
(c)倒谱[7]方法

(d)复原图像

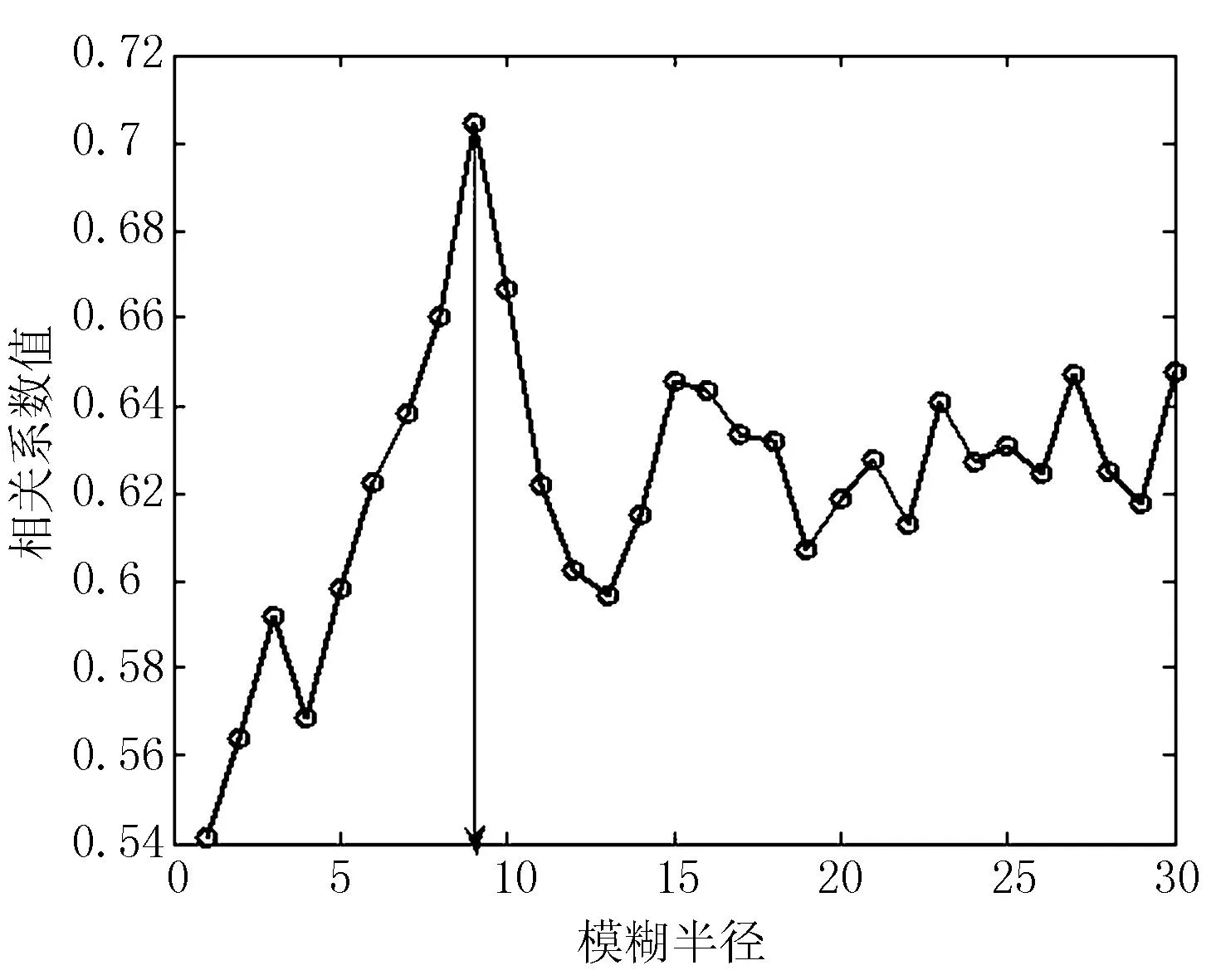
(e)文献[4]判参法

(f)R=9　nsr=0.01复原图像

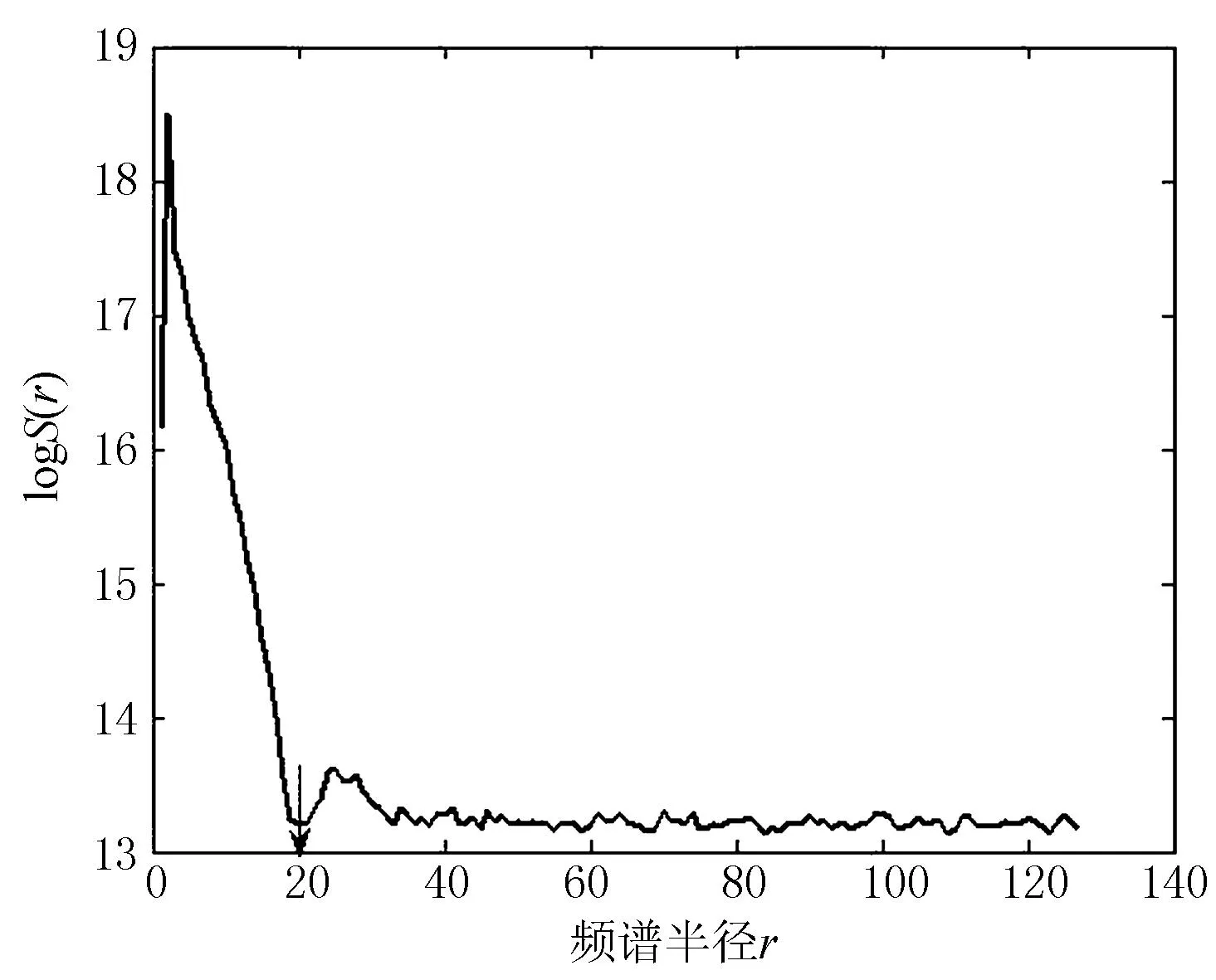
(g)本文方法

(h)R=7.8　nsr=0.01复原图像

4结语

本文提出了一种具有较强抗噪能力的频率域鉴别散焦模糊参数的方法。该方法对噪声方差在0.000 1～0.1区间内，散焦模糊尺度在0～55之间的多幅不同模糊图像进行参数鉴别，鉴别出的散焦半径的绝对误差在2个像素内，在强噪声环境下具有较高的判参精度，而且对较大尺度的模糊图像的参数鉴别精度的稳定性良好。通过大量的测试和比对实验，可以证实本文方法可以为散焦模糊图像复原提供更为精确的参数支持。

参考文献

[1] Wu Shiqian,Lin Weisi.Defocus estimation from a single image[C]//Proceedings intermational conference on computer communications and networks, ICCCN, St. Thomas, US Virgin Islands ：IEEE，2008:935-939.

[2] WuS,Chen L,Lin W,et al.An objective out-of-focus blur measurement[C]// Proceeding of the. fifth int. conf.information, communications and signal processing,bangkok：IEEE,2005:334-338.

[3] 王伟,方勇.单通道散焦模糊置换图像的盲分离[J]. 中国图象图形学报，2012,17(1):62-67.

[4] 周曲,颜国正,王文兴.相关系数分析在模糊图像参数识别中的应用[J].光学精密工程, 2007, 15(6):988-995.

[5] 周箩鱼,张葆,杨扬,等.采用Hough变换的离焦模糊参数的估计[J].红外与激光工程, 2012,41(10):2833-2837.

[6] 梁宛玉.多重模糊图像处理与恢复算法的研究[D].南京:南京理工大学,2011.

[7] 周曲,颜国正,王文兴.基于倒谱分析的散焦模糊图像参数识别[J].武汉大学学报:信息科学版,2008,33(3):318-321．

[8] 朱虹,欧阳光振,梁敏，等.一种基于参考图频谱相关的模糊参数判别方法[J].仪器仪表学报, 2012,33(8):1837-1843.

[9] 邹谋炎.反卷积和信号复原[M].北京：国防工业出版社,2001.

One Robust Parameter Estimation Method of Point Spread Function from Defocus Blurred Image

LIANG Min, etc.

(SchoolofInformationManagement,ShanxiUniversityofFinanceandEconomics,Taiyuan030031,China)

Abstract：A robust parameter estimation method from defocus blurred image in frequency domain is proposed in this article. First, polar transformation is applied to the logarithmic power spectrum of the defocus image in the frequency domain. Then the defocus blur radius can be obtained by calculating the sum of the logarithmic spectrum along concentric circles in the polar coordinate. The experiment results show that the proposed method can adapt to parameter estimation for deteriorate model with Gaussian noise blurred images and has high identifying accuracy.

Key words：defocus blur; image restoration; point spread function; parameter estimation

文献标志码：A

文章编号：1009-8984(2016)01-0109-05

中图分类号：TP391.41

作者简介：梁敏(1979-)，女(汉)，山西忻州，博士，副教授

基金项目：山西财经大学青年科研基金项目(QN-2014028)山西省哲学社会科学“十二五”规划2015年度课题(2015.10)

收稿日期：2016-03-03

doi:10.3969/j.issn.1009-8984.2016.01.025

主要研究图像处理。