定角圆锥扫描式机载激光测深系统定位模型与精度评价

李　凯，张永生，童晓冲，申二华

信息工程大学地理空间信息学院，河南 郑州 450001



定角圆锥扫描式机载激光测深系统定位模型与精度评价

李凯，张永生，童晓冲，申二华

信息工程大学地理空间信息学院，河南 郑州 450001

摘要：从定角圆锥扫描式机载激光测深系统激光测距仪内部结构出发，推导了棱镜、大气、海水中激光光线方向矢量方程，结合GPS/INS定位定姿系统，推导出激光脚点在成图坐标系中的定位模型。充分考虑对机载激光测深系统定位精度产生影响的各个因素，通过误差传播定律给出了圆锥扫描式机载激光测深系统的综合精度评价模型。参照国际上应用广泛的相关仪器系统参数、指标，对机载激光测深系统的定位精度进行实际计算，并对定位模型中涉及的主要误差源进行分析和讨论。

关键词：定角圆锥扫描；机载激光测深；定位模型；精度评价

机载激光扫描测距是一种直接对地定位的遥感技术。它将姿态测量装置、差分GPS、激光测距仪等技术产品集成一体，可以直接获取地面三维信息[1]。将地形扫描激光波长由红外波段(1064 nm)倍频至蓝绿波段(532 nm)，同时优化激光回波信号接收装置，可将机载激光扫描测距技术应用于浅水(0～50 m，水深与水质有关)测量[2]。

对激光测深技术而言，精确测量激光脚点在海底的三维坐标是其最基本，也是最主要的目的。然而由于GPS、INS、LiDAR的高度集成，系统必然受到距离、姿态、硬件磨损等各种系统误差和偶然误差的影响。文献[3]说明了利用GPS、IMU、扫描激光测距对地定位的基本原理、重点分析了各个误差项及其对定位结果的影响,并进行了误差传播和精度估计。文献[4]论述了机载激光测距的定位原理，并讨论了与机载激光测距的对地定位精度有关的传感器的误差对系统定位精度的影响。文献[5]分析了机载三维成像仪获取的数据结构，给出了计算激光测距点位置的具体步骤，最后通过算例说明了计算方法的正确性。文献[6]对影响机载激光测深精度的附属误差和海水深度的测量误差进行了分析。文献[7]推导了条带式深度测量测点位置归算的严密计算公式及其相应的精度估算公式，并对位置归算改正的量值大小进行了数值计算和精度评定。国外也有不少学者对影响机载激光扫描测距系统的定位模型进行了分析[8-11]。但是这些文献中所提到的圆锥扫描模式并非严格意义上的圆锥扫描，因为反射镜法线与转轴之间存在一定的夹角T,当反射镜在驱动电机的驱使下高速旋转时，反射镜法线在空间形成一个顶角为2T的圆锥体。而激光脚点在地面上的分布是呈一头略大、一头略小的“类椭圆扫描”[12]。同时，这些文献较少考虑激光、扫描仪、光学棱镜之间的安置误差。最后，考虑到机载激光测深与激光扫描测距的区别，还应考虑激光在水气界面传播时的折射以及测量误差随水深的变化情况。

激光测深系统的激光扫描装置通过扫描镜的局部运动，实现激光测深点的条带式测量。一般而言，激光测深扫描模式分为直线扫描、椭圆扫描和圆锥扫描，圆锥扫描相比直线扫描和椭圆扫描机械结构最为简单。为了提高测量效率,需要扫描装置高速运转,而机械结构越复杂,扫描运行就越不易平稳,但为确保测量点精确定位,必须保证扫描机构的平稳运行[12]。随着计算机技术的发展，数据处理的速度已经得到很大的提升，不需要再牺牲测量效率以换取更适于处理的数据。因此有必要采用机械结构简单的圆锥扫描模式以提高测量效率。本文以加拿大Optech公司研制的CZMIL(coast zone mapping and imaging LIDAR)[13]机载激光测深系统定角圆锥扫描结构为例，推导激光脉冲从发射器发射，经过棱镜出射，到达海面之后再由水面折射进入水体，最终在水底形成激光脚点的精确定位模型，同时推导出机载激光测深系统精度评价模型和数值模拟结果，并对定位模型中涉及的主要误差源进行分析和讨论。

1定角圆锥扫描式激光测深系统定位模型

CZMIL圆锥扫描式激光扫描仪的结构如图1所示[10]。在图1中所示的激光扫描坐标系中，原点位于具有一定倾角的棱镜上表面中心；Z轴垂直于棱镜下表面，向下为正；棱镜下为高速旋转的扫描仪，扫描仪与棱镜固连在一起。X轴指向飞机前进方向，Y轴指向飞机右翼。图1中所示位置为扫描初始位置，即扫描角为0°，激光发射器沿Z轴方向竖直向下发射激光脉冲，在棱镜表面被折射后进入棱镜，并从棱镜下表面出射，当棱镜随扫描仪高速旋转时，激光出射方向改变，而与Z轴夹角不变，形成一个圆锥。理想状态下，激光脚点在水平地面上的轨迹为圆形。

图1　激光发射器、棱镜、扫描仪安置示意图及其所在的激光扫描坐标系(原点O位于激光入射点)Fig.1　The schematic diagram of laser transmitter,prism,scanner assembly and scanner’s coordinate system(the point O represents Laser incident point)

1.1激光光线的向量表达

为方便分析，取图1的侧视图分析激光光线在棱镜中的传输，图2表示了激光光线在棱镜中的传输和通过平静海水面的折射效应。图2中各矢量和角度的关系如表1所示。

图2　激光光线在棱镜中的传输和在海平面的折射Fig.2　Transmission of a laser pulse in the prism and refraction of a laser pulse on the sea surface

1激光扫描仪中各部件之间安置角和激光光线矢量说明

Tab.1Explanation of placement angle and the laser light vector in the laser scanner

符号意 义θf棱镜上表面倾斜角l1、θ1、p1激光光线入射矢量、入射角和棱镜上表面法线矢量l2、θ2激光在棱镜内出射光线(也是棱镜下表面入射光线)矢量、出射角θ3、p2棱镜内激光光线入射角、棱镜下表面法线矢量l3、θ4激光在大气中的出射光线(也是海面入射光线)矢量、出射角nf、na、nw棱镜晶体折射率(1.461)、大气折射率(1.0003)、海水折射率(1.33)p3、l4、θ5静止海平面法线向量、激光通过海面后的光线出射矢量、出射角

由图2可知，θf=θ1。由文献[14]给出的折射定律的矢量表示形式，对于l2，有

cosθ1=-p1·l1

(1)

(2)

(3)

则

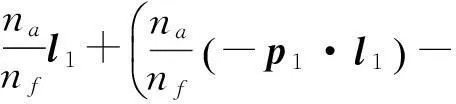
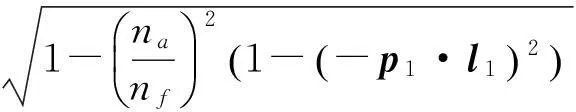
(4)

对于l3，有

cosθ3=-p2·l2

(5)

(6)

(7)

则

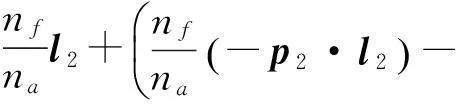
(8)

最后可得到进入海水(静止海面)后激光光线的传播方向为

(9)

又由于θ1=θ2+θ3，由折射定律及式(2)、式(6)可得到θ4和θ1的关系

(10)

根据预先设定的激光入射角θ4，由式(10)计算出棱镜上表面的斜坡坡度θf(θf=θ1)。如当激光入射角为20°时，棱镜上表面斜坡坡度为39.16°。

1.2激光扫描仪各部件之间的安置误差

当激光扫描仪中各部件(激光发射器、扫描仪、光学棱镜)严格对准时，根据图2，有

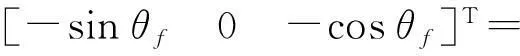
(11)

(12)

(13)

(14)

然而实际上，光学棱镜和扫描仪之间，激光发射器和扫描仪之间都存在安置角误差，另外式(11)—式(14)均为扫描方位角为0°时的表达式，这都使得式(11)—式(14)需要进一步修正。当光学棱镜和扫描仪坐标轴不能完全重合时，设由棱镜至扫描仪的x、y、z轴的旋转角分别为θfsx、θfsy、θfsz，对应的旋转矩阵为

(15)

(16)

(17)

当扫描方位角为θaz时

(18)

(19)

(20)

(21)

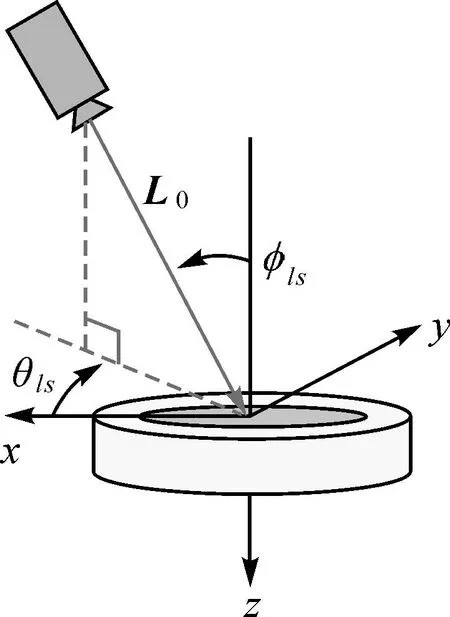
图3　激光发射器和扫描仪之间的安置误差Fig.3　Placement error between the laser transmitter and scanner

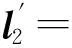
(22)

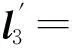
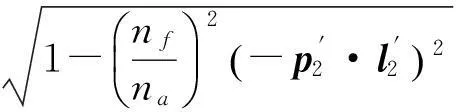
(23)

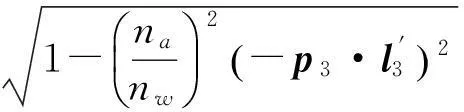
(24)

1.3激光脚点定位模型

设激光测深系统测得的激光在大气中传播的时间为Δt1，在海水中传播的时间为Δt2，由于棱镜厚度可忽略不计，不考虑激光在棱镜中的传输，可以得到在激光扫描坐标系中激光脚点在海底的位置为

(25)

式中，c=299 552 816 m/s为光在空气中传播的速度。

Xil=Ri·Xl+ΔXil=Riz·Riy·Rix·Xl+ΔXil

(26)

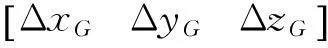
XG=Rv·Xil+ΔXG=Rvz·Rvy·Rvx·Xil+ΔXG

(27)

利用式(25)、式(26)中的参数替代式(27)，得到

(28)

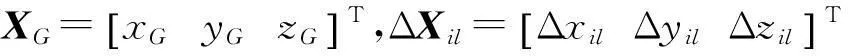
2影响激光点云的定位精度的各个误差源及标准差符号

Tab.2Error sources that affect the positioning accuracy of the laser point cloud and corresponding standard deviation symbols

参数误差源标准差符号激光发射器、扫描仪、棱镜间安置误差棱镜上表面坡度θf误差σθf棱镜、扫描仪安置角θfsx、θfsy、θfsz误差σθfsx、σθfsy、σθfsz 扫描角方位θaz误差σθaz激光发射器、扫描仪安置角ϕls、θls误差σϕls、σθls激光扫描仪外部的测时、测角、测距误差激光在空气和海水中传播时间Δt1、Δt2误差σΔt1、σΔt2视准轴偏角θrol、θpit、θhea误差σθrol、σθpit、σθhea 激光扫描中心至INS中心坐标Δxil、Δyil、Δzil误差σΔxil、σΔyil、σΔzil 飞机姿态角ω、ψ、κ误差σω、σψ、σκGPS/INS中心在成图坐标系坐标ΔxG、ΔyG、ΔzG误差σΔxG、σΔyG、σΔzG

2误差对定位结果的影响评价

2.1机载激光测深系统综合精度评价模型

表2中列出的各误差源共同影响激光测深系统最终的定位结果，这些误差既包括系统误差，也包括偶然误差。如棱镜和扫描仪之间的安置角误差既包括系统组装时棱镜安装错位导致的系统误差，也包含扫描仪中滚珠轴承的细微差异导致旋转时产生的随机误差。对于系统误差，可以通过严格的检校手段予以消除[15-16]。对于偶然误差可以利用测量平差的手段予以处理，进而得到激光脚点的最佳估计值[17]。由于偶然误差是难以完全消除的，而且这些误差综合在一起影响最终的定位精度，为了全面地评价姿态测量装置、差分GPS、激光测距仪系统的最终定位误差，可以通过误差传播定律推导激光脚点三维位置的综合误差

(29)

在以上与最终定位精度有关的21个参数中，激光扫描中心至INS中心坐标Δxil、Δyil、Δzil由全站仪多次观测平均获得，可以视为精确值，因此σΔxil=σΔyil=σΔzil=0。剩余的18个参数对于最终定位结果XG的偏导仍可分激光测距仪内部参数(θf，θfsx，θfsy，θfsz，θaz，φls，θls)和外部参数(Δt1，Δt2，θrol，θpit，θhea，ω，ψ，κ，ΔxG，ΔyG，ΔzG)两类求解。例如，对于θfsx，有

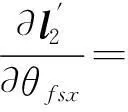
(30)

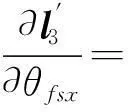
(31)

(32)

式中

(33)

(34)

由以上各式即可得到

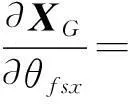
(35)

激光测距仪外部参数对于XG的偏导的推导与θfsx类似。例如对于ω，有

(36)

需要说明的是，在推导激光脚点三维位置的综合误差时，认为各参数之间相互独立，忽略了其相关性。实际上，有些参数之间是相互独立的，有些则不然。例如，激光测距时间Δt1、Δt2与扫描仪扫描方位角θaz之间是相互独立的，这是因为激光和扫描仪由不同厂家生产，其设备精度自然也互不相关；另一方面，姿态测量单元IMU获取的滚动偏角θrol和俯仰偏角θpit之间则一般具有相关性。然而，具有相关性的两个参数之间的协方差确定较为困难，当前国际上IMU生产厂家一般会提供滚动偏角、俯仰偏角、航向偏角的标准差或者方差，却很少提供不同角度之间的协方差数据。这也很有可能是早前对船载多波束和机载激光测深系统[7]以及机载遥感直接对地定位[3-4]精度评价时未考虑单个参数之间相关性的原因。如果利用最小二乘等方法对各项参数导致的误差进行系统性的检校，则可以获得不同参数之间的协方差矩阵，从而能够更加准确地对激光脚点三维位置综合误差进行评价。

2.2机载激光测深系统综合精度数值计算

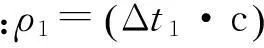
表3　部分参数的标准差数值

表4　各个参量对测点精度的影响

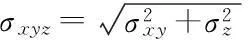
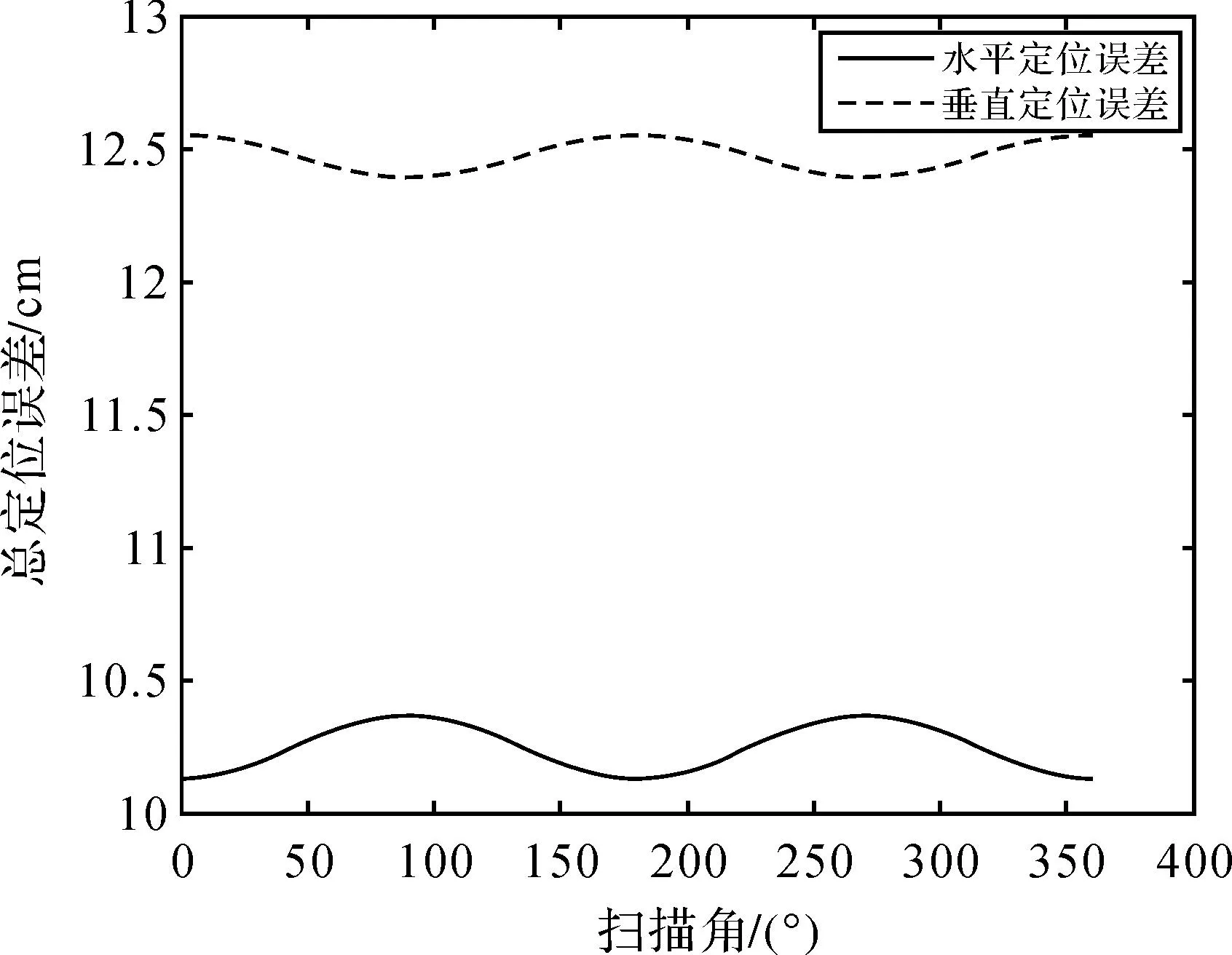
图4　不同扫描角θaz对定位结果的影响Fig.4　Effects of different scan angles to positioning results

3分析与讨论

(1) 由图4可以看出，随着扫描角的变化，水平定位误差和垂直定位误差呈现周期性的变化，这其实是由于影响激光脚点位置的各参数变化使激光脚点圆形扫描轨迹变化造成的。图5和图6分别表示激光扫描仪内部棱镜-扫描仪绕Y轴安置角为θfsy、激光与棱镜之间天顶角为φls时对定位结果的影响。图5中由于安置误差，当棱镜绕激光扫描仪坐标系的Y轴旋转θfsy角度时，激光扫描角度增大，扫描半径相应增大，但是随着扫描角度变化，棱镜也在旋转，因此扫描轨迹仍为圆形，各个脚点的平面位置和高程位置误差相同，不随扫描角度的变化而变化。图6中激光偏离Z轴φls角度射入棱镜，当扫描角度为0°时(图6(a))，激光出射光线(实线)较没有偏差(虚线)时更加靠近圆形扫描轨迹的圆心，而当扫描角为180°时(图6(b))，激光出射光线(实线)较没有偏差(虚线)时远离圆形扫描轨迹的圆心，此时激光脚点在地面上的轨迹变成类椭圆的卵形。因此随着扫描角度的变化，激光脚点的水平误差和垂直误差都不相同。同样，不难想象，当飞机以一定的滚动角ω或俯仰角ψ飞行时，激光脚点在水平地面(海面)上的落点将呈椭圆形，激光脚点的水平误差和垂直误差也随扫描角度的变化而变化。与之产生类似效果的还有视准轴偏角θrol、θpit。因此φls、ω、ψ、θrol、θpit这5个角度偏差共同决定了激光脚点平面、垂直位置误差随扫描角而产生的变化。

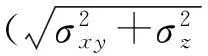
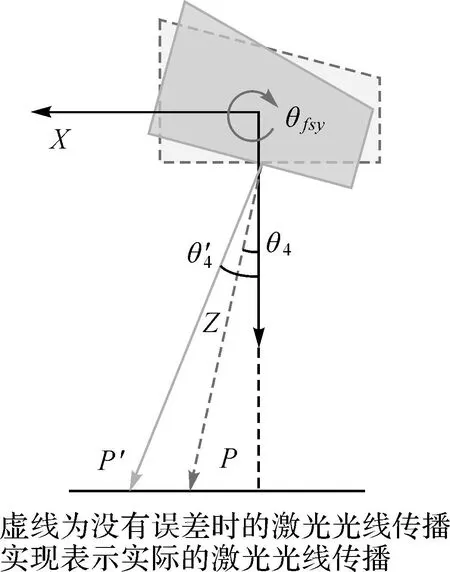
图5　棱镜-扫描仪绕Y轴安置角对激光脚点位置的影响Fig.5　Laser foot position error caused by Prism-Scanner placement angle around the Y axis

图6　激光与棱镜之间天顶角对定位结果的影响Fig.6　Laser foot position error caused by zenith angle between the laser and prism

(3) 本文是在固定的航高(400 m)和水深(50 m)情况下对激光脚点定位精度进行分析，实际上航高和水深变化时，激光脚点的定位精度也会发生变化，一般而言，正常飞行情况下飞机航高保持不变，这时定位精度是水深的函数，水深值越大，定位误差也越大(假设激光在海水传播的计时误差不随水深改变)。

4结束语

本文以加拿大Optech公司CZMIL定角圆锥扫描式机载激光测深系统为例，从激光测距仪内部结构出发，推导了激光传播方向矢量在棱镜、大气、海水中的变化，继而结合GPS/INS定位定姿系统，进一步推导了激光脚点在成图坐标系中的定位模型，通过误差传播定律对圆锥扫描式机载激光测深系统进行了综合精度评价。机载激光测深技术在国内的研究还比较滞后，本工作对此类技术设备在国内开展相关应用具有非常实际的意义。

要提高机载激光测深系统的定位精度，首先要解决的问题是激光在海水中传播时间的确定[21-23]，激光信号经由大气、海水、海底往返，尤其在海水中传播时与海水中各种成分作用复杂，光信号衰减迅速，从而导致海底回波信号中引入大量噪声，难以识别和提取，这也是需要进一步研究的难点问题。此外，要提高圆锥扫描式机载激光测深系统定位精度，还必须提高GPS定位精度，还应尽可能减小激光测距仪内部的安置误差。

参考文献：

[1]江月松.机载GPS、姿态和激光扫描测距集成定位系统的精确定位方程、误差分析与精度评估[J]. 遥感学报, 2001, 5(4): 241-247.

JIANG Yuesong. A Rigorous Positioning Equation and It’s Error Analysis and Precision Evaluation for Integrated Positioning System of Airborne GPS, INS and Laser Scanning Ranging[J]. Journal of Remote Sensing, 2001, 5(4): 241-247.

[2]翟国君, 王克平, 刘玉红. 机载激光测深技术[J]. 海洋测绘, 2014, 34(2): 72-75.

ZHAI Guojun, WANG Keping, LIU Yuhong. Technology of Airborne Laser Bathymetry[J]. Hydrographic Surveying and Charting, 2014, 34(2): 72- 75.

[3]尤红建, 江月松, 李树楷. 机载遥感直接对地定位的误差分析和精度估计[J]. 测绘学报, 1998, 27(1): 86-91.

YOU Hongjian, JIANG Yuesong, LI Shukai. Error Analysis and Accuracy Estimation of Airborne Remote Sensing with Air-to-ground Positioning System[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(1): 86-91.

[4]刘少创, 邵晖, 向茂生, 等. 机载三维成像仪的定位原理与误差分析[J]. 测绘学报, 1999, 28(2): 121-127.

LIU Shaochuang, SHAO Hui, XIANG Maosheng, et al. Positioning Principles and Accuracy of Airborne Laser-ranging and Multispectral-imaging Mapping System[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2): 121-127.

[5]尤红建, 刘少创, 刘彤, 等. 机载三维成像仪系统中激光点位置的解算及应用[J]. 遥感技术与应用, 2000, 15(3): 141-145.

YOU Hongjian, LIU Shaochuang, LIU Tong, et al. Calculating the Position of Laser Points of Airborne 3D Image and It’s Application[J]. Remote Sensing Technology and Application, 2000, 15(3): 141- 145.

[6]刘基余, 李松. 机载激光测深系统测深误差源的研究[J]. 武汉测绘科技大学学报, 2000, 25(6): 491- 495.

LIU Jiyu, LI Song. Application on Error Sources Surveying Sea-water Depths with an Airborne Laser Sounding System[J]. Journal of Wuhan Technical University of Surveying and Mapping, 2000, 25(6): 491- 495.

[7]黄谟涛, 翟国君, 谢锡君, 等. 多波束和机载激光测深位置归算及载体姿态影响研究[J]. 测绘学报, 2000, 29(1): 82-88.

HUANG Motao,ZHAI Guojun,XIE Xijun. The Influence of Carrier’s Attitude and the Position Reduction in Multibeam Echosounding and Airborne Laser Depth Sounding. Acta Geodaetica et Cartographica Sinica, 2000, 29(1): 82-88.

[8]FRIESS P. Toward a Rigorous Methodology for Airborne Laser Mapping[C]∥Proceedings of EuroCOW. Castelldefels: [s.n.], 2006: 25-27.

[9]SKALOUD J, SCHAER P. Towards Automated LiDAR Boresight Self-calibration[C]∥Proceedings of the 5th International Symposium on Mobile Mapping Technology. Padova: MMS, 2007.

[10]GONSALVES M O. A Comprehensive Uncertainty Analysis and Method of Geometric Calibration for a Circular Scanning Airborne Lidar[D]. Hattiesburg: The University of Southern Mississippi, 2010.

[11]MAY N C. A Rigorous Approach to Comprehesive Performance Analysis of State-of-the-art Airborne Mobile Mapping Systems[D]. Columbo: The Ohio State University,2008.

[12]任来平, 赵俊生, 翟国君, 等. 机载激光测深海面扫描轨迹计算与分析[J]. 武汉大学学报(信息科学版), 2002, 27(2): 138-142.

REN Laiping, ZHAO Junsheng, ZHAI Guojun, et al. Scanning-track Computation and Analysis for Airborne Laser Depth Sounding[J]. Geomatics and Information Science of Wuhan University, 2002, 27(2): 138-142.

[13]FUCHS E, MATHUR A. Utilizing Circular Scanning in the CZMIL System[C]∥Proceedings of the SPIE 7695, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVI. Orlando, Florida: SPIE, 2010.

[14]GLASSNER A S. An Introduction to Ray Tracing[M]. London: Academic Press, 1989.

[15]张靖, 江万寿, 姜三. 基于虚拟点模型的机载LiDAR系统自动检校方法[J]. 测绘学报, 2013, 42(3): 389-396.

ZHANG Jing, JIANG Wanshou, JIANG San. Automated Airborne LiDAR System Calibration Using Virtual Tie Point Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 389-396.

[16]HABIB A F, AL-DURGHAM M,KERSTING A P, et al. Error Budget of LiDAR Systems and Quality Control of the Derived Point Cloud[C]∥Proceedings of the 21st International Society for Photogrammetry and Remote Sensing Congress, Commission I. Beijing: [s.n.], 2008, 37(Part B).

[17]江延川.解析摄影测量学[Z]. 郑州: 解放军测绘学院, 1991.

JIANG Yanchuan. Analytical Photogrammetry[Z]. Zhengzhou: Zhengzhou Institute of Surveying and Mapping, 1991.

[18]叶修松. 机载激光水深探测技术基础及数据处理方法研究[D]. 郑州: 信息工程大学, 2010.

YE Xiusong. Research on Principle and Data Processing Methods of Airborne Laser Bathymetric Technique[D].Zhengzhou: Information Engineering University, 2010.

[19]BURMAN H. Calibration and Orientation of Airborne Image and Laser Scanner Data Using GPS and INS[D]. Stockholm: Royal Institute of Technology, 2000.

[20]SKALOUD J, LICHTI D. Rigorous Approach to Bore-sight Self-calibration in Airborne Laser Scanning[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 61(1): 47-59.

[21]GUENTHER G C. Airborne Laser Hydrography: System Design and Performance Factors[R]. Rockville MD: National Oceanic and Atmospheric Administration, 1985.

[22]THOMAS R W L, GUENTHER G C. Water Surface Detection Strategy for an Airborne Laser Bathymeter[C]∥RICHARD W. Proceedings of SPIE 1302, Ocean Optics X. Orlando: International Society for Optics and Photonics, 1990: 597-611.

[23]GUENTHER G C, BROOKS M W, LAROCQUE P E. New Capabilities of the “SHOALS” Airborne Lidar Bathymeter[J]. Remote Sensing of Environment, 2000, 73(2): 247-255.

(责任编辑：张艳玲)

修回日期： 2016-01-07

First author： LI Kai(1992—)，male, postgraduate, majors in airborne laser bathymetry technology.

E-mail： likai_rs@163.com

Positioning Model and Accuracy Evaluation of Conical Scanning Airborne Laser Bathymetry System

LI Kai,ZHANG Yongsheng,TONG Xiaochong,SHEN Erhua

Institute of Survering and Mapping, Information Engineering University, Zhengzhou 450001, China

Abstract：Conical scanning airborne laser bathymetry system with fixed angle is selected as a research object to deduce the vector equation of laser in the prism, the atmosphere and the water from the internal structure of the laser rangefinder. Then the vector equation is combined with GPS/INS to deduce positioning model of foot laser point in mapping coordinates. The factors that influence the positioning accuracy of the airborne laser bathymetry system are fully considered and comprehensive accuracy evaluation model of conical scanning airborne laser bathymetry system is given with the use of error propagation law. System parameters, indicators which are widely used in the world are used to calculate the positioning accuracy of airborne laser bathymetry system. The main sources of error involved in positioning model are analyzed and discussed.

Key words：fixed angle conical scan; airborne laser bathymetry; positioning model; accuracy evaluation

第一作者简介：李凯(1992—)，男，硕士生，研究方向为机载激光测深技术。

收稿日期：2015-04-01

基金项目：国家自然科学基金(41201392);信息工程大学地理空间信息学院硕士学位论文创新创优基金(XS201502)

中图分类号：P225.2

文献标识码：A

文章编号：1001-1595(2016)04-0425-09

Foundation support： The National Natural Science Foundation of China (No. 41201392); Master Thesis Innovation Foundation of Geospatial Information Institute of Information Engineering University (No. XS201502)

引文格式：李凯，张永生，童晓冲，等.定角圆锥扫描式机载激光测深系统定位模型与精度评价[J].测绘学报，2016,45(4)：425-433. DOI:10.11947/j.AGCS.2016.20150161.

LI Kai, ZHANG Yongsheng, TONG Xiaochong, et al.Positioning Model and Accuracy Evaluation of Conical Scanning Airborne Laser Bathymetry System[J]. Acta Geodaetica et Cartographica Sinica,2016,45(4):425-433. DOI:10.11947/j.AGCS.2016.20150161.