On the Dynamical Behavior of Pest and it’s Predator Model∗
2016-05-16NIULinaMehbubaRehim
NIU Lina,Mehbuba Rehim
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
0 Introduction and model description
There has been great interest during the last few decades in dynamical characteristics of population models[1−3]and among these models,predator-prey systems play an important role in population dynamics.The dynamical relationship between predators and their preys has been an important topic in theoretical ecology since the famous Lotka-Volterra equation.The most crucial element in predator-prey models is the“predator functional response on prey population”,the function that describes the number of prey consumed per predator per unit time for given quantities(densities)of prey and predator.Various forms of functional responses have become the focus of considerable attention from time to time in ecological literature among which the most important and useful functional responses are Lotka-Volterra functional response(Holling type I functional response)and Holling type II functional response[2,3].
An organism which harms agriculture by means of feeding on crops or parasitizing livestock is known to us as pest.The term pest is used to refer not only to harmful animals but it also relates to all other harmful organisms,like fungi,bacteria,virus parasites,etc.It is also possible that an animal may be a pest in one case but beneficial or domesticated in another situation.But in this paper by the word‘pest’we mean those livelihood which are involved to the cause of the damages to the human populations directly or indirectly.In nature we are able to find some other types of species which predates those pests.For an example we may say that there are some birds,frog,etc.which used to catch the insects.These species may be treated as predator species to the pests as they predates the prey pests.Sometimes it is seen that the pest populations are affected by some diseases[4−7].In this case those disease affected pests are more vulnerable to the predators because they are easy to catch than the healthy one.Thus the parasite for the disease indirectly causes the reduction for the pests.According to the research works[8−10]on the dynamic of the interactions among crop,pest,disease and predators,T.K.Kar et al.[11]established and analysed the following eco-epidemiological model

In model(1),in the presence of disease,the total pest populations N are divided into two distinct classes,namely,susceptible pest populations,S,and infected pest populations,I.Pis the biomass for the predator population at that time t.In[11],authors assume that only susceptible pest(S)are capable of reproducing with logistic law,whereas the infected pest are unable to reproduce as mentioned by Hamilton et al.[12].Thus the infected individuals fail to contribute in the reproduction process for their inability to compete for resources.The mode of disease transmission follow the simple law of mass action and spread among the susceptible pest population only.The infected pest population does not recover or become immune.It is assumed that handling time for infected pests is negligible since they are more vulnerable for the predators,where as the predator needs sufficient handling time for the susceptible pest and these are incorporated using two different functional responses of Holling type I and II respectively.
In this article,motivated by the model(1),we develop a model for the interactions of susceptible pest and infected pest subject to attacks by a generalist predator,where“generalist”is defined such that the pest’s predator can survive in the absence of the pest prey.In addition,we suppose that speciesS,IandPsatisfy the following ecological assumptions:
Only the susceptible pest are capable of reproducing with logistic law,whereas the infected pest are unable to reproduce[12].
IntheabsenceofspeciesIandP,speciesSgrowsaccordingtoalogisticfunctionwithcarryingcapacityk1(k1>0),with an intrinsic growth rate constantr1(r1>0).
In the absence of pest,speciesPis a generalist predator,then it follows a logistic growth function with carrying capacityk2(k2>0),with an intrinsic growth rate constantr2(r2>0).
The interaction between susceptible pest and infected pest,susceptible pest and predator following Holling-Type I functional response and that of between infected pest and its predator following Holling-Type II functional response.Then based upon the assumptions above,a continuous time pest and its predator model with generalist predator can be described as follows:
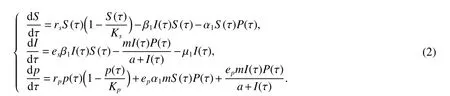
where β1is the force of infection between susceptible and infected pest populations,α1is the search rate of susceptible pest by its predator,mis the search rate of infected pest by its predator,µ1is the natural death rate of the infected pest,ei,i=s,pare the conversion factors and lastlyais the half saturation constant.All the above described parameters are assumed to be positive from the biological point of view.
The rest of this article is organized as follows:In Sect.2,we firs show positive and boundedness of the solution,and then sufficient conditions for the system of local stability of the boundary equilibria,persistence and extinction are obtained.Finally,all possible existence of interior equilibria be analysed.Some numerical simulations are given in section 3.
1 Mathematical analysis
For the convenience of mathematical analysis,we can simplify system(2)as(3)by letting:
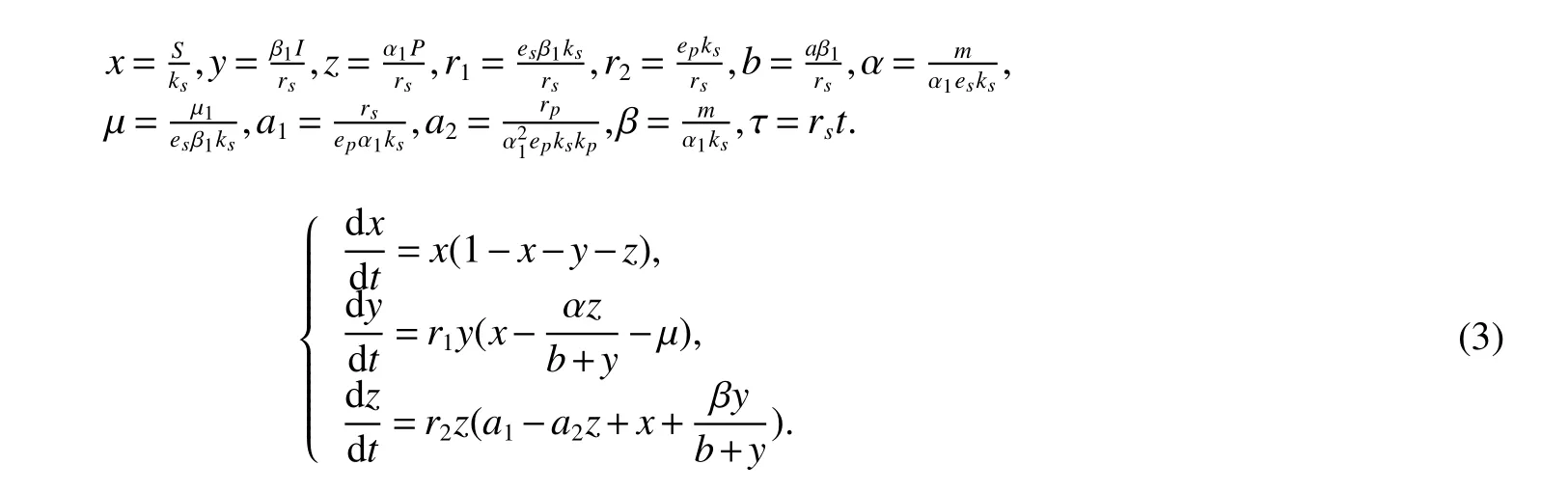
Then we can show the following lemma holds for system(3)
Lemma 1(Positive invariant and bounded)System(3)is positively invariant and bounded inR3+.Moreover,we have
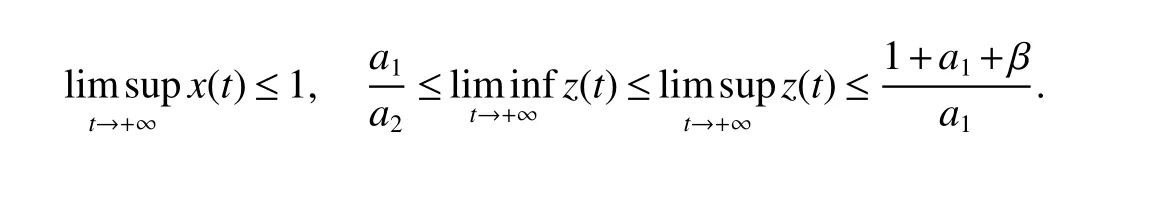
The proof Lemma 1 is simple,we omit it here.
1.1 Boundary equilibrium and their stability
Insystem(3)always has the boundary equilibriaE1(0,0,0),E2(1,0,0)andIfµ<1,then system(3)admits a boundary equilibriumE4(µ,1−µ,0).If<1,then there exists a boundary equilibriumBy evaluating the eigenvalues of their associated Jacobian matrices of system(3)at these equilibria,we are able to obtain the sufficient conditions of the local stability of these boundary equilibria and we state that in the following lemma:
Lemma 2For system(3)the following statement holds true:
(1)Boundary equilibriaE1(0,0,0),E2(1,0,0)andE4(µ,1−µ,0)(µ<1)are always unstable.
(2)If<1,then equilibriumis locally stable.
(3)If>1,thenis locally stable.
Remark 1From Lemma 2 we have that if equilibriumis locally stable,then system(3)does not have the equilibrium
1.2 Global dynamics:extinction and persistence
The subsystem of(3)that includes only speciesxandzcan be represented by the following equation:

The dynamical behavior of system(4)can be summarized as the following proposition:
Proposition 1The system(4)is globally stable atif and only ifa2≤a1while it is globally stable atif and only ifa2>a1.
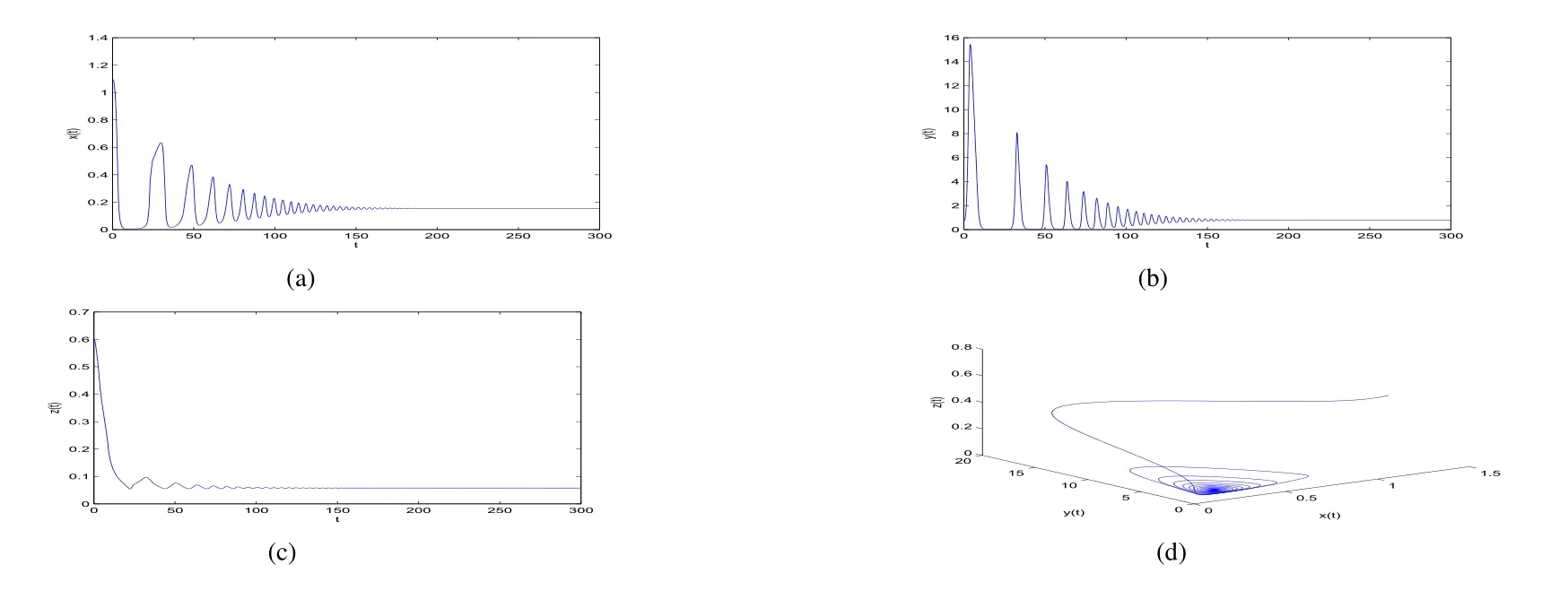
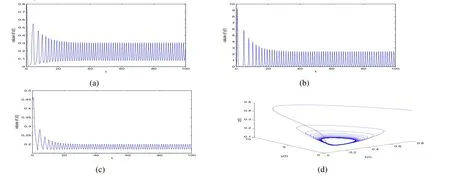
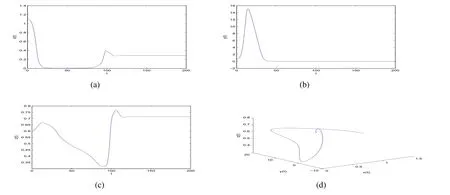
ProofIfa2 Therefore Ifa2>a1,then(4)has an interior equilibriumwhich is locally asymptotically stable while(0,0)andare saddle nodes.By Poincare-Bendixson Therom[13],the omega limit set of system(4)is either a fixed point or a limit cycle.Now define a scalar functionand let Then we have Therefore,according to Dulac‘s criterion[13],we can conclude that the trajectory of any initial condition taken inconvergies to an equilibrium point.Since the only locally stable equilibrium of(4)whena2>a1is the interior equilibrium pointtherefore,it must be global stable. In the case thata1=a2,(4)has equilibriumand other two unstable equilibria(0,0)and(1,0).Then according to Poincare-Bendixson Therom[13]again,we can conclude that all trajectories should converges tothusis global stable.The necessary conditions are easily derived from the local stability. Definition 1(persistence of single species)Speciesxsaid to be persistent infor system(3)if there exist positive constantsmandM,m Definition 2(persistence of a system)System(3)said to be permanent if there are positive constantsmandM,m holds for any solution of system(3)with conditionsx(0)>0,y(0)>0,z(0)>0. From Lemma 1,we know that specieszis persistent for any initial condition value taken inIn what follows,we shall show that the local stability ofindicate their global stability ifa1>a2. Theorem 1Specieszis persistent infor system(3)which is global stable atifa1>a2. ProofAssume thata1>a2for system(3),then from Lemma 1,for any ε>0 such that 1+ε Since infected pest are unable to reproduce and do not recover,if there is no susceptible pest,infected pest will extinct.Thus we have limt→∞y(t)=0.This implies that the limiting system of(3)isz'=r2z(a1−a2z),therefore,This indicates that system(3)is globally stable at Theorem 2For system(3),speciesxandzare persistent inIf,in addition,µ>1,equilibrium pointis globally stable.Similarly,speciesyandzare persistent inandµ< ProofAccording to Lemma 1,we can restrict the dynamics of system(3)on the compact setC=[0,M]×[0,M]×[m,M],wherem,Mare positive constants.Since specieszis persistence for system(3),thus sufficient conditions for the persistence of speciesxandzor the persistence of speciesyandzare equivalent to sufficient condition for the persistence ofxandy,respectively.The omega limit set of they−zsubsystem restricted onCisTherefore,according to Theorem 2.5 of Hutson[14],speciesxis persistent inif Sincey'=≤r1y(x−µ),thus,according to Lemma 1,speciesyof system(3)goes to extinct ifµ>1.Therefore,the limiting set system is thex−zsubsystem ifa1 Since persistence of speciesyrequires persistence of speciesx,i.e.,a1 Therefore,sufficient condition for the persistence of speciesandµ< FromTheorem2,wecanobtainsufficientconditionsforthepersistenceofthreespeciesbylookingatthesufficient conditions for the persistence of two species:the persistence of speciesyindicates that the persistence of three species since specieszis always persistent and speciesyderive from speciesx.Thus we have the following corollary for sufficient conditions of the persistence of the system(3). Corollary 1System(3)is pesistent ini.e.,three speciesx,y,zare all persistent inif the following inequalities hold From above argument we know that specieszor both speciesxandznever go to extinction.For the extinction of other species,from Theorem 1 and Theorem 2,we obtain the following corollary Corollary 2(Extinction of species)For system(3),the following state holds true: 1.If>1,then Speciesxgoes to extinction; 2.If µ>1 or>1,then speciesygoes to extinction; Remark 2From Theorem 1 and Theorem 2 we can conclude that the relative rates γi,i=1,2 do not affect species persistence.The persistence of system(3)are determined by the availability of outside resource,i.e.,a1anda2.The permanence of system(3)holds whenever speciesypersists. In this section,we explore the possible number of interior equilibria for system(3). Assume(x∗,y∗,z∗)is an interior equilibrium of system(3),then we have From(5)we get subject to This implies that where Obviously A is positive.However,the signs of B,C,D are not obvious.Now applying Descartes’rule of signs in Eq.(7)we obtain (i)ifB>0,C>0,D>0,then there is no change of sign,so there exists no positive real root of Eq.(7), (ii)ifB>0,C>0,D<0,orB>0,C<0,D<0 orB<0,C<0,D<0,then there exists only one positive root of Eq.(7), (iii)ifB>0,C<0,D>0 orB<0,C<0,D>0 orB<0,C>0,D>0,then there exists two or no positive roots of Eq.(7), (iv)ifB<0,C>0,D<0,then there exists three or one positive roots of Eq.(7). Therefore,ifD<0 there must exist at least one positive root of Eq.(7).Further,ify∗<1−µ,thenz∗>0,x∗>0.Thus,we have the following result. Theorem 3The sufficient conditions for existence of at least one non-trivial interior equilibriumE∗(x∗,y∗,z∗)of the system(3)areDin Eq.(7)must be negative andy∗<1−µ. Remark 3From Theorem 3 we know that ifD<0,then system(3)have at least one interior equilibrium.D<0 indicates thatµ In this section we give some numerical simulations regarding the permanence and stability of the system(3)around the interior equilibriumE∗and boundary equilibrium. Fig 1(a)-(c)Stable solution curves of system(3)for a2=4.5>1.99 with initial value.(d)Stable phase portrait of system(3)for a2=4.5>1.99.Equilibrium E∗(0.1538,0.7895,0.0579)is asymptotically stable.Here initial values are x(0)=1.1,y(0)=0.7,z(0)=0.6 Fig 2(a)-(c)Stable periodic solution curves of system(3)for a2=1.5<1.99 with initial value.(d)Stable periodic phase portraits of system(3)for a2=1.5<1.99.Here initial values are x(0)=0.4,y(0)=0.2,z(0)=0.45 For simulation let us taker1=25,r2=1,α=0.1,b=0.5,β=0.01,a1=0.1,µ=0.15.Our numerical simulations show that the interior equilibrium pointE∗is asymptotically stable for the values ofa2larger than value 0.564.Interior equilibrium pointE∗becomes unstable fora2lying between 0.564 and 1.99 and a limit cycle occurs.The periodic solution disappears ata2≈0.563 and the boundary equilibriumE5becomes asymptotically stable for the values ofa2∈(0.1,0.564).Fora2=4.5,the interior equilibrium pointE∗(0.1538,0.7895,0.0579)is asymptotically stable.This phenomenon is presented in Fig 1(a)-(d)in terms of solution curves and phase space portrait respectively.Fora2=1.5,there is limit cycle occurs and it is presented in Fig 2(a)-(d).The Hopf bifurcation occurs ata2≈0.564.Fora2=0.51,and the boundary equilibriumE5(0.2859,0,0.7148)becomes asymptotically stable.This phenomenon is presented in Fig 3(a)-(d). We see that all the conditions for the permanence of the system(3)and existence of interior equilibrium hold. Fig 3(a)-(c)Time series of a converging solution of system(3)for a2=0.51<0.564 with initial value.(d)Stable phase portraits for a2=0.51<0.564.For a2=0.51<0.564,periodic solution disappears and boundary equilibrium E5(0.2859,0,0.7148)becomes stable.Here initial values are x(0)=0.4,y(0)=0.2,z(0)=0.45 References: [1]Hale JK.Theory of Functional Differential Equations[M].New York:Springer,1977. [2]Kot M.Elements of Mathematical Ecology[M].Cambridge:Cambridge University Press,2001. [3]Murray JD.Mathematical Biology[M].New York:Springer,1993. [4]Bhattacharyya S,Bhattacharya DK.Pest control through viral disease:mathematical modeling and analysis[J].J Theor Biol,2006,238:177-196. [5]Ghosh S,Bhattacharyya S,Bhattachary DK.The role of viral infection in pest control:a mathematical study[J].Bull Math Biol,2007,69:2649-2691. [6]Wang X,Tao Y,Song X.Analysis of pest-epidemic model by releasing diseased pest with impulsive transmission[J].Nonlinear Dyn,2011,65:175-185. [7]Tan Y,Chen L.Modelling approach for biological control of insect pest by releasing infected pest[J].Chaos Solitons and Fractals,2009,39:304-315. [8]Boethel D J.Eikenbary D.Interactions of Plant Resistence and Parasitoids and Predator of Insects[M].UK:Wiley Chinchester,1986. [9]DeBach P.Biological Control of Insect Pests and Weeds[M].London:Chapman and Hall,1964. [10]Burges HD,Hussey NW.Microbial Control of Insects and Mites[M].New York:Academic Press,1971. [11]Kar TK,Abhijit Ghorai,Soovoojeet Jana.Dynamics of pest and its predator model with disease in the pest and optimal use of pesticide[J].J Theor Biol,2012,310:187-198. [12]Hamilton WD,Axelrod R,Tanese R.Sexual reproduction as an adaptation to resist parasites(a review)[J].Proc Natl Acad Sci,United States of America,1990,87:3566-3573. [13]Guckenheimer J.Holmes P Nonlinear oscillations,dynamical systems,and bifurcations of vector fields[M].Berlin:Springer,1983. [14]Hutson V.A theorem on average Liapunov functions[J].Monatshefte fur Mathematik,1984,98:267-275.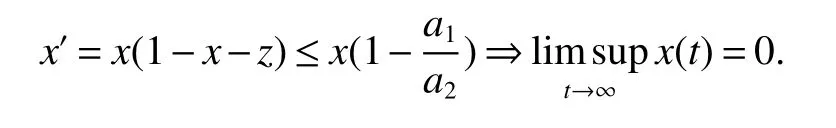
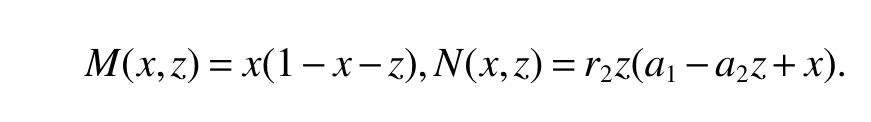
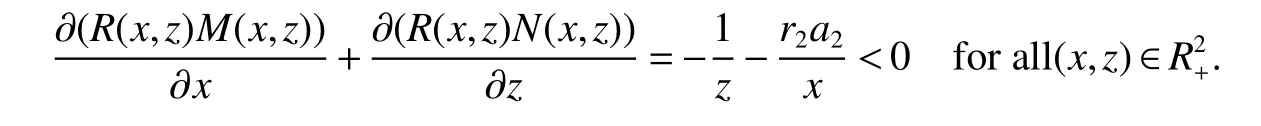
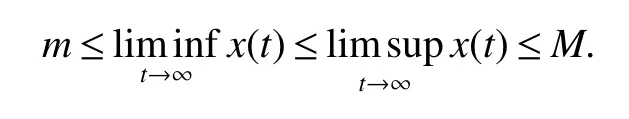
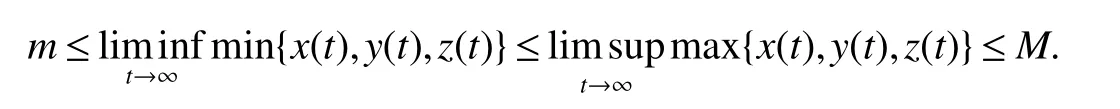
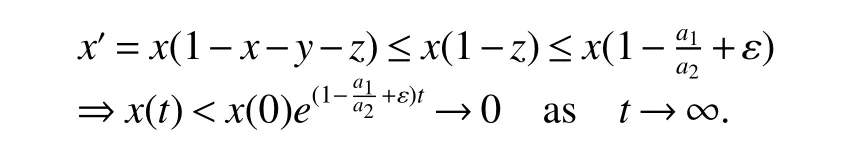

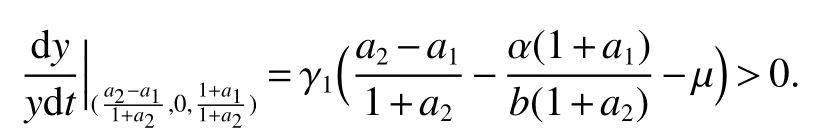
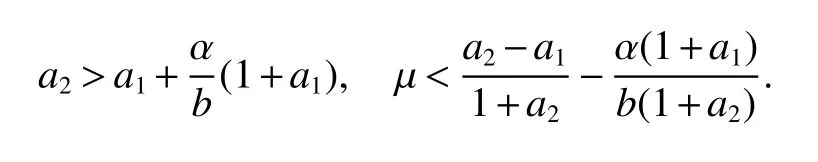
1.3 Existence of interior equilibrium,multiple atractors

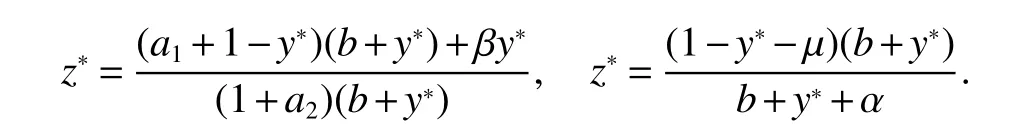



2 Numerical simulation of the system behavior
杂志排行
新疆大学学报(自然科学版)(中英文)的其它文章
- The Absolute Ruin Risk Model with Constant Interest Investment and Linear Threshold Dividend Strategy∗
- 煤基活性炭的氧化改性及其对Cd2+的吸附性能∗
- 细菌诱导光滑鳖甲幼虫抑制差减cDNA文库的构建与分析∗
- 资源型产业与制造业集聚特征与影响因素异同分析∗
- Distance Signless Laplacian Integral Complete R-partite Graphs∗
- Finite-time Stability of Continuous-time Systems with Time-varying Delays∗
