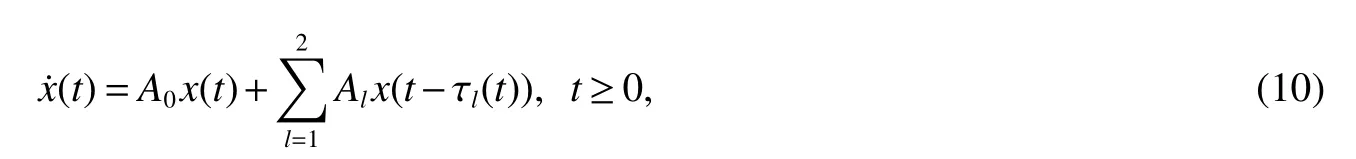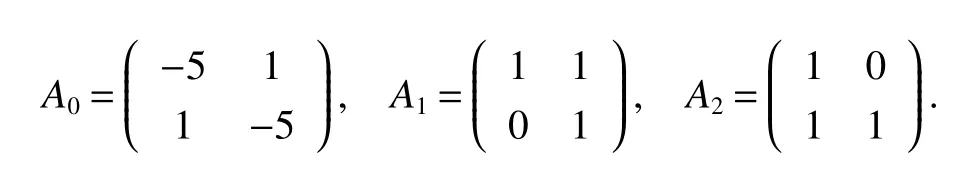Finite-time Stability of Continuous-time Systems with Time-varying Delays∗
2016-05-16LIYingkeTENGZhidongNerbekAizmah
LI Yingke,TENG Zhidong,Nerbek Aizmah
(1.College of Mathematics and Physics,Xinjiang Agriculture University,Urumqi xinjiang 830052,China;2.College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
0 Introduction
In the past decades,the concept of Lyapunov asymptotic stability(LS)has been dominating in the field of theory of system stability[1–4].From a practical point of view,however,it is more valuable that the dynamic behavior of the system is realized in finite time rather than infinite time,this is so called finite-time stability(FTS)(or short-time stability)[5].FTS of systems and stabilization of them have been extensively studied recently[6–12].General speaking,given a bound on the initial condition,a system is said FTS if its state trajectories dose not exceed a certain threshold during a pre-proposed time interval[5].
Various results to check FTS as well as to solve the corresponding design problems have been provided for delay systems[5–7],switching and impulsive systems[8],linear system recently[9–12],and stochastic systems[12].Bhat and Bernstein obtained conditions for FTS of an autonomous systems in terms of scalar differential inequalities by using Lyapunov and converse Lyapunov[9].By applying different Lyapunov-Krasovskii functionals,some sufficient conditions for FTS of linear discrete-time with time-varying delay were obtained in the form of inequalities[11].Currently,Liu and Yu[1,2]analyzed continuous time positive systems with time-varying delays and discrete positive systems with bounded time-varying delays,the conditions on system LS are described by Hurwitz matrix or Schur matrix,respectively.The main object of this paper is to show sufficient condition of FTS for positive systems with time-dependent delays.
The paper is organized as follows:model description and some preliminary results are introduced in Section 2.The main results of this paper,namely,sufficient conditions for FTS of time-dependent delays systems are presented in Section 3.In Section 4,the effectiveness and feasibility of the proposed condition are shown by numerical examples.
NotationsFor the given positive integermandn,we denotem0:={0,1,···,m},={1,2,···,n}.R+=[0,∞),Rnrepresents then−dimensional space with the normstands for the set of realm×n−matrices.Foru=(ui),v=(vi)inRn,u≤vif and only ifui≤vi;u?vif and only ifLete=(1,1,···,1)T∈Rn.
1 Problem statement and Preliminaries
Let us consider the following time-varying delays system:
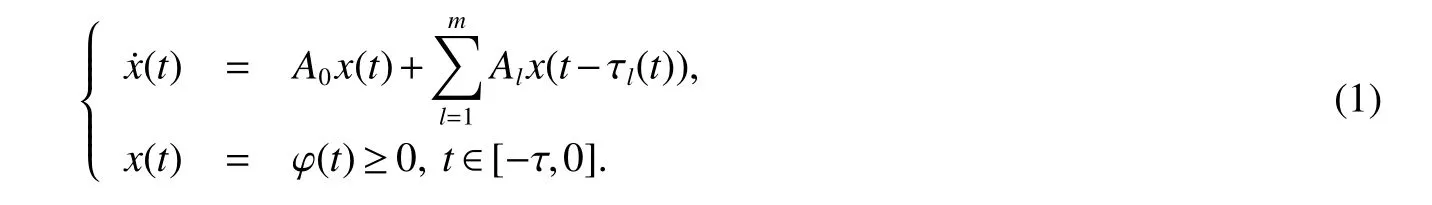
wherex(t)∈Rnis the state variable,are system matrices.Delay τl(t)is assumed to be bounded and continuous with respect tot,and satisfies
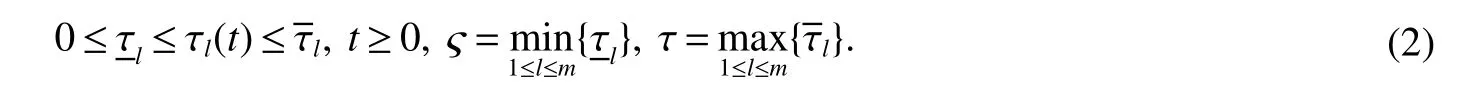
(t)=(ϕi(t))∈C([−τ,0],Rn)is the initial function,whereC([−τ,0],Rn)denotes the Banach space of all continuous functions mapping the interval[−τ,0]intoWe usex(t)to denote the
solutionx(t,ϕ)in the following if it does not make any confusion.
Definition 1For a given timeT>0 and positive numbersd1 We make the following preparation for introducing Metzler matrix.For any matrixM∈Rn×n,the spectrum ofMis denoted by σ(M)={λ:det(λIn−M)=0}and the spectral abscissa ofMis denoted byr(M)=max{Reλ:λ ∈σ(M)}.An×n−matrix is called Metzler matrix if all of f-diagonal elements ofMare non-negative.We quote here some properties of Metzler matrix[5]. Lemma 1[5]LetM∈Rn×nbe a Metzler matrix.The following statements are equivalent (i)r(M)<0; (ii)M is non-singular andM−1?0; (iii)There exists 0?ξ∈Rnsuch thatMξ?0; (iv)for any 0?b∈Rn,there existsx∈Rn+such thatMx+b=0; (v)There exists 0?ξ∈Rnsuch thatMTξ?0; (vi)For anyx∈Rn+{0},the row vectorxTMhas at least one negative entry. We make assumptions on the system matrices in(1)as follows: Let Mα=where α≥0,there exist Metzler matrixes such that Theorem 1For givenT>0 andd2>d1>0,if(H1)and(H2)hold,assume there exist α ≥0,λ1>0,λ2>0,e=(1,1,···,1)T∈Rnand ξ∈Rnsatisfying Then system(1)is FTS with respect to(d1,d2,T). ProofFor α>0,let ξ∈Rnsatisfied the first inequality in(3),then we have and hence Firstly,for anyt≥0 andwe obtain the Dini upper-right derivative along system(1) Secondly,define the functionsui(t)as follows Obviously,for allandt≥−τ,we have Thus,it follows from(4),(6)and(7)that Therefore,from(8),we have Next,we will prove that|xi(t)|≤ui(t),for anyt∈[0,T].Let ηi(t)=|xi(t)|−ui(t),t≥ −τ.For allt∈[−τ,0],we havewhich is that ηi(t)≤0 for allt∈[−τ,0]Assume that there exists ani0∈nandt0∈(0,T]such that ηi0(t0)=0,ηi0(t)>0,t∈(t0,t0+θ)for some θ>0 and ηi(t)≤0 for alltHenceD+ηi0(t0)>0.On the other hand,by(5)and(9),for allt∈[0,t0),we get henceD+ηi0(t0)≤0,which is a contradiction.This means that ηi(t)≤0 for allt>We easily obtainTherefore,for allt∈[0,T],if kϕk∞≤d1, According to Definition 1,system(1)is FTS with respect to(d1,d2,T).This completes the proof. Remark 1From Lemma 1 and the first inequality in(3),we ascertain thatMαis a set of Metzler matrix. Remark 2It is easily confirmed that,if the first inequality in(3)is satisfied with α=0,then system(1)is exponentially stable in the sense of Lyapunov[3,5].Furthermore,in this case system(1)is FTS with respect to(d1,d2,T)for any 0 Let us consider the following system where and τ1(t)=|sint|,τ2(t)=|cost|.We easily obtain that system(10)satis fi ed(H1)and(H2)for allT>0.For simpli fication,let A0=A0,A1=A1,A2=A2.It is noted that system(10)does not satisfy the asymptotically stable condition proposed inLemma4[1]when set λ=(1,1)T.However,Mα=A0−αIsatis fi es the fi rst inequalities in(3)for any α>0 and its solution η=(η1,η2)T∈R2is defined byIf we setd1=0.7,d2=1 and then system(10)is FTS with respect to(d1,d2,T)for any time 0 Fig 1 Time sires of xi(t)in(10)with initial values xi(0)=0.2+0.1k,k=−5,−4,···,5,i=1,2 References: [1]Liu X,Yu W,Wang L.Stability analysis for continuous-time positive systems with time-varying delays[J].IEEE Trans Automat Contr,2010,55(4):1024-1028. [2]Liu X,Yu W,Wang L.Stability analysis of positive system with bounded time varying delays[J].IEEE Trans Sircuits Syst II Exp Briefs,2009,55(7):600-604. [3]Xu J,Sun J.Finite-time stability of nonlinear switched impulsive systems[J].Inter J Syst Sci,2013,44(5):889-895. [4]Ngoc P.On exponential stability of nonlinear differential systems with time-varying delay[J].Appl Math Lett,2012,25:1208-1213. [5]Kamenkov G.On stability of motion over a finite interval of time[J].J Appl Math Mech USSR,1953,17:529–540. [6]Yang R,Wang Y.Finite-time syability and stabilization of a class of nonlinear time-delay system[J].SIAM J Control Optim,2012,50(5):3113-3131. [7]Hien L.An explicit criterion for finite-time stability of linear nonautonomous systems with delays[J].Appl Math Lett,2014,30:12-18. [8]Amato F,Tommasi D,Pironti A.Necessary and sufficient conditions for finiti-time stability impulsive dynamical linear systems[J].Automatica,2013,49:2546-2550. [9]Bhat S,Bernstein D.Finite-time stability of continous autonomous systems[J].SIAM J Cont Optim,2000,38(3):751-766. [10]Zuo Z,Li H,Wang Y.New criterion for finite-time stability of linear discrete-time systems with time-varying delay[J].J Franklin Inst,2013,350:2745-2756. [11]Stojanovic S,Debeljkovic D,Antic D.The applicatin of different Lyapunov-like functionals and some norm approximatations of the delayed states for finite-time stability analysis of linear discrete time-delay systems[J].J Franklin Inst,2014,3:3914-3931. [12]Chen W,Jiao L.Finite-time stability theorem of stochastic nonlinear systems[J].Automatica,2010,46:2015-2018.
2 Main results

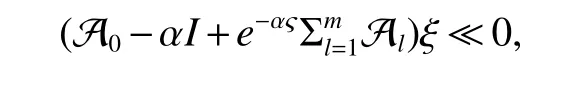
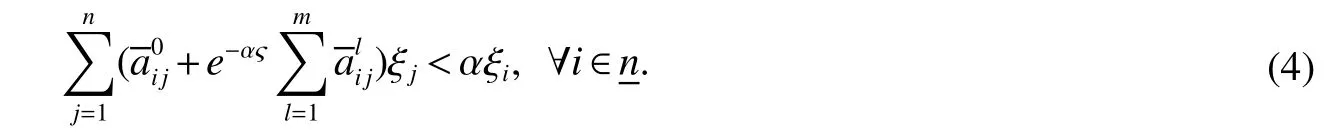
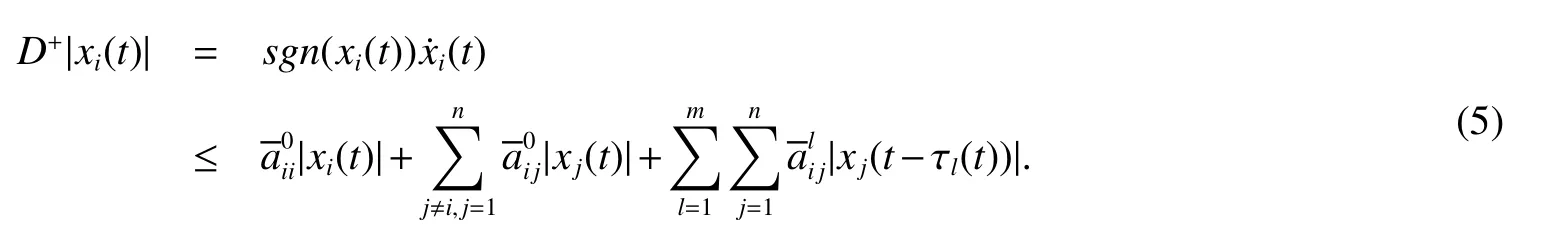
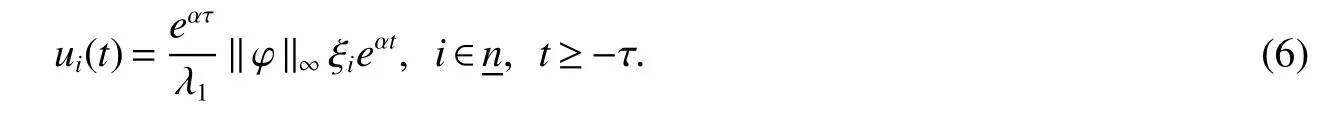
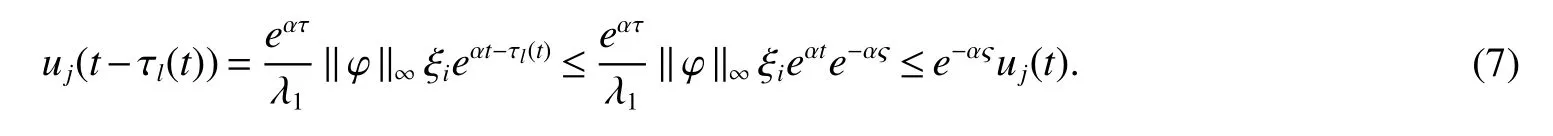
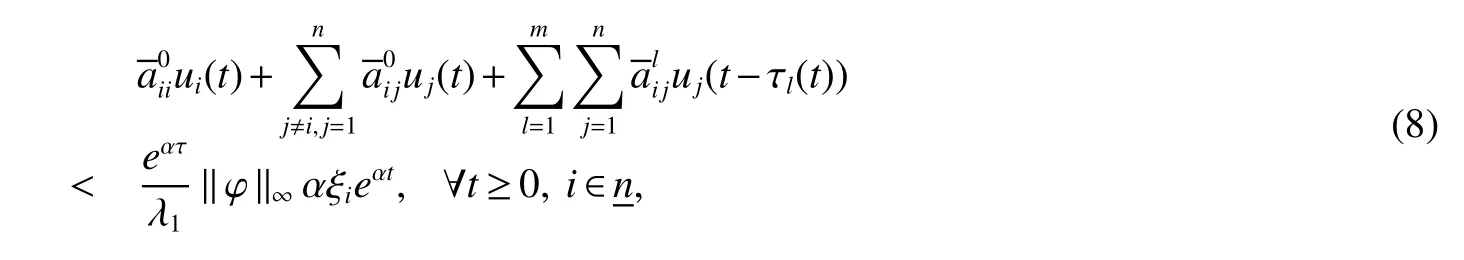
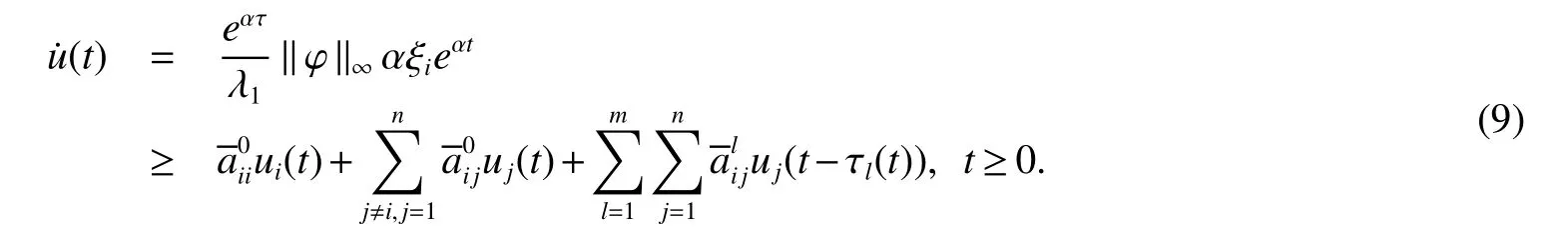
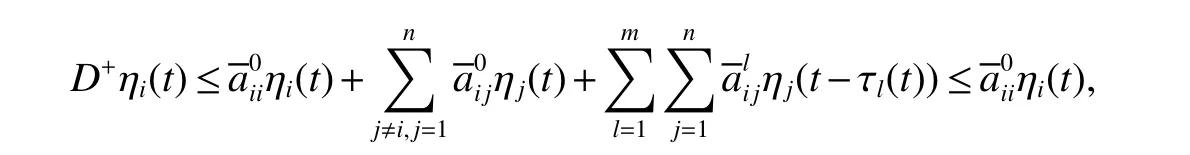
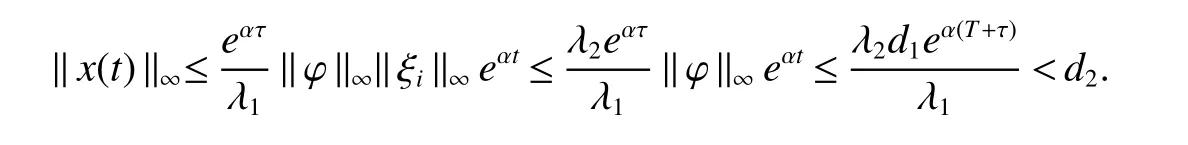
3 A numerical example