基于模糊决策理论的水资源优化配置方案评估探析
2016-05-15马桂英
马桂英
(新疆克孜尔水库管理局新疆拜城842000)
基于模糊决策理论的水资源优化配置方案评估探析
马桂英
(新疆克孜尔水库管理局新疆拜城842000)
本文构建了基于模糊决策理论的水资源优化配置方案评估模型,通过分析流域的水资源现状、水资源利用效率、区域防洪水平以及经济社会等方面的指标优度数值,从而优选最佳的水资源配置方案。实例表明,该模型可有效降低评估优选过程中的主观因素,方案评估结果客观可靠,可为相关案例提供参考。
模糊决策理论;层次分析法;水资源配置;方案评估
1 引言
水资源优化配置方案旨在充分考虑区域水资源配置现状的基础上,依据合理高效、公平的原则,由经济、社会以及生态环境等角度出发,综合分析区域水资源的不同作用与属性。同时对该区域水资源配置在生态环境、生活以及生产中的配置合理性以及满足程度进行探析,从而实现评估该区域规划配置与现状配置条件下的水资源综合效益值,进而判别该水资源配置方案的优劣程度,阐明其与规划水平年水资源配置标准的变化趋势合理程度[1]。近年来,多目标评估方法在水资源优化配置方案优选中应用广泛,层次分析法因其可将主观判别与抽象思维数量化与规范化,从而使得评估过程的计算简洁明了,并在很大程度上降低了不确定要素的影响程度,强化了决策思维的一致性[2]。鉴此,本文通过数量化新疆渭干河流域水资源优化配置方案中各项指标,从而探究模糊决策理论在水资源配置方案评估中的适用性。
2 模糊决策理论层次分析模型构建
2.1 水资源优化配置评估指标体系建立
可根据被评估的水资源优化配置方案来选定各评估层次的准则要素,从而构建评估指标体系,并运用层次分析法来为各评估体系指标赋值权重[3]。采用专家咨询法对各层级指标实施客观评判,依据1~9标度法来为各评估指标间的重要性程度定量赋值[4]。同时,结合专家咨询意见建立判别矩阵,并进行一致性水平检验。可采取方根法求得各指标的相对权重值E,计算如下:
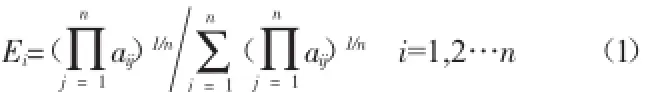
式中,aij表示判别矩阵A各要素;n表示矩阵的阶数。
2.2 模糊决策模型构建
可通过模糊一致性矩阵来优选水资源配置方案,组要包括如下步骤:
(1)构建优先级别关系矩阵Ak=(rijk)m×m,(k=1,2,…,n)其中,(rijk)m×m应满足如式2所示条件[5],
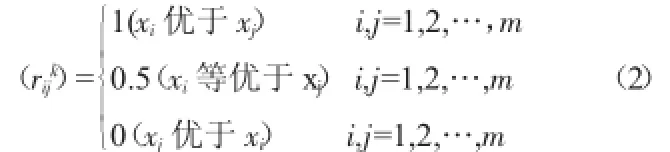
(2)可将上述矩阵Ak转化为模糊一致性矩阵[6],如式(3)所示,

(3)依据方根法可求得水资源优化配置方案Ai相对要素rk的优度数值vik,具体可由式4计算[7],

(4)依据层次分析法可求得各层级的指标所属权重值[8],从而可计算水资源配置各方案的综合优度数值Vi,具体计算如式5所示,
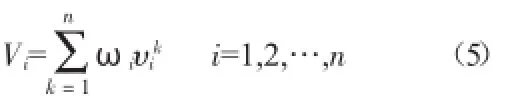
式中,ωi表示第i个指标要素的权重值。其中,Vi值越大则表示该水资源配置方案越优秀。
3 模型实例应用与分析
以新疆渭干河流域为例,采用上述构建的评估模型优选该流域水资源配置方案。经现场调研及历史资料分析可知,该流域水资源时空分配呈现明显的春旱夏涝趋势,流域农业灌溉方式相对落后,部分区域土壤盐碱化问题突出,农作物产量相对较低。新疆渭干河流域属于典型的大陆性干旱气候区,因此,选取该流域实施水资源优化配置方案的优选探析具有典型的代表性意义。
在充分考虑新疆渭干河流域气候条件以及地理环境因素的前提下,依据该地区水资源分配实际情况,将经济、社会以及生态要素融入该流域的水资源综合配置规划中,从而提出如下水资源配置方案:①在该地区修建地表拦蓄水库,此作为第一种方案;②在修筑地表拦蓄水库的同时,加大区域地下水的开采力度,此作为第二种方案;③在修筑地表拦蓄水库、开采地下水的同时,兴建水源调蓄池,此作为第三种方案。针对上述方案的评估指标体系可如表1所示。
3.1 层次指标权重确定
依据1~9标度值法以及专家咨询法,对新疆渭干河流域的水资源配置方案各层指标实施对比,在通过一致性水平检验以及矩阵运算之后,可求得该流域水资源评估体系各层级指标的权重值。该流域水资源优化配置方案各层级指标权重值如表2所示。
3.2 优先关系矩阵构建
通过测定及对比各水资源配置方案层级指标,可构建涵盖新疆渭干河流域水质现状、水量现状、地下水变化现状、水资源损耗率、地表水使用效率、防洪水平、工程耗资以及单位水量开采成本在内的指标评估矩阵Ak(k=1,2,…,8),将矩阵Ak转化为模糊矩阵Bk,具体如下表示:

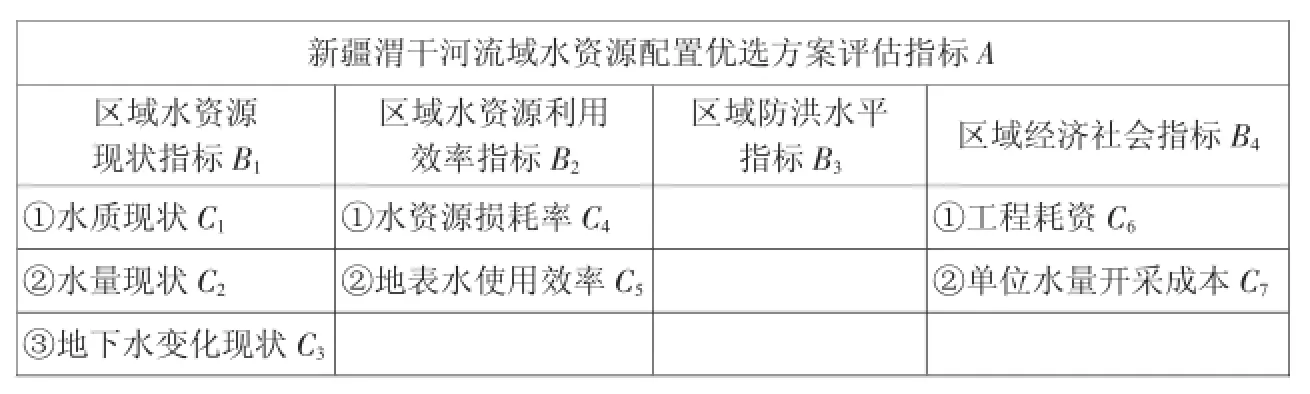
表1 水资源配置方案评估指标体系
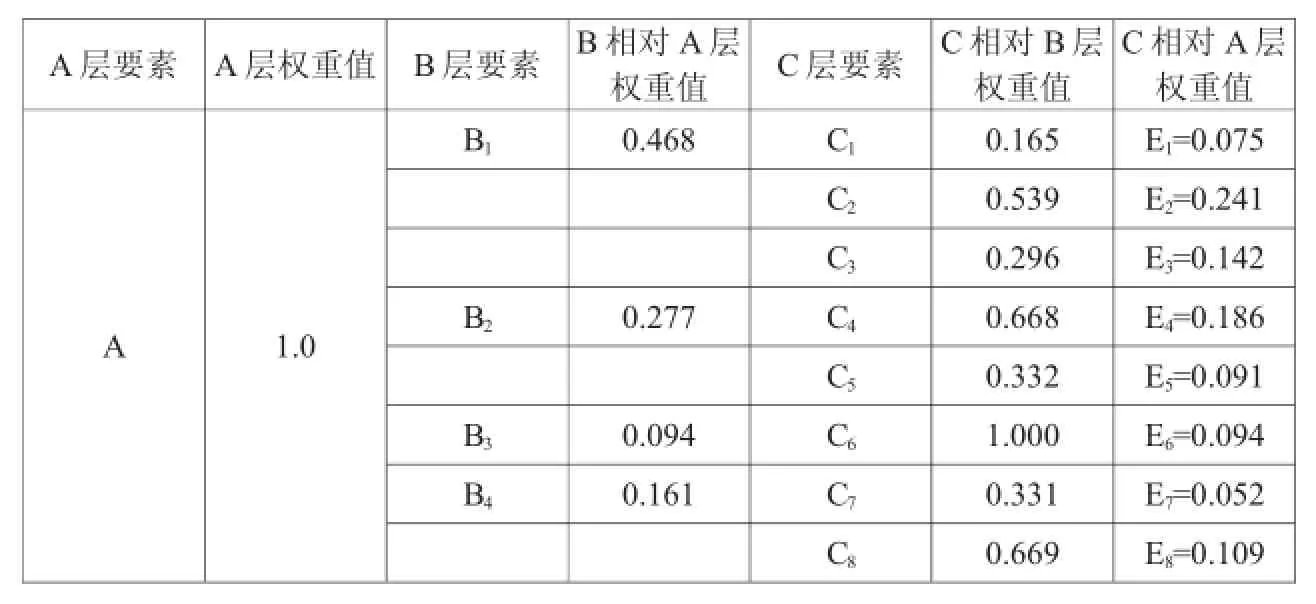
表2 流域水资源优化配置方案各层级指标权重值
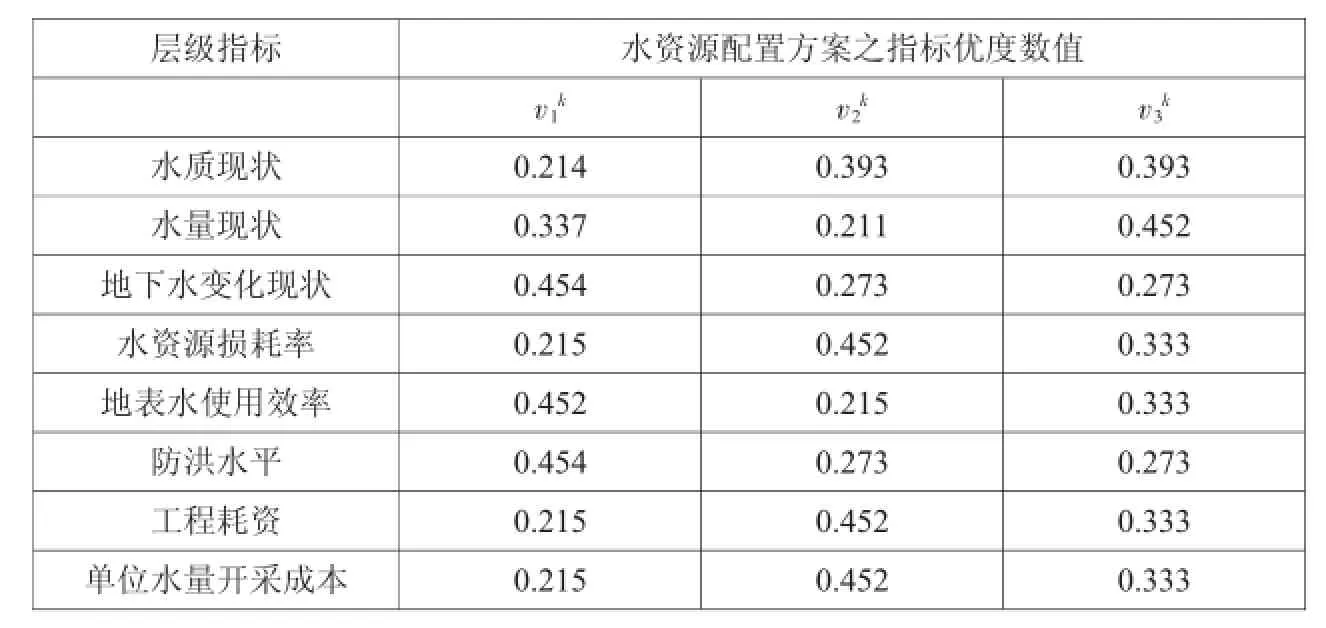
表3 水资源配置方案指标优度数值
3.3 水资源配置方案优选评估
依据式4可求得水资源配置各方案指标的优度数值,计算结果如表3所示。
3.4 水资源配置方案评估结果
依据表3计算所得的水资源配置方案评估指标优度数值可知,采用方案三在水质及水量指标方面明显优于方案二级方案一,而方案三的其余各项评估指标的优度数值相较于其余两方案均属于折中水平。
依据式5以及表2中指标优度数值数据,可计算方案一、方案二以及方案三的综合优度数值分别为:0.319,0.322以及0.359,V3=0.359>V2>V1,即V3在加权后的综合优度数值最大,说明方案三优于方案一与方案二,方案三即为该流域水资源配置的最优化方案。究其原因,方案三在修筑地表拦蓄水库、开采地下水的同时,通过兴建水资源调蓄池来协助地表拦蓄水库调配水源,从而实现了区域地表水与地下水资源的科学统一调配使用。针对方案一而言,修建单一的地表拦蓄水库将占用大面积土地资源,因此其工程耗资过大。对于方案二而言,针对区域地下水资源的过度开采,可能引发区域地下水降落漏斗,对流域的地质条件以及生态环境造成负面影响。综合而言,第三种水资源配置方案,即在修筑地表拦蓄水库、开采地下水的同时,兴建水源调蓄池,无论在对流域生态环境的维护以及方案实施的可行性、投资规模适度性方面均优于其余两种方案。
通过上述计算与论证分析可知,采取基于模糊决策理论的层次分析模型计算上述三种水资源配置方案,计算结果同论证分析结论一致,说明该方法与模型适用于水资源配置方案的论证优选。
4 结语
通过建立新疆渭干河流域水资源配置方案优选评估指标体系,采取构建的模糊决策层次分析模型评估流域的水资源配置方案,并将计算结果同综合论证分析结论比较,结果说明基于模糊理论的层次分析模型在水资源优化配置方案的优选中具有较强的适用性。该模型具有较好的严密性且计算过程简洁明了,有效克服了方案比选的主观影响,对区域水资源优化配置方案的优选具有一定借鉴价值。陕西水利
[1]李新华.落实最严格的水资源管理制度全面推进水资源配置、节约与保护[J].陕西水利,2010,(2):10-11.
[2]娄帅,王慧敏,牛文娟,许叶军.基于区间直觉模糊集的水资源配置群决策研究[J].长江流域资源与环境,2014,(3):319-327.
[3]杨志,王修内.盐环定扬黄工程宁夏受水区水资源配置研究[J].陕西水利,2010,(5): 133-134.
[4]梁士奎,左其亭.基于人水和谐和“三条红线”的水资源配置研究[J].水利水电技术,2013,(7):1-4.
[5]冯缠利,贺随成.陕北榆林能源化工基地水资源配置及供水网络研究[J].陕西水利,2012,(6):61-62.
[6]叶健,刘洪波,闫静静.不确定性模糊多目标模型在生态城市水资源配置中的应用[J].环境科学学报,2012,(4):1001-1007.
[7]陈博.可持续水资源管理中的水资源危机管理[J].陕西水利,2012,(6):29-30.
[8]万新宇,郑永路.水资源配置方案多层次可变模糊决策[J].水力发电,2013,(11):11-15.
(责任编辑:畅妮)

TV213.4
A
