通用型高速LDPC码编码器设计与FPGA实现
2016-05-14陈全坤杨奇李二保雷菁
陈全坤 杨奇 李二保 雷菁

摘要:随着高速数据传输业务的快速发展,人们对信息传输的质量和速率要求越来越高,高速LDPC码编译码器在通信系统中的应用需求更加强烈。在节约硬件资源的前提下,为最大限度的降低编码时延、提高编码器速率,本文从编码算法的通用性出发,将一致校验矩阵通过行列置换和高斯消元,使每个校验位的运算只与预处理后矩阵的对应行相关,具备了可以灵活并行处理的结构。在编码器的硬件设计上,本文提出了一种校验位并行分步运算的编码器架构,通过同时计算所有校验位,分步处理单个校验位,有效地降低了硬件实现复杂度,缩短了关键路径时延,提高了编码速率。实现结果表明,本文设计和实现的编码器工作时钟频率可以达到250MHz,相应的吞吐量为14Gbit/s。
关键词:通用型 LDPC码 高速编码器
中图分类号:TP3 TN4 文献标识码:A 文章编号:1007-9416(2016)05-0000-00
1 引言
低密度奇偶校验码(Low-dentisy Check Codes,LDPC码)是一种线性分组码,由Gallager博士于1963年在其博士论文中首次提出[1]。LDPC码校验矩阵具有稀疏特性,不仅描述简单、编译码复杂度比较低,而且错误平台较低,编译码可以实现硬件并行处理,在现行通信标准中得到了广泛应用。
人们对LDPC码的批评主要集中在高编码复杂度上[2],如何实现快速编码一直是LDPC码的一个研究热点。现行的编码方案有基于生成矩阵的编码算法和基于校验矩阵的编码算法两大类,前者是利用稀疏校验矩阵的特定结构,对校验矩阵进行预处理,求出生成矩阵后编码,而后者是利用校验矩阵直接进行编码。
本文立足工程实践的需求,采取高斯消元编码算法,设计出了资源占用较少、并行度高且算法灵活、关键路径时延低、布线简单的编码器结构,实现了编码速率的极大提高。
2 常用编码算法介绍与分析
对于一个LDPC码,设码字空间为C,校验位用P表示,信息位用S表示,则其码长为n,信息位个数为k,校验位个数为,由奇偶校验矩阵H唯一确定。校验矩阵H的每一行对应一个校验方程,每一列对应码字中的一个比特。编码时,可以先得到生成矩阵,再由生成矩阵与信息序列S的线性关系式求得码字:
2.1 基于LU分解的编码[3]
将校验矩阵H分为两部分,其中A为m阶的方阵。如果A可以通过行列变化和高斯消元,分解成为LU两部分(L为下三角矩阵,U为上三角矩阵),同时引入中间变量y,即可由L矩阵迭代得到中间向量y,再由U矩阵迭代得到校验序列P。这种算法的优点是运算复杂度与码长成线性关系;缺点是预处理时需要寻找优良的分解方法以保持矩阵的稀疏性,前后迭代运算时延较大。
2.2 基于近似下三角矩阵的编码
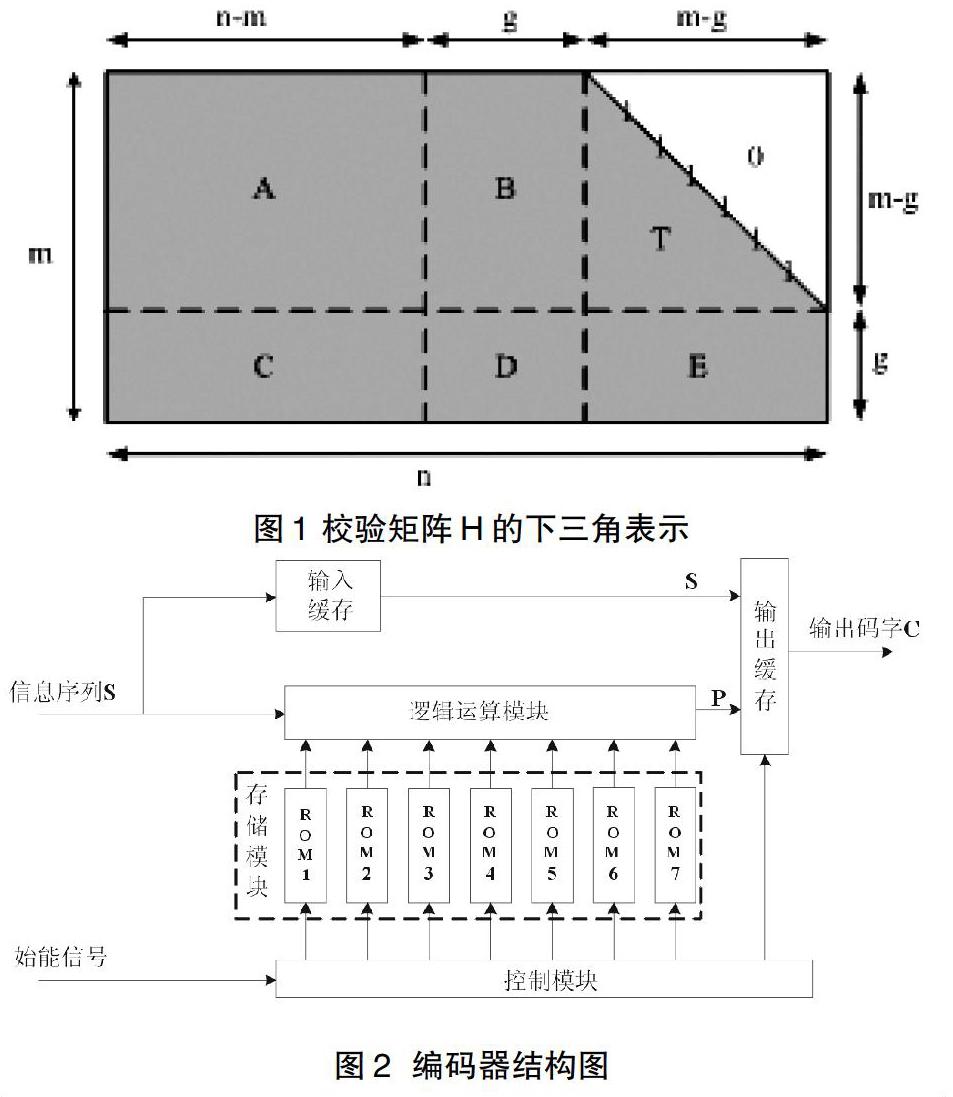
只对校验矩阵H进行行列置换,转化为具有近似下三角的结构[4](图1),其中H中剩下的行称为近似表示的间隙。
高斯消元清除E,同时将码字C写成,其中为前个校验位,为后个校验位,则有:
展开后,即可得出、的计算公式。该算法优点是,如果可以将g控制在较小范围内,复杂度与码长呈线性关系;缺点是重新排列矩阵实现较为复杂,且矩阵求逆复杂度较高,需要特定结构的校验矩阵以降低复杂度。
2.3 基于QC-LDPC码的编码
有学者提出了校验矩阵具有一定简单编码结构的准循环LDPC码[5],其校验矩阵被分割成若干个小的方阵,每个方阵由循环置换矩阵或全0矩阵构成。该码校验矩阵H和生成矩阵G都具有准循环结构,可以釆用移位寄存器进行存储,节约了硬件资源。
此外,在准循环 LDPC 码的基础上附加约束,使其具有更加方便进行处理的结构,也可以实现有效编码。这些方法的优点是编码复杂度进一步降低,不足之处是对校验矩阵具有更加特殊的要求,对一般LDPC码、特别是随机构造的LDPC码不具备通用性。
2.4 基于优化的高斯消元编码算法
上述编码算法都对编码复杂度进行了一定优化,但同时也有很大的局限性,一方面对LDPC码矩阵结构有特定的要求,通用性不强,另一方面硬件电路的设计也较为复杂,带来一定延时。因此,本文提出了一种基于优化的高斯消元的编码算法。
在消元过程中,少数列变换对生成码字的顺序有一定影响,计算出校验位后,根据变换顺序重新调整序列,即可得出正确的码字。这样,求解校验位的过程只与预处理后的校验矩阵中对应的行相关,便于实现行间高度并行的运算。这种编码方法的不足是破坏了校验矩阵的稀疏性;优点是通用性强,对于各种类型的LDPC码的校验矩阵都可以处理,并且在硬件实现上并行度高、时延小,布线较为简单,存储资源的占用也可以接受。
3 编码器硬件结构设计
以上分析了几种常用的编码方法,并对基于优化的高斯消元编码算法进行了介绍。本文以(4480,3920)LDPC码为例,基于优化的高斯消元编码方案,设计了一种校验位并行分步运算的编码器结构,如图2所示。
图2中,ROM1至ROM7表示7个ROM存储块,用来存储预处理后的校验矩阵。
工作流程可以描述为:每个时钟周期并行输入56个信息位,分别被传递给输入缓存模块与逻辑运算模块;同时,从7个ROM块中读取出矩阵的560行、56列元素,并送入逻辑运算模块;逻辑运算模块接收到两类数据后,开始执行校验位运算。此过程重复执行70个时钟周期后,逻辑运算模块计算出560个检验位,输送至输出缓存模块;此时,输入缓存模块恰好将缓存的3920个信息位传递给输出缓存模块;560个校验位和3920个信息位经输出缓存模块重新排序后,转化成 64路并行输出。
3.1逻辑运算电路设计
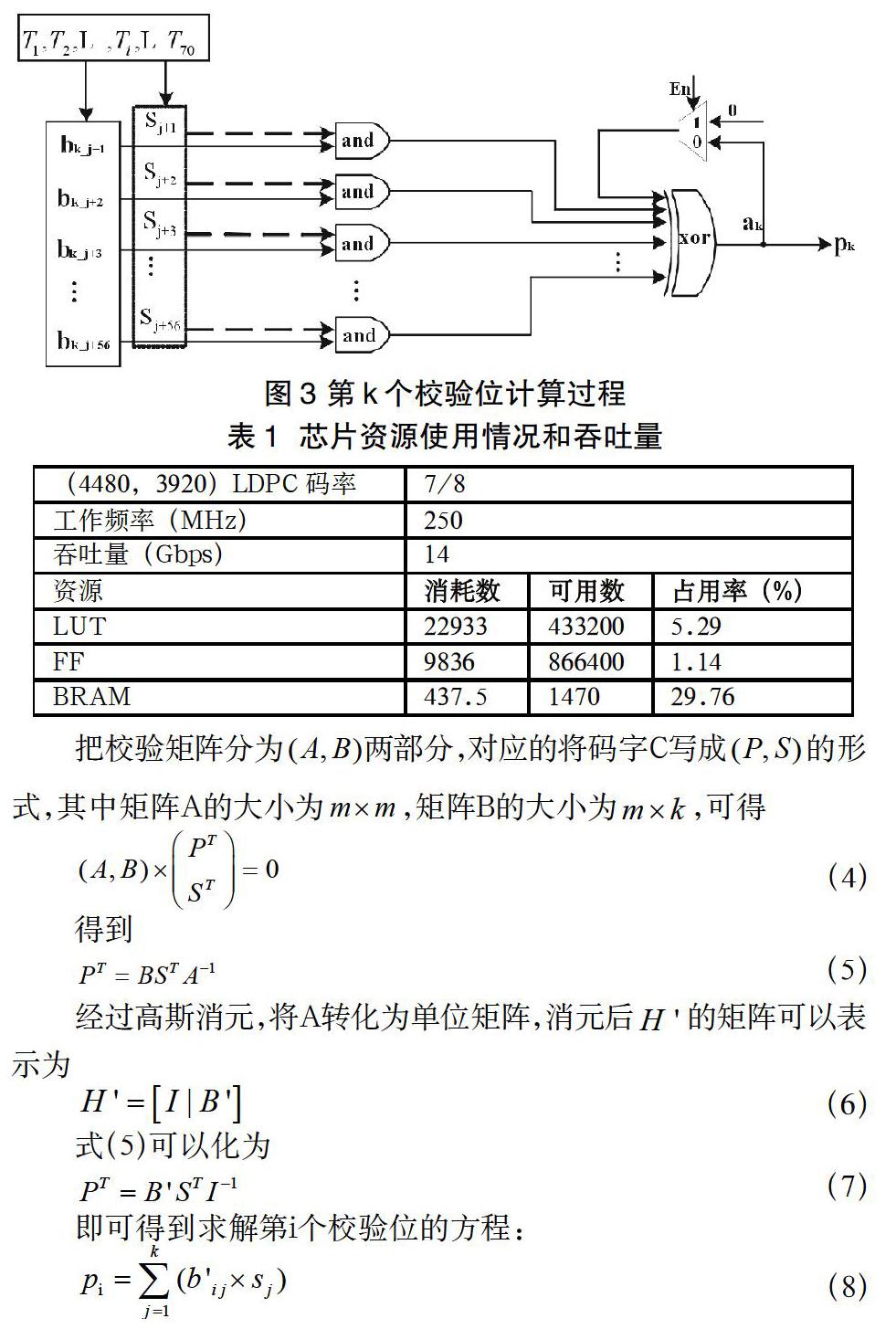
每个校验位的计算只与矩阵中的对应行相关,因此,本文提出了一种校验位并行分步计算方案,即每个时钟周期,56个信息位分别在560个逻辑运算电路内,与对应的子矩阵中560行、56列元素进行运算,经过70个时钟周期,即可同时计算出560个校验位。
以第k个校验位的计算为例(如图3):第1个时钟周期,矩阵的第k行1到56个元素与并行输入的56个信息位一一对应,分别进行逻辑与运算,得出的56个变量与ak(初始值为0)执行异或运算,得出的结果更新到ak,并作为反馈信号参与到下一周期运算;第2个时钟周期,更新后的56路信息位,与矩阵的第k行中57到112个元素执行相同运算,而后与上一周期得出的ak进行异或运算;依次类推,直到第70个周期运算结束,得出结果即为对应的校验位pk。
图3中,Ti表示第1到第70个时钟周期数,b表示矩阵第k行的元素,S表示信息位,设,则。
3.2 校验矩阵的分层存储
由于一帧数据运算需要70个时钟周期,在存储时,对矩阵进行如下处理(图4):
(1)将矩阵按每80行为1层,共分为7层,每层含个元素;定义7个ROM块,分别把矩阵的第1层至第7层存储到ROM1到ROM7中。
(2)矩阵的每层,按每56列分成70个矩阵块,每个矩阵块大小为,含4480个元素;对应的,定义每个ROM块深度为70,宽度为4480比特。7个ROM块的每一存储单元,对应存储一个大小的。
(3)每个矩阵块中的元素在对应的存储单元中是按行分布的。以ROM1为例,设矩阵第1层的元素可以用表示(),则对应的存储单元对的存储顺序如图5所示。
这样,7个ROM块的每个地址,各自对应矩阵中的80行、56列元素。在第k个计算周期上升沿,就可以同时对7个ROM块的第k个存储单元进行寻址,将矩阵中第k个56列数据一次性全部读出,输送到逻辑运算电路。
3.3 输入输出缓存设计
校验位需要70个时钟周期才能计算完成,需要对并行输入的56路信息位进行缓存,待校验位计算完成后,两者组成完整的编码码字,方可输出。
为此,本文设计了一个输入缓存模块,主要由56个串/并转换模块组成,每个串/并转换模块对应一路输入信号,将一帧56路并行、每路串行输入70个信息位的信息序列,经70个时钟周期,转换成3920路并行输出。此时,560个校验位计算完成,与3920路并行输出的信息位组合成完整的编码码字,传递到输出缓存模块。
输出缓存模块与输入缓存原理相似,而功能相逆。组合后的4480路并行输入的码字传递到输出缓存模块后,被转换成64路并行信号,每路串行输出70比特数据。
3.4 控制模块设计
控制模块是编码器的核心模块,作用是:信息序列输入的同时,输入一个使能信号Rx_en,使存储模块地址Addr和控制模块中的计数器初始化为零,对7个ROM块进行寻址,逻辑运算模块开始工作。随后,每经过一个时钟周期,地址Addr和计数器自动加1。当第70个时钟周期结束,一帧数据运算完成,计数器达到预定值,产生一个使能信号Data_en,启动输出缓存模块输出编码码字。
4 实现结果及分析
本设计采用Xilinx公司的Vivado 14.4版本的硬件开发软件,以Virtex-7 系列芯片为硬件平台,进行了综合和布局布线后,编码器FPGA资源消耗情况和吞吐量如表1所示。
本文所设计的编码器LUT资源使用仅占芯片的5.29%,BRAM存储资源使用也仅占芯片的29.76%,布局布线后的工作时钟频率可以达到250MHz,吞吐量可达14Gbps。
5 结语
本文在对现有编码方案进行分析和对比的基础上,提出了一种基于优化的高斯消元算法的编码方案,该算法通用性强,适用于一般的LDPC码,并且在求校验位时便于实现行间高度并行的运算。在硬件实现上,设计了并行分步运算的快速编码结构,优化了矩阵的存储方法,简化了布线路径,降低了关键路径时延,达到了高速编码的目的。在基于Xilinx公司XC7vx690t FPGA芯片硬件平台上,本文设计的编码器工作时钟可以达到250MHz,吞吐量达到了14Gbps,且消耗资源较少,具有较大的工程应用价值。
参考文献
[1]Gallager R G.Low-Density Party Check Codes[D].Canbridge,MA:MIT Press,1963.
[2]肖扬.Turbo与LDPC编解码与应用[M].北京:人民邮电出版社,2010.
[3]R.M.Neal.Sparse matrix methods and probabilistic inference algorithm.IMA Program On Codes,Systems,and Graphic Models,1999.
[4]Richardson T, Urbanke R. Efficient encoding of low-density parity check codes[J]. IEEE Transactions on Information Theory,2001,47(2):638~656.
[5]M.P.C. Fossorier. Quasi-Cyclic LDPC low-density parity-check codes from circulant permutation matrices[J].IEEE Trans.Inf.Theory,vol.50,pp.1788-1793,Aug.2004.
