基于马尔柯夫预测模型的智能停车有效泊位预测研究

韩二锋

摘要：随着绍兴城市化水平的不断提升与城镇居民私家车拥有量的迅速增加，有限的停车位无法有效解决停车的问题显得越来越突出。通过调研，确定以绍兴市世茂广场停车场作为研究对象，基于马尔柯夫预测模型进行短时有效泊位的验证分析。通过计算，运用马尔柯夫预测模型所得的预测结果可信度较高，可在智能停车诱导系统模块中加以使用。

Abstract： With the increase of the level of urbanization in Shaoxing and the rapid increase in the amount of private cars in urban residents， the problem of limited parking spaces can not effectively solve the parking problem is becoming more and more prominent. Through the investigation， to determine the Shaoxing Shimao Plaza parking lot as the research object， analysis Markov forecast model based on short-time effective berth. By calculation， the reliability of the forecast results obtained by using the Markov forecast model can be used in the intelligent parking guidance system.

关键词：灰色模型；马尔柯夫预测模型；时间序列；世茂广场；有效泊位；可信度

Key words： grey model；Markov forecast model；time series；Shimao Plaza；effective berth；reliability

中图分类号：U491.1 文献标识码：A 文章编号：1006-4311（2016）06-0215-04

0 引言

绍兴统计年鉴（2014版）数据显示，截止2013年底，民用车辆拥有量111万辆，比上年末增长10.4%。其中汽车74万辆，增长17.8%。随着绍兴城市化水平的不断提升与城镇居民私家车拥有量的迅速增加，有限的停车位无法有效解决停车的问题显得越来越突出。作为动态交通的起点和延续，停车设施与服务供给不足以及管理滞后等静态交通问题也日益凸显，引起居民对城市交通的负面反馈。

停车场的有效泊位具有不确定性、随机性、相似性、周期性和波动性的特征。本文通过马尔柯夫预测模型对智能停车有效泊位进行仿真研究，经建模和数据预处理，计算所得预测数据与调查真实数据相比具有较高可信度。基于马尔柯夫预测模型的智能停车诱导系统有效泊位研究可以作为有效泊位的预测方法，并在智能停车诱导系统模块中加以应用。

1 马尔柯夫预测法

马尔柯夫预测法根据状态之间的转移概率来预测动态数据系统的发展规律，适合于随机性波动度较大的预测问题，但要求预测对象除具有马尔柯夫链特性外，还要满足平稳过程等均值特点。在实际过程当中，车位信息呈现非平稳随机性，时序数据会呈现波动和跳跃。

1.1 马尔柯夫预测基本原则

在预测过程中，首先遵循实事求是原则，认真整理并核实各项调研资料。其次遵循系统性和概率性的原则，找出其本质联系。确定适当模型后再根据连续性原则，将预测对象过去和现在的规律延伸到未来[1]。

1.2 马尔柯夫预测预测步骤

灰色理论能够建立微分方程预测模型基于以下几方面[2]：

①灰色理论将随机变量当作是在一定范围内变化的灰色量，将随机过程当作是在一定范围，一定时段内变化的灰色过程；

②灰色系统将无规律的历史数据列累加后，对生成数列建立微分方程模型；

③灰色理论通过GM模型来调整、修理、提高精度；

④对于高阶系统建模，灰色理论是通过GM（1，n）模型建解决的；

⑤GM模型所得数据必须经过逆生成，即累减生成作还原后才能应用。

马尔柯夫预测模型的预测步骤可用图1表示。

2 预测模型的建立

2.1 灰色模型（GM）的建模原理

灰色模型（GM）的建模原理见图2。

3 调研数据及预测验证

2014年1月9日至2014年1月15日，绍兴汽车服务业公共科技服务平台项目小组开展了绍兴市停车场调研活动。通过比较分析，确定以世茂广场停车场作为研究对象开展智能停车诱导系统研究：

①世茂广场业态丰富，消费具有代表性：世茂广场拥有百盛百货、欧尚超市、世茂国际影城等13家主力商家和500多个国内外知名时尚品牌。

②迪荡新城已有智能停车诱导系统相关设施，便于推广应用：世茂广场所处迪荡新城核心区域共设置12块电子显示屏，从上面可了解迪荡地下车位信息。

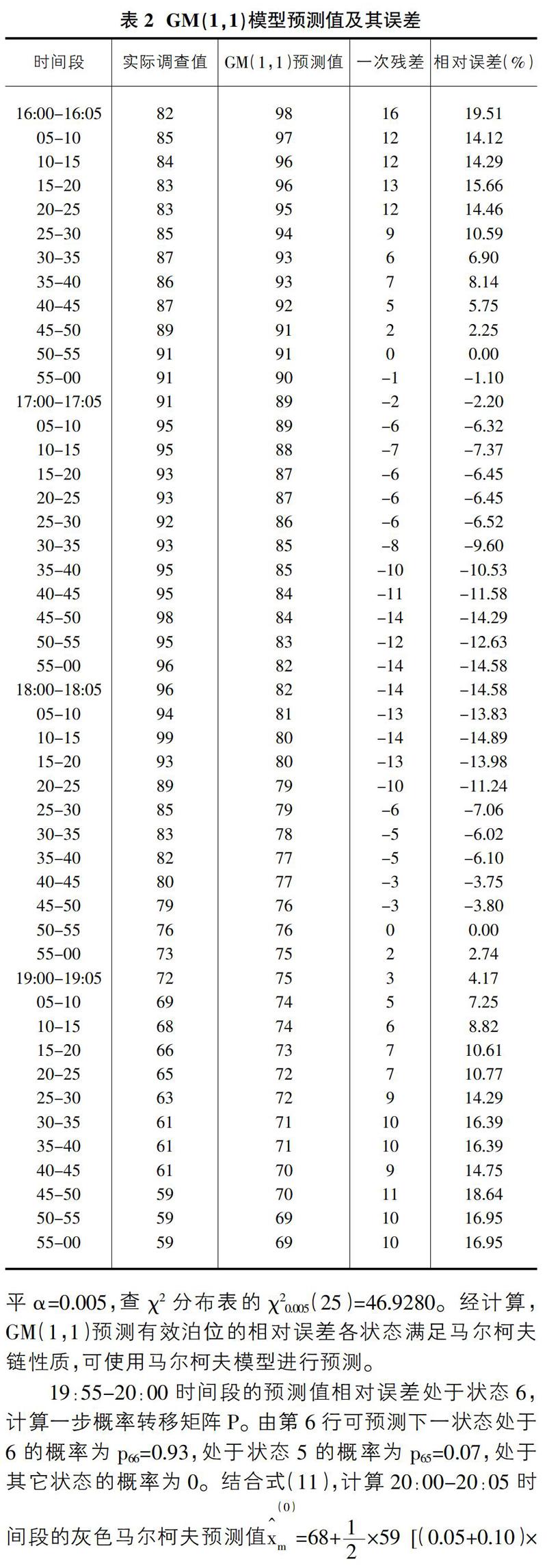
为了检验模型的预测精度和验证方法的有效性，平台项目小组统计了绍兴市世茂广场停车场2014年1月12日16：00-21：00典型时间段内的有效泊位数。以5min为间隔，具体数据见表1。

从以上数据得出：仅由GM（1，1）结果平均相对误差为10.11%，在此基础上对相对误差用马尔柯夫模型加以修正，预测值的相对误差下降至4.62%。基于马尔柯夫预测模型的智能停车有效泊位研究具有较高的可信度，可在智能停车有效泊位预测模块中加以使用。

4 结语

停车场的有效泊位受许多因素的影响，存在极大的不确定性、随机性、相似性、周期性和波动性。本文以绍兴市世茂广场停车场为例，进行了基于马尔柯夫预测模型的智能停车有效泊位仿真研究，通过与调查所得到的数据进行对比，验证了马尔柯夫预测模型的精确度。随着新理论及新技术的应用，城市智能停车诱导系统对城市交通诱导的作用将进一步体现。充分发挥静态交通系统对改善城市交通所起到的积极作用，助力绍兴智慧城市建设。

参考文献：

[1]许增昭.基于泊位诱导及适时预测的智能停车管理系统研究[D].广州：华南理工大学，2010.

[2]邓聚龙.灰色预测与决策[M].北京：清华大学出版社.1986：125-134.

[3]宋光平.铁路货运量预测方法综述[D].北京：北京交通大学，2007.

[4]蔡岩.基于灰色预测模型的短期交通流预测研究[D].成都：西南交通大学，2009.

[5]何勇，鲍一丹，吴江明.随机型时间序列预测方法的研究[J].系统工程理论与实践，1997（1）：36-43.

[6]盖春英，裴玉龙.公路货运量灰色模型-马尔柯夫链预测方法研究[J].中国公路学报，2003，16（3）：113-116.

[7]胡群芳，徐伟，刘文.灰色马尔柯夫模型在交通量预测中的应用[J].河南科学，2005，23（2）：247-250.

[8]胡光宇.战略：预测与决策[M].北京：清华大学出版社，2005：169-184.

[9]罗积玉，妍媖.经济统计分析方法及预测[M].北京：清华大学出版社，1987：347-348.

[10]夏乐天.马尔柯夫链预测方法及其在水文预测中的应用[D].南京：河海大学，2005.