Excel和Origin在密立根油滴实验中的应用
2016-05-14杨欣
杨欣


0引言
密立根油滴实验是近代物理学发展史上一个十分重要的实验。通过对带电油滴电荷量的测量,证明了电荷的“量子性”并精确测定了基本电荷数值[1]。该实验原理设计巧妙、仪器设备简单、结果计算准确,是一个非常具有启发性的实验。然而,在油滴实验数据处理方面,一般会采用“倒着推”的方法,需多次测量油滴的下落时间t和平衡电压U,造成实验运算量大、计算结果易产生错误等问题,故油滴实验数据处理也是物理实验教学研究的热点之一[24]。编程或软件设计等方法对计算机水平要求较高,不易掌握,故本文利用Excel 和Origin两个较为常用的计算机软件,对测量数据进行分析计算,并结合Origin强大的作图功能对合适油滴选择及粘滞系数η修正进行相关分析。这两种方法简单易学,对于深入理解实验原理,培养物理兴趣,处理数据及学科结合具有重要意义。
1密立根油滴实验原理
密立根油滴测电子电荷电量关键在于油滴电荷量q的测量[5]。一般采用两种方法,动态(非平衡)法及静态(平衡) 法。本文主要针对实验室常用的静态法进行分析。
当质量为m、电荷量为q的带电油滴静止于两平行极板之间时,油滴受到的重力与电场力达到平衡,即满足:mg=qUd(1)式(1)中,U代表极板电压,d代表两极板间距离,故只要测出油滴质量m即可得到油滴电荷量q。当对同一颗油滴不加电压时,油滴由于受到空气阻力Fr和重力mg的作用,将达到二次平衡,以速度vg匀速下落,这时根据斯托克斯定理,满足Fr=6πaηvg=mg(2)且油滴质量m=43πa3ρ,两式结合得a=9ηvg2ρg(3)其中,a代表油滴半径,ρ代表油滴密度,η为空气粘滞系数。由于油滴尺寸很小,需对粘滞系数η修正为η'。即η'=η1+bpa(4)整体带入最终得到 利用“倒着推”方法,油滴电荷量qi除以电子电荷公认值e0并取整,确定元电荷数ni [6]( ni为整数),即ni≈qe0(8)则实验所得的基本电荷e可以表达为这时,油滴半径a、质量m及油滴电荷量q为仅与油滴平衡电压U和下落时间t相关的量。同一颗油滴需多次测量平衡电压与下落时间,且为判断所选油滴是否为合适油滴,需测量多个油滴,这将产生大量重复计算工作,故通过Excel和Origin两种方法来简化问题。
2Excel在数据处理中的应用
电子表格Excel是一款常用的办公软件,具有很强的应用公式处理数据的能力。当在单元格内输入公式,利用粘贴功能即可实现相应单元格内数据的自动计算。针对油滴实验数据处理工作大量重复问题,可充分利用Excel的优势来解决问题。
2.1数据输入及公式编辑
根据式(10)、(11)、(12),利用Excel编辑公式如下:
2.2实验数据计算
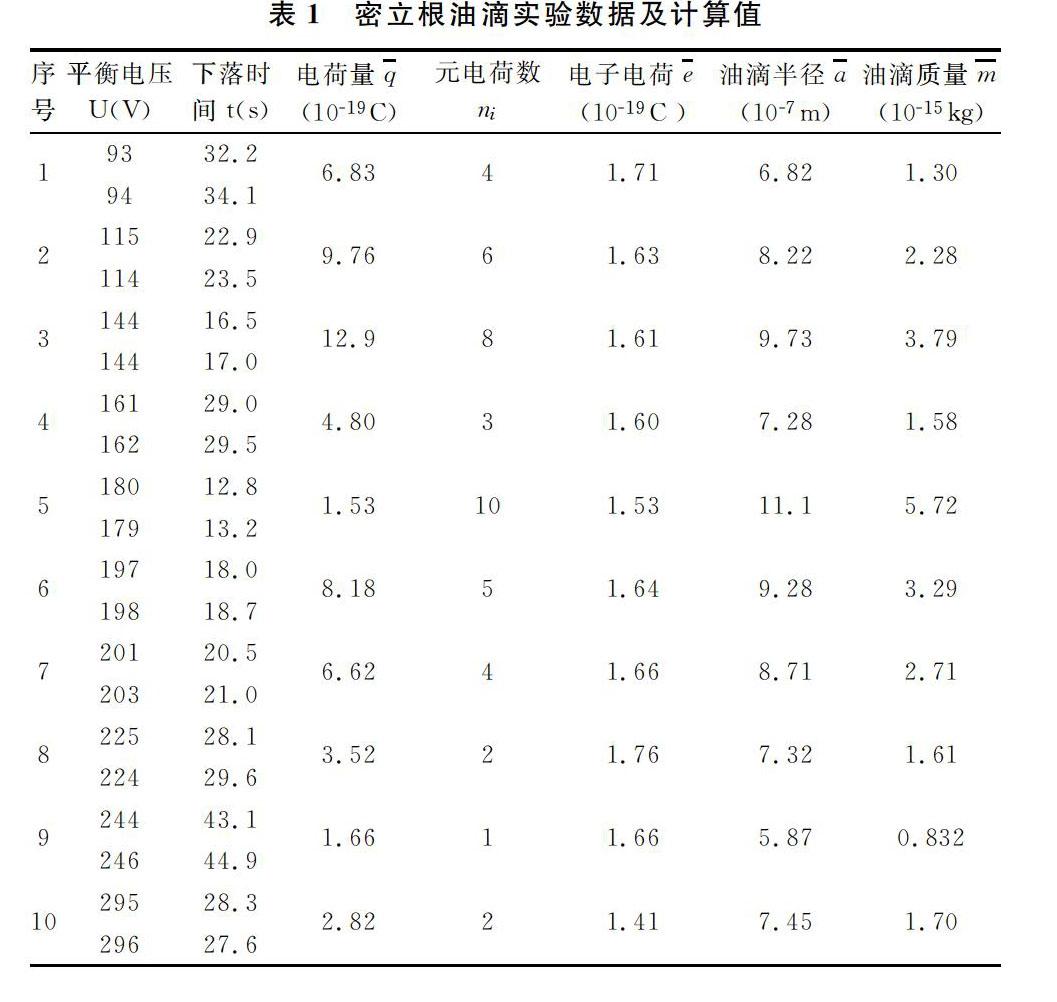
分别对10滴不同的油滴进行平衡电压和下落时间测量,且同一颗油滴测量10次。通过Excel进行相关计算,得到数据如表1所示。由于同一颗油滴测量时间和电压具有重复性和相近性,在表1中仅显示测量时间的两极。可以看出,计算结果清晰易懂,极大提高了计算的精度和效率。
除了拥有较强的数据分析能力外,还具有绘图功能,能直观筛选数据,并结合图像理解物理本质。
3.1Origin计算数据应用
启动Origin软件后,新建Worksheet,分别在U(X)及t(Y)输入油滴平衡电压及下落时间,通过add new columns 分别加入电荷量q(Y)、元电荷数ni(Y)、基本电荷e(Y)、油滴半径a(Y)以及油滴质量m(Y)。通过右键set column values分别输入对应的公式,即可得到相应的计算结果。例如电荷量q,公式编辑为col(q参照式(12)。对10滴油滴进行测量,将测量得到的平衡电压U和下落时间t带入,得到结果如表2所示。
可以看出Origin的计算功能与Excel一致,均可实现大量数据的简化处理。但Origin 除此之外,还具备强大的作图功能,可利用其分析合适油滴的选择及粘滞系数修正等实验重难点问题。
3.2Origin 在合适油滴选择上的应用
合适油滴的选择是本实验重点之一,将很大程度上影响实验原理的理解及实验结果误差的分析。判定所选择油滴是否满足实验要求,可通过Origin作图来分析。
可以看出,相同时间下,随着ni增大,电压值不断减小,具体变化规律利用Origin的作图功能拟合即可得到U-t曲线,如图1所示。可以看出,随着ni的增大,即电荷量q的增加,整个曲线越发紧密。当时间t较长时,对应平衡电压小,不同的ni会产生重叠,无法清晰判定元电荷数ni的大小,增大实验误差;当时间较短时,平衡电压大,整个曲线较为陡峭,无法较好地区分电压与时间的对应值,且对仪器要求较高。故合适的油滴指的是电压和时间处于曲线腹部,能较好地分辨出电荷的量子化,清晰区分ni的大小。合适油滴对应的测量值为:平衡电压200V左右,下落时间20s左右,元电荷数ni应处于2、3、4、5、6附近。
在粘滞系数修正上的应用
在油滴实验中,由于油滴尺寸与空气分子的间隙相当,斯托克斯定律不严格成立,故需对粘滞系数η修正。修正对实验结果有何影响是理解实验的难点之一。利用Origin计算及作图功能,分别讨论修正前后的油滴半径a及U-t关系的变化。
式(3)及式(5)分别代表未修正及修正后的油滴半径a,且公式中未知量仅与时间t相关,故选t作为自变量t(X),a1(Y)和a2(Y)列分别代表未修正及修正后的油滴半径a。利用公式编辑后得到相关数值,如表4所示,这里给出19.5s~20.5s所对应的值。
对所得数据进行拟合,得到修正前后a-t图,如图2所示。可以看出,修正后整体油滴半径数值偏小,且数值差会随着时间的增加而增加。修正后t=20s与未修正的t=21.8s,油滴半径a的数值相等。这充分说明,未对粘滞系数η修正,相当于测量时间存在几秒的系统误差,将很大程度上影响元电荷数ni的确定,增大实验误差。
4 结语
本文提出了Excel与Origin两种方法处理密立根油滴实验数据,并通过Origin数据分析及作图解释了合适油滴的选择及粘滞系数η修正等实验重难点问题。实验结果表明,Excel与Origin两种软件能够有效处理大量实验数据;利用Origin作图功能可知,合适油滴对应电压为200V左右,下落时间为20s左右,粘滞系数的修正与否,直接影响元电荷数及基本电子电荷电量,从而影响实验误差。两种处理方法准确、简洁、高效,具有很强的借鉴性和可移植性,能有效避免大量重复计算工作,减轻数据处理工作量;同时,数据处理方法的多元化,在学科结合、创新意识及兴趣培养上具有重要意义。
参考文献:
王小平,周庚宽,王丽军,等.大学物理实验.北京:机械工业出版社,2010.
周海涛,唐美玲.密立根油滴实验数据分析软件的设计[J].实验室科学,2009,6(3):7375.
陈晓,唐定飘.密立根油滴实验的探究性数据处理方案[J].大学物理实验,2013,26(4):8890.
曹彪,邹文辉,代伟.Matlab 在密立根油滴实验数据处理中的应用[J].西华师范大学学报:自然科学版,2015,36(9):317319.
邱成锋,杨嘉,张金凤.密里根油滴实验中两种方法分析平衡电压和下落时间选取[J].大学物理实验,2014,27(4):5658.
