基于MATLAB的互联网中最优负载潮流分析

栗明

摘要：负载潮流分析是电力系统规划设计与运作的基础。运用不同方法如牛顿-拉夫逊迭代法、高斯-赛德尔和快速解耦方法，成功地解决了负载潮流测试案例中的互联配电系统问题。对IEEE-30母线网络测试结果表明，牛顿-拉夫逊法能够获得负载潮流问题的最佳解决方案。通过MATLAB编程，得到了降低功率损耗的解决方案和补救措施的实现方法。

关键词关键词：负载潮流；牛顿-拉夫逊迭代法；高斯-赛德尔迭代法；快速解耦方法；MATLAB；互联系统

DOIDOI：10.11907/rjdk.161310

中图分类号：TP301文献标识码：A文章编号文章编号：16727800（2016）007003603

0引言

在各种形式的能源中，电能在发展中国家起着非常重要的作用。为了获取电力，需要建立一个庞大的互联网络。电力系统网络是世界上最大的人造系统。为了获得系统参数值，需要对该系统网络进行深入研究。当电力系统运行时，经常从一个状态切换到另一个状态。因此，系统可能处于稳定或暂态状态。在这两种情况下，需要分别对系统条件进行分析，以更好地进行操作和控制。

本研究可以分为3个阶段：网络建模、数学建模和解决方案。在网络建模阶段，设备被表示为一个等效电路元件；在数学建模阶段，借助于适用的规律，可将网络模型转化为数学模型。该模型方程求解可通过MATLAB编程获得。根据研究中开发的代数方程类型，选取对应的数值方法来解决。数学表达式的解给出了参数值，有助于判断系统是否稳定或可控。而相比于具备安全性和可靠性约束的隔离系统，互联系统提供了更好的负载和操作处理方案。1负载潮流分析

负载潮流计算是电力系统分析中最常用的计算过程之一。负载潮流研究决定了系统电压、电流、有功和无功功率、功率因数和功率损耗。负载潮流研究是进行系统规划一个很好的工具，可以用于分析操作阶段，如发电机、输电线路、变压器或负载等的损耗，也可用来决定电容器的大小和位置来提高功率因数。以下3种方法主要用于解决负载潮流问题：①牛顿-拉夫逊迭代法；②快速解耦潮流法；③高斯-赛德尔迭代法。

2负载潮流方程

为了推导进入母线的有功和无功功率方程，需要定义以下变量。令第i根母线的电压为：

上式即为负载潮流方程。

第i根母线注入的总有用功率即可表示如下：

令通过负载潮流程序计算出的注入功率为Pi，calc，不匹配量为：

类似地，无功功率与计算值之间的不匹配量可以表示为：

负载潮流的目的是为了最小化以上提到的两个不匹配量，式（6）、（7）用于计算式（9）、（10）中的有功功率和无功功率。

3技术方案

由于上述功率流方程的非线性和解析表达式的复杂性，采用如下数值迭代技术： 3.1高斯-赛德尔迭代法

高斯-赛德尔方法是另一种通过逐次估计节点电压解决负载潮流问题的迭代技术，算法步骤如下[4-6]：①在每根母线负载分布已知的情况下，如PD、QD已知，将Pca和Qca分配给所有发电站；②用节点导纳矩阵Ybus装配母线，将并联导纳数据存储在计算机中，Ybus是利用自互导纳的规则组装的；③母线电压迭代计算（Vij=2，3…，n）： 假设启动一组初始电压值的迭代；④松弛节点功率计算：用趋于S*=P-jQ的Vi替换步骤3中所有的母线电压；⑤线流量和线路损耗计算：是负载潮流分析的最后一步，计算网络中每种线路的功率流，设母线i和j相连。

3.2牛顿-拉夫逊迭代法

高斯-赛德尔迭代法（G-S）相对较为简单，但牛顿-拉夫逊迭代法（NR）有更好的收敛特性且速度更快。牛顿-拉夫逊迭代法步骤如下[4-6，8]：

步骤1：选取除松弛节点外所有节点电压模值的初始值。

步骤2：用被估值V（k）和δ（k）计算所有的有功功率P（k）calc以及相等数量的有功功率不匹配量ΔP（k）。

步骤3：用被估值V（k）和δ（k）计算所有的无功功率Q（k）calc以及相等数量的有功功率不匹配量ΔQ（k）。

步骤4：用被估值V（k）和δ（k）表示雅克比矩阵J（k）。

步骤5：用JΔδ2

步骤6：更新公式如下：

步骤7：如果所有的不匹配量较少，则需要检查。判断该过程是否结束，否则返回步骤1开始下一个循环更新。

3.3快速解耦潮流法

功率流程序设计步骤如下[7]：

步骤1：输入原始数据。在标准数据结构中输入电网数据并估计剩下的未定义母线模值与相角起始点。

步骤2：数据恢复。指定数据线和母线数据同时随着母线序号变化而变化。

步骤3：估计母线导纳矩阵Ybus。

步骤4：估计功率不匹配值。从实际的功率不匹配式（9）和（10）分别估计ΔPi和ΔQi。

步骤5：估计雅可比矩阵中各个元的值。

步骤6：估计增量。用高斯-赛德尔消元法估计功率潮流矩阵中母线电压模值的增量ΔV和母线相角增量Δδ。

步骤7：更新变量。使用如下公式来更新母线电压模值和相角。然后返回步骤5，用新值替换旧值：

步骤8：检查每个PV节点的无功功率。

步骤9：终止条件。过程一直进行到残差ΔP（k）和ΔQ（k）小于如下的公差精度：

记ζ为一个很小的正数，如0.001、0.000 01，并且值越小，精度越高。

步骤10：估计每个PV节点的无功功率以及每个平衡节点的有功功率和无功功率。

步骤11：对母线重新编号。从每根母线编号返回至母线数据矩阵和线路数据矩阵中的原始母线编号。

步骤12：估计线流和损耗。估计输电线路和变压器的实际和无功功率流，以及设备损耗。

4最优功率潮流问题解决方案

4.1潮流问题（IEEE-30母线系统）

案例研究主要用于评价各种分析方法并实现高斯-赛德尔、牛顿-拉夫逊和快速解耦潮流方法的计算机程序，利用其给出IEEE-30母线测试系统最优潮流技术的解决方案。

4.2测试结果

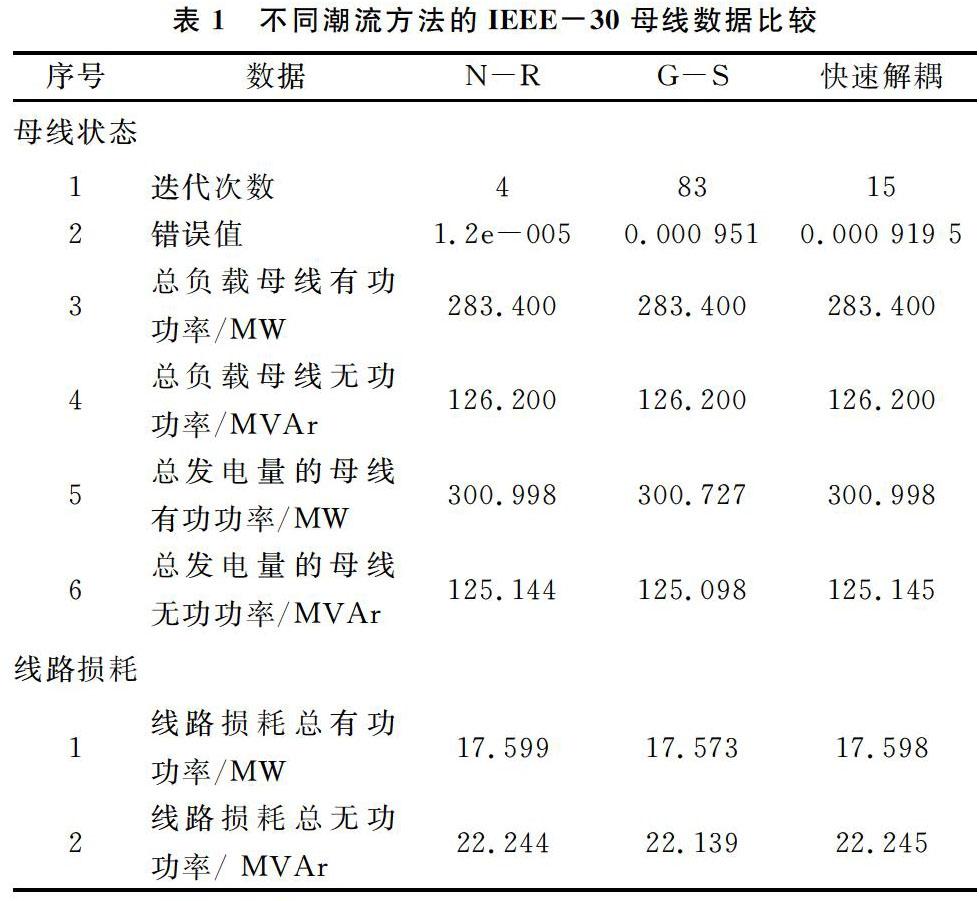
负载潮流分析在IEEE-30母线测试系统中执行，输出牛顿-拉夫逊、高斯-赛德尔以及快速解耦潮流的电压模值和电压相角、负载母线有功和无功功率、发电站母线有功和无功功率与线路损耗值。

高斯-赛德尔方法的收敛速度慢于其它两种方法。相比于网络中没有母线，高斯-赛德尔方法没有迭代增加的趋势，然而牛顿-拉夫逊迭代法和潮流计算的快速分解法中迭代速度很慢。

高斯-赛德尔方法最主要的优点是程序设计非常容易，能够最有效地使用主内存；潮流快速分解法中对于存储的要求大约是牛顿-拉夫逊迭代法的60%，但比高斯-赛德尔方法略多；牛顿-拉夫逊迭代法的缺点是编程较为复杂并且需要很大的电脑内存。但由于其精度高、迭代次数少，牛顿-拉夫逊迭代法适合潮流和稳定性研究，并可用于扩展变压器抽头变换操作、约束母线电压变量，以及确定最佳的有功和无功功率调度。高斯-赛德尔方法只对较小的母线系统有效，其可靠性低于潮流计算的快速分解法。当然对于任何系统而言，牛顿-拉夫逊迭代法都是最可靠的。5控制技术

5.1负载分配

如表1所示，母线编号为5的有效负载是94.2 MW，并且线路损耗为17.599MW/22.244MVAr。修正步骤为：对于高负载的5号母线，在修正的5号与7号母线的负载分别为84.8MW和32.2MW的条件下，7号母线分配给其10%的负载。如表2所示的仿真结果，即是通过把线路损耗降低到17.536MW/21.976MVAr的范围内而获得的。

相比于其它母线电压，30号母线电压较小，说明输电线无功功率流容量不能满足无功负载的需求。这种情况可以通过在30号负载母线上安装无功发生器来补救。注入正的无功功率后，通过向系统注入10%MVAr的功率来降低线路损耗。如表1给出的数据显示，PU节点电压模值小于额定电压0.995，线路损耗达到17.599MW/22.244MNAr。修正步骤为：定义30号母线为薄弱母线，向30号母线注入额外的无功功率1.0MVAr。如表3所示的仿真结果，即是通过把线路损耗降低到17.578MW/22.1415MVAr范围内而获得的。

如表1所示的数据，变压器的抽头位置反馈至4号母线的值为0.932。线路损耗达到17.599MW/22.244MVAr。修正步骤为：把变压器的抽头位置放置在1而不是0.932处。如表4所示的结果，即是通过把线路损