初中数学中空间与图形的教学探析
2016-05-14王海英
王海英
摘 要:空间与图形是中学数学教学中的重要内容,掌握空间与图形之间的转化思维,是中学数学中重要的解题思路。它能有效地锻炼中学生的空间想象力,帮助中学生更好地解决几何问题。主要讨论中学数学中空间与图形的相互转换策略,以帮助中学生更好地解决中学几何问题。
关键词:数学教学;空间;图形
《义务教育数学课程标准》中要求,中学生需要熟练进行空间与图形之间的相互转换,并根据实物的形状想象出相应的几何图形,对较为复杂的立体模型能从中分辨出几何图形的基本元素与联系。空间与图形的教学主要分为从表象认知→抽象概括→结合实际→掌握运用,教师应始终遵循这个原则,引导中学生掌握空间与图形转换之间的要点。
一、帮助中学生熟练掌握各空间与图形的特点
初中数学中,基本的图形主要为矩形、正方形、梯形、三角形和圆形。每一个图形都有其自身固有的特点,如矩形又称为长方形,矩形内共有四个角且都是直角,同时矩形的两组对边分别相等,而且在平面内任一点到其两对角线端点的距离的平方和相等。而正方形是特殊的矩形,因为其不仅满足矩形所有的特点,且四边均是等长。
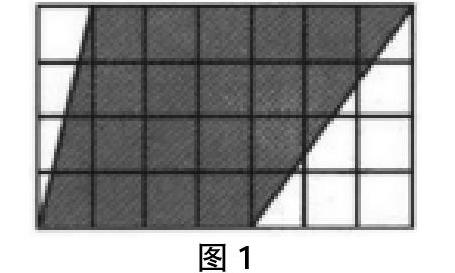
初中数学中常见的空间有长方体、正方体和圆柱体。长方体是由两个正方形和四个长方形组成的;正方体是由六个正方形组成;圆柱体是由两个圆和一个长方形组成。中学生只有熟练掌握了各个空间与图形的特点,才能够很好地识别并进行转换。如图1,可以看出有几种图形。
根据图形自身的特点,我们可以看出,图1中有三角形、矩形和梯形。
除了采用直观的图像方式让中学生了解空间和图形的特点,教师还可以让中学生亲自动手操作。如,可以准备一个长方体的纸盒(如鞋盒),让中学生自己测量长方体的边,自己辨认长方体每一面的图形,以此加深中学生对空间和图形特点的感知。
二、提升中学生空间想象力,掌握空间与图形之间的联系
空间是由多个图形组成的,如长方体是由矩形组成,圆柱体是由圆和矩形组成。只有了解这些空间基本的组成元素,中学生才能合理地发挥空间想象力,并将之与相关的图形进行联系,从而找到解题的方法与思路。
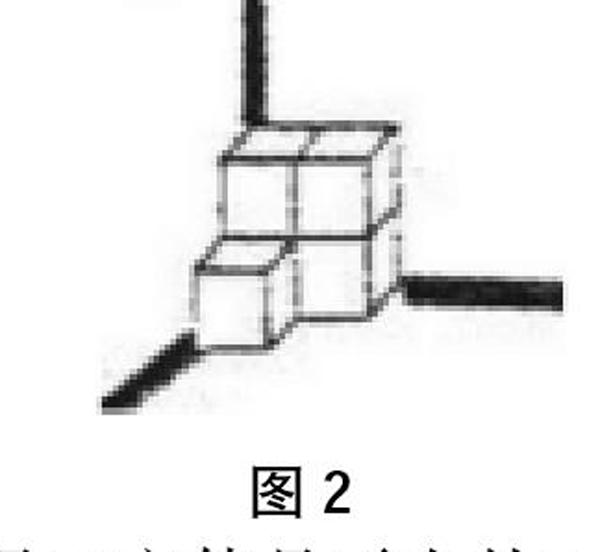
如图2,5个棱长为30厘米的正方体放在墙角,求露在外面的表面积是多少平方厘米。
分析:题目所求是正方体是露在外面的表面积,而正方体的表面积是由6个正方形组成。若要求露出的表面积,只需了解露在表面的正方形有几个,并求出总面积即可。从图2中可以看出,露出的正方形有10个,所以只要算出这10个正方形的总面积
即可。
解:30×30×10=9000(平方厘米)
所以,露在外面的表面积为9000平方厘米。
三、利用空间与图形帮助中学生解决实际问题
任何知识的学习最终都是为了能更好地解决生活中的问题,数学知识也不例外。空间与图形的问题在现实生活中比比皆是,教师要重视将空间与图形的知识点与中学生的实际生活联系在一起,如此才能更好地激发中学生对数学的学习兴趣,帮助中学生更好地进行空间与图形的转化。生活中中学生遇到的空间与图形的问题主要可以分为两类,一类是图形之间的转化问题,一类是空间与图形之间的问题。根据所遇到的问题采用相应的转化思维,就能很快找到解题的要点与思路。
1.图形之间的转换在实际生活中的运用
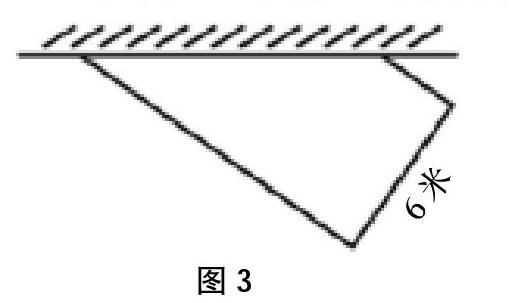
已知,王大伯就着一堵墙,将篱笆围成了一个梯形且其中一边长为6米,见图3。已知篱笆总长为20米,求篱笆所围的面积。
分析:从图3可以看出篱笆所围成的图形是一个直角梯形。根据梯形的面积公式=(上底+下底)×高÷2,和已知条件篱笆总长为20米,梯形的高为6米,所以(上底+下底)=20-6=14米。所以梯形的面积公式=14×6÷2=42(平方米)。
2.空间与图形在实际生活的运用
如图4,左边的图形是右边的第几个正方体的展开图?
分析:从左边图形可以看出,黑点与白点对应,并位于正方体的底部和顶部,所以可以A项选择便可排除。图形中两个三角形是角对角的连接在一起,所以可以排除C选项,故而选B选项。
现代认知心理学发现,表象认知是中学生学习与操作空间与图形的基础,是进行空间与图形相互转化的重点。所以,教师要重视中学生对图形表象的建立,提供大量有关空间与图形的材料,加深中学生对空间和图形的认识与联系。在教学过程中,教师要重视培养中学生的空间想象能力与逻辑思维能力,加深中学生对空间和图形之间联系的了解,并结合实际生活,帮助中学生逐步建立抽象空间与图形的概念,中学生才能逐步掌握空间和图形之间转化的要点。
参考文献:
[1]刘晓玲.数学空间与图形教学创意与策略探析[J].延边教育学院学报,2013(1):100-102.
[2]刘长福.在数学“空间与图形”教学中渗透转化思想[J].科学咨询:教育科研,2014(2):77-78.
[3]夏梅.数学教学策略研究:以空间与图形的教学为例[J].学周刊,2016(7):84.
编辑 薄跃华
