运用“矢量圆”解题几例

徐飞翔

摘 要：已知一个矢量的大小和方向及另一个矢量的大小，这类矢量的动态变化问题，常使学生感到困惑，不易解决。如能灵活运用矢量圆结合平行四边形定则或三角形定则，会使问题化繁为简，易于学生理解。这样，既能使学生开阔思路和开拓视野，又能使学生加深对矢量问题的理解，提高他们运用数学知识分析、解决物理问题的能力。

关键词：矢量；动态变化；矢量圆

中图分类号：G63 文献标识码：A 文章编号：1673-9132（2016）23-0207-02

DOI：10.16657/j.cnki.issn1673-9132.2016.23.132

矢量既有大小，又有方向，且运算时满足平行四边行法则。在一些问题中常会遇到矢量的动态变化问题。例如，已知一个矢量的大小，但是其方向不确定，我们姑且称之为矢量的动态变化，由动态变化问题衍生出求矢量合成与分解中的极大值、极小值及多解等问题。这类问题常使学生一筹莫展，不知如何下手。对于已知一个矢量的大小和方向及另一个矢量的大小，但方向可变的问题，若能借助圆的半径表示矢量的大小，以圆心向外的指向表示矢量的可能方向，建立一个“矢量圆”，用来表示物理学中的速度、力等矢量的变化，就能结合具体问题，使问题形象直观，有效地化繁为简，使学生易于接受，并能加深他们对矢量概念的理解。

一、“矢量圆”在运动的合成中的运用

小船渡河是典型的运动合成的问题，常作为重要模型考查学生对运动的合成的理解。求渡河最短时间及最短位移问题是常见题型，下面通过例题讨论如何运用“矢量圆”解决问题。

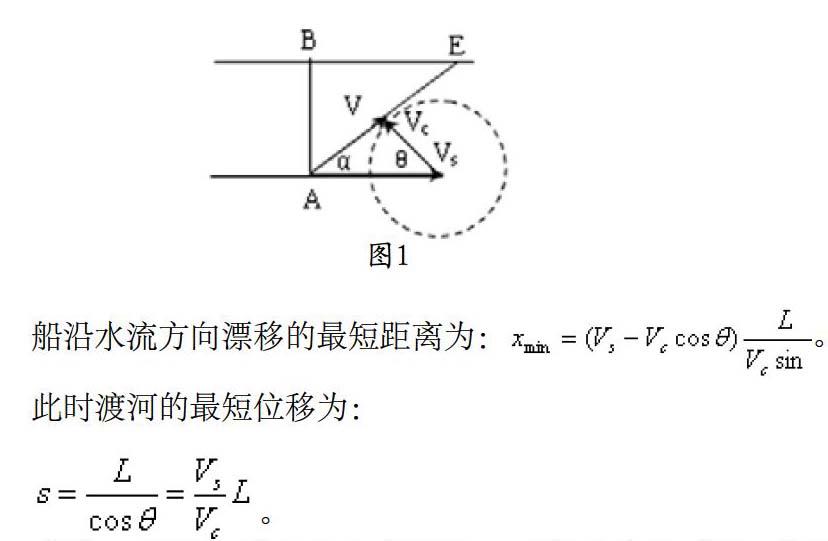
例1：一条宽度为L的河流，水流速度为Vs，已知船在静水中的速度为Vc，且Vc

分析：如果水流速度大于船在静水中的航行速度，则不论船的航向如何，总是被水冲向下游。怎样才能使漂下的距离最短呢？如图1所示，设船头Vc与河岸成θ角，合速度V与河岸成α角。可以看出：α角越大，船漂下的距离x越短，那么，在什么条件下α角最大呢？以Vs的矢尖为圆心，以Vc为半径画圆，当V与圆相切时，α角最大，根据cosθ=，船头与河岸的夹角应为：θ=arccos。

小结：本题中的水速大于船速，不能到达正对岸，但沿怎样的方向航行才能使船的向下漂移的位移及渡河的位移最短呢？因船头的方向有无数种可能，用平行四边形定则进行处理过于复杂，学生也不具备这样的数学能力，这里借助矢量圆使问题变得形象直观，简化运算的过程，学生易于接受。

二、“矢量圆”在力的分解中的运用

力是矢量，既有大小，又有方向。在已知一个力进行分解的时候，有无数种可能，如加上一定的约束条件，讨论力的分解问题，求符合条件的解的个数。这类问题常使学生感到棘手，若能运用矢量圆结合平行四边形定则进行处理，会使问题形象直观、大头简化。

例2：如图2所示，已知合力F大小方向，一个分力F1的大小和另一个分力F2的方向，讨论解的个数。

分析：因为已知合力F的大小和方向，F2方向一定，可以画出一条与F一定夹角α的直线表示F2的方向，因为F1的大小确定，方向有无数种可能，若能用矢量圆的半径表示F1的大小，半径从圆心向外的指向表示F1的可能方向，就以F的矢尖为圆心，以F1大小为半径，作矢量圆，如图2所示画圆，结合三角形定则知道，若有解必会构成封闭的三角形，从而得出有无解及解的个数。

（1）F1小于Fsinα，圆与F2无交点，所以无解。

（2）F1等于Fsinα，圆与F2相切，所以有一个解。

（3）Fsinα

（4）F1>F，圆与F2也只能交一点，所以有一个解。

例3：把一个已知力F分解，要求其一个分力F1跟F成30°角，而大小未知，另一个分力F2=，但方向未知，则F1的大小可能为（ ）

分析：Fsinα

三、“矢量圆”在力的合成中的运用

运用矢量圆结合力的三角形定则可以分析动态平衡问题中的夹角的最大值问题。当已知合力F与其中一个分力F1的大小时，若F>F1，则另一个分力F2与合力F的方向间夹角有一最大值。如图5所示，以F的矢端为圆心，以F1的大小为半径作圆，当另一个分力F2与圆相切时，F2与合力F的方向间夹角有一最大值θ，满足sinθ=。

例4：如图6所示，重为G的小球，用一细线悬挂在点o处，现用一大小恒定的外力F（F

解析：如图7所示以重力的矢端为圆心，表示外力F大小的线段长为半径做一圆，根据力的合成，当绳的拉力和圆相切时，细线拉力的偏角最大如图6所示，故最大的偏角为sinθ=。拉力的大小为FT=Gcosθ。

通过以上几例可以看出，矢量问题灵活多变，对于这类问题，若能在解题中巧妙运用矢量圆进行分析，会使问题形象直观，便于理解，学生易于接受，还能简化解题过程，提高学生灵活分析和解决问题的能力。

[责任编辑 赵景霞]