借错启发 完善学生对高中数学的认知
2016-05-14田兆杰
田兆杰
摘 要:受应试教育的影响,无形之中我们总是对出现的错误感动恐惧和紧张。一方面教师看到学生出错动辄呵斥,从而造成学生的有意回避。实际这样的教学方式很容易让知识漏洞百出。所以本文结合新课程改革理念,对怎样鼓励和启发学生正确对待错误,以及如何借助错误完善认知进行论述。
关键词:高中数学;借错启发;知识漏洞
中图分类号:G63 文献标识码:A 文章编号:1673-9132(2016)23-0102-02
DOI:10.16657/j.cnki.issn1673-9132.2016.23.063
众所周知,学习的过程其实就是互动、探索的过程,也是发现错误、弥补错误、完善认知的过程。所以,教学过程中我们本该正确认知错误,并及时启发学生摆正态度探索弥补错误。但是在具体操作中,我们会发现许多学生甚至教师不是想办法发现错误,通过学习和认知弥补漏洞,而是有意无意地回避错误,这种讳疾忌医的态度和见到学生错误就训斥的态度都是不可取的。新课程改革以来,我们逐渐认识到学习和实践的过程就是通过失败积累成功经验的过程,所以教学过程中我们不能畏失败如虎,要引导学生敢于认知错误,从错误中受到启发,从而找到解决此类问题对应的方案,如此方能及时弥补知识漏洞,完善知识体系。鉴于此,我们就结合多年的数学课堂实践,对怎样巧用错误资源来启发学生完善认知进行以下几个角度的分析。
一、细分概念细节,修正感性认知
高中数学再难也有其原理,所以教学过程中我们一定不能忽视对数学概念细节的分析和阐述。数学是逻辑性很强的学科,概念描述所用的每一个字词都有关键性的作用,如果我们忽视、曲解,就会差之毫厘失之千里,在遇到数学问题时就会出现概念模糊或错误解析。所以,笔者建议在高中数学学习中,要先能将数学概念分析透彻、掌握牢固。当然,课堂教学中,限于学习能力的不同,学生在认知概念时肯定会有误区,这就需要我们对容易出错的地方进行诱导,从根源上防微杜渐,修正认知。
比如许多学生遇到函数就发慌,经常考虑不周全,这就是对概念细节把握不完善。许多学生会理解成“变量y随变量x的变化而变换,那么y应该x的函数”,顺着这样的思路就会曲解用映射的思想来解决函数问题。对“对变量X在某一范围内的每一个确定值,变量y都有唯一的、确定的值与之对应”这些概念性的东西模棱两可,不知所措。遇到这种情况,我们可以通过比较典型、具体的实例来修正学生的感性认知:y=︱X︱-X,然后演示:当X取任意非负实数时,y都有唯一的确定的值0与之对应;而当X为负实数时,就变成y=-2X。通过具体的形象解释,学生就能及时更正认知上的偏差,有效完善了概念认知,为规避以后出更大的错误奠定基础。
二、归纳常见错误,规避“阴沟翻船”
当下高考数学题目越来越细化,越来越开放。包括函数、不等式等在遇到实际问题时,我们要根据不同的情况综合进行分类讨论,这样才能优选出最佳答案。教学实践中,我们常听同学抱怨:“哎呀,怎么这个细节我没注意到”,为了规避这种风险,笔者就利用阶段复习,引导学生总结和归纳该类题常见的错误,然后进行一一启发,帮学生打开思路,引导他们发散思维,解决实际问题。
这里就拿经常容易出现忽略分类讨论的二次函数来说。该部分知识点考查力度比较大,也与实际问题结合得比较紧密,需要结合定义域或值域来考虑。所以我们在学完一段知识后,就要总结学生容易出错的地方,然后通过实际问题来诱导学生暴露错误,之后再进行有针对性地引导。看下例:当a为实数时,函救f(x)=(a-2)x2+(a-5)x-1的图像与x轴仅有一个交点,求实数a的值。
看到该题许多学生直接上手根据二次函数的思路进行解决:当二次函数f(x)=(a-2)x2+(a-5)x-1(a为实数)与x轴只有一个交点时,就是函数的定点在x轴时,这时存在△=(a-5)2+4(a-2)=0。求得结果是a无解。
这个过程看似天衣无缝,实际这个结果并不是完整的答案。这就是没有注意到细节,被传统的二元思维束缚了。我们仔细阅读,可以发现该题并没有说必须是二次函数,所以我们还要考虑(a-2)=0的情况。这时候f(x)=-3x-1,符合与X轴有只有一个交点(-,0)的要求。这样两个角度综合分析我们才能寻找到最恰当的方案。
这里我们会发现,做数学题一定要考虑周全。为了达到此目的,我们就要在单元学习之后引导学生对单元内的知识细节进行一一筛查,总结归纳出容易出错的地方,这样学生才能步步为营,夯实基础知识,提升数学运用能力。
三、通过黑板演示,暴露典型问题
数学课上,总有一些问题是学生普遍存在认知误区的,这种情况下我们就可以设置出典型问题,选几位学生上台在黑板上进行现场解答演示。这样让整个解题过程都暴露在大家眼皮下,台下的学生也会及时跟进思考,看看做题者有哪些优点和不足。这样就能有效杜绝普遍性问题躲避的疑难角落,并能结合实际过程给大家剖析和讲解。比如在教学函数单调性时,笔者发现许多学生对基本概念掌握不牢固,针对这情况我分别抽选了中下层三个层次的同学上台板演:
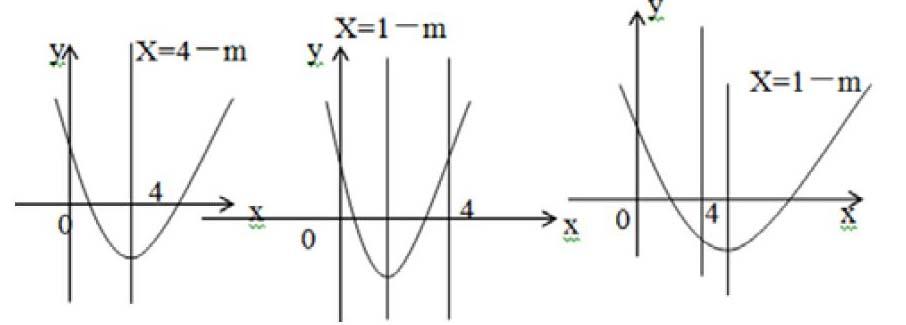
看下例:假如在定义域区间上是减函数,请画出示意图。这是一道最基础的题,让学生上台演示就是为深化大家的认知,杜绝出现不必要的理解歧途。我们看下面三位学生做的图,看看暴露出了什么问题:
首先我们要明白二次函数里对称轴是确定函数图形位置的关键,为了做准图,我们要先算出该二次函数的对称轴:X对=-=1-m,然后来一一分析这几个图:第一幅图画的对称轴是x=4-m,显然是忽略了函数在区间外也有一部分递减的可能,对称轴也考虑错了;第二幅图找对了对称轴,但是画出的函数在区间上有增有减,这就是没有掌握好函数单调性的意义;再看第三幅,对称轴是X对=1-m;函数在区间也是减函数,对了。
通过这样让学生将自己的思考过程展示出来,便于发现大家普遍存在的问题,然后再根据这些错误信息反馈就能及时给予启发和引导,帮助大家有效弥补知识漏洞,全面掌握数学概念和细节。
四、设置陷阱问题,启发学生深入反思
教学过程中也有一些问题如果教师不进行“干预”学生可能暂时遇不到。所以我们在备课过程中就要注意搜集学生容易出现理解错误的地方。只有这样让同学们来一次“阴沟翻船”,他们才能真正重视。
在学生为自己的“聪明”沾沾自喜时,我要求他们按常规解法进行解答,最终得到-3﹤x﹤2.5。两个结果不一致,学生蒙了。然后我们再启发他们认识到不等号两边同时约掉负数的话,不等号要换方向,所以(x+3)<0的情况没有分析到。看似如此简单的问题上出错的情况特别多,我们通过这样设置,将错出在练习阶段,就能有效弥补知识漏洞,养成全面考虑问题的良好习惯。
本文是我结合这几年的高中数学课堂实践对怎样巧借错误资源引导学生完善基础认知的分析与总结。俗话说:失败乃成功之母。学习过程就是师生互动讨论和分析问题的过程,我们只有在学习过程中不断发现错误、弥补错误,才能及时完善对数学的全面认知,才能在解决实际问题的过程中薄物细故,分析透彻,找到正确答案。
