AT、BT切石英晶体频率温度特性随切角变化关系研究

张鹏 陈丽丽

摘 要：从压电晶体的频率温度特性方程出发，计算了旋转Y切（yxl）石英晶体在参考温度T0=25 ℃时的一阶、二阶、三阶频率温度系数随切角的变化曲线，研究表明，一阶频率温度系数在θ取-49和35.2（o）具有零点值，分别对应AT和BT切的切割角度。AT切和BT切石英晶体频率温度曲线分别表现为三次函数和二次函数的曲线形式。AT和BT切石英晶体频率温度特性曲线随θ的变化以一定规律变化，θ的变化对AT、BT切石英晶体频率温度特性曲线的影响表现敏感。这些结论对AT、BT切石英晶体的设计具有重要的理论指导意义。

关键词：AT切 BT切 频率温度系数 频率温度特性

中图分类号：TN752 文献标识码：A 文章编号：1674-098X（2016）03（c）-0025-02

近年来，压电石英晶体振荡器由于在通讯领域中的大量应用而获得飞速发展。在压电石英晶体振荡器的设计中，石英晶体的切型是比较关键的一个环节，除此之外频率温度特性曲线也是需要着重考虑的。AT、BT切石英晶体都属于旋转Y切（yxl）族，其中AT切石英晶体是使用最多的一种切型，它的频率温度特性比较好，体积可以做得很小，可制作高Q值的超精密晶体，BT切石英晶体活力及频率温度特性较AT切差，但是其Z、T、C点比AT切易于控制，并且同样具有较高的Q值，因此也被广泛使用。AT、BT切石英晶体一般采用厚度场激励，对其频率温度特性影响的因素较多，其中角度的影响比较大，在设计过程中具有重要的地位。

1 理论计算

压电石英晶体的频率温度特性方程一般定义为[1-3]：

其中，为参考温度，一般取室温25℃，为温度为参考温度时的谐振频率，T为任意的温度，a0、b0、c0分别为温度为时的一阶、二阶和三阶频率温度系数，分别定义如下：

对以上各式综合考虑即可求得石英晶体的频率温度特性曲线。

2 结果和讨论

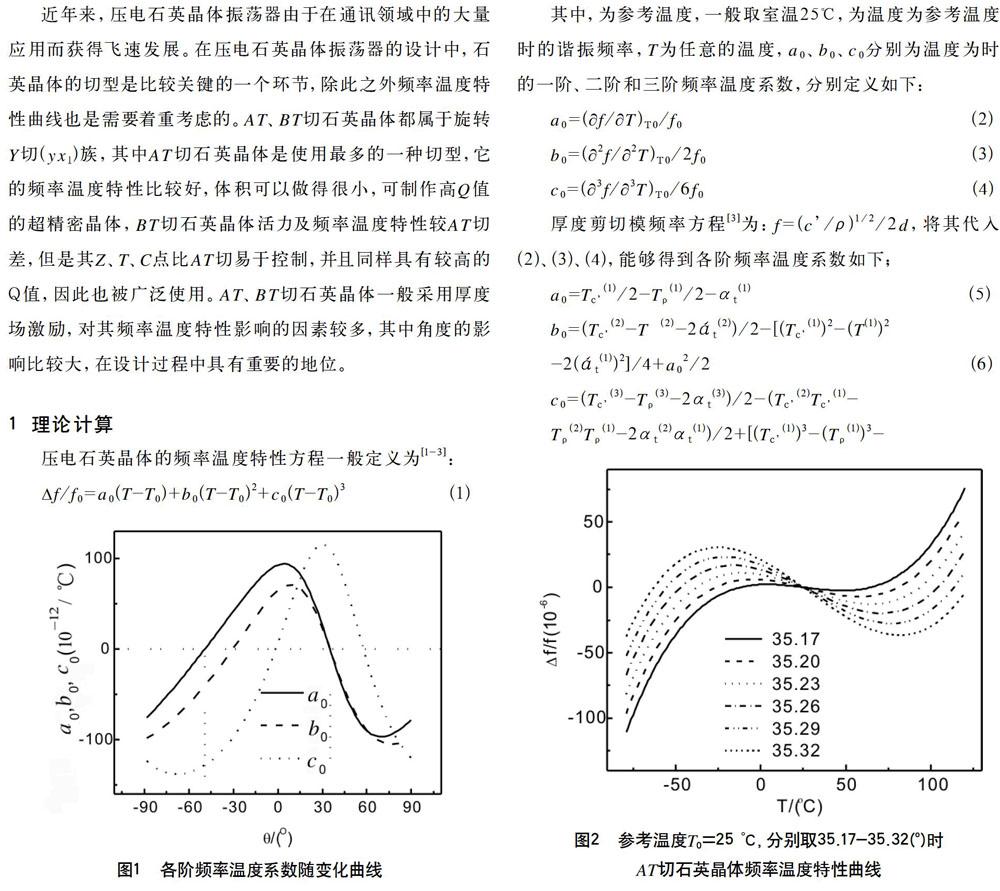
首先计算旋转Y切（yxl）族各阶频率温度系数随角的变化曲线，如图1所示。可以看出，一阶频率温度系数在θ取值为-49和35.2（o）时存在零点值，这两个角度分别对应BT和AT切型的角的切割角度。在θ=35.2（o）附近，一阶频率温度系数和二阶频率温度系数的曲线重叠。θ=35.2（o）处，一阶频率温度系数和二阶频率温度系数都为零，三阶频率温度系数不为零，这表明：θ=35.2（o）附近切割的石英晶体的频率温度特性曲线应表现为三次函数曲线的形式。在θ=-49（o）附近一阶频率温度系数为零，二阶频率温度系数和三阶频率温度系数均不为零，这表明：在θ=-49（o）附近切割的石英晶体的频率温度特性曲线应表现为二次函数曲线的形式。

图2为参考温度T0=25 ℃时，θ取35.17，35.20，35.23，35.26， 35.29，35.32（o）时AT切石英晶体的频率温度特性曲线。从图2可以看出温度特性曲线表现为典型的三次函数曲线形式，这与图1的分析是一致的，此外，频率温度特性曲线随角度变化表现敏感，对同一温度：实际温度小于参考温度情况下，θ角的增大导致频率温度特性曲线正向漂移，实际温度大于参考温度情况下，角的增大导致频率温度特性曲线负向漂移。

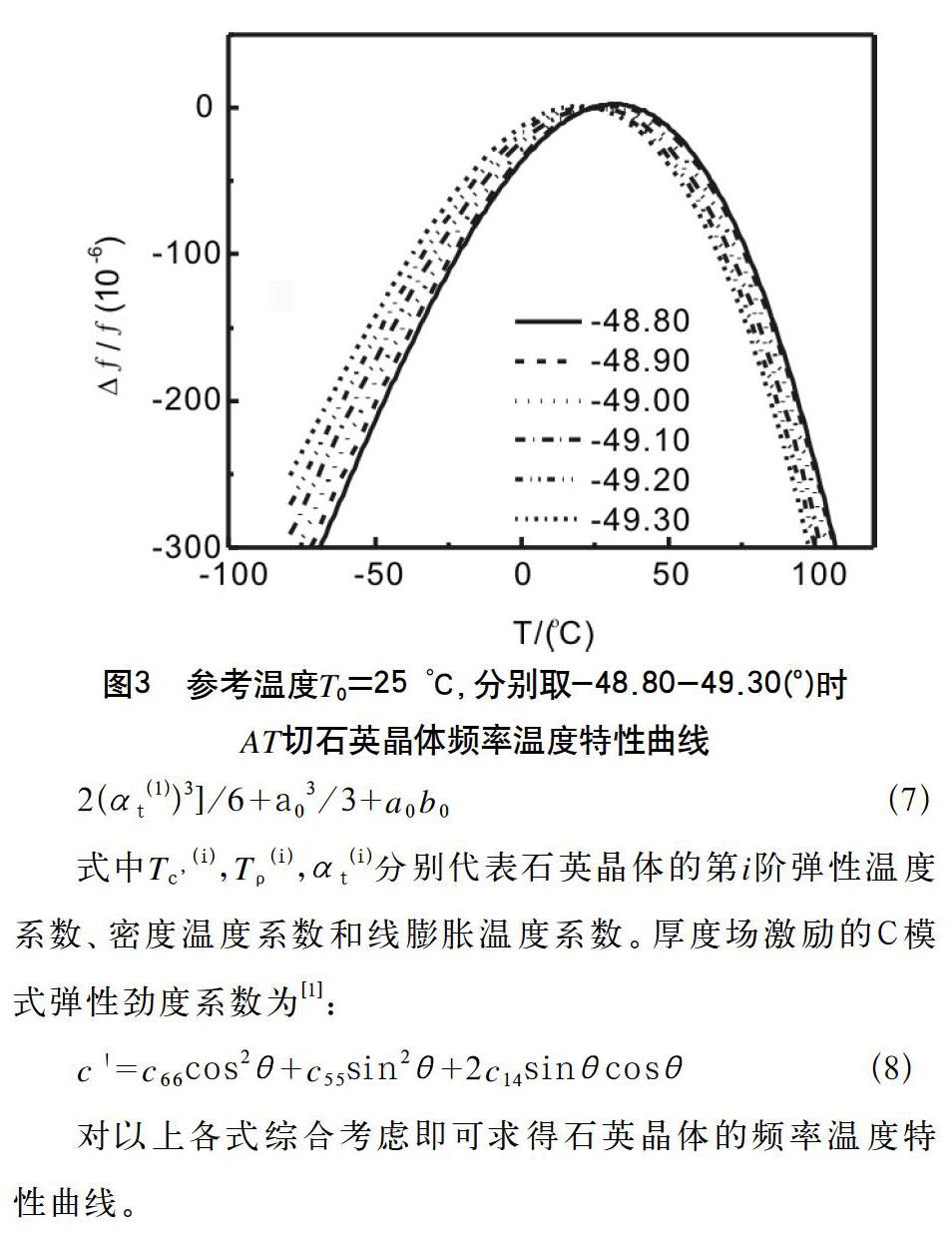
图3为参考温度T0=25℃时，θ分别取-48.80，-48.90，

-49.00，-49.10，-49.20，-49.30（o）时BT切石英晶体的频率温度特性曲线。从图3可以看出BT切石英晶体的温度特性曲线主要表现为二次函数的形式。与AT切相比，θ角变化对频率温度曲线的影响减弱。此外，类似于AT切，对同一温度：实际温度小于参考温度情况下，θ角的增大导致频率温度特性曲线正向漂移，实际温度大于参考温度情况下，θ角的增大导致频率温度特性曲线负向漂移。

3 结语

对广泛应用的旋转Y切（yxl）族的石英晶体的各阶频率温度特性系数进行了计算，结果表明一阶频率温度系数在和存在零点值。以AT和BT切石英晶体为例计算了AT和BT切石英晶体的温度特性曲线，研究发现，AT和BT切频率温度特性曲线随θ角变化有规律的变化，这在石英晶体的设计中具有非常重要的指导价值。

参考文献

[1] 秦自楷.压电石英晶体[M].北京：国防工业出版社，1980： 163-169.

[2] 王文炎，张超，张志甜，等.横向场激励的BT-切石英传感器研究[J].压电与声光，2010，32（2）：265-267.

[3] Mateescu I，Zelenka J，Nosek J，et al.Frequency-Temperature characteristics of the Langasite resonators [C]//Frequncy Control Symposium and PDA Exhibition.2001.