压电半球谐振陀螺的数字检测方法
2016-05-14汪濙海张卫平孙殿竣唐健成宇翔刘亚东邢亚亮
汪濙海 张卫平 孙殿竣 唐健 成宇翔 刘亚东 邢亚亮

摘 要: 提出了一种压电半球谐振陀螺的数字检测方法。该检测方法基于Cyclone IV FPGA开发板,结合AD9226的A/D采样功能和Matlab的数字信号处理能力,实现了对采用压电效应、柯氏效应的压电半球谐振陀螺的输出信号进行采集及检测。介绍了该陀螺的结构和工作原理,并以其工作在89.4 kHz的体声波二波腹模态下的仿真结果为基础设计了数字检测方法。
关键词: 压电; 半球陀螺; FPGA; 数字检测
中图分类号: TN911.72?34 文献标识码: A 文章编号: 1004?373X(2016)09?0145?04
Abstract: A digital detection method for the piezoelectric hemispherical resonator gyro is presented. This detection method is based on Cyclone IV FPGA development board, and combines the A/D sampling function of AD9226 with digital signal processing ability of Matlab to acquire and detect the output signal of the piezoelectric hemispherical resonator gyro with piezoelectric effect and Coriolis effect. The structure and working principle of the gyro are introduced. The digital detection method was designed based on the simulation result that the gyro works at bulk acoustic wave 2 antinode modal of 89.4 kHz.
Keywords: piezoelectricity; hemispherical gyro; FPGA; digital detection
0 引 言
半球谐振陀螺仪[1]是一种集高检测精度、高可靠性及稳定性、良好的抗冲击性能和长使用寿命等多种优势于一体的哥式振动陀螺仪[2]。其随机漂移为10-4 (°)/hr量级,使用寿命能达到15年[3]。在航空航天领域有着特殊的优势和使用前景。其工作原理为采用半球壳唇缘的径向振动驻波进动效应,结合柯氏效应检测输入角速度[1]。
FPGA作为与DSP齐名的嵌入式开发处理器,是在可编程器件的基础上发展而来的产物。其最具代表性的两大特色是开发的灵活性和并行的程序处理能力。由于它具有上述两大优势,非常适合需要多样算法和进行并行计算的数字处理任务。
本文针对压电半球谐振陀螺仪,介绍了陀螺的结构和工作原理,并选择了其在89.4 kHz下的二波腹模态作为工作模态进行仿真,最后基于Cyclone IV FPGA开发板、AD9226芯片和Matlab程序,设计出了陀螺的数字检测方法。
1 陀螺基本结构
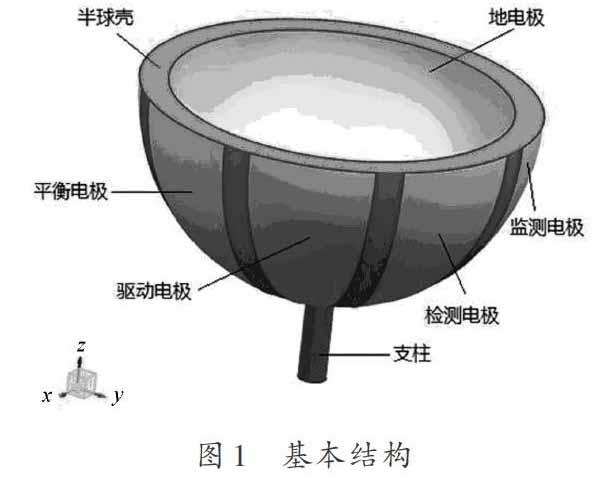
压电半球谐振陀螺分为压电半球体,支柱,表面电极,如图1所示。
出于原理及设计上考虑,半球壳的材料为PZT压电材料,支柱为金属材料,电极为金属镍。支柱接合在半球壳中心,半球壳内表面覆盖了一层地电极,半球壳外表面均匀分布了4组8个外电极,依次为驱动电极、检测电极、监测电极、平衡电极。8个电极对向成组为同名电极,同时相邻电极分布上互差45°,其间相隔5°,如此分布可令陀螺获得对称的工作模态,有利于驱动及检测。
2 陀螺工作原理
通过模态仿真分析,压电半球谐振陀螺主要工作在如图2所示的体声波简并模态下。
同时使用频谱分析仪测量陀螺的频响曲线,结合仿真结果推定陀螺的工作频率,即谐振频率为89.4 kHz。
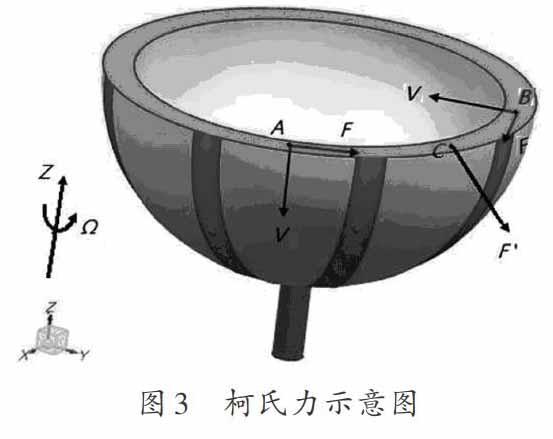
通过在图1所示的陀螺的一对驱动电极上施加该频率的正弦信号,由压电材料半球壳的逆压电效应可以将陀螺激振到如图2(a)所示的驱动模态下。由于电信号呈正弦变化,在半球壳上将有两个频率相同的波朝相反的方向行进因此产生干涉效应,形成体声波驻波。上述振动形式是压电半球谐振陀螺的参考振动。此时若有沿半球壳轴向(z轴方向)的角速度输入,如图3所示,则由柯氏力效应及其公式:F=2m·VXΩ可知,参考振动下的波腹点A,B的振动速度V和所受的柯氏力F状况如图3所示,并且C点即参考振动的波节点,由于柯氏力合成力F′的作用将被激振起如图2(b)所示的检测模态下的振动。检测模态的振动幅度与柯氏力的大小成正比,因此也和输入的角速度成正比。
这种被激振起的检测模态振动和驱动模态下的振动模式相似,而驱动模态和检测模态驻波的波腹和波节点互相相反,故驱动模态与检测模态的振动几乎不互相干扰[4]。
至此,压电半球壳上的检测电极处由于压电效应将输出一正弦的电信号,此电信号的大小与输入角速度大小成正比,因此只要处理此电信号便能得到输入角速度的大小。
3 陀螺检测框架
基于上述压电半球谐振陀螺的工作原理,如果要通过一套电路系统检测外部输入的角速度,应当将电路系统分为驱动电路,输出接口电路,检测电路[5],如图4所示。
驱动电路部分主要提供一个频率稳定的正弦信号,并将其加载到陀螺的一对驱动电极上,将陀螺激振到驱动模态下。输出接口电路的作用是将陀螺输出电极上的电荷信号转换成符合使用要求的信号,并提供可供后续处理使用的相关接口。检测电路的目标是将从陀螺上得到的信号进行处理,用最终得到的信号表征输入陀螺的外部角速度[6]。
在压电半球谐振陀螺电路系统的实际设计制作中,陀螺的驱动电路采用以锁相环为核心的模拟电路加以实现[7],输出接口电路由将电荷信号转化为电压信号的电荷放大器模块和为了便于后续处理而设计的直流偏置电路组成[8]。考虑到陀螺输出信号的复杂性以及角速度检测所需的实时性,再综合考虑同种类陀螺的后续研究,采用能并行处理信号,同时有高速处理信号能力的FPGA系统对陀螺的输出信号进行处理不失为一种合适的方法。
4 陀螺检测方法
考虑到陀螺制造过程中不对称性等原因带来的影响,若输入陀螺的驱动信号为[Asin(ωt)],则在检测电极处输出接口输出的信号为一由与驱动信号同频的载波信号和由柯氏效应产生的信号叠加所产生的信号[Dsin(ωt)+CΩcos(ωt)]。为了检测上述信号中的[Ω,]采用如下方法:由于平衡电极和检测电极的输出信号中载波分量相位、频率相同,而由柯氏效应产生的信号频率相同,相位相差180°,所以在平衡电极处输出接口输出的信号为[Esin(ωt)-FΩcos(ωt),]将上述两信号进行检波差分去除共模部分,便可得到含[Ω]差模放大部分信号[GΩcos(ωt)]。再将此信号与调相过的驱动信号或是与驱动信号同频率的监测电极处输出接口输出的信号进行乘法解调,就可以得到[GΩcos(ωt)?Hcos(ωt)=][Jcos2(ωt)-IΩ,]最后通过低通滤波的方法就可以得到[Ω]的大小。而在实际测试中,平衡电极处和检测电极处的输出信号中载波分量相位会有一定的角度差,所以需要进行调相,整个信号处理的流程如图5所示。
设计离散化的数据处理方案如下:由于AD9226输入范围为-5~5 V,需要控制采样信号的幅值,并设定采样频率为50 MHz,将检测电极信号、平衡电极信号和监测电极信号的数据点进行采集,分别保存在Sen[],Bal[],Det[]三个数组中。考虑到算法的实时性,采用精度较低但耗时较短的检波及调相算法:在初始化阶段,输入角速度为0,此时Sen[],Bal[]两数组中的信号仅为载波信号。分别求出两数组中前一个周期数据点中的最大值Max1,Max2和在数组中所在的位置[p1,p2,]将Bal[]数组对Sen[]数组进行归一化处理,并将Bal[]数组中数据的位置进行平移使其最大值位置[p2]与[p1]对齐,最后进行差分得到新数组Dec[]。在有角速度输入的测试阶段,按上述方法进行信号处理就能有效地去除共模载波信号。另一方面,求出Det[]数组前一个周期数据点中最大值Max3和最小值Min3在数组中的位置[p3,p4,]通过平移数组Det[]中数据的位置,将上述两位置的中间位置[p5]与[p1]重合,并将之与Dec[]中的数据相乘,得到解调信号数组Mul[]。最后用窗函数对数组Mul[]进行低通滤波[9?10],就可以得到与[Ω]大小正比例相关的数据。
上述处理算法中,在调相的过程中,由于检测到的最大值不一定是实际信号的最大值,所以在调相的过程中可能产生两实际信号的调相误差。考虑[p1]与[p2]位置相差[θ,][p1]与[p5]位置相差[λ,]即检测电极信号为[Dsin(ωt)+CΩcos(ωt)]时,平衡电极信号为[Esin(ωt+θ)-][FΩcos(ωt+θ),]与差分信号相乘的信号为[Hcos(ωt+λ)],最后滤波后的信号为[a4+a5Ω,]其中[a4,][a5]均为与[θ]和[λ]相关的常数,也就是说,如果[θ]和[λ]的值不变,调相过程存在的误差并不影响最终的检测结果。
5 陀螺检测结果
6 结 论
本文提出了一种压电半球谐振陀螺的数字检测方法。该检测方法基于Cyclone IV FPGA开发板、AD9226芯片和Matlab程序,实现了对采用压电效应、柯氏效应的压电半球谐振陀螺的输出信号进行采集及检测。本文介绍了陀螺的结构和工作原理,并以其工作在89.4 kHz的体声波二波腹模态下的仿真结果为基础设计了数字检测方法。
参考文献
[1] LYNCH D D. Hemispherical resonator gyro [C]// Proceedings of 1984 IEEE Inertial Technology for the Future Conference on Aerospace Electronic Systems. [S.l.]: IEEE, 1984, 20(4): 414?444.
[2] L? Z Q. Coriolis vibratory gyros [J]. Piezoelectric & acoustooptics, 2004(2): 38?42.
[3] ROZELLE D M. The hemispherical resonator gyro: from wineglass to the planets [C]// Proceedings of 19th AAS/AIAA Space Flight Mechanics Meeting. [S.l.]: AAS/AIAA, 2009: 1157?1178.
[4] 张弓,张卫平,许仲兴,等.摇摆质量增强压电体声波固体波动圆盘微陀螺[J].振动与冲击,2014(19):104?108.
[5] GREGORY J A, CHO J, NAJAFI K. MEMS rate and rate?integrating gyroscope control with commercial software defined radio hardware [C]// Proceedings of 2011 16th International Conference on Solid?State Sensors, Actuators and Microsystems. Beijing, China: IEEE, 2011: 2394?2397.
[6] 李兰飞.基于DSP的MEMS陀螺信号采集与处理系统设计[D].哈尔滨:哈尔滨工程大学,2009.
[7] 刘吉超,杜力坤·苏来曼,闫相东.锁相环集成电路NE564原理及应用[J].新疆师范大学学报(自然科学版),2009(4):65?68.
[8] 杨宪.用集成运算放大器构成电荷放大器组件[J].电子技术应用,1993(12):41?42.
[9] 潘玉恒,鲁维佳,王悦.基于Matlab和DSP实现的FIR数字低通滤波器[J].黑龙江科技信息,2007(18):92.
[10] 陈雁.用Matlab设计及FPGA实现FIR滤波器的方法[J].计算机仿真,2003(12):144?146.
