基于传递路径分析的激励对汽车平顺性的影响

潘道远，王　刚，唐　冶

(1.安徽工程大学 机械与汽车工程学院，安徽 芜湖　241000；

2.芜湖禾丰离合器有限公司博士后工作站，安徽 芜湖　241000)



基于传递路径分析的激励对汽车平顺性的影响

潘道远1，王刚2，唐冶1

(1.安徽工程大学 机械与汽车工程学院，安徽 芜湖241000；

2.芜湖禾丰离合器有限公司博士后工作站，安徽 芜湖241000)

摘要：为研究发动机激励与路面激励对汽车平顺性的影响，建立了包含悬置系统和悬架系统的车辆13自由度数学模型，给出了发动机和路面激励模型，提出了基于TPA的汽车平顺性分析方法。在仿真计算基础上进行了实车试验，计算与试验结果基本吻合，验证了所建立模型的正确性。结合各挡位车速与发动机转速之间的对应关系，分析了不同激励对汽车平顺性的影响。结果表明：发动机激励对汽车平顺性的影响小于路面激励，但不容忽视。

关键词：发动机激励；路面激励；车辆模型；平顺性

汽车行驶平顺性是汽车性能的一个重要评价指标。随着市场用户需求的提升以及现代汽车技术的发展，人们对汽车行驶平顺性提出了更高要求。通常，对于汽车行驶平顺性主要研究25 Hz以下的振动。因此，在建立汽车的简化振动模型时仅考虑随机路面激励，忽略了发动机激励对整车振动的影响[1-3]。实际上，随着车速的提高，发动机激励对汽车平顺性的影响不容忽视[4]。目前，在利用传递路径分析法TPA(transfer path analysis)研究激励对汽车行驶平顺性影响方面已经取得了很多成果。文献[5]研究了动力总成振动对整车行驶平顺性的传递路径；文献[6]研究了路面激励对汽车行驶平顺性影响的传递路径。但上述方法都是采用实车试验采集数据，然后通过国外软件LMS/TPA进行分析，因此无法在汽车产品设计的初期阶段提供发动机激励与路面激励对汽车振动性能的影响。本文在汽车设计阶段通过仿真研究发动机激励与路面激励对整车平顺性的影响，为车辆结构的优化设计提供相关理论依据，具有十分重要的理论与工程价值。

1车辆13自由度数学模型

汽车悬置系统将动力总成和车架弹性连接，用于承受动力总成重量及隔离振动传递。汽车悬架系统是车辆系统中的关键子系统，起到传递和衰减路面激励的作用，能改善行驶平顺性。因此，为了研究发动机激励与路面激励对汽车平顺性的影响，建立含悬置系统和悬架系统的车辆13自由度数学模型(见图1)。设汽车质量集中在质心处，取质心为坐标原点，前进方向为X轴正方向，水平向左为Y轴正方向，过质心垂直向上为Z轴正方向。

定义整车系统的13个广义变量为

(1)

其中：qi= [xyz]T为动力总成广义坐标；qj= [zbφθ]T为车身广义坐标；qu= [z1z2z3z4]T为簧下质量广义坐标。

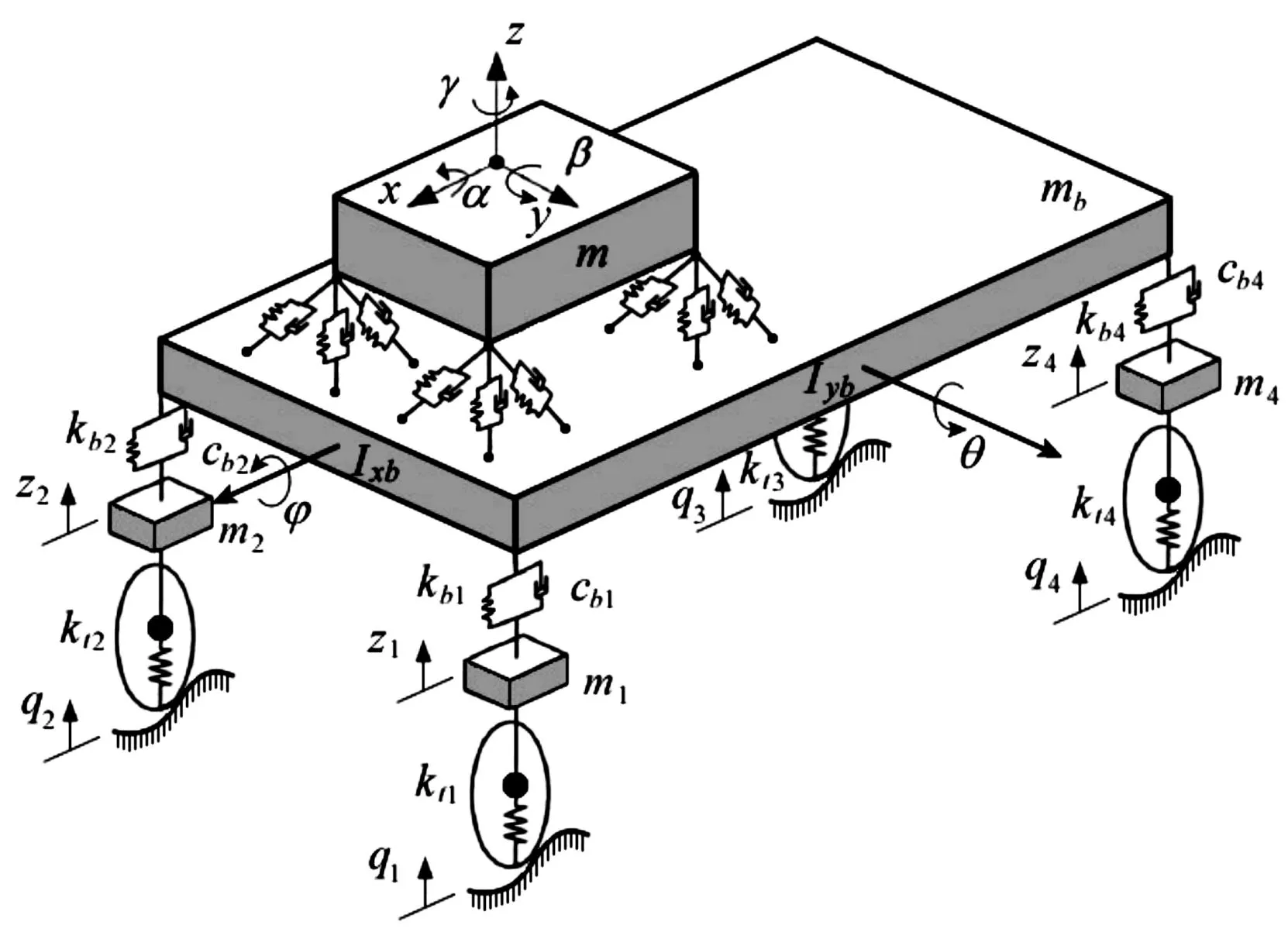
图1　车辆13自由度模型

车辆系统振动时的动能可以通过式(2)求得。

(2)

其中：mj= diag(mbIxbIyb)，mu= diag(m1m2m3m4)

式中：Ixx，Iyy和Izz为动力总成的转动惯量；Ixy，Ixz和Iyz为动力总成的惯性积。

假设动力总成与车身通过n个弹性悬置元件连接。各悬置元件可简化为三向相互垂直的线性弹簧与粘性阻尼元件，局部坐标系统G-uvw分别表示悬置的3条弹性主轴方向[7]。kp= diag(kupkvpkwp)为悬置p的刚度矩阵，其中kup，kvp和kwp为主刚度；cp= diag(cupcvpcwp) 为悬置p的阻尼矩阵，其中cup，cvp和cwp为主阻尼。悬置p在动力总成i上的连接点为Pi。Pi在动力总成局部坐标系下的坐标为(xpi，ypi，zpi)，则Pi点的位移可表示为Bpiqi。悬置p在车身j上的连接点为Pj。Pj在车身局部坐标系下的坐标为(xpj，ypj，zpj)，则Pj点的位移可表示为Bpjqj。因此，悬置p在整车坐标系下的弹性变形[8]为

(3)

其中：

悬置p的局部坐标系Gp-upvpwp在动力总成坐标系Oi-xyz中的方向余弦矩阵为Tp，则悬置p在其局部坐标系Gp-upvpwp的弹性变形为

(4)

其中up= [ΔupΔvpΔwp]T。

根据整车系统耗散能的定义可得

(5)

将式(4)代入式(5)，可改写为

(6)

其中：Bl=I4；cb= diag(cb1cb2cb3cb4)；

同理，整车系统势能为

(7)

其中：kb= diag(kb1kb2kb3kb4)；kt= diag(kt1kt2kt3kt4)。

将系统动能E、耗散能D和势能V代入拉格朗日方程，可得整车系统动力学方程：

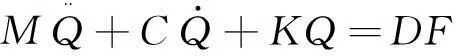
(8)

其中：M为系统质量矩阵；C为系统阻尼矩阵；K为系统刚度矩阵；D为系统扰动矩阵；F= [FiFu]T为系统所受激励，Fi为发动机激励，Fu为路面激励。

2车辆激励模型

在汽车正常行驶过程中，来自发动机汽缸内的燃气压力和运动部件产生的不平衡惯性力与力矩激励车辆不断产生振动[9]。直列四缸发动机激励可简化为

(9)

其中：Fy= sinψ·4msrλω2cos2ωt；Fz=cosψ·4msrλω2cos2ωt；Mx=M0(1+1.3sin2ωt)；My=Fz·A，My=Fz·A。式中：ψ为动力总成的安装角；ms为单缸活塞和往复运动部件的质量；r为曲柄半径；λ为曲柄半径与连杆长度之比；ω为发动机曲轴转动角速度；A为二、三缸中心线至动力总成质心的水平距离；M0为发动机输出扭矩。

路面激励模型用滤波白噪声的时域表达式[10]来描述：

(10)

式中：f0为滤波器的下限截止频率；n0为参考空间频率；Gq(n0)为路面不平度系数；w(t)为高斯白噪声；v为汽车行驶速度。

3基于TPA的平顺性分析

发动机激励与路面激励通过不同的路径经过衰减传递到车身。利用傅里叶变换，将激励力从时域变为频域：

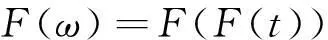
(11)

以车身垂直加速度为例，根据传递路径分析法，车辆系统为线性非时变系统时，车身垂直振动等于发动机激励和路面激励传递到车身的能量叠加，则发动机激励对车身垂直振动的贡献量Ti(ω)和路面激励对车身垂直振动的贡献量Tu(ω)为：

(12)

式中：Hj/k(ω)为激励k对车身j垂直振动的频响函数；fk(ω)为发动机激励和路面激励的激励分量；Fi(ω)为发动机激励分量；Fu(ω)为路面激励分量；Hi(ω)为发动机激励对车身垂直振动的频响函数矩阵；Hu(ω)为路面激励对车身垂直振动的频响函数矩阵。频响函数矩阵Hi(ω)和Hu(ω)通过对整车系统动力学方程式(8)进行拉氏变换即可得到。

汽车行驶平顺性评价指标一般以时间历程为基础。因此，对式(12)进行傅里叶逆变换，将贡献量Ti(t)和Tu(t)从频域转化为时域：

(13)

按式(14)计算贡献量时间历程的均方根值。

(14)

式中：T为振动的时间历程；ai为发动机激励对汽车车身垂直振动的影响；au为路面激励对汽车车身垂直振动的影响。

4模型仿真与试验

以某车型为例，利用Matlab/Simulink建立汽车平顺性仿真模型，如图2所示。确定相关的参数值，设定发动机转速、汽车行驶速度和路面等级，然后进行仿真分析。

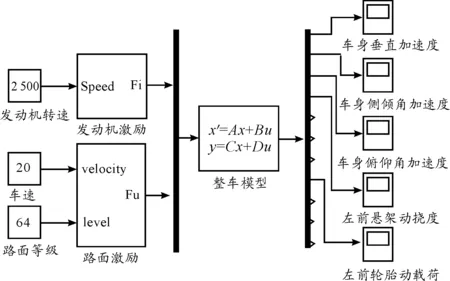
图2　汽车平顺性仿真模型

4.1计算参数

为了验证所建模型的有效性，利用Matlab编写仿真计算程序。模型参数值分别为：动力总成质心坐标为(1.4 m，-0.02 m，0.14 m)，车身质心坐标为(0 m，0 m，0 m)，m=168.8 kg，Ixx=14.036 6 kg·m2，Iyy=5.819 1 kg·m2，Izz=10.579 7 kg·m2，Ixy=0.394 kg·m2，Ixz=0.428 kg·m2，Iyz= 0.155 kg·m2，mb=830.2 kg，Ixb= 264.7 kg·m2，Iyb=1 658.5 kg·m2，m1=m2=35 kg，m3=m4=28 kg，kb1=kb2=17 000 N/m，kb3=kb4=23 kN/m，cb1=cb2=1 900 N·s/m，cb3=cb4= 2 300 N·s/m，a1=1.35 m，a2=1.75 m，b1=0.75 m，b2=0.8 m，kt1=kt2=kt3=kt4= 200 kN/m。本文所研究车型的动力总成为3点悬置，所有悬置安装角度均为零。

4.2结果分析

取发动机转速为3 000 r/min、车速为80 km/h的B级路面输入进行仿真分析。设定仿真时间为5 s，选取车身垂直加速度、悬架动挠度和轮胎动载荷为评价指标。定义发动机和路面双重激励为联合激励。分别以联合激励、路面激励和发动机激励对汽车平顺性的影响进行分析，部分仿真结果如图3～6所示。

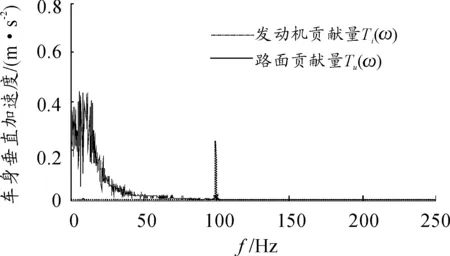
图3　激励对车身垂直加速度的贡献量

由图3可知：路面激励的贡献量主要体现在低频区，一般在25 Hz内，而发动机激励的贡献量体现在高频区，其贡献量的峰值与发动机转速有关。由图4～6可知：路面激励对车身垂直加速度、悬架动挠度和轮胎动载荷的影响大于发动机激励。发动机激励对车身垂直加速度有一定影响，但传递到悬架系统和轮胎时，振动基本被隔离。因此，对于发动机激励，悬架系统和轮胎主要承受的是其静载荷。

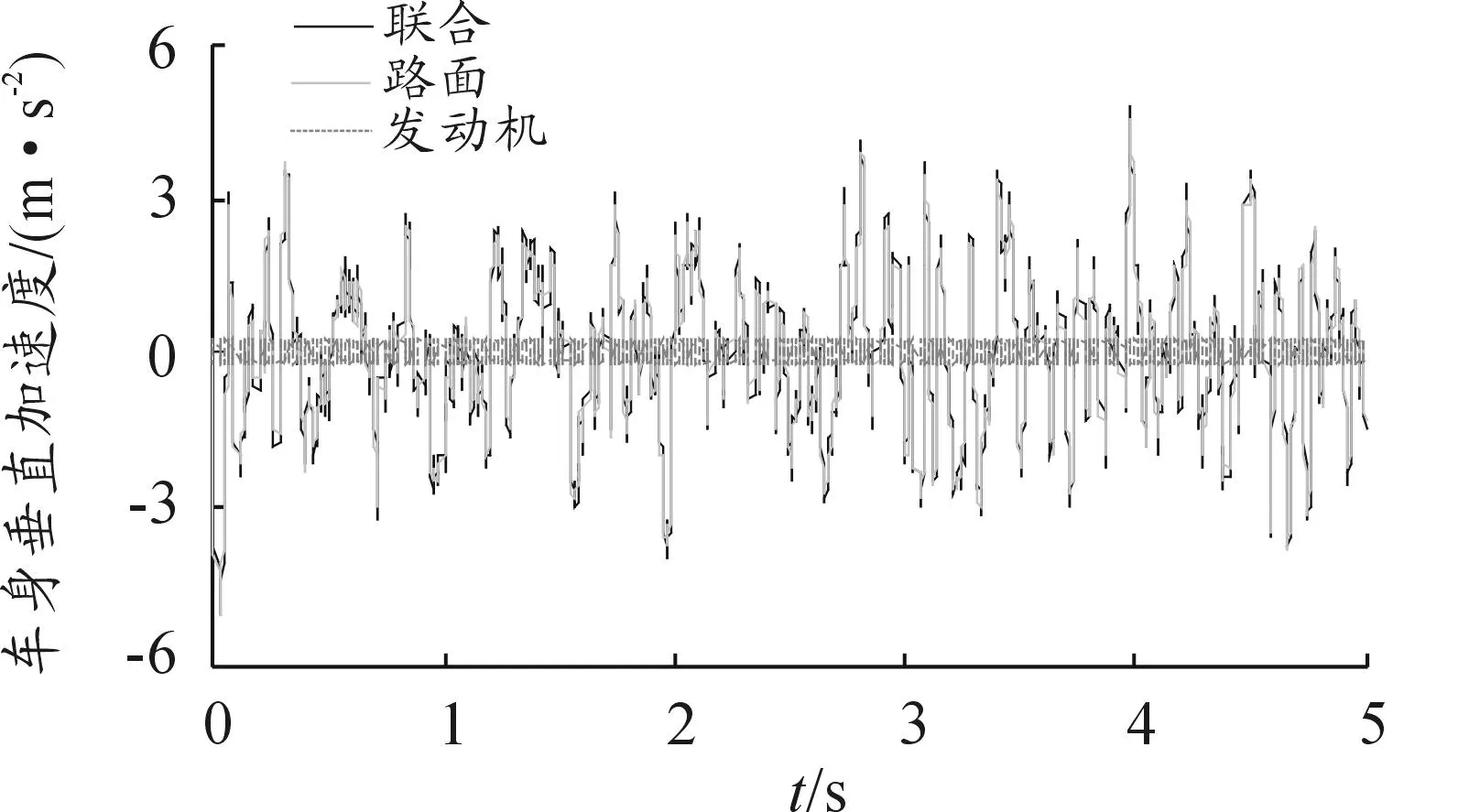
图4　车身垂直加速度

为验证模型的正确性进行了实车试验，如图7所示。其中路面激励由4通道道路模拟试验系统提供。仿真计算结果与实车试验结果如表1所示。从表中可以看出：仿真与试验结果基本吻合，验证了模型的有效性和正确性。

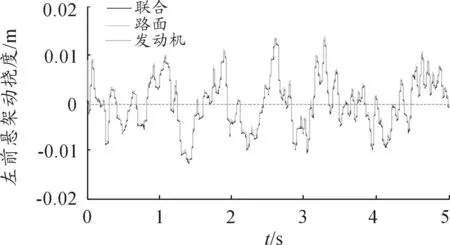
图5　左前悬架动挠度

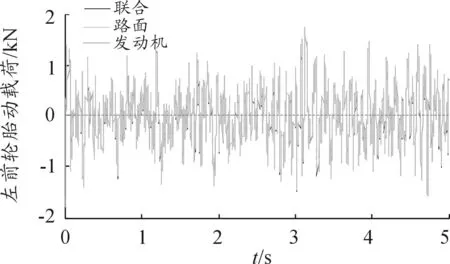
图6　左前轮胎动载荷

图7　实车试验

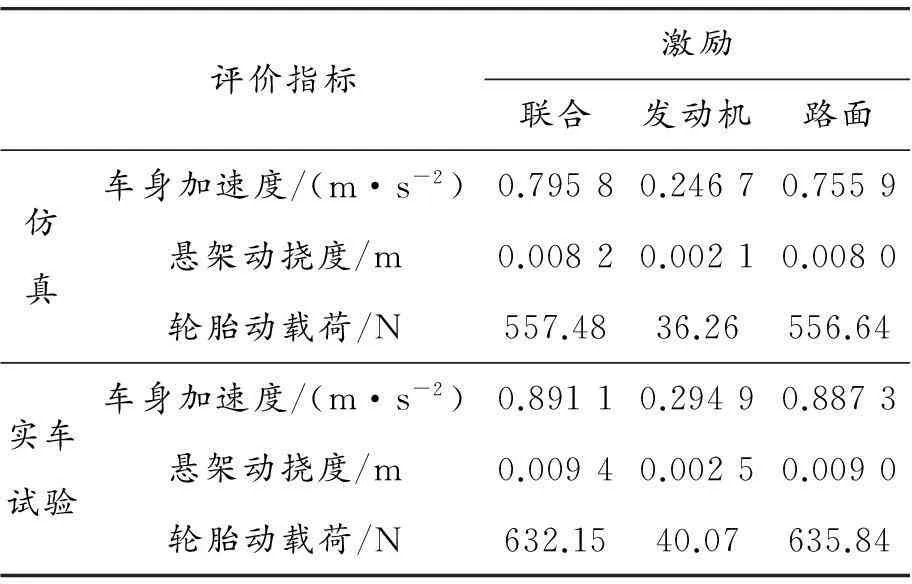
评价指标激励联合发动机路面仿真车身加速度/(m·s-2)0.79580.24670.7559悬架动挠度/m0.00820.00210.0080轮胎动载荷/N557.4836.26556.64实车试验车身加速度/(m·s-2)0.89110.29490.8873悬架动挠度/m0.00940.00250.0090轮胎动载荷/N632.1540.07635.84

为了进一步研究激励对汽车行驶平顺性的影响，结合各挡位车速与发动机转速之间的对应关系(如表2所示)，根据基于TPA的平顺性分析方法，计算了发动机激励与路面激励对车身振动的影响，结果如表3所示。

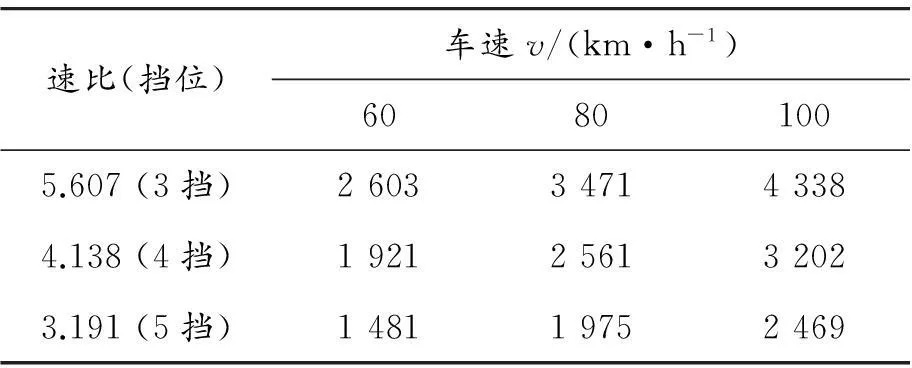
表2　各挡车速与发动机转速的对应关系

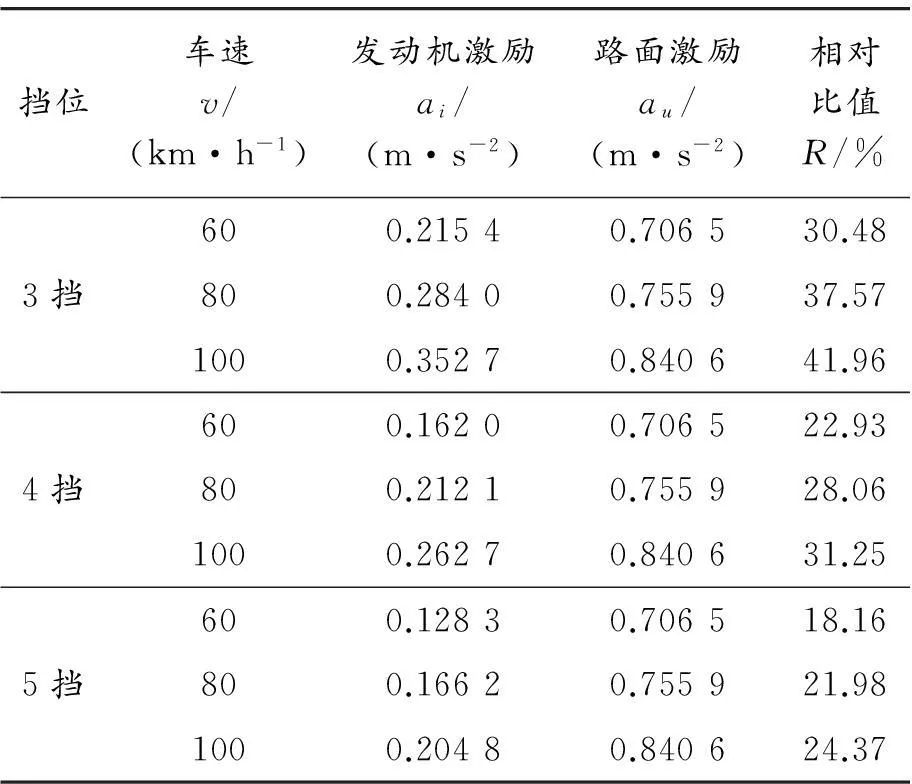
表3　发动机激励与路面激励对车身振动影响的对比

由表3可知：在相同挡位条件下，随着车速提高，发动机激励与路面激励对车身振动的影响也随之上升，但发动机激励影响的上升速度高于路面激励影响的上升速度。在4挡条件下，当车速由60 km/h 上升到100 km/h时，发动机激励影响与路面激励影响的比值由22.93%上升为31.25%。在相同车速条件下，挡位越高，发动机激励影响越小，而路面激励影响不变，因为路面激励只与路面等级和车速有关。当车速为80 km/h，挡位由3挡上升为4挡时，发动机激励对车身振动的影响由0.284 0 m·s-2下降为0.212 1 m·s-2，而路面激励对车身振动的影响仍为0.755 9 m·s-2。因此，发动机激励影响与路面激励影响的比值由37.57%下降为28.06%。

5结束语

基于车辆13自由度数学模型和车辆激励模型，提出了基于TPA的汽车平顺性分析方法，并进行了仿真计算与实车试验。结果表明：建立的包含悬置系统和悬架系统的车辆13自由度数学模型正确、可靠，提出的基于TPA的汽车平顺性分析方法合理。对于汽车平顺性的影响，发动机激励小于路面激励，但不容忽视。在相同挡位条件下，随着车速提高，发动机激励与路面激励对车身振动的影响也随之上升，但发动机激励影响的上升速度高于路面激励影响的上升速度。在相同车速条件下，路面激励影响不变，挡位越高，发动机激励影响越小。

参考文献：

[1]余志生.汽车理论(第5版)[M].北京:机械工业出版社,2011.

[2]UYS P E,ELS P S.Suspension settings for optimal ride comfort of off-road vehicles traveling on roads with different roughness and speeds[J].Journal of Terramechanics,2007,44:163-175.

[3]雷良育,周晓军.基于虚拟样机技术的汽车平顺性仿真分析[J].传感技术学报,2006,19(6):2646-2649.

[4]潘道远,高翔,夏长高,等.典型工况下动力总成悬置系统动态振动位移分析[J].机械设计与研究,2013,29(3):18-22.

[5]王登峰,李未,陈书明,等.动力总成振动对整车行驶平顺行的传递路径分析[J].吉林大学学报(工学版),2011,41(9):92-97.

[6]李未,王登峰,陈书明,等.路面激励对汽车行驶平顺行影响的传递路径分析[J].吉林大学学报(工学版),2011,41(5):1193-1198.

[7]范让林,吕振华.汽车动力总成三点式悬置系统的设计方法探讨[J].汽车工程,2005,27(3):304-308.

[8]DE S,CLARENCE W.Vibration and Shock Handbook[M].BocaRaton:CRC Press,2005.

[9]时培成.汽车动力总成悬置系统隔振分析与优化研究[D].合肥:合肥工业大学,2010.

[10]陈士安,邱峰,何仁,等.一种确定车辆悬架LQG控制加权系数的方法[J].振动与冲击,2008,27(2):65-68.

(责任编辑刘舸)

Influence of Excitation on Vehicle Ride Comfort Based on Transfer Path Analysis

PAN Dao-yuan1, WANG Gang2, TANG Ye1

(1.School of Mechanical and Automotive Engineering,Anhui Polytechnic University, Wuhu 241000, China;2.Postdoctoral Center of Wuhu Hefeng Clutch Co., Ltd., Wuhu 241000, China)

Abstract:In order to explore the influence of the engine excitation and the road excitation on the ride comfort for vehicle, a full vehicle model with 13 freedom degrees containing the mounting system and the suspension system was established, and the engine excitation and the road excitation were introduced. The method of the ride comfort for vehicle based on TPA was derived. On the basis of the simulation calculating, the road test of actual vehicle was conducted. The results of simulation calculating and experiment result were consistent, which proved the correctness of this model. Based on the corresponding relationship between vehicle speed and engine speed in different gears, the ride comfort for vehicle under different excitation was analyzed. The results indicate that the influence of the road excitation is less than the engine excitation on the ride comfort for vehicle, but its influence cannot be ignored.

Key words:engine excitation; road excitation; vehicle model; ride comfort

中图分类号：U461.4

文献标识码：A 1674-8425(2016)03-0016-06

doi:10.3969/j.issn.1674-8425(z).2016.03.003

作者简介：潘道远(1982—)，男，博士，讲师，主要从事汽车电子、振动分析与控制研究。

基金项目：国家自然科学基金资助项目(51575001)；安徽省高等学校自然科学研究项目(TSKJ2015B01)；安徽工程大学科研启动基金项目(2015YQQ002，2015YQQ003)

收稿日期：2015-11-22

引用格式：潘道远，王刚，唐冶.基于传递路径分析的激励对汽车平顺性的影响[J].重庆理工大学学报(自然科学)，2016(3):16-21.

Citation format：PAN Dao-yuan, WANG Gang, TANG Ye.Influence of Excitation on Vehicle Ride Comfort Based on Transfer Path Analysis[J].Journal of Chongqing University of Technology(Natural Science)，2016(3):16-21.