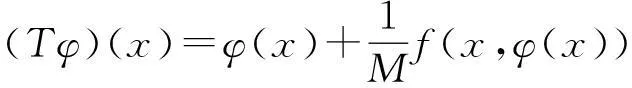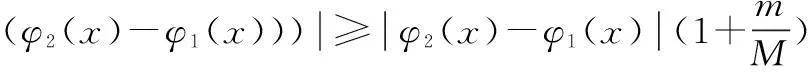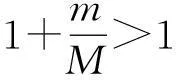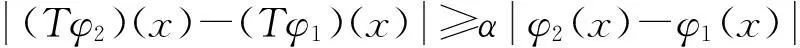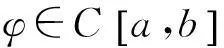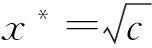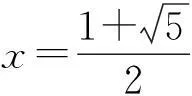扩张映射原理及其应用

柳彦军

(重庆第二师范学院 数学与信息工程系，重庆 400067)



扩张映射原理及其应用

柳彦军

(重庆第二师范学院 数学与信息工程系，重庆 400067)

摘要：为了完善和发展不动点定理及其应用, 本文给出扩张映射的概念, 并利用Banach压缩映射原理证明扩张映射原理, 进一步得到其他一些不动点定理。最后, 详细论述扩张映射原理在证明方程解的存在性, 求一些数列极限和判定函数是否有不动点定理的应用。

关键词：Banach压缩映射原理；扩张映射原理；不动点；解的存在性

Banach压缩映射原理在数学的各个分支中起着非常重要的作用, 被广泛应用于非线性Volterra积分方程、抽象空间中非线性微积分方程及计算数学中的收敛算法等。另外, Banach压缩映射原理有多种形式的推广, 如伪压缩和集值压缩等[1]。受Banach压缩映射原理的启发, 以逆向思维考察Banach压缩映射原理, 给出扩张映射的定义, 并利用Banach压缩映射原理得到扩张映射原理, 进一步得到其他一些不动点定理。那么, 如同Banach压缩映射原理一样, 扩张映射原理也应该有很重要的应用。

一、 预备知识与引理

定义1[2-4]若

d(Fx,Fy)≤kd(x,y),∀x,y∈X，0

则称F为X上的一个压缩映射。

引理1[2-4](Banach压缩映射原理)设F是完备度量空间(X,d)上的压缩映射.则F在X中有唯一的不动点。

引理2[4]度量空间X到Y中的映射T是X上的连续映射的充要条件为Y中的任意M的原象T-1M是X中的闭集。

引理3[5]设X是完备度量空间, A是X一子集。若f,g:A→X满足下列条件:

(1) f是满射;

(2)存在下半连续函数φ:X→[0,∞)满足条件

d(f(x),g(x))≤φ(f(x)-φ(g(x)),∀x∈A

则f和g有重合点, 即存在x∈A, 使得g(x)=f(x)。

特别地, 若A=X,g=Ix(X上的单位映射), 则f在X中有一不动点。

二、主要结果及其证明

定义2[1]若d(Fx,Fy)≥Ld(x,y),∀x,y∈X,L>1, 则称F为X上的一个扩张映射。

定理1(扩张映射原理)设F是完备度量空间上的扩张映射. 则F在X中有唯一的不动点。

证明由F是扩张映射易知F是单射,从而F-1:F(X)→X存在, 且对任意的x∈F(X)有x=F(F-1(x))。

下证F-1:F(X)→X是压缩映射。事实上，对任意 的x,y∈F(X)，我们有

d(x,y)=d(F(F-1(x)),F(F-1(y)))

≥Ld(F-1(x),F-1(y))。

d(xn,xn+1)=d(F-1(xn-1),F-1(xn))

对任意的正整数p，有

d(xn+p,xn)

≤d(xn+p,xn+p-1)+d(xn+p-1,xn+p-2)+…+d(xn+1,xn)

即{xn}是F(X)中的Cauchy列。

设xn→x*(n→∞), 由F-1的连续性

知F-1(xn)→F-1(x*)(n→∞),又

F-1(xn)=xn+1→x*(n→∞),

故F-1(x*)=x*, 由此得F(x*)=x*. 因F是扩张映射, 唯一性显然。

推论2设X完备度量空间,T:X→X.若存在常数L(L≥1)及正整数n0, 使对任何x,y∈X, 都有d(Tn0x,Tn0y)≥Ld(x,y),则T存在唯一的不动点。

定理2设D是完备度量空间(X,d)上的一个非空闭子集。F:D→F(D)是扩张映射且D⊂F(D), 则F在D中有唯一的不动点。

证明类似于定理1的证明易得F-1:F(D)→D⊂F(D)是压缩映射，从而F-1也是连续映射, 由于D是闭集, 根据引理2知,F(D)也是闭集。由Banach压缩映射原理知, F-1在F(D)中有唯一的不动点, 即存在x*∈F(D), 使得F-1(x*)=x*。而F-1(x*)∈D, 故x*∈D且F(x*)=x*。因F是扩张映射, 唯一性显然。

≤…

于是, 对任意的正整数p, 有

所以{xn}是Cauch列,于是{xn}收敛。

定理4设(X,d)是一完备的度量空间, 映射f:X→X是连续满射, 若存在L>1,使得

d[f2k-1(x),f2k(x)]≥Ld(x,f(x)),∀x∈X

成立，(k为某个正整数)，则f在X中有一不动点。

证明令

+…+d(f2k-1(x),f2k(x))]

于是φ(f(x))-φ(x)

即d(x,f(x))≤φ(f(x))-φ(x),∀x∈X

由于f是连续满射, 从而φ(x)是连续的, 必为下半连续, 由引理3可知,f在X中必有不动点。

三、扩张映射原理的应用

(一)求方程解的存在性

例1[1,6]设f(x,y)在

D:a≤x≤b,-∞

证明在完备空间C[a,b]中作映射T,使对任意的函数φ∈C[a,b], 有

则(Tφ)(x)连续, 即Tφ∈C[a,b]。所以T是C[a,b]到自身的映射, 又对任意的φ∈C[a,b]，有

其中0<θ<1，

按C[a,b]中距离的定义，即知

d(Tφ2,Tφ1)≥αd(φ2,φ1)。

因此，T是扩张映射，由定理1，必有唯一

f(x,φ(x))=0,x∈[a,b]。

(二)求数列极限

解：构造函数

显然f(x)在(0,+∞)上连续可导。

因xn>0，当x>0时，

故xn=f(xn+1)为扩张映射，由定理3知，{xn}收敛。

(三)判定函数不动点

例3[1]设函数

f(x)=x2-1,x∈[1,2]，

显然

f([1,2])=[0,3]⟺[1,2]，

且对任意的x1,x2∈[1,2]的，有

=2d(x1,x2)

例4设函数

f(x)=ex-2,x∈[1,2]，

显然，

f([1,2])=[e-2,e2-2]⟺[1,2]

且f'(x)=ex≥e>1。根据定理2的推论知，f在中[1,2]有不动点。

四、结语

在压缩映射原理的基础上，得到了扩张映射原理及相关的不动点定理，并给出了扩张映射原理的应用实例。通过这些典型的实例可以看出，扩张映射原理的确有很重要的应用。

参考文献：

[1]吴翠兰,王云杰.扩张映射与非压缩映射不动点定理[J].安庆师范学院学报,2010,16(4):17-18.

[2]程其襄,张奠宙,等.实变函数与泛函分析基础[M].北京:高等教育出版社,2003.

[3]张恭庆,林源渠.泛函分析讲义[M].北京:北京大学出版社,2005.

[4]RaviP.Agarawl,MariaMeehan. Fixed Point Theory and Applications[M].Cambridge:CambridgeUniversityPress, 2001.

[5]SehiePark.OnExtensionsoftheFixedPointTheorem[J].Korean Math.Soc, 1983,19(3): 143-151.

[6]杜鸿.压缩映射原理及其应用[J].丽水学院学报,2007,29(2):14-15.

[责任编辑刘江南]

Expansion mapping principle and its application

by LIU Yan-junp.166

In order to improve and develop the fixed point theorem and its application, this paper gives the concept of expansion mapping, proves the principle by using Banach contraction mapping principle, and also gets some other fixed point theorems. Finally, the paper discusses whether the expansion mapping principle can be applied into the fixed point study on the existence of equation solution, seeking the limit of number series, and judging functions.

Keywords:Banach contraction mapping principle; expansion mapping principle; fixed point; existence of solution

中图分类号：O177.91

文献标识码：A

文章编号：1008-6390(2016)02-0166-03

作者简介：柳彦军(1988-)，男，甘肃庄浪人，助教，研究方向: 非线性分析及其应用。

基金项目：重庆市教委科研项目“合作博弈解及其应用研究”(KJ1501407)

收稿日期：2015-10-23