Residual Schemes Applied to an Embedded MethodExpressed on Unstructured Adapted Grids
2016-05-12AbgrallAlcinBeaugendreDobrzynskiNouveau
R. Abgrall, H. Alcin, H. Beaugendre, C. Dobrzynski, L. Nouveau
(1. Universität Zürich, Institut für Mathematik, Winterthurstrasse 190, CH-8057 Zürich, Switzerland 2. University of Bordeaux, IMB UMR 5251, INRIA Bordeaux Sud-Ouest, F-33400 Talence, France 3. INRIA Bordeaux Sud-Ouest, F-33400 Talence, France)
Residual Schemes Applied to an Embedded MethodExpressed on Unstructured Adapted Grids
R. Abgrall1, H. Alcin3, H. Beaugendre2,*, C. Dobrzynski2, L. Nouveau3
(1. Universität Zürich, Institut für Mathematik, Winterthurstrasse 190, CH-8057 Zürich, Switzerland 2. University of Bordeaux, IMB UMR 5251, INRIA Bordeaux Sud-Ouest, F-33400 Talence, France 3. INRIA Bordeaux Sud-Ouest, F-33400 Talence, France)
The interest on embedded boundary methods is increasing in Computational Fluid Dynamics because they simplify the mesh generation problem when dealing with the Navier-Stokes equations. To give a few examples, they simplify the simulation of multi-physics flows, the coupling of fluid-solid interactions in situation of large motions or deformations. Nevertheless an accurate treatment of the wall boundary conditions remains an issue of the method. In this work, a penalty term added to the Navier-Stokes equations accounts for the wall boundary conditions and accuracy is recovered using mesh adaptation, thanks to the potential of unstructured meshes.
Residual schemes, Immersed boundary method, Penalization, Unstructured grids, Mesh adaptation
0 Introduction
When dealing with Computational Fluid Dynamics simulations, two kinds of grids are usually used: body-fitted grids and embedded ones. For body fitted grids, solid wall boundaries are meshed and boundary conditions (BCs) are applied on the wall according to additional equations (Neumann or Dirichlet BCs). On the contrary, immersed boundary methods (IBM) are characterised by a mesh covering the entire domain, and BCs are taken into account in a different way. The penalization technique [1] is an IBM in which the BCs are handled inside the equations by adding source
terms. In this method, the solid body is located on the mesh by the 0 isovalue of the signed distance function. It is then necessary to define this isovalue as well as possible. Mesh adaptation is then introduced [2-4] to catch precisely this isovalue and to accurately compute the penalized source terms. We propose here to solve the penalized compressible Navier-Stokes equations on adapted grids using a residual distri-bution scheme. Those schemes [5-8] are chosen for their easy order increase and parallelization. Penalization combined with mesh adaptation provides a good method to deal with moving bodies. Indeed, for a given (or computed) movement of the
solid body, if the new position and a mesh can be provided, the solution at the new time step can be computed. In this work the penalization technique applied to anisotropic meshes, presented in [1], is extended in the framework of Residual Distribution Schemes (RDS). A methodology is proposed to account for unsteady flows and moving bodies. Again, in order to improve accuracy of the wall treatment we investigate a dynamic tracking of the moving interface. In [4], a methodology is proposed to follow the level-set function by advection and to get dynamic mesh adaptation. In this work, we propose to follow the process proposed in [4] and to track the surface interface with mesh adaptation.
1 Description of the Method
IBM methods are characterized by a mesh covering the entire domain. To take into account solid bodies inside the domain the first step consists in localizing the solids' interfaces (lines in two dimensions and surfaces in three dimensions). A common way for that is to use a level-set function that defines for each node of the mesh the distance between this node and the closest solid interface.
1.1 Signed Distance Function to a Solid
From a practical point of view, the level-set function chosen in this work is the signed distance function (SDF). The SDF is the distance of the considered point to the solid surface with a sign in order to determine if the point is inside or outside the surface. For an inside point, the SDF is negative and for an outside one, the SDF is positive. One way of computing the SDF, see Dapogny and Frey [9], is to solve the unsteady Eikonal equation. The inside of the surface to model is defined by
(1)
withdthe dimension of space andu0a continuous function. Then, the SDF can be considered as the solution of the following unsteady Eikonal equation:
(2)
Using the method of characteristics, the following approached solution is then obtained by the system of Eq. (3):
(3)
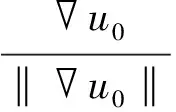

Algorithm1 modifiedalgorithmwithadaptativetimestepforn=1untilconvergencedo un(x)=un-1(x)foreachnodex∈Γ foreachsimplexTofΓdo foreachnodex∈Tnotinitializeddo ifx∉Ωthen dt=minimumheightofT drec=∇un-1‖∇un-1‖dt T2=T whileT2==Tdo ifx∉Ωthen x2=x-drec else x2=x+drec endif FindT2suchthatx2∈T2 ifT2==Tthen drec∗=1.1 endif endwhile ifx∉Ωthen un(x)=min(un(x),un-1(x-drec))+dt else un(x)=min(un(x),un-1(x+drec))-dt endif endif endfor endforendfor
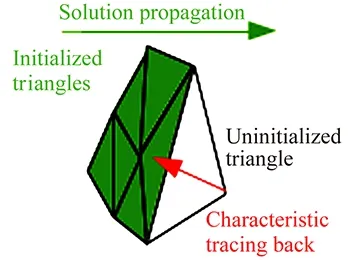
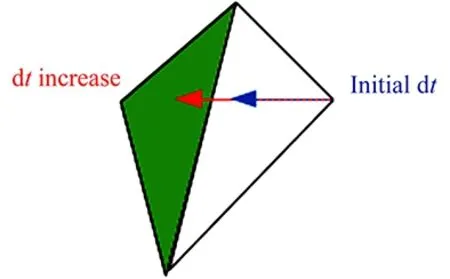
Fig.1 Wanted arrival element while tracing backcharacteristics. Improvement of dt so as to have x∓dt belonging to another element.
Once the SDF is defined over the domain, for each solid bodySithe characteristic function of this solid,χSican be defined such as
(4)
1.2 Penalized Navier-Stokes Equations
When a penalization technique is used as an immersed boundary method the solids around which the flow is computed are defined using the so-called penalization method or Brinckman-Navier-Stokes equations. Here, the solids are considered as porous media with a very small intrinsic permeability. The idea is then to extend the velocity field inside the solid body and to solve the flow equations with a penalization term to enforce rigid motion inside the solid. The sign distance function to the solid is used to capture the interface of the solidSi. The penalty terms are added to the classical Navier-Stokes equations to account for the solids inside the domain, as it is described in Eq. (5). We have
(5)
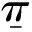
p=(γ-1)ρT
and
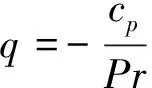
Inthesemodifiedequations,thepenaltytermsaretheterms,whichincludedirectlytheboundaryconditionsofthesolidsintheequations.Indeed,outsidethesolids,theχSifunctionsareequalto0andsothepenalizationtermvanishesandtheusualNavier-Stokesequationsarefoundback.Ontheopposite,insideasolid,thecharacteristicfunctionisequaltoone,andas1/ηis chosen large enough, the penalty terms dominate and the boundary values are imposed. The accuracy of the method depends on the value ofη, in all simulations, we use an implicit scheme withη=1×10-12. This system can be formulated in a matrix way:
∂tU+·F(U)=·G+S
(6)

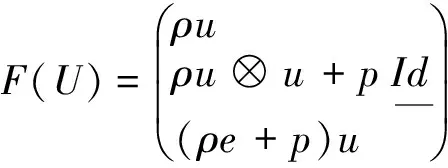

whereUare the conservative variables,FandGare the advection and viscous flux andSthe penalty source term.
1.3 Unstructured Mesh Adaptation
Our numerical simulations are performed on unstructured anisotropic meshes (triangles in two dimensions and tetrahedra in three dimensions). In Abgrall et al.
[1] we propose to combine our level-set based penalization approach to mesh adaptation. The idea is to conserve the simplicity of the embedded approaches for grid generation process and improve the accuracy of wall treatments by using mesh adaptation. Mesh adaptations are performed using two criteria, the signed distance function (interface of the solid body) and the velocity component of the flow solution. As explained in section 1.1, the solid is located on the mesh thanks to the SDF. In order to define as precisely as possible the solid, mesh adaptation with respect to the 0 level set function can be performed. Indeed, it allows refining the mesh close to the solid boundaries. Thus, the penalization is imposed in a rigorous way. In addition, anisotropic meshes are used. Those meshes are defined by the fact that elements (triangles or tetrahedra) can be stretched a lot, which allows inserting fewer elements in refined areas.
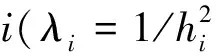
(7)
withR=(φ,v1,v2),where(v1,v2) is a base of the tangential plane of the surface defined by the isovalues ofφ, andλithe eigenvalues of the Hessian ofφ. This metric is imposed in a vicinityWof the surface (see Fig.2).
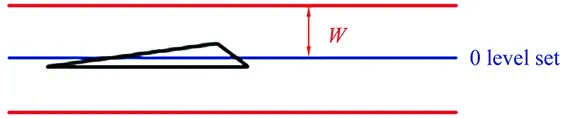
Fig.2 Area of fine mesh integration.
Another important and useful way of using mesh adaptation is in areas of large physical variations. Indeed, it allows refining the mesh in order to better catch some phenomena. Thus, without increasing that much the number of nodes and elements, the solution can be considerably improved. For this kind of adaptation, the aim is to control the interpolation error between the exact solutionuand its interpolant ∏huon the mesh. It has been proved in [3] that an upper bound of this error on an elementKis given by:
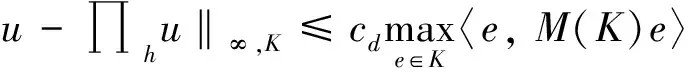
(8)
whereedenote the edges of the mesh,cdis a constant depending on the dimension and the metricM(K) computed with the hessianHuofu:
whereRis the matrix of the eigenvectors of the Hessian , and theλiare defined by:
withhmin(respectivelyhmax) the minimum (respectively maximum) size wanted for the mesh andhithe eigenvalues ofHu. Thus, in area of large physical variations, small elements are inserted, and in area where the solution is quasi constant, large elements are placed.
2 Numerical Schemes
Our numerical simulations are performed on unstructured anisotropic meshes (2D-triangles and 3D-tetrahedra). The system of equations is discretized using residual distribution schemes [8, 10]. Those numerical schemes allow constructing a high order method with compact stencil to ease parallelism.
2.1 Residual Distribution Scheme Construction
The scheme that is used to solve the equations introduced in section 1.2 is a residual distribution scheme (RDS). Here is briefly explained how such schemes are built. More details can be found in [6].
Considering a 2D steady conservation equation:
(9)
AtesselationThofΩis considered. Elements are notedT(boundary ∂T). Letuh=∑iuiφi,φibeingthebasisfunctionschosenonthetriangleT. Eq. (9) integrated overΩcan be written as:
∫Ω·F(uh)dx=0
(10)
WhatiscalledthetotalresidualΦTcan then be defined for each triangle:
ΦT=∫T·F(uh)dx=∫∂TF(uh)·nextds
(11)
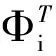
(12)
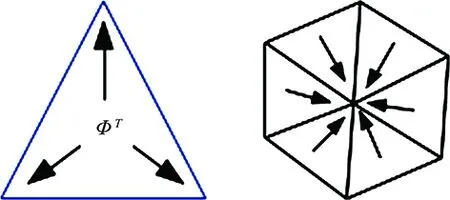
Fig.3 Principle of a residual distribution scheme. Left: distribution for a P1 triangle; Right: gathering all triangles contributions.
The distribution coefficients are defined according to the scheme used (Lax-Wendroff, Lax-Friedrichs, etc…). Then, all the contributions of each triangle whereibelongs to are added (see Fig.3), and the RDS is formulated as:
(13)
The solution of (13) can be obtained by solving the pseudo iterative scheme [5]:
(14)
or more sophisticated iterative methods. An extension to the NS equations is defined in [7] and leads to an Eq. (13), with a total residual taking into account the viscous terms.
A RDS has a consistency property, is a positive scheme and is said linearity preserving.
Consistency: The distribution coefficients must satisfy
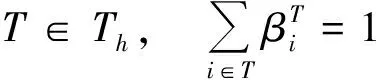
(15)
Nodal Residual Formulation: The nodal residual can be written as
(16)
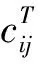
∀i∈Th, ∀Ti,
(17)
PositivitycanbeassimilatedtotheTotalVariationDiminishingprincipleknownforhighorderschemes.Itensuresthatnospuriousoscillationappears.
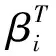
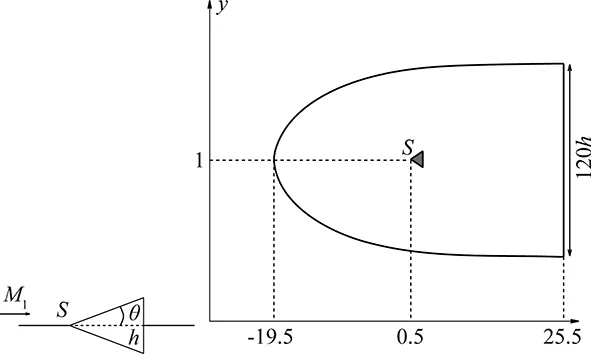
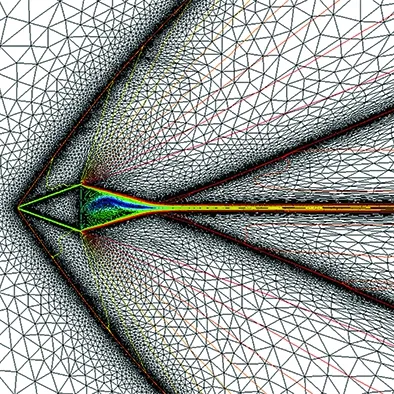
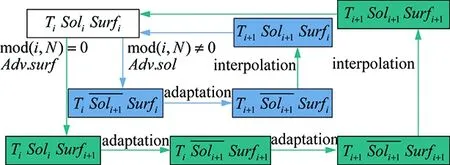
∀i∈Th, ∀iT, || (18) TwoexamplesofRDSaredescribedinthetwonextsections. 2.2 A Variant of the SUPG Scheme or Lax-Wendroff RDS As said before, the RDS depends on the coefficient distribution chosen. The total residual is equally distributed to the DoFs and a stabilization term is added [7]. For P1 triangles, we have (19) Thestabilizationisdefinedsuchthatbothadvectionanddiffusionareconsidered: (20) LookingattheEq. (6),Ais the Jacobian matrix of the advection:A=uFandKis such that:G=KU. 2.3 A Lax-Friedrich Scheme The Jacobian matrixAis decomposed such asA=LΛR,whereΛ=diag(λi)isadiagonalmatrixandR,Lare the matrices of the Eigenvectors. The nodal residual is written as: (21) andthenodalresidualiscomputedasfollows Asforthepreviousscheme,thisschemeiscenteredandneedsastreamlinedissipationterminsmoothregionsoftheflow,theschemeisthengivenby whereτTis defined by Eq. (20), and ∈T(uh)≈1 in smooth regions and 0 close to discontinuities. 2.4 Validations on Numerical Test Cases Using some test cases we demonstrate the ability of the proposed method to obtain an accurate solution along with an accurate wall treatment even when the initial mesh does not contain any point on the level-set 0. 2.4.1 Supersonic Flow Around a Triangle In the first example we consider the supersonic flow around a solid body of triangular shape (heighth=0.5, half angleθ=20°, see Fig.4). The same computational domain as [11] is chosen and the computation is stopped when a steady state is obtained. The Lax-Friedrich RDS scheme is used for this numerical test case. Our initial mesh is only slightly adapted to the 0 level set (see Fig.5(a)). The penalized variables are the velocity (uS=0) and the temperature (TS=3). The Reynolds number is fixed toRe= 50 000 and the Mach number is chosen equal toMa= 2.37 to get a shock in contact with the triangle peak. Fig.4 Studied triangle and domain. (a) Initial mesh (b) Component u of the velocity computed on the initial meshFig.5 Supersonic triangle test case. The componentuof the velocity on the initial mesh is given in Fig.5(b). For the adaptations, the following parameters (for both the level-set and theu-velocity) have been chosen: (22) The mesh obtained after 6 cycles of adaptation and the computedu-velocity on this mesh are presented in Fig.6. A way to validate this test case is to compute the angle between the shock and the horizontal axis because this angle can be analytically computed. As in [1], the angle is measured using a point located on the shock aty=0 and we foundβ=53.33° for a analytic one ofβ≈53.46°. As in Boiron et al. [11] an oblique shock is predicted and attached to the triangle, see Fig.5(b) and Fig.6. Our results are in good agreement with the theory and the numerical solutions performed in [11]. Fig.6 Supersonic triangle, adapted mesh with the component u of the velocity isoline. 2.4.2 Flow Around an Ellipse In this 3D test case taken from [1], the flow around an ellipse (sizes: (0.5,0.1,0.2)) centered in a spherical (radiusr=10) domain is studied. The SUPG like RDS scheme is used for this numerical test. The parameters are set toRe=500 andMa=0.375. As for the previous test case, the initial mesh is only adapted to the 0 level set (see Fig.7(a)). The componentuof the velocity obtained on this mesh is presented in Fig.7(b). Two cycles of adaptation have been done with the following parameters (for both the level-set and theu-velocity adaptation): (23) (a) Initial mesh (b) Corresponding u component of the velocityFig.7 Flow around an ellipse. The adapted mesh is presented in Fig.8(a), and its solution, the componentuof the velocity in Fig.8(b). (a) Adapted mesh (b) Corresponding u component of the velocityFig.8 Flow around an ellipse. 3.1 Unsteady Residual Schemes Now we seek approximations of the solution of a time dependent problem defined by ∂tu+·F(u)=0 (24) FollowingaPetrov-Galerkinfiniteelementapproximationwith weendedupwith,foranydegreeoffreedomi, (25) Letmijbeing the mass matrix coefficient, we define the total flux of Eq. (24) by (26) withΦTdefined by Eq. (11). The discrete counterparts of this equation are then given by (27) We propose to use the idea that in everyT∈Ththecombinationoftermsarisingfromthemultiplicationofthemassmatrixwiththenodaltimederivativesshouldgivebackanintegralofthetimederivativeofuhover a dual sub-elementcj∈T. with|Cj|=βj|T|toguaranteetheconsistency. FollowingthisideathetwostepsoftheexplicitRunge-Kutta2 (RK2)schemearedefinedasfollows (28) Thisconstructionoftheexplicitapproachisbasedonthreemainpoints:firstrecasttheRDdiscretizationasastabilizedGalerkinscheme,thenuseashiftedtimediscretizationinthestabilizationoperator,andlastlyapplyhighordermasslumpingontheGalerkincomponentofthediscretization.Allthedetailsoftheschemeandproofscanbefoundin[10]. 3.1.1SplittingApproach The accuracy of the penalization method depends on the value ofη, in all steady simulations, we use an implicit scheme withη=1×10-12. For unsteady simulations the RK2 scheme described above is an explicit scheme. To overcome CFL restriction due to the penalty source term we propose a splitting algorithm. We solve step 1 and step 2 of Eq. (28) for the classical Navier-Stokes equations, without the penalty source term, then we add a third step to take into account implicitly the penalty source term. (29) 3.1.2NumericalTestonanOscillatingandPitchingAirfoil In this test case, we model an oscillating wing experiencing simultaneous pitchingθ(t) and heavingh(t) motions. The infinitely long wing is based on a NACA 0015 airfoil. The pitching axis is located along the airfoil chord at the position (xp,yp)=(1/3,0).Theairfoilmotionisdefinedbytheheavingh(t) and the pitching angleθ(t) defined as follows (30) whereH0is the heaving amplitude andθ0is the pitching amplitude. The angular frequency is defined byω=2πfand the phase differenceζis set to 90°. The heaving velocity is then given by Vy(t)=H0ωcos(ωt+ζ) (31) Basedontheimposedmotionandontheupstreamflowconditions,theairfoilexperiencesaneffectiveangleofattackα(t) and an effective upstream velocityVeff(t) defined by An operating regime corresponding to the parametersRe=5 000,H0/c=0.5,f=0.14 andθ0=40.1deg has been computed. Fig.9 shows preliminary results for the vorticity at four different times on the fixed unstructured mesh. The motion of the wing is imposed using Eqs. (30) and (31) thanks to the penalty source term. Snapshot of theu-component andv-component of the velocity at timet=2.72 are presented in Fig.10 showing that the penalized components of the velocity are not constant through the wing. (a) t=0 (b) t=1.43 (c) t=1.68 (d) t=2.72Fig.9 Zoom of the NACA 0012 oscillating and pitching airfoil mesh along with vorticity contours. (a) u-component of the velocity (b) v-component of the velocityFig.10 Wind turbine test case, snapshot at time t=2.72. For this test case the interface of the NACA airfoil is moved at each time step and the sign distance function is computed for each new position as described in section 1.1. 3.2 Investigation on Unsteady Mesh Adaptation Further investigations are performed to deal with moving bodies. The first step consists in following the moving body with the adapted grid. Two different approaches can be studied, the first one consists in solving the advection equation which governs the level-set evolution and the second one computes the whole signed distance function on the mesh after each displacement as it has been done in the previous test case. For the first approach, as the body is defined by the sign distance functionφ, for a body moving at speedV(t,x), the SDF is then governed by the following advection equation (32) whereφ0(x) corresponds to the initial position of the object, i.e the initial SDF. Here again the goal is to adapt the mesh to zero isoline of the level-set, and this time at each time step. As studied in [4], a characteristic method can be used. The nodes at timetn+1are considered and their “original position” at timetnis searched by tracing back the characteristic. The mesh is then adapted to this new SDF. As we want to deal with physical displacements, time steps are very small and so are the displacements. Instead of using an iterative process as presented in [4], due to the small movement, the new zero level-set is defined in an already adapted area. Indeed as explained in section 1.3, when adaptation to zero level-set is done, the vicinityWof the zero level-set is also refined. Then, just after the advection, adaptation can be done. A well known problem when dealing with level-set advection is the mass loss. Indeed, each advection leads to a small deformation of the surface. Therefore, another way of thinking is, instead of advecting the whole signed distance function, only the surface defining the solid is advected, and the SDF is computed using the method presented in section 1.1. This is the second approach. With this second approach, no mass loss is introduced. The problem is that computational time for large meshes is considerably higher than with the advective method. Consequently, our idea is to find a way of coupling advection and SDF computation to choose the best compromise between CPU time and quality of the solution. In this work, we combined the simplicity given by the penalization method to compute flow solutions around complex geometries with the power of mesh adaptation to improve accuracy. The accuracy is seek in the localization of the 0 level-set function (to be able to impose correctly boundary conditions inside our IBM) and also in the physical solution (to correctly capture shock waves for example). Another advantage of using IBM is the facility of studying moving bodies. To be able to perform unsteady computations we are studying a way of tracking interfaces on a mesh. The idea is to advect during (N-1) time steps the SDF, and everyNtime steps to advect the surface to compute the whole SDF (see Fig.11). Fig.12 presents the displacement (rotation + translation) of a 3D quadrangle([-0.1,0.1]×[-0.2,0.2]×[-0.05,0.05]) and Fig.13 shows a 2D oscillating and pitching NACA airfoil. The next step will be to couple this unsteady mesh adaptation process to our unsteady penalized residual distribution schemes. Fig.11 Adaptation process, Ti, Soli and Surfidenote respectively mesh, solution and surface at time i. Fig.12 Moving quadrangle, top: isosurface; bottom: mesh cut with level-set. (a) Initial mesh (b) Final meshFig.13 Oscillating NACA airfoil. Acknowledgement: · Experiments presented in this paper were carried out using the PlaFRIM experimental testbed, being developed under the INRIA PlaFRIM development action with support from LABRI and IMB and other entities: Conseil Regional d′Aquitaine, FeDER, Bordeaux University and CNRS (see https://plafrim.bordeaux.inria.fr/). · Computer time for this study was provided by the computing facilities MCIA (Mesocentre de Calcul Intensif Aquitain) Université de Bordeaux et Universitéé de Pau et des Pays de l′Adour. · This study has been carried out in the frame of the investments for the future, Programme IdEx Bordeaux, CPU (ANR-10-IDEX-03-02). · R. Abgrall was supported by part by SNFS grant #200021_153604/1. [1]Abgrall R, Beaugendre H, Dobrzynski C. An immersed boundary method using unstructured anisotropic mesh adaptation combined with level-sets and penalization techniques[J]. JCP,2014, 257: 2014,83-101. [2]Dobrzynski C , Frey P. Anisotropic delaunay mesh adaptation for unsteady simulations[C]//Proceedings of 17th Int. Meshing Roundtable, Pittsburgh, USA, 2008. [3]Frey P, Alauzet F. Anisotropic mesh adaptation for CFD computations[J]. Comput. Methods Appl. Mesh. Engrg., 2005,194:5068-5082. [4]Dapogny C. Bui C, Frey P. An accurate anisotropic adaptation method for solving the level set advection equation[J]. Int. J. Numer. Meth. Fluid, 2011. [5]Abgrall R, Roe P L. High order fluctuation schemes on triangular meshes[J]. J. Sc. Comp., 2003,13: 1-3. [6]Abgrall R. Essentially non-oscillatory residual distribution schemes for hyperbolic problems[J]. J. Comput. Phys., 2006, 214(2): 773-808. [7]Abgrall R, De Santis D. High order residual distribution scheme for Advection-Diffusion problems[J]. Siam J. Sci. Comput., accepted, 2014. [8]Abgrall R, Larat A, Ricchiuto M. Construction of very high order residual distribution schemes for steady inviscid flow problems on hybrid unstructured meshes[J]. JCP, 2011, 230(11):4103-4136. [9]Dapogny C, Frey P. Computation of the signed distance function to a discrete contour on adapted triangulation[J]. Calcolo, 2012, 49:193-219. [10]Ricchiuto M, Abgrall R. Explicit Runge-Kutta residual distribution schemes for time dependent problems: second order case[J]. JCP, 2010, 229(16): 5653-5691. [11]Boiron O, Chiavassa G, Donat R. A high-resolution penalization method for large Mach number flows in the presence of obstacles. Computers and Fluids, 2009,38(3):703-714. 0258-1825(2016)02-0214-10 基于非结构自适应网格和嵌入边界法的残差格式研究 R. Abgrall1, H. Alcin3, H. Beaugendre2,*, C. Dobrzynski2, L. Nouveau3 (1. Universität Zürich, Institut für Mathematik, Winterthurstrasse 190, CH-8057 Zürich, Switzerland; 2. University of Bordeaux, IMB UMR 5251, INRIA Bordeaux Sud-Ouest, F-33400 Talence, France; 3. INRIA Bordeaux Sud-Ouest, F-33400 Talence, France) 嵌入边界法由于在求解NS方程时能够简化网格生成问题而在计算流体领域受到越来越广泛的关注。简言之,嵌入边界法能够简化大变形和运动条件下多物理流动模拟、流固相互作用耦合问题,然而壁面边界条件的精确处理仍旧是该方法需要解决的问题。在本文工作中,为考虑壁面边界条件而在NS方程中增加了补偿项,同时采用非结构网格自适应技术保持了壁面边界条件的精度。 残差格式;浸入边界法;补偿;非结构网格;网格自适应 V211.3 A doi: 10.7638/kqdlxxb-2016.0010 *Assistant Professor, Department of Mathematics; Heloise.beaugendre@math.u-bordeaux1.fr format: Abgrall R, Alcin H, Beaugendre H, et al. Residual schemes applied to an embedded method expressed on unstructured adapted grids[J]. Acta Aerodynamica Sinica, 2016, 34(2): 214-223. 10.7638/kqdlxxb-2016.0010. Abgrall R, Alcin H, Beaugendre H, 等. 基于非结构自适应网格和嵌入边界法的残差格式研究(英文)[J]. 空气动力学学报, 2016, 34(2): 214-223. Received date: 2016-02-04; Revised date:2016-03-27
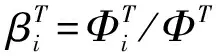







3 Moving Bodies
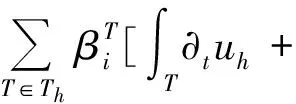
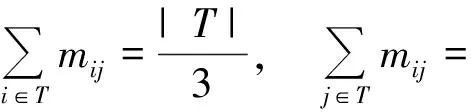
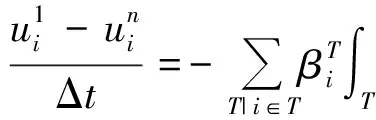
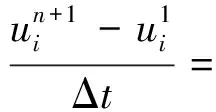
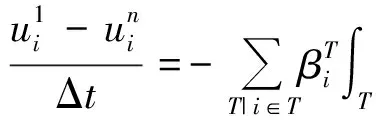
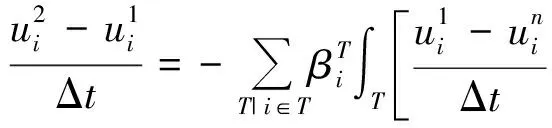
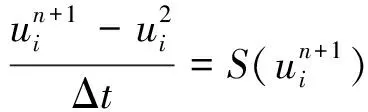
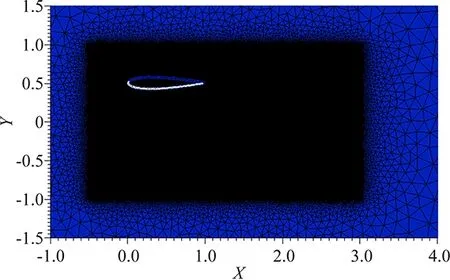
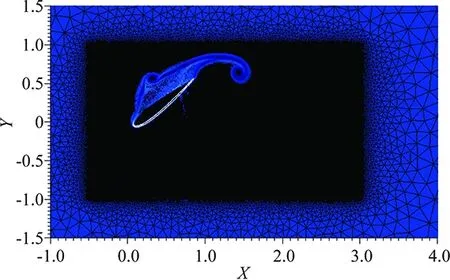
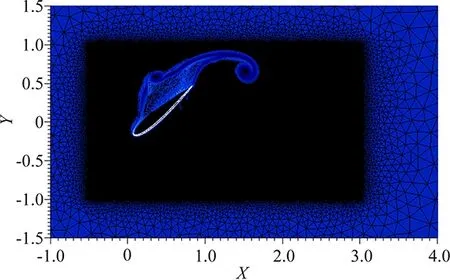
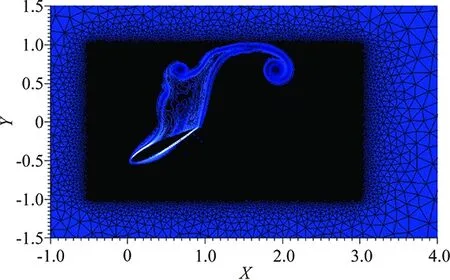

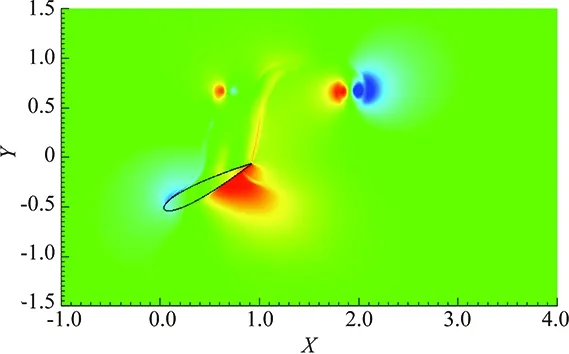
4 Conclusions


猜你喜欢
杂志排行
空气动力学学报的其它文章
- Computational Fluid Dynamicsin Europe, a Personal View
- The History of CFD in China
- Simulations of Transonic Flows withFriction and Heat Addition
- Coupled CFD/RBD Modeling for a BasicFinner Projectile with Control
- High Order Numerical Methods for LESof Turbulent Flows with Shocks
- Vorticity Dynamics and Control of Self-PropelledFlying of a Three-Dimensional Bird
