基于改进PDF技术的间歇过程NFM模型

付钊，贾立（上海大学机电工程与自动化学院自动化系，上海市电站自动化重点实验室，上海 200072）



基于改进PDF技术的间歇过程NFM模型

付钊，贾立
（上海大学机电工程与自动化学院自动化系，上海市电站自动化重点实验室，上海 200072）

摘要：间歇过程是一类具有典型复杂非线性特性的生产过程，可以利用模糊神经网络(NFM)建立其输入输出的非线性映射关系。在前期的研究中曾提出过基于概率密度函数（PDF）技术的模型训练方法，成功解决了传统的基于MSE准则训练方法模型泛化能力弱的问题，但又产生了概率密度难以估计及目标PDF未知时模型性能不稳定的问题。针对这两个问题，引入了新的概率密度窗宽估计方法，并提出了在目标PDF未知时采用PDF预估器及其收缩策略的算法。仿真实验表明：该方法能够保证足够的概率密度估计精度和模型预测性能。

关键词：间歇过程；神经模糊模型；概率密度函数；收缩策略；算法；预测

2015-12-17收到初稿，2015-12-19收到修改稿。

联系人：贾立。第一作者：付钊（1987—），男，硕士研究生。

引 言

间歇过程（batch process）是精细化工、生物制药和食品饮料等生产行业的主要生产方式[1]。由于其机理异常复杂且具有极强的非线性，想要建立其机理模型需要耗费大量的时间与资源[2]。在以信息化为导向的现代工业企业中每天都在产生海量的数据，这些数据在一定程度上隐藏着工业生产的过程信息。如何通过数据模型来有效利用这些离、在线数据为工业生产的优化与控制服务是非常有意义的一个研究课题[3]。

作为数据模型领域的两种代表性的理论方法：模糊理论通过构建模糊集、隶属度函数以及包含专家经验的模糊规则来完成对难以描述的复杂系统的建模；而神经网络则通过其自身强大分布式并行非线性映射能力和学习能力来对系统的非线性进行拟合[4]。而将这两种技术结合所形成的神经模糊系统能够在利用神经网络的自学习与非线性映射能力优糊规则和隶属度函数的同时，利用模糊部分加强神经网络的自控能力以减少人们主观因素的影响，因而具有更为优异的性能[5-7]。

传统的模型训练中往往采用的是以统计指标均方差（MSE）为准则的参数辨识方法。该方法并未考虑输出误差序列的空间分布状态，因而只能算作对理想模型的一种局部逼近，并不能保证所训练出模型的泛化能力。1996年，捷克学者Karny[8]首次提出了概率密度函数（PDF）控制的概念。2007年王宏等[9]针对模型参数在有界区域内随机变化的系统，提出了基于平方根B样条模型的输出PDF跟踪控制策略，并将其成功应用于造纸过程的控制之中。2012年，贾立等[10]在间歇过程的数据驱动建模方法中引入PDF控制的概念，在保证建模精度的同时有效提高了模型的鲁棒性与泛化能力。但是，该方法在应用过程中遇到了两个问题：①概率密度估计的准确度不够高；②当目标PDF信息不能给定时，采用基于最小熵准则进行参数辨识容易出现性能不稳定的情况。能否解决上述问题，直接关系到PDF技术是否能够顺利应用到间歇过程建模之中。为此，本文在前期研究的基础上引入新的概率密度窗宽确定方法。该方法能够自动根据样本分布情况确定窗宽以进行准确的概率密度估计。此外，针对目标PDF信息未知的情况，在构建目标PDF估计器的基础上，采用收缩策略来动态地指导模型的训练过程。

1 基于PDF技术的间歇过程NFM模型

基于PDF技术的模型训练方法将间歇过程数据模型的可调参数作为控制系统的输入，将模型误差的PDF作为控制系统的输出，从而成功地将模型开环辨识问题转化为输出PDF控制问题。通过可调参数控制模型误差的空间分布状态，不仅能够保障模型精度，而且可以控制模型误差的空间分布状态，使建模误差的分布趋近于正态分布，从而避免了采用MSE准则训练模型可能引发的模型误差空间分布不规则的情况[11]。

1.1 NFM模型结构

本文所采用的NFM模型由5层前向网络构成：第1层为模型输入层，共包含ny+nu个节点，且每个输入信号分别对应一个节点，该节点将输入信号传递到下一层；第2层为模糊化层，包括(ny+nu)×N个节点组成（式中N为模糊规则IF-THEN数量），每个节点对应一个隶属度函数，表示一个语言变量值；第3层为模糊条件层，每个节点表示一条模糊规则，计算出每条规则的使用度，由N个节点构成；第4层为模糊决策层，由两个节点组成；最后1层为输出层，由1个节点组成。模型输出可以用式（1）表达

式中，μj(xi)表示高斯型隶属度函数；wj表示第j条模糊规则子集；cji和θj分别为隶属度函数的中心和宽度[12]。此外，为了提高模型精度，模糊规则后件参数可以采用常量形式[式（2）]、线性函数形式[式（3）]或者非线性函数形式[式（4）]来表示。

利用PDF技术对NFM系统的参数wj实现辨识，需要采集模型预测输出序列ˆ { ( )} y k，并结合过程实际输出序列{ ( )}

t y k来获取模型的输出误差序列

t

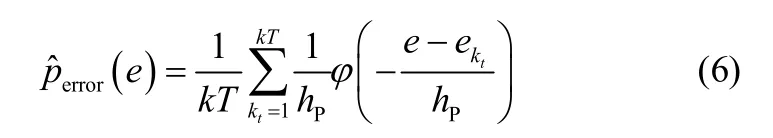
图1 窗宽对概率密度估计的影响Fig.1 Influence of window width on PDF estimation

因此，在实际应用中hP需要根据经验谨慎选择。如在前期研究中，选择的窗宽函数为hP=，其中N为样本序列长度，sig为根据经验选取的窗宽参数（一般取0.25）。然而该窗宽在实际使用中并不能非常好地适应样本分布的变化。为此，采用新的窗宽对样本进行概率密度估计，具体表达式如下

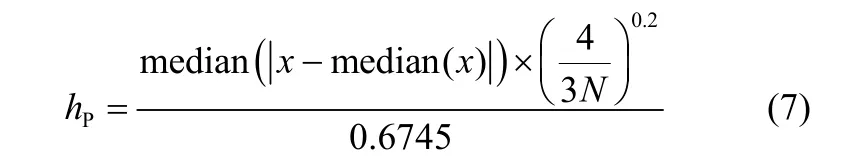
式中，median(x)函数表示序列x的中位数[13]。上述窗宽的选择考虑了样本的分布特性，能够更好地针对样本进行概率密度估计。在获得模型输出误差的PDF之后，就可以通过极小化下述目标函数实现对模型参数wj的求解

通过PDF技术训练出的模型不仅拥有足够高的精度，还可以使建模误差的分布趋近于正态分布，从而避免采用MSE准则可能引发的模型误差空间分布不规则的情况，保证了模型的泛化能力。

1.2 NFM模型参数辨识

间歇过程NFM模型前件参数的作用是根据训练数据来灵活地划分模糊集合，即将间歇过程的非线性模型在空间中分成几个不同的区域以达到减少模糊规则数，增强区域分布合理性的目的。通过改进的最近邻聚类算法对模型的前件参数cji和θj进行辨识[14-15]。对模型后件参数的辨识将采用PDF技术来进行。由于在实际工业生产过程中，目标PDF的信息经常是无法预先获取的，因此在NFM模型后件参数的辨识中就需要分别考虑目标PDF信息能否给定这两种不同的前提条件来设计不同的策略来进行辨识（图2）。

此外，考虑到目标函数式（8）的求解属于复杂的非线性优化问题，而以遗传算法（GA）、模拟退火算法（SA）、粒子群算法（PSO）等为代表的智能优化算法在处理该类问题时能够有效避免传统优化算法易陷入局部最优的问题，且具有较快的收敛速度[16-19]。因此，采用遗传算法对目标函数进行优化求解。

图2 基于PDF技术的间歇过程NFM模型Fig.2 PDF based NFM of batch process

1.2.1 目标PDF已知时NFM后件参数辨识 当目标PDF信息能够被明确给定时，利用PDF技术可以非常方便地通过调节参数wj来实现模型输出误差概率密度函数p(e(kt))对目标ptarget的跟踪。考虑到概率密度函数的图形特性，对目标ptarget和模型输出误差p(e(kt))这两个概率密度函数的差值绝对值进行积分，即通过最小化下述目标函数来调节模型的参数，使两条概率密度曲线之间的差异最小化。

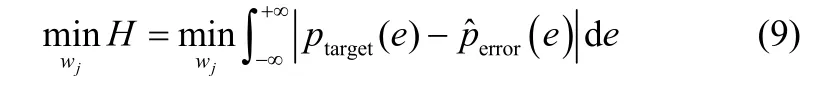
算法的具体操作步骤如下。

（1）采集间歇过程K个批次上的输入输出数据，并将这些数据在时间轴上展开，作为训练的样本数据；

（2）确定核估计的窗函数ϕ，窗宽hP及目标ptarget；

（3）采用聚类算法计算前件参数cji和θj，随机初始化NFM后件参数wj并计算模型的预测输出；

（5）将模型输出误差PDF代入目标函数式（9）中，使用遗传算法通过调节wj值来极小化目标函数。

1.2.2 目标PDF未知时NFM后件参数辨识 考虑到在实际生产过程中经常会存在目标概率密度函数信息未知的情况，在前期的研究中曾提出了一种基于最小熵的模型参数辨识方法。该方法采用信息熵来度量模型误差分布的不确定性，并通过最小化模型输出误差序列的熵值来调节模型参数。如果用p(e(kt))表示模型误差的概率密度函数，则相应的熵值可以表示为

依此可建立下述目标函数的表达式以指导NFM后件参数的调整

由于基于最小熵的PDF技术在应用中存在性能不稳定的缺点，本节拟采用线性ARX模型来搭建一个简易的PDF预估器，然后通过应用PDF收缩策略来求解模型参数。利用间歇过程数据所建立的ARX模型可以表示如下

相应的模型输出误差序列为

式中，yi表示间歇过程实际输出，表示ARX模型输出。利用该误差序列ek, i估计出NFM模型的一个概略目标PDF（该PDF估计值仅使用标准差σ信息，均值μ取为0）

由于间歇过程具有很强的非线性，利用其生产数据所建立的线性ARX模型在估计性能上相对于训练好的非线性NFM模型更弱一些，具体表现为在模型输出误差带上前者的分布表现得更为离散（图3），且概率密度曲线更加矮、宽（图4）[20]。

因此，可以考虑在所建立的ARX预估值基础之上再设定一个PDF收缩策略指导算法更新所跟踪的目标PDF值

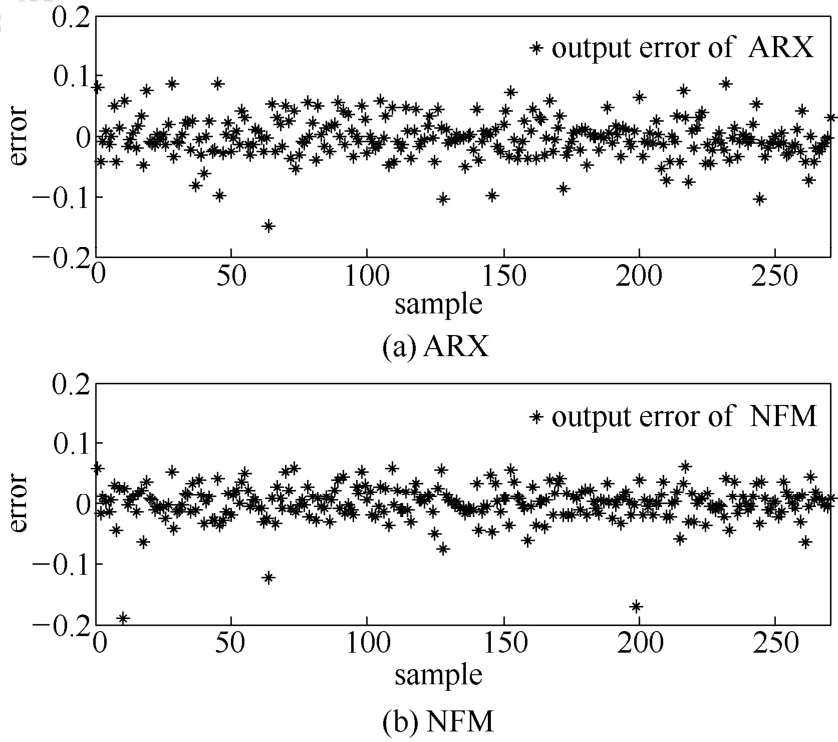
图3 ARX和NFM模型输出误差带示意图Fig.3 Output error band of ARX and NFM

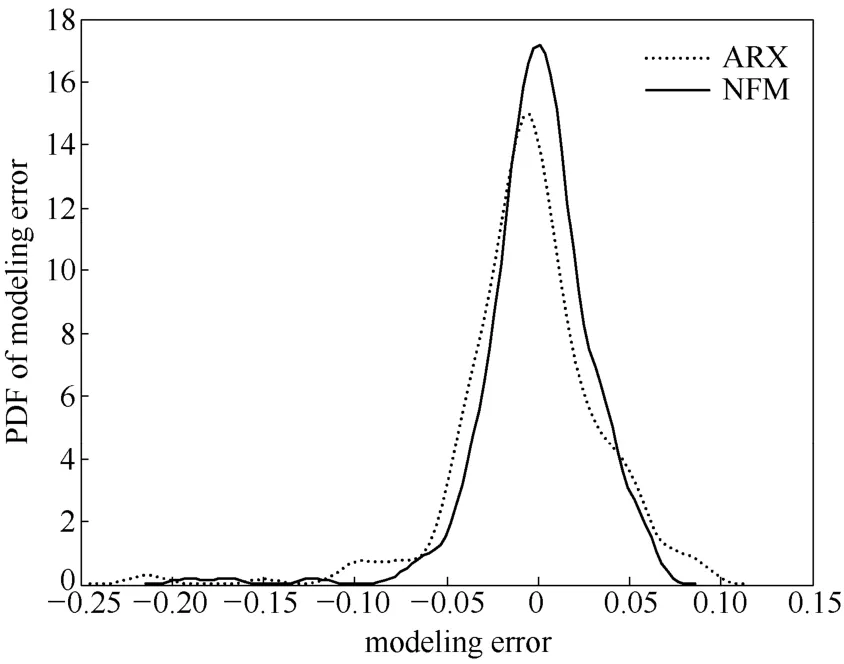
图4 ARX和NFM模型输出误差PDFFig.4 Output error PDF of ARX and NFM

因此，可以考虑设定下述收缩策略的停止条件对收缩过程进行限定

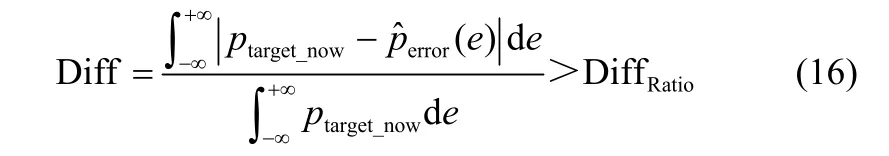
式中，Diff为跟踪偏移率；DiffRatio为预先设置的收缩策略终止阈值（需要根据实际情况设定）。如果模型的跟踪偏移率大于DiffRatio，则判定该算法达到性能极限从而停止PDF收缩并跳出优化进程，输出所保存的上一轮优化的结果。目标PDF的收缩过程大致可以用图5表示，图中高度最低PDF曲线为PDF预估器获得的初始目标PDF；中间层的PDF曲线为应用收缩策略时的目标PDF；高度最高的曲线为达到停止条件时的目标PDF。图中曲线高度由低变高的过程则表示收缩策略的运行情况。

图5 目标PDF收缩效果Fig.5 Contraction of target PDF

（1）采集间歇过程K个批次上的输入输出数据，并将这些数据在时间轴上展开，作为训练的样本数据；

（2）确定核估计的窗函数ϕ，窗宽hP；

（3）利用ARX预估器获取初始目标PDF；

（4）采用聚类算法获取前件参数cji和θj，随机初始化NFM后件参数wj并计算模型的预测输出；

（6）将模型输出误差PDF代入目标函数式（9）中，使用遗传算法通过调节wj值极小化目标函数；

（7）判断是否达到收缩策略终止条件。若未达到终止条件，则应用收缩策略更新目标PDF并将当前最优wj作为初始值重新开始优化；若达到终止条件，则输出系统所保存的上一次优化结果最优值及对应的目标PDF作为最终优化结果。

2 仿真研究

为验证本文提出的算法的有效性，仿真中采用一种典型的间歇生产过程反应器[21]。其反应过程为，表达式为

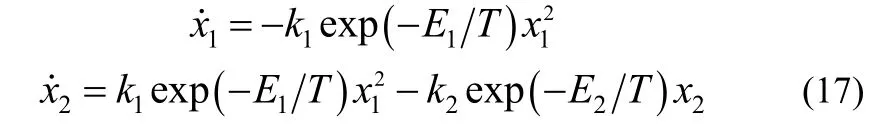
式中，x1和x2分别表示A和B的量纲1浓度；T为反应器温度。仿真中取同时对T进行归一化处理其中Tmin和Tmax分别为298 K和398 K，tf= 1.0 h。

称取5.0 g的刺葡萄皮各3份，加入0.4%盐酸溶液100 mL，于恒温40℃下水浴浸提40 min后过滤。滤渣在相同浸提条件下再进行多次浸提。确定完全浸提花青素所需次数。

取初始条件为：x1(0) = 1，x2(0) = 0。Td为控制变量，且0≤Td≤1，x2( t )为输出变量，控制优化的性能指标是要最大化B的批次终点浓度x2( tf)。

2.1 基于改进窗宽PDF技术性能仿真

为验证提出的改进窗宽估计对基于PDF技术的NFM模型的跟踪性能的影响，仿真中将目标PDF的标准差分别选定为0.030、0.025和0.020。然后利用原始窗宽和改进窗宽对分别进行估计，并利用PDF技术来训练NFM。在上述3种目标PDF下，模型的跟踪效果如图6～图11所示。通过对比可发现，在使用改进窗宽之后，基于PDF技术的NFM系统对目标PDF的跟踪性能得到了很大提升。在其跟踪性能范围之内能够使模型输出误差的PDF对目标PDF实现非常精准的跟踪，进而说明了在PDF技术中引入改进窗宽的有效性与必要性。

图6 目标PDF为0.03时原始估计跟踪效果Fig.6 Original tracking effect of target PDF (0.03)

图7 目标PDF为0.03时改进估计跟踪效果Fig.7 Improved tracking effect of target PDF (0.03)

2.2 目标PDF已知时NFM模型辨识仿真

在本例仿真实验中，已知间歇过程输出误差序列的目标PDF值为。首先根据经验选定模糊空间划分数为8，并使用改进最近邻聚类算法对前件参数cji和θj进行辨识；然后在获得前件参数之后利用改进窗宽估计的PDF技术对后件参数wj进行辨识与优化。

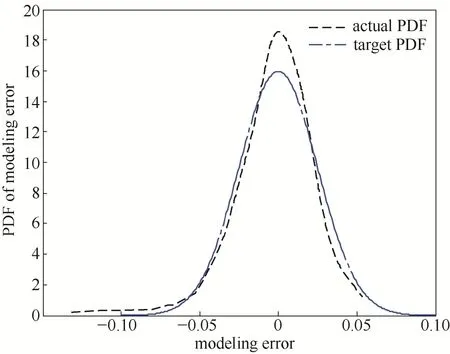
图8 目标PDF为0.025时原始估计跟踪效果Fig.8 Original tracking effect of target PDF (0.025)

图9 目标PDF为0.025时改进估计跟踪效果Fig.9 Improved tracking effect of target PDF (0.025)

图10 目标PDF为0.02时原始估计跟踪效果Fig.10 Original tracking effect of target PDF (0.02)

通过仿真，可知模型训练的输出误差MSE= 6.79×10−4，模型测试的输出误差MSE= 7.49×10−4；此外，模型的训练与测试的输出效果如图12～图17所示，从图中可以看到，经过训练后的模型输出误差PDF能够非常好地跟踪目标PDF，而且当其进行测试输出时其输出误差PDF曲线也趋近于高斯分布。

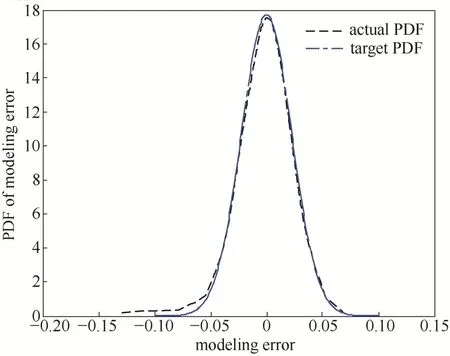
图11 目标PDF为0.02时改进估计跟踪效果Fig.11 Improved tracking effect of target PDF (0.02)

图12 模型的训练输出Fig.12 Output of model training

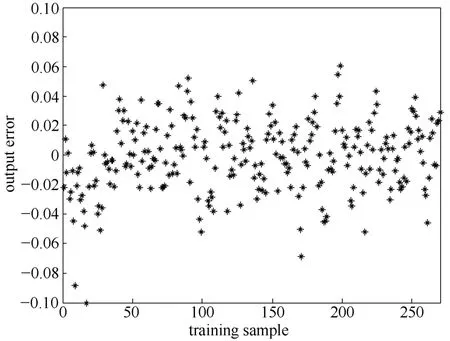
图13 模型的训练输出误差Fig.13 Output error of model training

2.3 目标PDF未知时NFM模型辨识仿真

在目标PDF信息未知时，同样可以首先通过改进最近邻聚类算法对前件参数进行辨识；然后利用PDF预估器来获取初始目标PDF值；最后，采用PDF收缩策略来构建优化算法对NFM后件参数进行辨识。

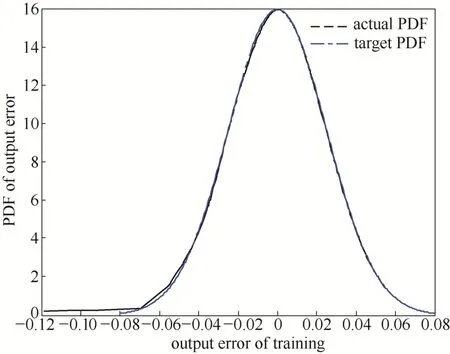
图14 模型的训练输出误差PDFFig.14 Output error PDF of model training

图15 模型的测试输出Fig.15 Output of model testing

图16 模型的测试输出误差Fig.16 Output error of model testing

本次仿真中，PDF收缩策略的收缩系数β=0.9，跟踪偏移率阈值选为DiffRatio= 0.05，即PDF收缩策略为

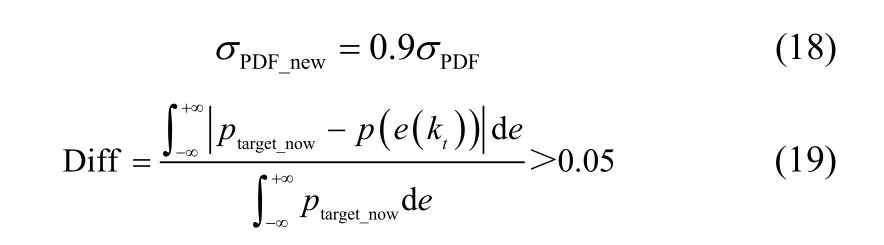
图17 模型的测试输出误差PDFFig.17 Output error PDF of model testing

图18 模型训练时目标PDF收缩示意图Fig.18 Contraction of target PDF in model training

图19 模型的训练输出Fig.19 Output of model training

仿真结果如图18～图26所示，其中图18为PDF收缩策略的运行结果，图中高度最低的一条曲线为ARX预估器所估计的目标PDF，最高的一条曲线为满足PDF收缩策略终止条件时的目标PDF。

图20 模型的训练输出误差Fig.20 Output error of model training

图21 模型的训练输出误差PDFFig.21 Output error PDF of model training

图22 模型的测试输出Fig.22 Output of model testing

基于收缩策略的PDF技术的NFM模型训练输出误差MSE= 6.63×10−4，测试输出误差MSE= 8.40×10−4；而采用最小熵方法求解出的模型训练输出误差MSE= 6.84×10−4，测试输出误差MSE=9.76×10−4。两种算法在MSE指标上并没有太大差异，但是从图21和图25以及图24和图26可以明显看出，基于收缩策略的PDF技术所训练出的模型，无论是训练输出误差PDF曲线还是测试输出误差PDF曲线均更趋近于高斯分布，因此该模型具有更强的泛化能力。

图23 模型的测试输出误差Fig.23 Output error of model testing

图24 模型的测试输出误差PDFFig.24 Output error PDF of model testing

图25 基于最小熵的模型训练误差PDFFig.25 Output error PDF of minimum entropy based model training

图26 基于最小熵的模型测试误差PDF图Fig.26 Output error PDF of minimum entropy based model testing

3 结 论

针对PDF技术在间歇过程NFM模型应用中的不足之处提出了改进方法。在概率密度估计方法中引入全新的窗宽计算方法，从而在实现更为精准的概率密度估计的同时使NFM的训练过程能够更为精确地跟踪目标PDF。此外，针对目标PDF未知的情况引入了PDF预估器和收缩策略来实现模型参数的辨识与优化，提高了模型的预测性能与泛化能力。通过上述改进，使PDF技术在NFM模型中的应用更加成熟与稳定，因而可以很方便地扩展到其他模型中进行应用。

References

[1] 陆宁云, 王福利, 高福荣, 等. 间歇过程的统计建模与在线监测[J]. 自动化学报, 2006, 32 (3): 400-410.

LU N Y, WANG F L, GAO F R, et al. Statistical modeling and online monitoring for batch processes [J]. Acta Automatic Sinica, 2006, 32 (3): 400-410.

[2] 杨志才.化工生产过程中的间歇过程——原理、工艺及设备[M]. 北京: 化学工业出版社, 2001: 5-12.

YANG Z C. Batch Process in Chemical Engineering— Principle, Technology and Equipment [M]. Beijing: Chemical Industry Press, 2001: 5-12.

[3] 侯忠生. 数据驱动控制理论及方法的回顾和展望 [J]. 自动化学报, 2009, 35 (6): 651-654.

HOU Z S. On data-driven control theory: the state of the art and perspective [J]. Acta Automatic Sinica, 2009, 35 (6): 651-654.

[4] 丛爽. 神经网络、模糊系统及其在运动控制中的应用 [M]. 合肥:中国科学技术大学出版社, 2001: 30-42.

CONG S. Neural Network, Fuzzy System and Its Application in Motion Control [M]. Hefei: University of Science & Technology China Press, 2001: 30-42

[5] HAYASHI Y, NAKAI M. Automated exaction of fuzzy IF-THEN rules using neural networks [J]. Transactions of the Institute of Electric Engineers of Japan, 1990, 110 (3): 198-206.

[6] YU Z, LI S, DU H. Adaptive neural output feedback control for stochastic nonlinear systems with unknown control directions [J]. Neural Computing & Applications, 2014, 25 (7/8): 1979-1992.

[7] 丛爽. 几种模糊神经网络系统关系的对比研究 [J]. 信息与控制, 2001, (6): 486-491.

CONG S. Comparative research on relationships between several fuzzy-neural network systems [J]. Information and Control, 2001, (6): 486-491.

[8] Karny M. Toward fully probabilistic control design [J]. Automatica, 1996, (32): 1719-1722.

[9] 陈海永, 王宏. 基于LMI的参数随机变化系统的概率密度函数控制 [J]. 自动化学报, 2007, (11): 1216-1219.

CHEN H Y, WANG H. PDF control of stochastic parameter system using linear matrix inequalities [J]. Acta Automatica Sinica, 2007, (11): 1216-1219.

[10] 贾立, 曹鲁明, 邱铭森. 基于建模误差PDF形状的间歇过程数据驱动模型 [J]. 仪器仪表学报, 2012, (7): 1505-1512.

JIA L, CAO L M, CHIU M S. Modeling error PDF shape based data-driven model for batch processes [J]. Chinese Journal of Scientific Instrument, 2012, (7): 1505-1512.

[11] DING J L, CHAI T Y. Offline modeling for product quality prediction of mineral processing using modeling error PDF shaping and entropy minimization [J]. IEEE Transactions on Neural Networks, 2011, 22 (3): 408-419.

[12] JIA L, CHIU M S. Research on fuzzy neural model with global convergence for batch process [J]. Information and Control, 2009, 38 (6): 683-691.

[13] BOWMAN A W, AZZALINI A. Applied Smoothing Techniques for Data Analysis [M]. New York: Oxford University Press, 1997.

[14] 贾立. 神经模糊系统研究及其在建模与控制中的应用 [D]. 上海:华东理工大学, 2002: 10-32.

JIA L. Research on neuro-fuzzy system and its application in modeling and control [D]. Shanghai: East China University of Science and Technology, 2002: 10-32.

[15] 贾立, 程大帅, 曹鲁明, 等. 基于数据的间歇过程时变神经模糊模型研究 [J]. 计算机与应用化学, 2011, 28 (7): 915-918.

JIA L, CHENG D S, CAO L M, et al. Research on data-based time-varying neuro-fuzzy model for batch processes [J].Computers and Applied Chemistry, 2011, 28 (7): 915-918.

[16] 王建平, 胡益, 侍洪波. 基于高阶偏最小二乘的间歇过程建模 [J].化工学报, 2014, 65 (9): 3527-3534.

WANG J P, HU Y, SHI H B. Modeling of batch process based on higher order partial least squares [J]. CIESC Journal, 2014, 65 (9): 3527-3534.

[17] 史洪岩, 苑明哲, 王天然, 等. 间歇过程动态优化方法综述 [J].信息与控制, 2012, (1): 75-82.

SHI H Y, YUANG M Z, WANG T R, et al. A survey on dynamic optimization methods of batch processes [J]. Information and Control, 2012, (1): 75-82.

[18] 朱朝艳, 王建波, 王学志, 等. 改进遗传算法的研究现状分析 [J].吉林水利, 2010, (7): 1-4.

ZHU C Y, WANG J B, WANG X Z, et al. The status quo of improved genetic algorithm [J]. Jilin Water Resources, 2010, (7): 1-4.

[19] 王梦寒, 杨海, 李雁召. 前馈神经网络与遗传算法相结合解决曲轴中心缩孔 [J]. 化工学报, 2013, 64 (10): 3673-3678.

WANG M H, YANG H, LI Y Z. Elimination of voids in crankshaft through a hybrid of back propagation neural network and genetic algorithm [J]. CIESC Journal, 2013, 64 (10): 3673-3678.

[20] 张炤, 张素, 章琛曦, 等. 基于支持向量机的概率密度估计方法[J]. 系统仿真学报. 2005, 10: 2355-2357.

ZHANG Z, ZHANG S, ZHANG C X, et al. Density estimation based on support vector machines [J]. Journal of System Simulation. 2005, 10: 2355-2357.

[21] XIONG Z H, ZHANG J, WANG X, XU Y M. Run-to-run iterative optimization control of batch processes based on recurrent neural network [J]. Advances in Neural Networks, 2004, 3174: 97-103.

研究论文

Received date: 2015-12-17.

Foundation item: supported by the National Natural Science Foundation of China (61374044), the Shanghai Science Technology Commission (12510709400), the Shanghai Municipal Education Commission (14ZZ088) and the Shanghai Talent Development Plan 2013.

Improved PDF technology based NFM for batch process

FU Zhao, JIA Li
(Shanghai Key Laboratory of Power Station Automation Technology, Department of Automation, School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 200072, China)

Abstract:Batch process is an typical nolinear production process and can be simulated by a neuro-fuzzy model (NFM). In the previous research, a new model training method called PDF technology was proposed to successfully conquer the weak generalization ability which caused by the MSE rule based model training. But the density function is hard to estimate and the trained model are not stable when the target PDF can not given. To solve these problems, a new window width estimation method is introduced and also a contraction strategy with a PDF predictor is proposed when the target can not be given. Simulation results demonstrate that the proposed methods can get a more accurate density estimation and a more excellent model prediction ability.

Key words:batch process; neuro-fuzzy model; probability density function; contraction strategy; algorithm; prediction

DOI：10.11949/j.issn.0438-1157.20151922

中图分类号：TP 273

文献标志码：A

文章编号：0438—1157（2016）03—0998—10

基金项目：国家自然科学基金项目（61374044）；上海市科委国际合作项目（12510709400)；上海市教委创新重点项目（14ZZ088）；2013年度上海市人才发展基金项目。

Corresponding author:Prof. JIA Li, jiali@staff.shu.edu.cn