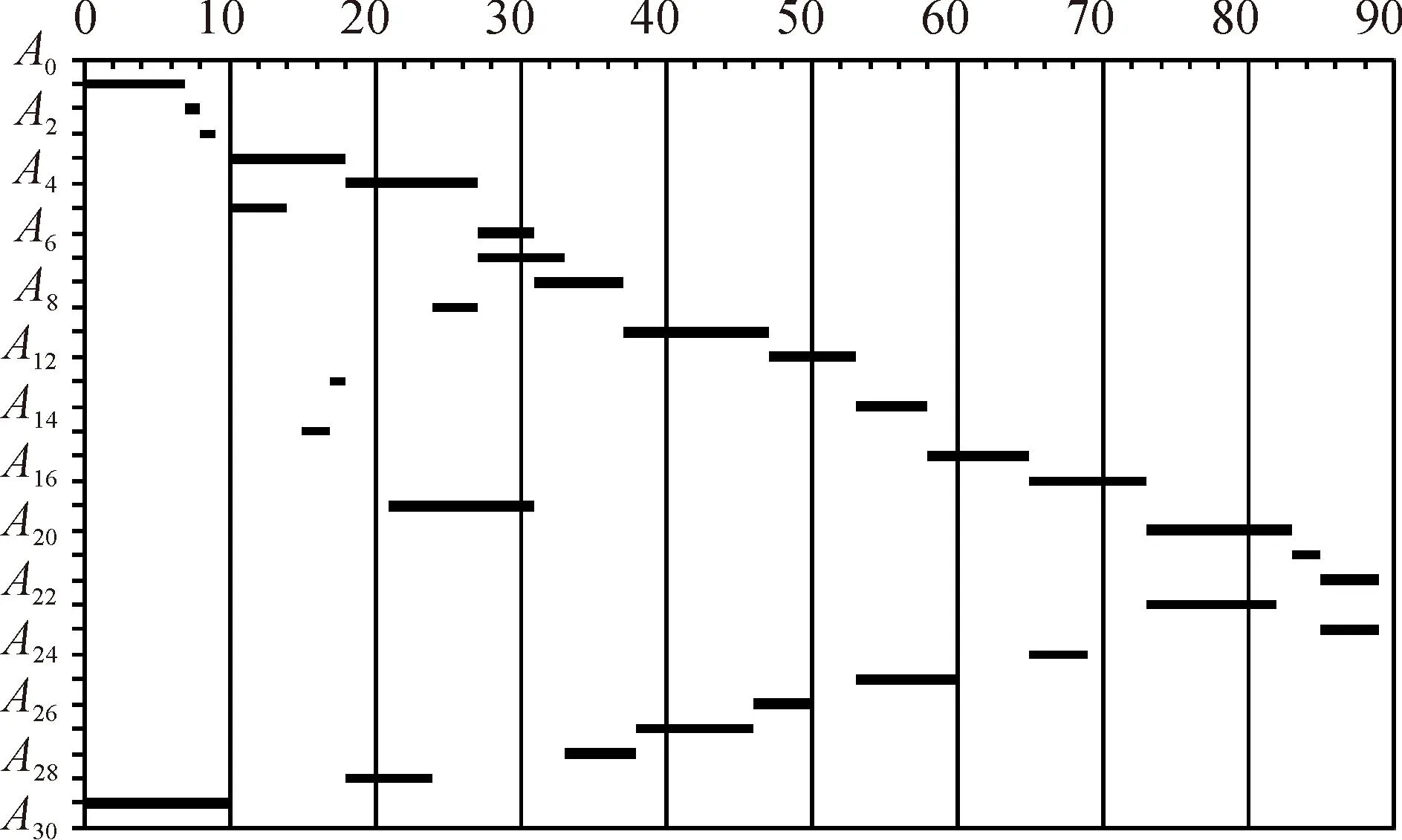
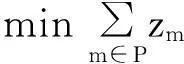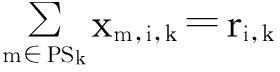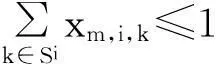基于均衡优化的项目多技能人力资源指派与调度方法

李　明, 徐　哲

(1. 石家庄铁道大学 经济管理学院，石家庄 河北 050043；2. 北京航空航天大学 经济管理学院，北京 100191)



基于均衡优化的项目多技能人力资源指派与调度方法

李明1,2, 徐哲2

(1. 石家庄铁道大学 经济管理学院，石家庄 河北 050043；2. 北京航空航天大学 经济管理学院，北京 100191)

摘要：为提高项目人力资源使用效率，提出一种项目多技能人力资源调度与指派优化方法。首先，采用启发式方法对项目进行资源均衡优化，降低人力资源需求高峰用量；然后，识别调度方案中活动间的重叠关系并将其转化为人员指派优化问题的有效约束；最后，建立整数规划模型并通过编程计算。研究结果表明，使用该方法可快速地找到问题的近优解，用较少的人力资源完成项目任务，从而有效地降低项目人力资源成本。

关键词：人力资源； 均衡优化； 多技能； 项目调度； 指派

对于软件开发、产品研发、项目咨询等以智力和技能劳动为主的项目导向型企业，具有明显技能特征的人无疑是其核心和关键资源。研究表明，使用多技能策略能够减少人员在项目上频繁流动，延长人员在项目上的平均工作时间，从而有助于降低项目成本提高效益[1]。实践中，管理者大都凭借个人经验和直觉对多技能人员进行调度和指派，难以保证项目人力资源使用的合理性[2]。

项目多技能人员调度和指派涉及两方面的问题：项目活动时间调度和多技能人员指派。资源受限项目调度(resource-constrained project scheduling problem，RCPSP)是项目管理研究领域的经典问题，它要求在满足项目活动优先关系和资源约束的前提下，合理安排项目的进度计划，从而优化项目的调度目标[3]。现有文献中，RCPSP问题的优化目标涉及项目工期[4]、资源总成本[5]、资源均衡[6]、项目净现值[7]等诸多方面。在人力资源为单技能同质的情况下，该问题退化为一般的RCPSP问题，但是，当人力资源具有多技能时，虽然理论上可按多模式项目调度问题(multi-mode RCPSP)求解，但是，Bellenguez和Néron[8]指出，由于每个活动的资源分配模式数量太大，采用MM-RCPSP建模求解并不可行。Heimerl和Kolisch[9]指出同时求解活动时间调度和员工指派是一个NP难问题。现有文献中关于项目人力资源调度和指派问题的研究并无统一框架。Heimerl和Kolisch[9]等研究多IT项目多技能人员指派问题，建立了混合整数规划(MIP)模型，优化目标为内外部人力资源总成本最低。但是，在该研究中未考虑项目活动时间调度问题。Alfares和Bailey[10]研究施工项目人员安排问题，用最小用工成本在最短的工期内完成项目，但在该研究中假设人员为单技能且效率同质。Wu和Sun[11]针对多项目调度和人员指派问题建立数学模型，人员效率异质并且具有学习效应，优化目标为外包成本最低。该研究虽在概念模型中考虑了学习效应，但其所使用的遗传算法却未能体现学习效应。Attia等[12]提出具有柔性活动时间、人员技能多样且存在学习与反学习效应情况下的多阶段项目人员指派模型，用来进行多阶段项目规划决策。Isabel和Francisco[13]假设多技能人力资源成本包括固定成本和变动成本且每个项目活动需要多种技能，同时最小化人力资源总成本和项目工期。卢鹏宇等[14]针对多IT项目人力资源调度问题，将项目的演进时间划分为相等的时间片段，建立人员调度方案搜索树，以方案的提前完工率为指标寻找最优解。Li和Womer[15]提出一种Benders分解算法，求解人力资源受限项目调度问题，目标为总人力资源成本最低，但在该研究中，假设各活动对所需技能的需求数量均为1，从而限定了人力资源的指派规模。

通过对文献梳理发现，仅有少数研究[8,15-16]同时考虑项目活动时间调度和人员指派问题，而且优化大多考虑成本目标。虽然成本可在一定程度上反映方案的最优性，但是，当技能人员使用固定工资制时，以活动时间为基础的成本优化目标就会变得不再可行。因此，直接研究资源本身的使用效率可能更有意义。基于此考虑，本文以人力资源使用数量最少为优化目标，对项目多技能人力资源调度与指派问题展开研究：首先进行资源均衡优化调度，使项目对人力资源使用需求高峰用量尽可能降低；然后在调度方案确定的情况下，分析活动之间的重叠关系并将其转换为人员指派约束，之后，建立整数规划模型并采用CPLEX编程求解。

1问题建模

1.1模型问题与假设条件

考虑项目管理中实际场景：一方面，项目中每项活动需要多种技能且每种技能有一定的数量需求；另一方面，企业存在一个人力资源池，其中每个人员均掌握多种技能。问题是，如何对项目活动时间进行调度，同时对人员进行指派，在保证项目按期完成的情况下，所用人力资源数量最少。

本问题建模采用下列假设条件：

1)活动任务不能中断，一旦活动开始，就会持续进行，直至全部完成。

2)活动资源率固定不变，即在活动持续期间，其所需的各种技能人员数量保持不变。

3)同时技能要求，即一个任务所需的各种技能必须同时进行。

4)单一技能使用要求，即一个人员在任一时间，只能在一个活动上使用一种技能。

5)活动的持续时间保持不变，活动之间的逻辑关系亦不允许改变。

1.2符号含义

1)项目活动数据。

G=(A,E,d)，其中：A={A1,A2,…AN}表示项目活动集合，A1是开始节点虚工作，AN是结束节点虚工作，总共有N个活动，i=1,…N,j=1,…N表示活动索引；di表示活动Ai的作业持续时间；E表示活动关系集合，如果存在(Ai,Aj)∈E，则Ai是Aj的紧前活动。

ESi、EFi、LSi和LFi分别表示活动Ai的最早开始时间、最早完成时间、最迟开始时间和最迟完成时间；T表示项目的计划工期。

2)人力资源技能参数。

3)决策变量。

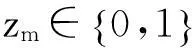
1.3数学模型

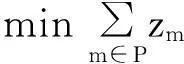
(1)

s.t.

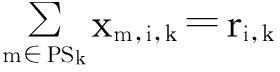
(2)

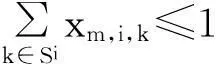
(3)

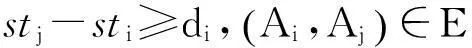
(4)

sti+di≤T,∀Ai∈A；

(5)

xm,i,k+xm,j,k′≤yi,j+yj,i+1,∀Ai∈A,Aj∈A,k∈K,k′∈K,∀pm∈P；

(6)

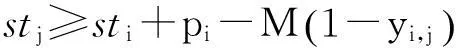
(7)

式(1)为目标函数，即最小化使用的人力资源数量；式(2)表示安排至活动Ai使用技能sk的人数恰好等于该活动对技能sk需求的人数ri,k；式(3)保证任一个人在同一个活动上所使用的技能不超过1项；式(4)表示需满足活动间的紧前约束关系；式(5)表明对任一活动，其完成时间应不超过计划工期；式(6)表示，如果活动Ai和Aj被安排给同一个人，那么这两个活动时间不能重叠；式(7)用来保证变量yi,j取值与活动时间约束的一致性：如果Ai在Aj之前完成，yi,j=1，此时，约束变为stj≥sti+pi，如果在Aj开始之前，Ai尚未完成，yi,j=0，此时，约束变为stj≥sti+pi-M，约束条件恒成立。

该问题的求解与两个子问题有关：1)项目活动时间调度问题，活动时间调度决定整个项目的人力资源需求曲线，该曲线的峰值构成相应调度方案人员需求用量的下界；2)人员指派问题，同一调度方案下，不同指派方案所需人员数量不同。本文求解的基本思路是先对项目所需各种技能人员的总量采用启发式方法进行均衡优化，尽可能降低资源需求曲线最高峰的值，然后以均衡优化后的调度方案为基础，求解人员指派问题，最终得到问题的近优解。

2资源均衡优化启发式方法

资源均衡优化是指在保证项目工期不变的情况下，通过对非关键活动时间的调整，使项目对资源需求的变动尽可能小。文献中资源均衡优化方法主要有两类：1)精确算法，主要包括整数规划、分支定界和动态规划等，但这些方法只适用于小规模问题，无法用于实际工作中大规模问题的计算[6]；2)启发式方法，包括最小矩法[17]、改良最小矩法[18]和遗传算法[19]等。启发式方法简单易懂，虽然只能获得问题近优解，却是解决实际大规模问题的主要方法。

本文首先以项目对各类技能人力资源总需求的最高峰用量最低为优化目标，构建启发式方法进行均衡优化，具体过程如下。

2.1确定基础资源直方图

按照活动总时差与活动持续时间的关系，可将活动分成3类。

Ⅰ类活动，即总时差为零的关键活动，Ⅰ类活动在不影响总工期的情况下不拥有任何机动时间，在整个项目时间表中的位置固定不变。如图1中活动A，它在整个项目实施期间只有一种位置方案，即开始时间为10，完成时间为20，在此期间该活动所需的人力资源数量保持不变。

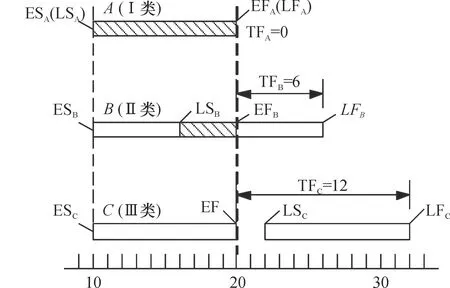
图1　三类活动示意图

Ⅱ类活动，指总时差小于活动持续时间的非关键活动，Ⅱ类活动的时间范围可分成两部分：必须占用时段和可能占有时段。如图1中活动B，其持续时间为10 d，总时差为6 d，可能的开始位置方案总共有TFB+1=7种，分别为10、11、12、13、14、15、16。但是，无论采用何种位置方案，LSB～EFB(图中斜线阴影部分)都为活动B必须占用的时段，在该区间活动对资源的需求不会随位置方案的改变而改变。

Ⅲ类活动，指总时差大于等于活动持续时间的非关键活动，Ⅲ类活动不存在必须占用时段。如图1中活动C，其持续时间为10 d，总时差为12 d，总的活动时间范围为10～32，可能的位置方案总共有TFC+1=13种，这13种位置方案不存在共同的必须占用时段。

通过以上分析可知，Ⅰ类活动和Ⅱ类活动在必须占用时段对资源的需求在时间和数量上均固定不变，我们把这部分资源需求构成的直方图称为基础资源直方图。例如图2，活动A、C、E、G、H为Ⅰ类活动，F为Ⅱ类活动，18、19两天为其必须占用时段，它们共同构成项目的基础资源直方图，即图2中灰色部分，下方数字Rt为在时段t项目基础资源需求数量。

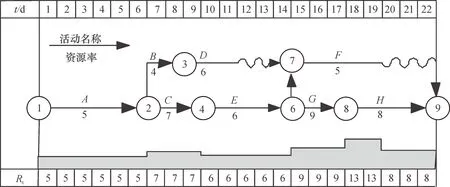
图2　时标网络计划和基础资源直方图

基础资源直方图代表了项目计划对资源需求的不可变动部分，最终的资源分布情况主要取决于对Ⅱ、Ⅲ类非关键活动位置决策。这一决策过程可以想象为在一个底部不平的“容器”内进行装箱，并希望最终箱内所装“物品”的高度尽可能低平。因此，一个很自然的想法就是依次选出那些对资源分布改变比较大的活动，然后逐一将其安置在“容器”的最低凹处。

2.2活动优先规则

活动优先规则决定对Ⅱ、Ⅲ类活动位置安排的先后顺序。文献中可见到各种不同的优先排序规则：Harris[17]采用改进因子IF(improvement factor)对活动进行排序；Hiyassat[18]则证明活动资源率对IF具有决定性影响作用，故而首先按照资源率对活动进行排序；此外，还有文献按照活动的自由时差大小和活动持续时间大小进行排序[20]，但是都无法从数学上对其最优性进行严格的证明。结合文献中已有排序准则，本文采用的优先规则如下：

1) 按非关键活动资源率从大到小排列；

2) 资源率相同时，按总时差从小到大排列；

3) 总时差相同时，按活动时间长短，从大到小；

4) 活动时间长短相同时，按照最早开始时间从小到大；

5) 以上都相同时，顺序任意。

2.3活动位置方案选择

活动优先序确定后，接下来的工作就是按活动列表逐一安排活动的位置。初始状态下，活动Ai的可占用的时间范围为ESi～LFi，总的位置方案数为TFi+1个，具体位置方案用其开始时间标记：STi,τ=ESi+τ(τ=0,…,TFi)。计算每一个可能位置方案对应的基础资源直方图中的资源数量和∑Ri, τ，作为该方案的评价值，如式(8)所示。评价值最小的方案所对应的位置即为选定方案，即sti=min{STi,τ},τ=0,…,TFi。

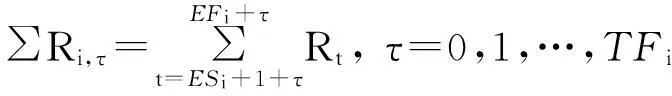
(8)

当活动位置方案评价值同时存在几个相等最小值时，需要进一步计算其紧前活动和紧后活动可行位置方案评价值的最小值并求和，和值最小的方案为最终位置方案。例如，图2中活动D的开始时间在9、10、11时，评价值均为18；进一步计算其紧前活动B和紧后活动F的评价值，活动B的最小评价值分别为14、13、12，活动F的最小评价值保持为50不变，B、F两个活动最小评价值的和分别为64、63、62，由此，可以确定活动D的开始时间应当确定为11。如果经过计算最小评价值的和仍存在相同情况，取开始时间最小的方案为最终位置方案，以获得更好的工期保障。

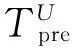
图3　活动D定位后基础资源直方图

2.4资源均衡优化基本步骤

本文所采用的资源均衡优化步骤描述如下：

1)构建网络，确定活动之间的逻辑关系。计算活动时间参数，包含ES、EF、LS、LF和TF。

2)确定Ⅰ类活动和Ⅱ类活动必须占用的时段，绘制基础资源直方图。

3)按照2.2中的优先规则，对所有的Ⅱ、Ⅲ类活动排序，建立活动处理列表。

4)选择活动处理列表中的第一个活动，计算该活动每个可能位置方案评价值，选择评价值最小的方案定位该活动；当存在多个相同最小值方案时，计算其紧前活动和紧后活动的最小评价值，选择评价值和最小的方案；如果评价值和仍相同，取其中开始时间最小的方案。

5)第一个活动定位后，更新资源直方图，将该活动位置方案所对应的资源率添加至资源直方图，同时更新其紧前活动和紧后活动的时间范围，然后从活动处理列表中删除此活动。

6)依次选择活动处理列表中的活动，重复步骤4)、5)，直至所有非关键活动的位置被定位，绘制最终资源直方图。

3指派约束和技能人员指派优化

3.1活动重叠关系与指派约束

当调度方案确定后，便可根据活动之间的时间关系，判定活动之间是否存在重叠关系。如图4所示，当活动Ai与活动Aj之间的时间关系满足式(9)时，便可判定二者之间存在重叠关系，记为{Ai||Aj}。以此类推，如果存在多个活动相互共同重叠时，则重叠关系判定条件可表示为式(10)，记为{Ai||Aj||Aj′||…}。

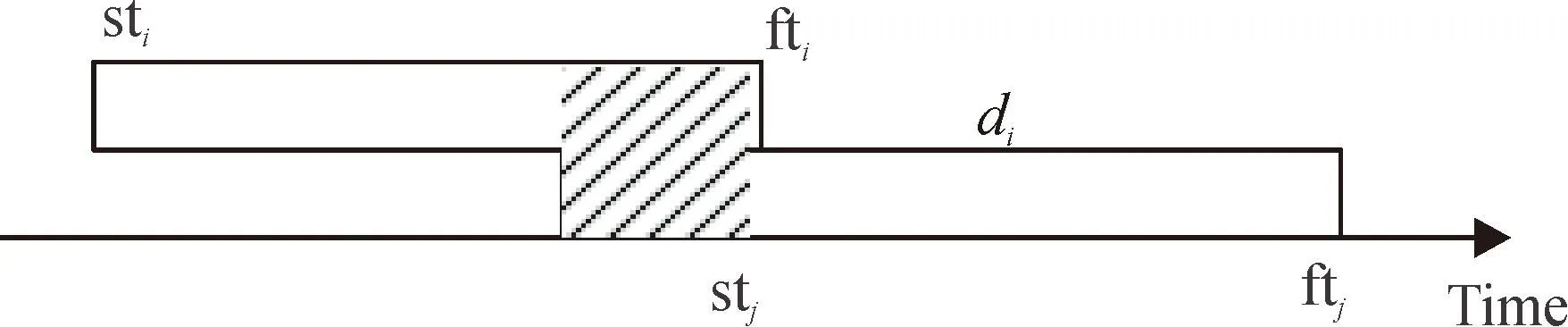
图4　活动重叠关系图

max{sti,stj}

(9)

max{sti,stj,stj′,…}

(10)

通过活动时间分析，可以把一个确定的调度方案中所有的重叠关系活动集合判定出来，记为ο(A)。根据假设不能把一个人同时安排给多个相互重叠的活动，因此，对应于式(9)和式(10)的重叠关系，转化为相应的人员指派约束可分别表示为式(11)和式(12)。

xm,i,k+xm,j,k′≤1,

(11)

xm,i,k+xm,j,k′+xm,j′,k″+…≤1。

(12)

3.2人员指派优化模型

经过第2部分人力资源均衡优化，资源直方图中最高峰用量得到有效降低。此时，可认为原问题中对优化目标有影响的第一个方面的因素，即活动时间调度对技能人员需求的影响问题得到解决。接下来需要解决人员指派优化问题，即在需求分布确定的情况下，如何用最少的人完成项目任务。

在调度方案确定的情况下，原问题模型可简化为下列指派问题模型：

(1)

s.t.

(2)

(3)

θ(X)≤1。

(13)

其中，目标函数(1)与束条件(2)(3)的含义均不变，式(13)表示时间上相互重叠的活动集合ο(A)对应的人员指派约束集合。这是一个典型的指派整数规划模型，求解该问题的线性规划松弛问题即可得到整数最优解。

4算例实验

为了验证本算法可行性，本文采用网络计划生成软件RanGen1[21]来生成本算法的测试算例。考虑一般的网络复杂度，该算例生成参数设置如下：活动数为30，次序强度OS=0.3，活动复杂指数CI=0.5，资源种类为8，可理解为该项目的执行需要8种技能，资源因子RF=0.3，资源强度RS=1。另一方面，为确保问题有解，给定一个足够大的人力资源池，包括100个人，每人同时掌握3种技能，每种技能掌握的人数不少于30人。

图5　资源均衡优化后的调度方案

首先采用本文第2部分的启发式方法，在工期固定的情况下，对各项活动所需的总人力资源的数量进行均衡优化。均衡优化的结果如图5所示，图6为该进度计划所对应的各类技能人员需求总和的变化曲线，图中最高峰人数需求为68人，最低谷的需求用量为19人。

针对相同的调度方案，把人力资源池中人均技能数量调整为1和2，重新进行指派优化，结果总的人员需求数量分别为163人和81人。由此可见，当由单技能变为双技能时，人员用量减少非常显著，对人力资源成本的降低作用非常明显，但是，当从双技能变为3技能时，人员用量的减少的幅度明显降低。考虑到人员技能获得需要一定成本，在项目多技能人力资源调度与指派问题中，并非人均技能数量越多越好，如何合理组合人员的多技能将是未来值得进一步研究的问题。

图6　资源均衡优化调度方案对应的资源需求

Fig.6Resources demand corresponding to the scheduling scheme being leveled

5结论

在项目多技能人力资源调度和指派问题中，影响人力资源使用数量的因素主要有两方面：一方面，项目活动时间调度决定项目对人力资源需求的分布，既定调度方案下资源直方图中最高峰的用量构成人员指派优化最优解的下界。对此，本文提出的资源均衡优化启发式方法简单易懂，便于操作，能有效降低最高峰人力资源需求用量，并可用来求解实际工作中的大规模问题。另一方面，在调度方案确定的基础上，活动之间的重叠关系决定了指派方案的可行性。通过本文的活动时间分析方法，可识别重叠活动对人员指派的有效约束，将这些约束添加至指派问题模型，可有效缩减指派问题的可行域，提高问题的求解效率，从而获得既定调度方案下的最优人员指派。算例实验表明使用该方法可提高人力资源的使用效率，降低项目人力资源成本，为项目管理者提供决策帮助。

参考文献：

[1]GOMAR J E, HAAS C T, MORTON A D P. Assignment and allocation optimization of partially multiskilled workforce[J]. Journal of Construction Engineering and Management, 2002, 128(2): 103-109.

[3]寿涌毅. 资源受限多项目调度的模型与方法[M]. 杭州: 浙江大学出版社, 2010.

[4]BRUCKER P, DREXL A, MOHRING R, et al. Resource-constrained project scheduling: Notation, classification, models, and methods[J]. European Journal of Operational Research, 1999, 112(1): 3-41.

[5]DENISE S Y, VINCIUS A A, MANUEL L. Robust optimization models for project scheduling with resource availability cost[J]. Journal of Scheduling, 2007, 10(1): 67-76.

[6]HARRIS R B. Packing method for resource leveling[J]. Journal of Construction Engineering and Management, 1990, 116(2): 331-350.

[7]WIESEMANN W, KUHN D, RUSTEM B. Maximizing the net present value of a project under uncertainty[J]. European Journal of Operational Research, 2010, 202(2): 356-367.

[8]BELLENGUEZ M O, NÉRON E. A branch-and-bound method for solving multi-skill project scheduling problem[J]. RAIRO Operation Research, 2007, 41(2): 155-170.

[9]HEIMERL C, KOLISCH R. Scheduling and staffing multiple projects with a multi-skilled workforce[J]. OR Spectrum, 2010, 32(2): 343-368.

[10]ALFARES H K, BAILEY J E. Integrated project task and manpower scheduling[J]. IIE Transactions, 1997, 29(9): 711-717.

[11]WU M, SUN S. A project scheduling and staff assignment model considering learning effect[J]. The International Journal of Advanced Manufacturing Technology, 2005, 28(11/12): 1190-1195.

[12]ATTIA E, DUQUENNE P, LE-LANN J. Considering skills evolutions in multi-skilled workforce allocation with flexible working hours[J]. International Journal of Production Research, 2014, 52(15): 4548-4573.

[13]CORREIA I, SALDANHA-DA-GAMA F. The impact of fixed and variable costs in a multi-skill project scheduling problem: An empirical study[J]. Computers & Industrial Engineering, 2014, 72: 230-238.

[14]卢鹏宇，孙文俊，井瑞. 基于时间片段的多IT项目人力资源调度问题求解[J]. 系统工程理论与实践, 2012, 32(4): 731-737.

LU Pengyu, SUN WenJun, JING Rui. Time slice based solution for human resource scheduling problem of multiple IT projects[J]. Systems Engineering-Theory&Practice, 2012, 32(4): 731-737.

[15]LI H, WOMER K. Scheduling projects with multi-skilled personnel by a hybrid MILP/CP benders decomposition algorithm[J]. Journal of Scheduling, 2009, 12(3): 281-298.

[16]BELLENGUEZ M O. Methods to solve multi-skill project scheduling problem[J]. Journal of Operations Research, 2008, 6(1): 85-88.

[17]HARRIS R B. Precedence and arrow networking techniques for construction[M]. New York: Wiley, 1978.

[18]SALEM Hiyassat M A. Modification of minimum moment approach in resource leveling[J]. Journal of Construction Engineering and Management, 2000, 126(4): 278-284.

[19]HEGAZY T. Optimization of resource allocation and leveling using genetic algorithms[J]. Journal of Construction Engineering and Management, 1999, 125(3): 167-175.

[20]HIYASSAT M A S. Applying modified minimum moment method to multiple resource leveling[J]. Journal of Construction Engineering and Management, 2001, 127(3): 192-198.

[21]RANGEN. http://www.projectmanagement.ugent.be/?q=research/RanGen.[OL].

[22]ILOG. IBM ILOG OPL V6.3 IBM ILOG OPL Language Reference Manual[M]. Copyright International Business Machines Corporation, 1987, 2011.

Methods of Assigning Multi-skilled Human Resources and Scheduling Projects Based on Resource Leveling

LI Ming1,2，XU Zhe2

(1. School of Economics and Management, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. School of Economics and Management, Beihang University, Beijing 100191, China)

Abstract：To improve the efficiency of human resources used in the project, an optimization method of assigning multi-skilled human resources and scheduling projects is put forward. First of all, with a heuristic algorithm presented to level the human resources, a scheduling scheme with low peak in human resource requirement can be obtained. Then, based on the determined scheme, the overlapping relationships between activities are identified and converted to a series of effective constraints to assigning multi-skilled human resources. Finally, an integer programming model is established and calculated by programming. The research results show that the method can be used to quickly find a near optimal solution of the problem, using less human resource to complete the tasks, and reduce the cost of human resources effectively.

Key words：human resources; resource leveling; multi-skill; project scheduling; assignment

中图分类号：TL372

文献标志码：A

文章编号：1007-7375(2016)01- 0108- 07

doi:10.3969/j.issn.1007- 7375.2016.01.017

作者简介：李明(1975-)，男，副教授，博士研究生，主要研究方向为项目管理.

基金项目：国家自然科学基金资助项目(712710191)；河北省社会科学基金资助项目(HB14GL023)；河北省高等学校科学技术研究项目(QN2014035)；河北省科技计划项目(13456119D)。

收稿日期：2015- 12- 02