无轴承异步电动机悬浮子系统独立鲁棒控制方法研究

孙宇新　钱忠波

(江苏大学电气信息工程学院　镇江　212013)



无轴承异步电动机悬浮子系统独立鲁棒控制方法研究

孙宇新钱忠波

(江苏大学电气信息工程学院镇江212013)

摘要为实现无轴承异步电动机(BIM)的动态解耦控制，基于径向基函数神经网络(RBFNN)，提出一种悬浮子系统独立鲁棒控制方法。应用RBFNN辨识系统模型不确定因素和外界干扰，基于HJI不等式原理设计RBFNN鲁棒控制器，实现悬浮子系统的动态独立解耦控制，并提高系统的稳定性和抗干扰性能。仿真和实验结果表明所提出的BIM控制系统具有良好的动静态性能。

关键词：无轴承异步电动机悬浮子系统独立控制鲁棒控制器HJI不等式径向基函数神经网络

0引言

依靠转矩绕组和悬浮力绕组磁场的共同作用，无轴承异步电动机(Bearingless Induction Motor，BIM)可实现笼型转子的稳定悬浮，具有结构简单、易于弱磁以及可靠性高等优点，非常适合应用于高速精密数控机床及高压密封泵等高速驱动的高新技术领域，因而受到了国内外学者的广泛关注。然而，BIM的多套绕组之间存在复杂的电磁关系，使得解耦控制成为实现BIM稳定悬浮和转矩输出的关键问题。

自BIM被提出以来，众多专家学者已对悬浮力和转矩解耦控制进行了大量研究。转矩绕组气隙磁场定向控制方法是目前控制无轴承异步电动机较为成熟的控制方法之一，但该方法需要在两套绕组控制子系统之间传递转矩绕组的气隙磁链信息，所以并未实现真正意义上的独立解耦控制[1]。其次，因其本身机理的制约存在最大转矩限制[2]，从而影响其在重载和大功率条件下的应用。此外，逆系统、支持向量机和静态神经网络方法也被陆续应用到非线性系统解耦控制中[3-7]。然而，传统逆系统解耦控制方法需要获得被控对象的精确数学模型，而无轴承异步电动机属于多变量、非线性、强耦合系统，其数学模型随其运行状态随时发生改变，导致传统逆系统方法很难在实际中得到应用。基于静态神经网络的逆系统解耦控制方法能够使无轴承异步电动机系统获得良好的动静态性能[3-4，8]，但其系统结构复杂、输入变量多、实现相对困难。文献[9]提出将滑模观测器应用到无位置和无速度传感器控制中，摆脱了传统基于电动机模型的无速度、无位置传感器对电动机参数的依赖，增强了系统的鲁棒性能。文献[10]对短路容错控制在无轴承永磁同步电动机中的应用进行了可行性分析，为提高无轴承电动机控制安全性和鲁棒性提供了一条新思路。文献[11]提出了一种悬浮子系统独立控制方法，通过电压模型辨识方法辨识出悬浮绕组独立控制条件下的转矩绕组气隙磁链幅值和相位，使转矩绕组摆脱悬浮原理约束，提高了调速方法的灵活性。更为重要的是，这种方法不仅能实现悬浮力和转矩之间解耦，使得BIM具有良好的动静态性能，还具有算法简单及极易实用化等特点。

为实现无轴承异步电动机的动态解耦控制，本文提出了一种基于径向基函数(Radial Basis Function Neural Network，RBFNN)和HJI(Hamilton-Jacobi-Isaacs)不等式原理的悬浮子系统独立鲁棒控制方法。该方法通过气隙磁链辨识器辨识出实现独立控制所必须的精确气隙磁链，同时基于HJI不等式原理设计了RBFNN鲁棒控制器，最后建立控制系统以实现悬浮绕组子系统的独立控制，使控制系统具有更强的抗干扰能力；转矩绕组子系统则通过普通变频器控制，增强了控制方法的实用性。仿真结果和实验表明，该独立控制方案能够使无轴承异步电动机系统具有良好的控制性能和较强的鲁棒性。

1无轴承异步电动机基本机理

1.1基本原理

BIM集磁轴承和电动机功能于一体，能同时实现转子悬浮和旋转功能，是特种传动应用领域采用无轴承支承运行的最具有发展前途的方案之一[12]。从结构上分析，无轴承异步电动机通过在原有的定子绕组中添加一套径向力绕组，通过两套不同极对数绕组磁场的相互作用，使异步电动机气隙合成磁场的对称性发生改变，从而在转子上产生可控径向力，实现转子的稳定悬浮和旋转。

悬浮绕组的引入打破了电动机原有旋转磁场的平衡，使得电动机气隙中一个区域内的磁场增强，其对称区域的磁场减弱，产生的麦克斯韦力指向磁场增强的方向。如图1所示，分别向转矩控制绕组和悬浮控制绕组中通入电流I1和I2，产生磁链ψ1和ψ2。

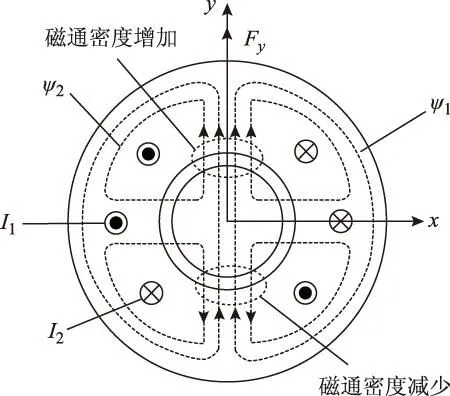
图1　径向悬浮力产生原理Fig.1　Generation principle of radial suspension force

在忽略负载的情况下，由于在气隙上侧ψ1和ψ2同向，合成磁通密度会增加；在气隙下侧ψ1和ψ2反向，则合成磁通密度会减少，从而磁拉力的分布发生改变，产生沿y正方向的径向悬浮力Fy。在悬浮控制绕组中通入反向电流，可产生沿y负方向的径向悬浮力。同理，沿x轴方向的径向悬浮力Fx可通过在悬浮控制绕组中通入与I2垂直的电流获得。

1.2径向悬浮力数学模型

当悬浮绕组极对数P2与转矩绕组极对数P1满足P1=P2+1时，洛伦兹力(用F1表示)和麦克斯韦力(用Fm表示)方向相同，令F(F=Fm+Fl)为悬浮力的可控分量，在d、q轴旋转磁场坐标系下用磁链表示的悬浮力公式为

(1)

式中，ψd1、ψq1分别为气隙磁链分量；K=Km+Kl，其中Km为麦克斯韦常数，Kl为洛伦兹力常数；下标1、2分别为对应转矩绕组和悬浮控制绕组；下标s为对应定子分量。

当转子发生偏心时，因气隙不均匀造成气隙磁场的不平衡会产生偏心磁拉力，这是一种固有的麦克斯韦力，其表达式为

(2)

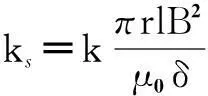
传统BIM径向悬浮力模型多基于理想情况下建立，从而忽略了系统模型不确定性和外界干扰。将系统模型不确定性和外界干扰考虑其中，转子在径向力和外界力作用下的位移运动方程表示为

(3)

式中，m为转子质量；dx、dy分别为模型不确定性以及外界干扰。

对气隙磁场进行定向控制，则有

ψd1=ψ1, ψq1=0

(4)

将式(4)代入式(1)可简化为

(5)

由式(5)可得出悬浮绕组电流与悬浮力之间的关系，根据悬浮绕组电压和电流之间的非线性关系再映射出Ud2s和Uq2s。

2气隙磁链辨识方法

由于径向悬浮力的控制只与转矩绕组气隙磁链的幅值和相位相关，因此若能有效探测或辨识该磁链的幅值和相位，便能实现悬浮子系统的独立控制[11]。因此，对气隙磁链幅值和相位的精确辨识是能够实现独立控制的关键。

2.1转矩绕组气隙磁链数学模型

转矩绕组的定子磁链在静止等效α、β坐标系下有

(6)

式中，ψα1s、ψβ1s分别为定子磁链在α、β轴方向分量；Uα1s、Uβ1s分别为定子电压在α、β轴方向分量；iα1s、iβ1s分别为定子电流在α、β轴方向分量；R1s为转矩绕组的定子电阻。

转矩绕组气隙磁链在α、β坐标系中满足

(7)

式中，L1sl为转矩绕组的定子漏感。

2.2气隙磁链辨识电压模型法

电压模型法通过式(6)和式(7)计算气隙磁场，图2为气隙磁链辨识框图。

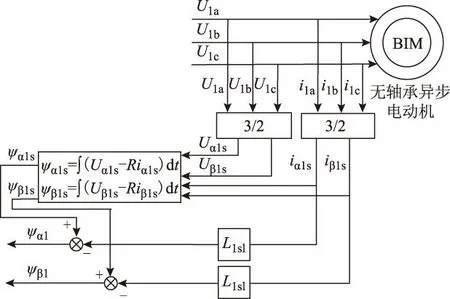
图2　气隙磁链辨识框图Fig.2　Identification of airgap flux linkage

采用图2所示的气隙磁链辨识模型可通过采集电压电流信号在线辨识出气隙磁链值，为实现悬浮子系统独立控制提供前提。

3独立鲁棒控制系统

文献[13]研究表明带模有界条件的非线性不确定系统，在适当的正则性假设下，其鲁棒可镇定性完全可由一个扩展的HJI微分不等式是否存在正解来确定。本文基于HJI不等式原理对无轴承异步电动机悬浮子系统进行控制，以实现转矩子系统采用通用变频器控制时悬浮子系统独立控制，且转矩子系统以及悬浮子系统具有较强的鲁棒性。

3.1HJI不等式定理

针对如下模型

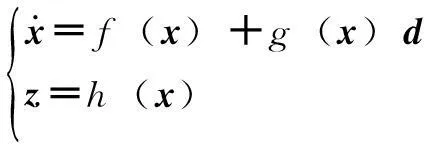
(8)

式中，d为外界干扰；z为系统的评判指标。

定义：对于信号d(t)，其L2范数为

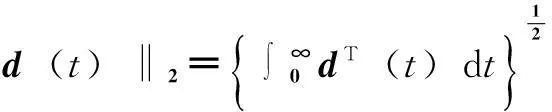
(9)

该范数可衡量d(t)的能量大小。

为了评判系统的干扰抑制能力，定义如下性能指标

(10)

式中，J为系统的H∞增益，表示系统扰动抑制性能，J越小表示系统的扰动抑制性能越强。

根据文献[14，15]中定理2和式(8)，HJI定理可描述为：对一个正数γ，如果存在一个正定且可微的函数L(x)≥0且

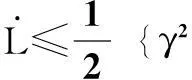
(11)

当式(11)对于任意的d都成立，则J≤γ。

3.2鲁棒控制器设计

将HJI不等式应用于神经网络鲁棒控制器中能有效改善系统稳定性，因此本文提出一种基于HJI不等式原理的鲁棒控制器，通过RBFNN辨识系统模型不确定因素以及外界因素[16]，以实现对BIM悬浮子系统的独立解耦控制。将本文闭环系统式(3)改写为矢量形式

(12)

式中，z为位移矢量。

假设理想跟踪位移为zd，跟踪误差e=z-zd，设计前馈控制律为

(13)

式中，u为反馈控制律。

将式(13)代入式(12)可得

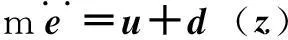
(14)

采用RBF神经网络逼近d(z)，其表达式为

(15)

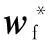
综合式(14)和式(15)得

(16)

定义

(17)

式中，若α>0，则

(18)

利用HJI不等式将式(18)写成如下形式

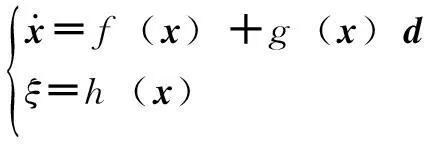
(19)

式中

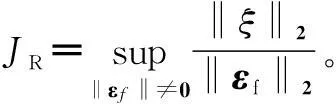
设计如下自适应律

(20)

式中，η为正实数。

设计反馈控制律为

(21)

由HJI不等式定理可得，设计后的闭环系统满足J≤γ， 是稳定的[17]。

3.3控制系统设计

为了实现系统良好的动静态性能，本文提出了一种基于RBFNN和HJI不等式的自适应鲁棒控制器的悬浮子系统独立鲁棒控制系统，如图3所示，其中M=1/Kψ1。

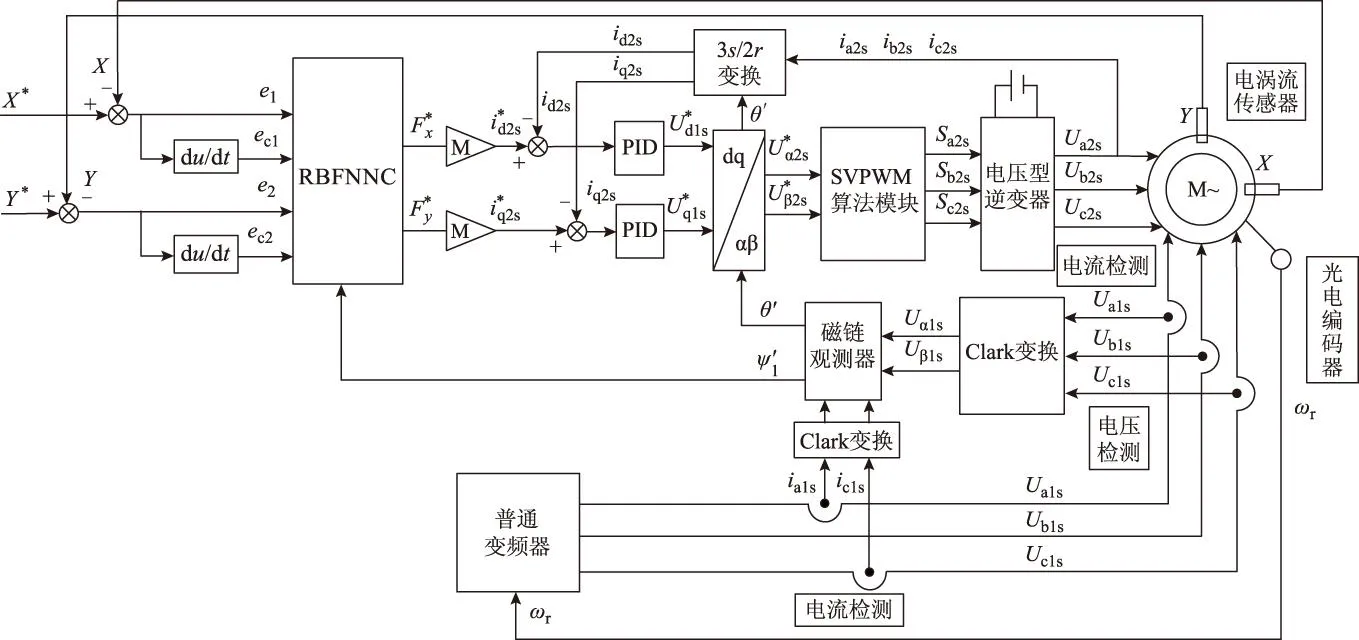
图3　悬浮子系统独立鲁棒控制系统框图Fig.3　Independent robust control system for levitation subsystem

与传统气隙磁场定向以及传统悬浮子系统独立控制系统相比，本文创新点在于基于HJI不等式原理的鲁棒控制器设计及悬浮子系统独立鲁棒控制系统的建立，具有如下特点：

1)运用气隙磁链观测辨识出气隙磁链值，使实现高性能独立控制成为可能，转矩子系统则可使用通用变频器控制，增强了BIM的实用性。

2)设计基于HJI不等式原理和RBFNN的鲁棒控制器取代传统的PID控制器，减少了参数调节，增强了系统的鲁棒性能和控制准确度。

3)内环采用PID电流滞环，加快了反应速度。

4)采用SVPWM算法代替传统的SPWM算法，增加了电压利用率，具有一定优势。

4系统仿真与实验分析

以一台无轴承异步电动机试验样机为研究对象，首先通过Matlab建立仿真模型来验证本文提出的控制策略的有效性。控制器取4-7-2结构的RBF神经网络，η=1 500，α=20，γ=0.05，高斯函数参数ci和bi分别为[-1.5-1-0.500.511.5]和10，并进行仿真实验。系统参数如表1所示。

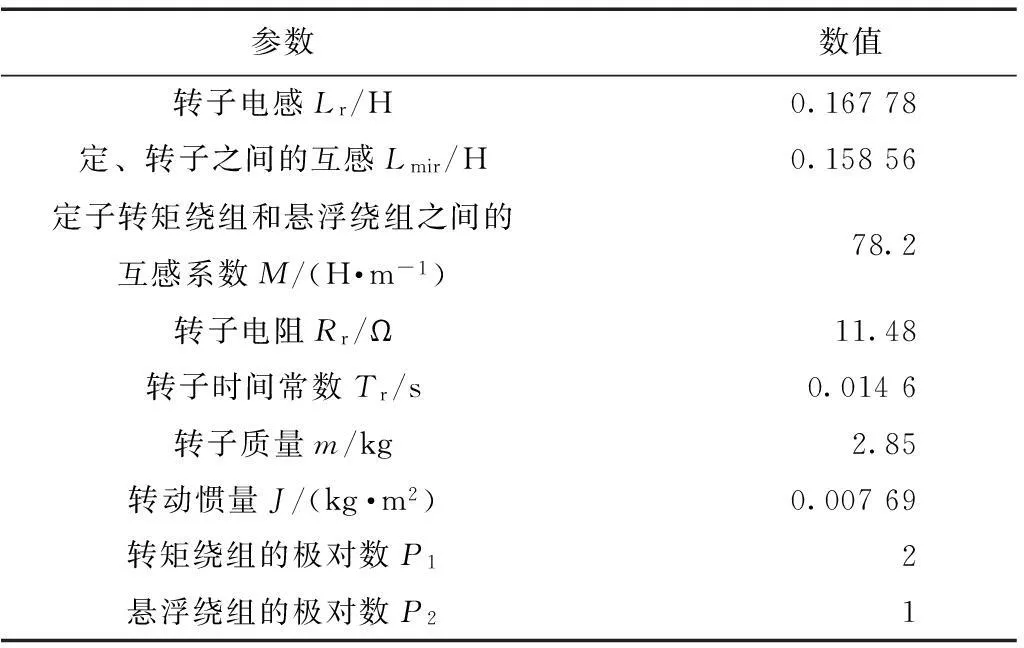
表1　电动机参数

由于径向悬浮力的控制只与转矩绕组气隙磁链的幅值和相位有关，采用独立控制后转矩子系统摆脱悬浮原理束缚，所以转矩绕组就近似于一个独立的异步电动机模型，仿真中采用变频器控制转矩绕组，转子转速波形如图4所示。在0.5 s给定转速由3 600 r/min突加至7 200 r/min。图4中，电动机起动后，转子转速迅速到达给定转速3 600 r/min，调节时间约为0.01 s，几乎没有超调，且保持稳定；当转速给定突变至7 200 r/min，转子转速迅速响应，调节时间约为0.01 s，具有良好的动静态性能。悬浮绕组由本文提出的独立鲁棒解耦控制算法控制，如图5所示，设置转子质心x轴径向位移初始值为-0.08 mm，y轴径向位移初始值为-0.25 mm，初始期望径向位移均为0 mm。由图5a、图5b可知，电动机起动后，转子质心迅速到达给定中心点位置，并保持稳定，位移超调小于0.05 mm，超调时间约为0.06 s。

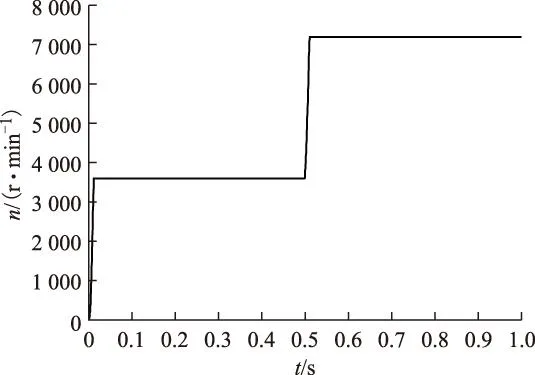
图4　转子转速波形Fig.4　Speed waveform of rotor

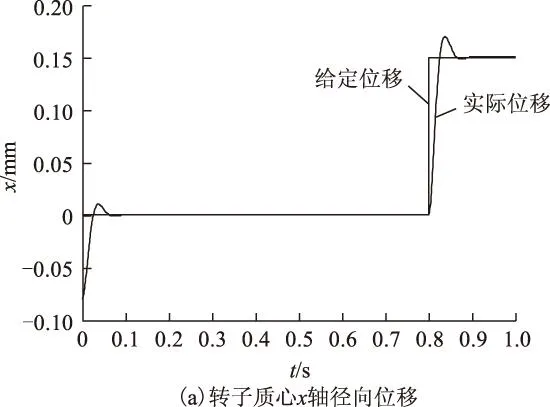
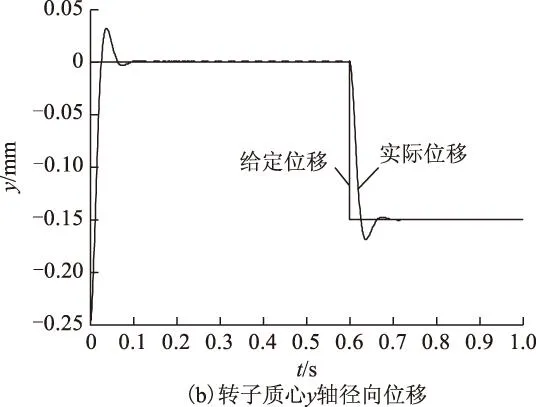
图5　采用本文独立鲁棒控制方法仿真结果Fig.5　Simulating results using independent robust control method

其次，为了检验径向悬浮力子系统在x、y轴方向上的径向悬浮力(径向位移)是否实现解耦控制，在0.8 s调整x轴径向位移为0.15 mm，在0.6 s调整y轴径向位移为-0.15 mm，并与采用传统滞环控制方法进行比较，结果如图5和图6所示。首先比较图5a和图5b可发现，当x轴径向位移发生突变时，y轴径向位移并未受到影响；当y轴径向位移发生突变时，x轴径向位移也未受到影响，因此可得出使用RBFNN鲁棒控制器能够实现x轴和y轴径向力解耦，且系统具有良好的动静态性能。由图4、图5可见，当转速发生突变时，径向位移并未发生明显变化；当径向位移发生突变时，转速也未发生明显变化，仿真表明悬浮子系统独立鲁棒控制方法能够实现转矩和悬浮力之间的解耦。

采用传统滞环控制时转子径向位移最大超调约为0.11 mm，最大超调时间约为0.12 s。比较图5和图6可见，在本文提出方法的控制下，悬浮子系统在运行时转子抖动更小，悬浮性能优异，且具有更好的抗干扰能力。

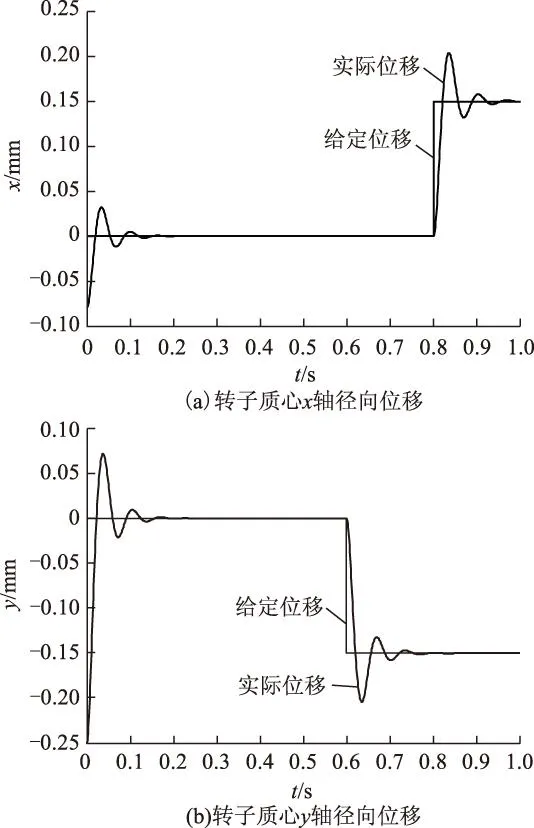
图6　采用传统滞环控制方法仿真结果Fig.6　Simulation results using hysteresis control method

最后，采用本文控制策略，利用实验室无轴承异步电动机数字控制平台对样机进行控制，图7为无轴承异步电动机数字控制平台。

图7　无轴承异步电动机数字控制平台Fig.7　Digital platform for BIM

如图8所示，实验结果表明当转速变化时，电动机转子实现了稳定悬浮，且位移误差小于±50 μm，证明了本文所提方法实现解耦控制的有效性。比较仿真波形和实验波形可知，由于仿真时电动机模型理想化，而实际中电动机加工准确度不高引起转子质量分布不平衡，导致仿真波形的波动程度并没有实验波形明显。此外转子质量分布不平衡导致转子质心不在x、y坐标系原点位置，转子转动时由于x、y轴垂直相位差为90°，在实验中体现为x、y轴方向位移波形相差一定角度，且转速越高波动频率越高，其深层次原因还需进一步研究。为了验证该方法的鲁棒性，在无轴承异步电动机稳定悬浮时，沿径向对轴施加一定压力。如图9所示，突加扰动时，径向位移发生微小变化，短时间内能够迅速恢复到稳定状态，表明能够实现较强的鲁棒控制。此外当y轴方向位移发生突变时，x轴方向位移变化不明显，说明能够实现径向力动态解耦控制。

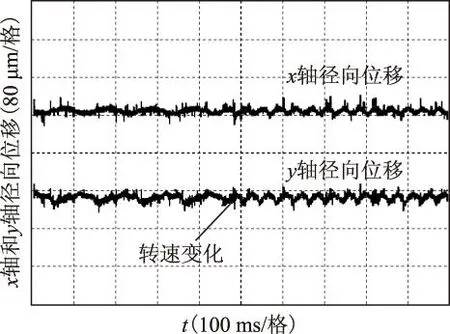
图8　转速变化时转子质心位移实验波形Fig.8　Experimental waveform of rotor centroid displacement when the speed changes

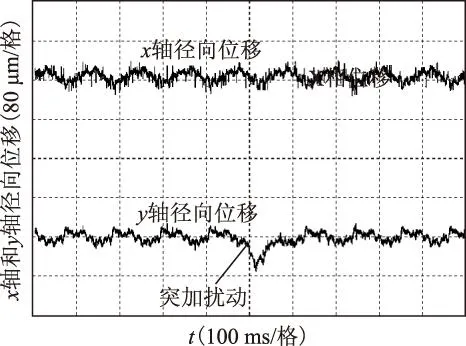
图9　突加扰动时转子质心位移实验波形Fig.9　Experimental waveform of rotor centroid displacement when interrupted

5结论

针对无轴承异步电动机传统悬浮力绕组独立控制系统中鲁棒性差等缺陷，本文提出了悬浮力子系统独立鲁棒解耦控制方法。首先通过磁链辨识方法辨识出悬浮子系统独立控制所必须的气隙磁链值；同时基于HJI不等式原理设计了RBFNN鲁棒控制方法替代传统滞环控制方法，提高控制系统的抗干扰能力及控制性能。仿真和实验结果表明，采用该控制方法不仅能提高无轴承异步电动机的实用性，且控制系统具有良好的动静态性能，为无轴承异步电动机解耦控制提供了一条新思路。

参考文献

[1]Chiba A，Akamatsu D， Fukao T，et al.An improved rotor resistance identification method for magnetic field regulation in bearingless induction motor drives[J].IEEE Transactions on Industrial Electronics，2008，55(2)：852-860.

[2]邓智泉，王晓琳，张宏荃，等.无轴承异步电机的转子磁场定向控制[J].中国电机工程学报，2003，23(3)：89-92.

Deng Zhiquan，Wang Xiaolin，Zhang Hongquan，et al.The nonlinear control of bearingless induction motors based on the motor rotor flux orientation[J].Proceedings of the CSEE，2003，23(3)：89-92.

[3]Sun Xiaodong，Chen Long，Yang Zebin，et al.Speed-sensorless vector control of a bearingless induction motor with artificial neural network inverse speed observer[J].IEEE/ASME Transactions on Mechatronics，2013，18(4)：1357-1366.

[4]Chiba A，Santisteban J A.A PWM harmonics elimination method in simultaneous estimation of magnetic field and displacements in bearingless Induction motors[J].IEEE Transactions on Industry Applications，2012，48(1)：124-131.

[5]孙晓东，朱熀秋.基于神经网络理论无轴承异步电动机解耦控制[J].电工技术学报，2010，25(1)：43-49.

Sun Xiaodong，Zhu Huangqiu.Decoupling control of bearingless induction motors based on neural network inverse system method[J].Transactions of China Electrotechnical Society，2010，25 (1)：43-49.

[6]孙玉坤，周云红，嵇小辅.磁悬浮开关磁阻电机的神经网络逆解耦控制[J].中国电机工程学报，2011，31(30)：117-123.

Sun Yukun，Zhou Yunhong，Ji Xiaofu.Decoupling control of bearingless switched reluctance motor with neural network inverse system method[J].Proceedings of the CSEE，2011，31(30)：117-123.

[7]刘国海，孙玉坤，张浩，等.基于神经网络的磁悬浮开关磁阻电动机的解耦控制[J].电工技术学报，2005，20(9)：39-43.Liu Guohai，Sun Yukun，Zhang Hao，et al.Decoupling control of bearingless switched reluctance motors based on neural network inverse system[J].Transactions of China Electrotechnical Society，2005，20(9)：39-43.

[8]Zhu Huangqiu，Zhou Yang，Li Tianbo，et al.Decoupling control of 5 degrees of freedom bearingless induction motors using α-th order inverse system method[J].Acta Automatica Sinica，2007，33(3)：273-278.

[9]程帅，姜海博，黄进，等.基于滑模观测器的单绕组多相无轴承电机无位置传感器控制[J].电工技术学报，2012，27(7)：71-77.

Cheng Shuai，Jiang Haibo，Huang Jin，et al.Position sensorless control based on sliding mode observer for multiphase bearingless motor with single set of windings[J].Transactions of China Electrotechnical Society，2012，27(7)：71-77.

[10]王晓琳，任新宇，邓智泉，等.短路容错控制在多相无轴承永磁同步电机中的可行性分析[J].电工技术学报，2012，27(3)：105-118.

Wang Xiaolin，Ren Xinyu，Deng Zhiquan，et al.Feasibility of fault-tolerant control of multi-phase permanent magnetic bearingless motors with short-circuited phases[J].Transactions of China Electrotechnical Society，2012，27(3)：105-118.

[11]邓智泉，王晓琳，李冰，等.无轴承异步电机悬浮子系统独立控制的研究[J].中国电机工程学报，2003，23(9)：107-111.

Deng Zhiquan，Wang Xiaolin，Li Bing，et al.Study on independent control of the levitation subsystem of bearingless induction motors[J].Proceedings of the CSEE，2003，23(9)：107-111.

[12]孙晓东，陈龙，杨泽斌，等.考虑偏心及绕组耦合的无轴承永磁同步电机建模[J].电工技术学报，2013，28(3)：64-70.Sun Xiaodong，Chen Long，Yang Zebin，et al.Modeling of a bearingless permanent magnet synchronous motor considering rotor eccentricity and coupling relationship of windings[J].Transactions of China Electrotechnical Society，2013，28(3)：64-70.

[13]王连圭，费树岷.非线性不确定系统的鲁棒镇定与HJI微分不等式[J].控制理论与应用，2000，17(5)：758-762.

Wang Liangui，Fei Shumin.Robust Stabilization for nonlinear uncertain systems and HJI differential inequality[J].Control Theory and Applications，2000，17(5)：758-762.

[14]De Doncker R W，Novotny D W.The universal field oriented (UFO) controller[J].IEEE Transactions Industry Applications，1994，30(1)：92-100.

[15]van der Schaft A J.L2-gain analysis of nonlinear systems and nonlinear state feedback H∞control[J].IEEE Transactions on Automatic Control，1992，37(6)：770-784.

[16]夏长亮，祁温雅，杨荣，等.基于RBF神经网络的超声波电机参数辨识与模型参考自适应控制[J].中国电机工程学报，2004，24 (7)：117-121.

Xia Changliang，Qi Wenya，Yang Rong，et al.Identification and model reference adaptive control for ultrasonic motor based on RBF neural network[J].Proceedings of the CSEE，2004，24(7)：117-121.

[17]刘金琨.RBF神经网络自适应控制MATLAB仿真[M].北京：清华大学出版社，2014.

孙宇新女，1968年生，副教授，研究方向为无轴承电机控制。

E-mail：syx4461@ujs.edu.cn

钱忠波男，1991年生，硕士，研究方向为无轴承异步电动机控制。

E-mail：1078903061@qq.com(通信作者)

Study on Independent Robust Control of Levitation Subsystem for Bearingless Induction Motors

SunYuxinQianZhongbo

(School of Electrical and Information Engineering of Jiangsu UniversityZhenjiang212013China)

AbstractTo realize the dynamic decoupling control for the high-speed bearingless induction motor (BIM), an independent robust control method for the levitation subsystem is proposed based on the radial basis function neural network (RBFNN). The parameter uncertainty and external disturbance of the BIM are identified by the RBFNN. And then the RBFNN robust controller is designed based on the HJI (Hamilton-Jacobi-Isaacs) theory to realize the dynamic decoupling and independent control for the levitation subsystem in order to improve its operation stability and disturbance attenuation performance. The simulation and experiment results show the satisfied dynamic and static performances of the presented control system for the BIM.

Keywords：Bearingless induction motor，the levitation subsystem，independent control，robust controller，Hamilton-Jacobi-Isaacs inequality，radial basis function neural network

作者简介

中图分类号：TM343；TP273

收稿日期2015-11-05改稿日期2016-01-17

国家自然科学基金(61174005)和国家自然科学青年基金(51407085)资助项目。