单层倒悬链型叉筒网壳静力与稳定性研究*

贺拥军，钟　欣，周绪红

(1.湖南大学 土木工程学院，湖南 长沙　410082；2.重庆大学 土木工程学院，重庆　400044)



单层倒悬链型叉筒网壳静力与稳定性研究*

贺拥军1†，钟欣1，周绪红2

(1.湖南大学 土木工程学院，湖南 长沙410082；2.重庆大学 土木工程学院，重庆400044)

摘要：针对以倒悬链线作为交叉柱面准线的单层倒悬链型叉筒网壳，对其常见网格形式结构的静力与稳定性进行比较，得到了结构最佳网格形式.在此基础上，将单层倒悬链型叉筒网壳与圆弧型叉筒网壳进行了静力性能与稳定承载力对比，研究了倒悬链型叉筒网壳的稳定性，包括屈曲模态及杆件截面尺寸、结构几何缺陷、荷载不对称分布与支座约束形式等对结构极限承载力的影响.结果表明，单层倒悬链型叉筒网壳三角形网格形式结构性能最佳；该结构相比圆弧型叉筒网壳具有明显的优越性；初始缺陷对结构稳定性影响较为显著，计算时应考虑1/300跨度的初始缺陷峰值；结构对不对称荷载作用较为敏感；矢跨比为0.50时，网壳的稳定性最好，为最优矢跨比.

关键词：单层倒悬链型叉筒网壳；静力性能；稳定性；极限荷载

叉筒网壳是运用曲面交叉的方式创造出的一种造型新颖的网壳结构形式，一般它利用简单的圆柱面按一定的交贯方法组合而成.近年来学者们在单层叉筒网壳的稳定性研究方面取得了丰硕成果[1-4]，但其研究的叉筒网壳的组成单元均是圆柱面网壳(以圆弧拱为准线)，而对以其他拱准线形式柱面网壳单元所组成的叉筒网壳研究甚少.且上述文献均以正四边形单层圆弧型叉筒网壳作为研究对象，已不能满足现代网壳建设的多样性要求，因此研究更大跨度下其他合理拱准线形式的单层叉筒网壳显得十分必要.悬链线拱在恒荷载作用下,拱截面只承受轴力而无弯矩,截面应力均匀,能够充分利用钢材料的抗压性能[5].依据悬链线拱的这种受力性能,本文将单层倒悬链型柱面网壳的特性与单层叉筒网壳有机地结合起来, 如图1所示，3个相同的倒悬链柱面60°交贯,便形成了单层倒悬链型叉筒网壳结构.

本文针对此种单层倒悬链型叉筒网壳，先分析比较4种不同网格形式的单层倒悬链型叉筒网壳的静力与稳定性，继而确定了一种最优的网格布置形式；然后与单层圆弧型叉筒网壳作对比分析；最后采用参数化分析，较为全面系统地研究了单层倒悬链型叉筒网壳的静力稳定性，包括矢跨比、杆件截面尺寸、初始几何缺陷、荷载不对称分布及支座约束形式等参数对结构极限荷载的影响，以期为该结构形式的工程应用提供理论指导与参考依据.

1计算模型及分析方案

3个相同的圆柱面60°交贯形成的叉筒曲面可覆盖一个正六边形平面，如果每个圆柱面主体采用单层网壳结构，就形成了正六边形圆弧型单层叉筒网壳.根据单层倒悬链型柱面网壳的受力特性，本文以倒悬链型柱面网壳单元替换传统的圆柱面网壳单元，就形成了以倒悬链柱面网壳为单元的单层倒悬链型叉筒网壳.倒悬链型柱面网壳单元的计算模型参考文献[5]，本文利用通用有限元软件ANSYS，仅考虑结构几何非线性的影响，进行网壳结构承载力的全过程跟踪分析.分析中结构杆件均采用BEAM189梁元，网壳节点假定为刚接.

根据常见圆柱面网壳单元杆件的布置方式，本文针对单层倒悬链型叉筒网壳选取了4种网格形式：正放四方网格、斜放四方网格、单斜杆网格以及三角形网格，如图1所示.其中图1(d)中标注的h为结构的矢高，l为结构组成单元的跨度，单位均为m，本文的矢跨比f定义为f=h/l；图1(e)为三角形网格俯瞰图，图中L为整个结构的跨度，单位为m.

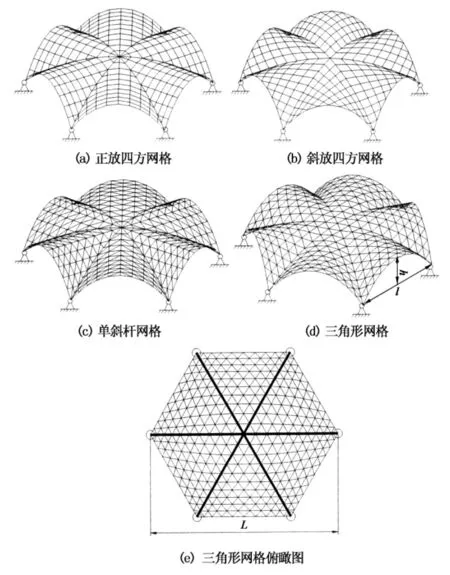
图1　单层倒悬链型叉筒网壳常见网格类型

2单层倒悬链型叉筒网壳最优网格形式的选择

在本节分析中，取跨度为40 m的单层倒悬链型叉筒网壳，谷线拱杆件规格取Ф273×10，其余杆件规格取Ф108×5，网壳矢高5 m，矢跨比h/l=0.25，各交叉谷线两端均三向固定铰支.对图1中4种网格形式分别进行静力与稳定性分析，荷载取2 kN/m2的竖向均布荷载，等效为每个节点竖向18 kN.静力与稳定性分析结果分别见表1和表2.

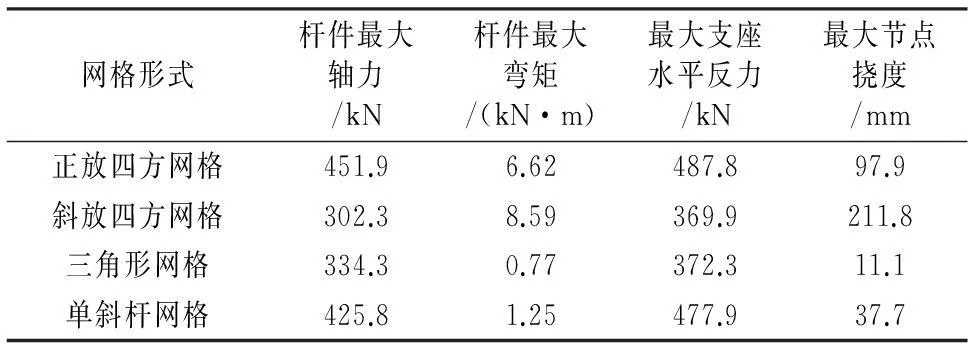
表1　不同网格形式结构静力性能指标对比

表2　不同网格形式结构极限分析对照

由表1可以看出，在相同节点荷载的作用下，三角形网格的杆件最大轴力、最大弯矩，最大支座水平反力及最大节点挠度相比于正放四方网格和单斜杆网格都有降低.并以杆件最大弯矩和节点挠度的降低幅度最为明显.另外，正放四方网格和斜放四方网格的杆件最大弯矩分别达到了6.62 kN·m和8.59 kN·m，相应的杆件弯曲应力已经相当可观.相较之下，三角形网格的杆件最大弯矩仅为0.77 kN·m，弯曲应力很小，杆件内力以轴力为主；从节点挠度角度来看，三角形网格的最大节点挠度仅为11.1 mm，明显低于其他3种网格布置形式.

因不同网格形式下结构用钢量不一致，为了更深入对比分析4种网格形式的优劣，下面从结构稳定性的角度，并考虑用钢量的因素，引入2个与结构极限承载力有关的参数Pt和D.其中Pt为极限承载力与用钢量的比值，即Pt=Pcor/T，该值反映了结构的材料利用情况；D值为文献[3]中所提出的极限荷载下的杆件轴向应力比的平均值，计算公式为：

式中：Ti,Ai,f分别为极限荷载下的杆件轴力、截面面积以及其强度设计值；m为结构内部杆件数量.该D值反映了整个结构杆件材料用量的利用率.

由表2可以看出，三角形网格的稳定性明显优于其他3种网格形式.其Pt值最大，达到了10.11，远高于其他3种网格形式.另外，极限状态下，其他3种网格形式的平均应力比均小于1，说明杆件材料的利用率没有充分发挥出来.当结构采用三角形网格形式时，杆件平均应力比达到1.241 0，杆件材料利用充分，此时结构设计是由强度条件所决定，单位用钢量下结构的极限承载力最高.

通过比较，三角形网格形式的单层倒悬链型叉筒网壳在静力和稳定性方面性能最优，杆件内力基本为轴力，弯矩较小，极限承载力最高，并且充分发挥了杆件材料的利用率，单位用钢量下结构的极限承载力最高.本文以下的深入分析均采用三角形网格形式.

3单层倒悬链型叉筒网壳与圆弧型叉筒网壳性能比较

3.1静力性能

选取结构跨度为40 m，谷线拱杆件规格取Ф273×10，其余杆件规格取Ф108×5，矢跨比分别为0.50,0.45,0.40,0.35,0.30.网壳结构各交叉谷线两端均三向固定铰支，荷载与第2节一致.对单层倒悬链型叉筒网壳进行静力计算，并与圆弧型叉筒网壳作对比，各项静力性能指标对比和静力性能指标降低率的计算结果分别见表3和图2，其中，图2中的静力性能指标降低率=(圆弧型静力性能指标-倒悬链型静力性能指标)/圆弧型静力性能指标.

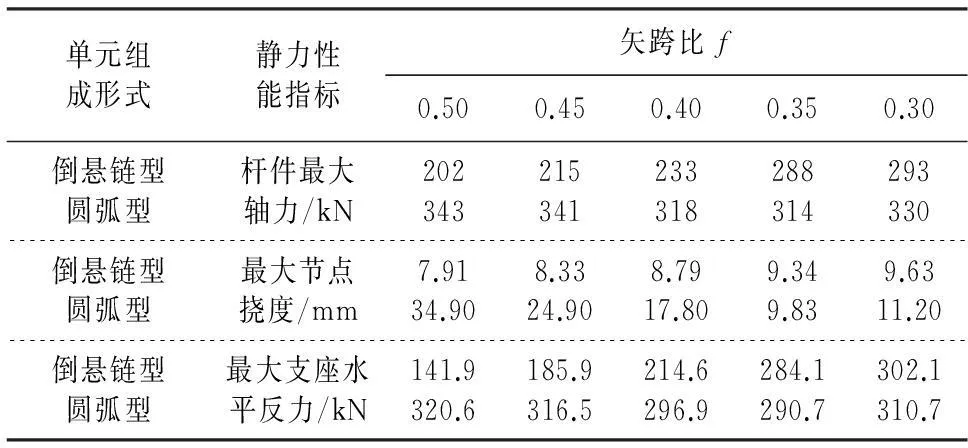
表3　静力性能指标对比

从表3可以看出，在相同的节点竖向荷载作用下，不同矢跨比下的2种单层叉筒网壳结构的各项静力性能指标随矢跨比的变化均呈现出一定的规律，但两者的变化规律各有不同．单层倒悬链型叉筒网壳结构的各项静力性能指标均随着矢跨比的减小而增大,而圆弧型叉筒网壳结构的各项静力性能指标随着矢跨比的减小，以矢跨比f=0.35为临界，呈现出先减小再增大的规律.

根据表3计算出了不同矢跨比下单层倒悬链型叉筒网壳相比于圆弧型叉筒网壳各项静力性能指标的降低率，如图2所示.

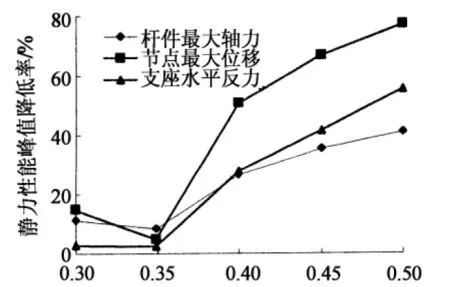
矢跨比

从图2可以看出，单层倒悬链型叉筒网壳的杆件最大轴力、最大节点挠度以及最大支座水平反力相比于圆弧型叉筒网壳均得到了一定程度的降低.各项静力性能指标的降低率随着矢跨比的增大，先缓慢增大，在矢跨比达到0.35时，降低率开始下降，并达到最低，然后在矢跨比增大至0.40时，迅速上升，在0.50时达到最大.

通过以上比较可以看出，当矢跨比小于0.35时，单层倒悬链型叉筒网壳结构相比于圆弧型叉筒网壳结构在降低结构的各项静力性能指标方面，有一定优越性，但降低效果不太显著；当失跨比达到0.35时，2种单层叉筒网壳的静力性能指标最为接近；当矢跨比大于0.35时，单层倒悬链型叉筒网壳在降低结构各项静力性能指标方面表现出了明显的优越性.

3.2稳定承载力

取矢跨比分别为0.50,0.45,0.40,0.35,0.30，对比计算结果如图3所示，其中，图3(b)中的极限荷载提高率=(倒悬链型极限荷载-圆弧型极限荷载)/倒悬链型极限荷载.

从图3(a)可以看出，2种单层叉筒网壳结构极限荷载随着矢跨比变化的分布规律有明显区别，单层倒悬链型叉筒网壳的结构极限荷载随着矢跨比的增大而提高.圆弧型叉筒网壳的结构极限荷载则是在矢跨比从0.30增大至0.35的过程中，迅速增大，在矢跨比为0.35时达到峰值，当矢跨比从0.35增大到0.50的过程中，其极限荷载迅速降低.

矢跨比

矢跨比

从图3(b)可以看出，随着矢跨比的增大，单层倒悬链型叉筒网壳相比于圆弧型叉筒网壳的稳定极限荷载有不同程度的提高．当矢跨比从0.30增加到0.35时，结构的极限荷载提高率随着矢跨比的增大迅速地降低，在矢跨比达到0.35时，结构的极限荷载提高率降低至1.29%，随后，在矢跨比由0.35增大到0.50的过程中，极限荷载的提高率随着矢跨比的增大迅速地增加.在矢跨比为0.50时，达到48.48%．

下面给出2种单层叉筒网壳结构在矢跨比为0.50时的荷载-位移曲线，如图4所示.

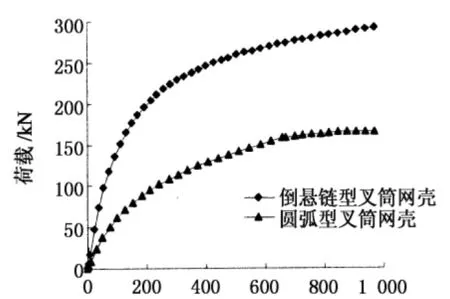
位移/mm

从图4中可以看出，相同矢跨比下，单层倒悬链型叉筒网壳相比于圆弧型叉筒网壳，有效地提高了结构的极限荷载，在相同的节点位移下，单层倒悬链型叉筒网壳具有更高的承载力，整体刚度更高，结构稳定性更好.

综合分析图3和图4可以得出，单层倒悬链型叉筒网壳相比于圆弧型叉筒网壳，有效地提高了结构稳定承载力，在矢跨比等于0.50时，提高效果最为显著.

综上所述，在不同矢跨比下，单层悬链型叉筒网壳相比于圆弧型叉筒网壳，其结构性能更为优越.另外，值得注意的是，对于圆弧型叉筒网壳，在其矢跨比为0.35处性能有突变，这是因为在矢跨比达到0.35时，单层圆弧型叉筒网壳的拱准线曲线形状与倒悬链型叉筒网壳的最为接近，拱截面主要承受轴力，弯矩较小，截面应力均匀，能充分利用钢材料的抗压性能，结构整体刚度达到最大，性能最优.当矢跨比超过0.35后，随着结构整体形状的改变，圆弧型叉筒网壳的拱截面弯矩增大，截面应力不均匀，结构整体刚度降低，从而使得结构静力与稳定性能降低.

4单层倒悬链型叉筒网壳稳定性分析

4.1屈曲模态

至10月10日7时关闭闸门，杜家台分洪闸共开启85小时，共利用行洪道分流汉江下游超额洪水约3.7亿m3，降低仙桃以下河段水位约0.7m。

通过大量参数分析计算发现，单层倒悬链型叉筒网壳在极限荷载作用下发生失稳时，可能出现如下屈曲模态，如图5所示.

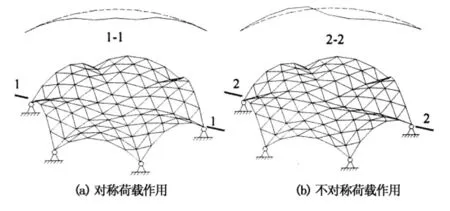
图5　屈曲模态

由图5可知：

1)在对称荷载作用下，单层倒悬链型叉筒网壳中部形成大面积凹陷，谷线部分下凹最为明显，呈现出3个向上凸起的半波形式，如图5(a)所示.

2)在不对称荷载作用下，单层倒悬链型叉筒网壳的屈曲模态表现为荷载作用一侧向下凹陷，另一侧则向外突出隆起，如图5(b)所示.

由此可见，单层倒悬链型叉筒网壳的失稳一般先出现在结构的中部区域，且在谷线处变形最为明显，为其结构失稳最为薄弱的环节.

4.2杆件截面尺寸对极限荷载的影响

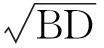
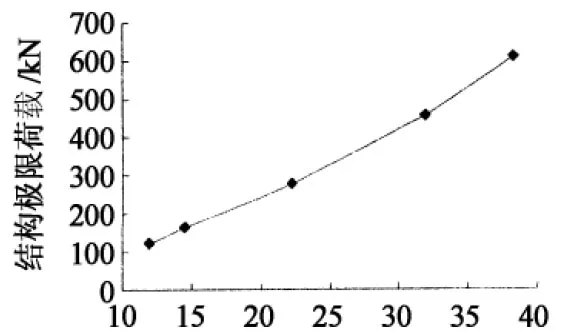
等效刚度/MN

谷线杆件Ф194×10Ф219×10Ф273×10Ф325×10Ф355×10其余杆件Ф83×5Ф95×5Ф108×5Ф127×5Ф140×5等效刚度/MN11.0614.5722.3331.9838.41

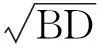
4.3初始几何缺陷对极限荷载的影响

初始缺陷的存在往往会让此种屈曲模态发生一定程度的改变，从而降低整个结构的稳定性[7-8].根据文献[6]中规定,当初始几何缺陷按最低阶屈曲模态分布时,求得的稳定性承载力是可能的最不利值.因此，网壳屈曲模态应与其相应的特征值最低阶屈曲模态相一致.

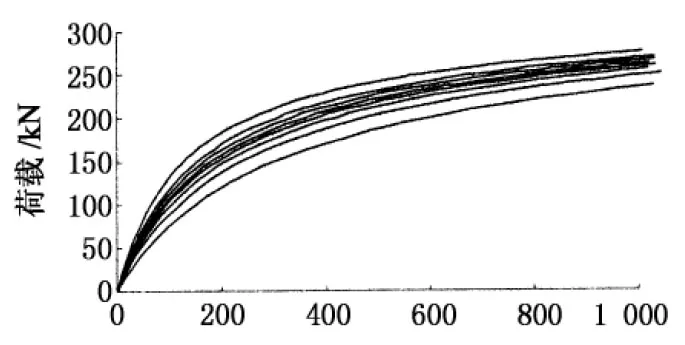
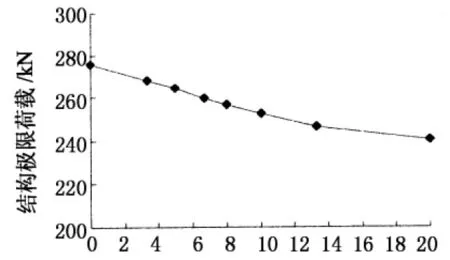
因篇幅限制，本节仅选取矢跨比为0.40的单层倒悬链型叉筒网壳作为分析对象.图7为不同初始缺陷下的全过程曲线及极限荷载变化曲线.图7(a)中曲线自上至下依次为：r=0,L/1 200(3.33 cm),L/800(5 cm),L/600(6.67 cm),L/500(8 cm),L/400(10 cm),L/300(13.33 cm)，L/200(20 cm)

位移/mm

缺陷值/cm

由图7可以看出，当结构的初始几何缺陷从0增加到L/300的过程中，结构的极限荷载随着初始几何缺陷的增大而降低，其变化趋势大致呈线性减小.当初始几何缺陷超过L/300后，结构的极限荷载随着缺陷的增大变幅不大，曲线斜率明显降低，趋于平缓.

根据以上分析可知，初始缺陷值在0到L/300的范围内，对结构极限荷载的影响较为显著.计算时应考虑1/300跨度的初始缺陷峰值.

4.4荷载不对称分布对极限荷载的影响

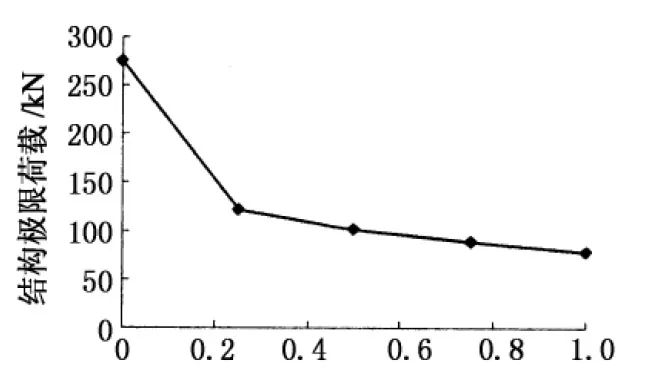
不对称荷载通常是不利的荷载分布，为了研究其对结构极限荷载的影响，本节针对矢跨比为0.40的单层倒悬链型叉筒网壳，按5种不同竖向荷载比例(p/g=0,0.25,0.50,0.75,1.00)的不对称分布形式来进行极限分析.其中g为恒载满跨均布大小，p为活载半跨均布大小.图8给出了不同比例不对称荷载作用下结构极限荷载的变化情况.

p/g

由图8可知，在开始不对称荷载比例较小(p/g=0.25)时，单层倒悬链型叉筒网壳的结构极限荷载随着不对称荷载比例的增大急速下降，从275.6 kN迅速减小到了120.9 kN，降低率达到了56.1%.当不对称荷载比例超过0.25后，极限荷载变化不大.

由此可见，在竖向荷载的作用下，单层倒悬链型叉筒网壳对不对称荷载作用尤为敏感.

4.5支座约束形式对极限荷载的影响

对于单层倒悬链型叉筒网壳，其约束仅为网壳结构各交叉谷线两端角点支撑.由于约束较少，约束形式对网壳的极限荷载会有一定影响.表5给出了不同矢跨比下，不同支座约束形式对极限荷载的影响.其中极限荷载提高率=(固定刚支极限荷载-固定铰支极限荷载)/固定刚支极限荷载.

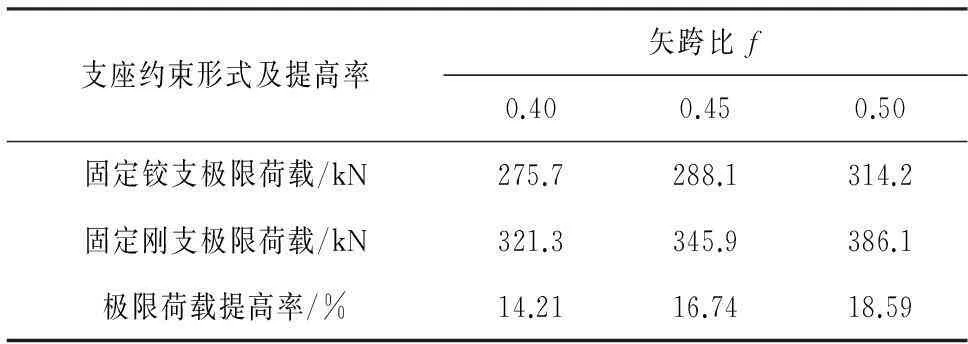
表5　不同支座约束下结构的极限荷载及提高率

从表5可以看出，在不同矢跨比下，对于单层倒悬链型叉筒网壳，其支座约束形式采用固定刚支能够在一定程度上提高结构的极限荷载，并随着矢跨比的提高，其对于结构极限荷载的提高率也在增大.在矢跨比为0.50时，其提高率达到了18.59%.

由此可知，在矢跨比为0.40～0.50时，对于谷线六角点支承的单层倒悬链型叉筒网壳，其支座的约束形式宜采用刚接支座.

5结论

本文主要得出以下结论：

1) 单层倒悬链型叉筒网壳的4种网格形式中，三角形网格形式结构性能最佳.

2) 单层倒悬链型叉筒网壳相比于圆弧型叉筒网壳具有明显的优越性.

3)初始缺陷值在0到L/300的范围内，对结构极限荷载的影响较为显著.计算时应考虑L/300跨度的初始缺陷峰值.

4)单层倒悬链型叉筒网壳对不对称荷载作用尤为敏感.

5)矢跨比为0.50时，单层倒悬链叉筒网壳的稳定性最好，为最优矢跨比.

参考文献

[1]沈世钊,陈昕,张峰.单层柱面网壳的稳定性[J].空间结构，1998,4(2):17-28.

SHEN Shi-zhao, CHEN Xin, ZHANG feng. Stability of single-layer lattice vaults[J]. Spatial Structures,1998,4(2):17-28.(In Chinese)

[2]顾磊,董石麟.叉筒网壳结构的网格形式与受力特性[J].空间结构，2006,12(1):24-32.

GU Lei,DONG Shi-lin.Structural form and behavior of single-layer latticed intersected cylindrical shell[J].Spatial Structures,2006,12(1):24-32. (In Chinese)

[3]贺拥军,周绪红,董石麟.单层叉筒网壳静力与稳定性研究[J].湖南大学学报:自然科学版,2004,31(4):45-50.

HE Yong-jun,ZHOU Xu-hong,DONG Shi-lin.Research on static and stability properties of single layer latticed intersected cylindrical shell[J].Journal of Hunan University:Natural Sciences,2004,31(4):45-50. (In Chinese)

[4]顾磊,董石麟.叉筒网壳的建筑造型、结构形式与支承方式[J].空间结构,1999,5(3):3-11.

GU Lei,DONG Shi-lin.Architectural shapes,structural forms of latticed groined barrel vault and its support metheods[J]. Spatial Structures,1999,5(3):3-11. (In Chinese)

[5]刘旦.单层倒悬链型柱面网壳非线性稳定研究[D].长沙：湖南大学土木工程学院,2012.

LIU Dan.Nonlinear buckling of inverted catenary single-layer cylindrical reticulated shells[D].Changsha: College of Civil Engineering, Hunan University,2012. (In Chinese)

[6]JGJ7-2010空间网格结构技术规程[S].北京:中国建筑工业出版社,2010:74-75.

JGJ7-2010Technical specification for latticed[S].Beijing:China Architecture and Building Press,2010:74-75.(In Chinese)

[7]董石麟,邢栋,赵阳.现代大跨空间结构在中国的应用与发展[J].空间结构,2012,18(1):3-16.

DONG Shi-lin,XING Dong,ZHAO Yang.Application and development of modern long-span space structures in China[J]. Spatial Structures,2012,18(1):3-16. (In Chinese)

[8]张峰,沈世钊.长跨比对单层柱面网壳稳定性的影响[J].哈尔滨建筑大学学报,1998,31(5):26-33.

ZHANG Feng,SHEN Shi-zhao.The effect of length-span rat- io to the stability of single-layer lattice vaults[J].Journal of Harbin University of Civil Engineering and Architecture,1998,31(5):26-33. (In Chinese)

Research on Static Properties and Stability of Single-layer Intersected Inverted Catenary Cylindrical Reticulated Shell

HE Yong-jun1†, ZHONG Xin1, ZHOU Xu-hong2

(1.College of Civil Engineering, Hunan Univ, Changsha, Hunan410082, China;2. College of Civil Engineering, Chongqing Univ, Chongqing400044, China)

Abstract:For the single-layer intersected inverted catenary cylindrical reticulated shell, the static properties and stability of the structures with different types of grid were studied and compared, and then the optimal grid form was obtained. The static properties and stability of the single layer intersected inverted catenary cylindrical reticulated shell were compared with those of the intersected circular cylindrical reticulated shell. Moreover, the stability of the former was studied comprehensively, including the buckling modes and the effect of various parameters such as the member sectional area, initial geometric imperfection, asymmetric load distribution, and support conditions on the ultimate load-carrying capacity. The results show that the structural performance of the single-layer intersected inverted catenary cylindrical reticulated shell with triangular grids is markedly superior to the circular one. Because, this kind of reticulated shell is sensitive to initial geometric imperfection, 1/300 of the structural span should be considered as the initial geometric imperfection value in the calculation of the ultimate load-carrying capacity. Additionally, the reticulated shell is also quite sensitive to the asymmetric load distribution, and the optimal value of rise-span ratio is 0.50 for shell stability.

Key words:single-layer intersected inverted catenary cylindrical reticulated shell; static property; stability; ultimate load

中图分类号：TU356

文献标识码：A

作者简介：贺拥军(1970-)，男，湖南宁乡人，湖南大学教授，博士†通讯联系人，E-mail:hyj0087@163.com

基金项目：教育部博士学科点专项科研基金资助项目(0161110019)；湖南省高校科技创新团队资助计划项目(湘财教指(2012)80号)

*收稿日期：2015-03-09

文章编号：1674-2974(2016)03-0041-07