曲线连续T 型刚构桥应力优化

范琴锋

(中铁四院集团广州设计院有限公司，广东广州　510600)

曲线连续T 型刚构桥应力优化

范琴锋

(中铁四院集团广州设计院有限公司，广东广州510600)

摘要:以穗莞深城际铁路新塘站特大桥为背景，采用Midas civil 2012建立该桥的空间有限元模型，并对调整前后的预应力钢束张拉控制应力进行模拟计算，结果表明:调整曲线梁桥内外侧预应力钢束张拉控制应力，可明显减小曲线梁桥截面内外侧的应力差。关键词: T型刚构桥，曲线梁桥，应力优化

1　工程概况

穗莞深城际铁路新塘站特大桥上跨既有广深铁路的连接线4线采用半径R =410 m的曲线。受既有广深铁路新塘站站场以及规划线的影响，综合考虑桥梁的整体稳定性、墩高较矮、主桥前半部分位于圆曲线与缓和曲线上等情况，主桥采用( 62 +82 +62) m连续T型刚构桥跨越，2号墩为墩梁固结，3号墩与梁之间设置支座。全桥曲线部分采用曲线曲做，主桥桥形布置与平面布置图如图1，图2所示。

图1　（62+82+62）m连续T型刚构桥布置图（单位：cm）

图2　（62+82+62）m连续T型刚构桥平面布置图（单位：cm）

桥梁主要技术标准: 1)设计速度: 80 km/h; 2)线路情况:单线，城市轨道交通; 3)轨道类型:无砟轨道; 4)设计活载: 0.6UIC; 5)地震设防烈度:设计地震动峰值加速度0.1g，地震动反应谱特征周期0.35 s。

2　主要建筑材料

梁体采用C50混凝土，墩采用C40混凝土，桩基础采用C35混凝土;梁体纵向预应力钢束采用17-Φs15.24 mm，15-Φs15.24 mm和12-Φs15.24 mm高强度低松弛钢绞线。箱梁竖向预应力钢筋采用直径32 mm的PSB830螺纹钢筋，JLM-32轧丝锚锚固，内径50 mm铁皮波纹管成孔;梁体普通钢筋采用HRB400。

3　桥梁结构设计

桥梁结构形式采用单箱单室变高度直腹板等宽箱形截面，桥梁跨中及边跨端部截面中心处梁高为4.033 m，中支点截面中心处梁高为7.033 m，箱梁顶宽7.2 m，底板宽5.0 m，顶板厚0.4 m，底板厚0.5 m～1.0 m，其厚度方程为(单位: cm) : d =－4 789.1，x的变化范围为: 0≤x≤3 820;箱梁变化段范围内梁高按圆曲线变化，其截面中心处梁高方程为(单位: cm) : H =403.3 +24 470.7－x的变化范围为: 0≤x≤3 820;腹板厚0.5 m～1.0 m，按折线变化;全联在中支点和边支点处设置端横隔板，在边跨跨中和中跨跨中分别设置30 cm厚的中横隔板，端横隔板和中横隔板均设置过人洞，主梁跨中及墩顶横截面如图3，图4所示。

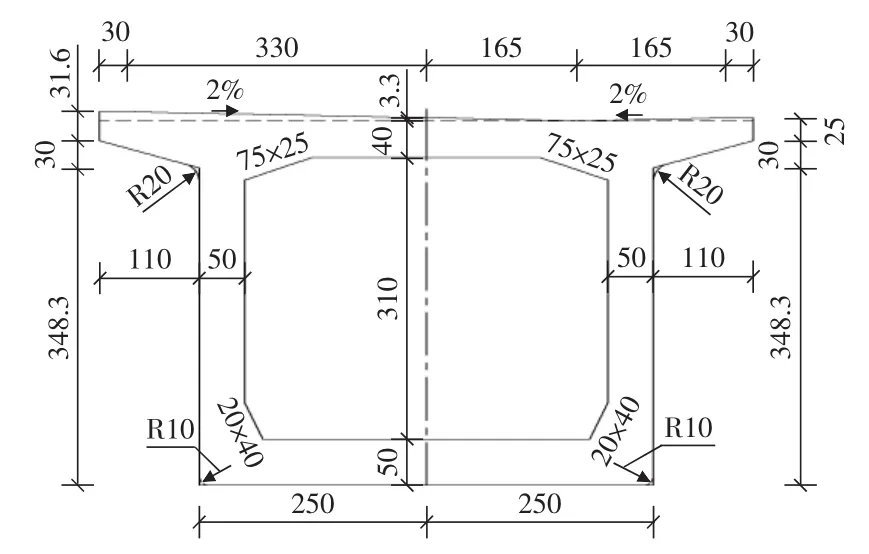
图3　主梁跨中横截面(单位：cm)

桥梁结构按纵、竖双向预应力体系设计，纵向按全预应力构件设计。竖向预应力钢筋在腹板沿顺桥向每50 cm设置一根。

4　施工方法

主梁采用挂篮悬臂现浇法施工，其主要施工顺序如下: 1)依次完成桩基础、承台及墩身施工，架设0号块现浇支架，在支架上施工0号块，待0号块施工完毕后，依次悬臂现浇剩余节段; 2)合龙顺序:先合龙边跨，后合龙中跨; 3)施工桥面系等附属设施，完成全桥施工。

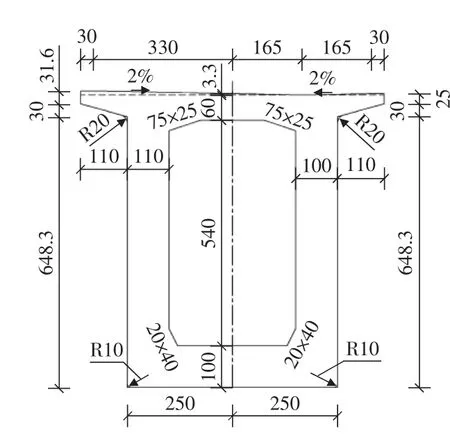
图4　主梁墩顶横截面（单位: cm）

5　截面应力优化计算

1)结构计算模型。

桥梁结构采用Midas civil 2012建立结构空间杆系有限元模型，计算中按照实际的施工顺序进行模拟，全桥共分为175个单元，183个节点;结构有限元模型如图5所示。

图5　桥梁结构三维空间模型

2)计算荷载及参数。

设计活载为0.6UIC，二期恒载单线曲线段按98.5 kN/m、直线段按95 kN/m考虑，基础不均匀沉降为0.15 cm，根据当地气候条件，结构整体升降温按±20℃考虑，主梁顶板升温按10℃、降温按－5℃考虑，其他设计荷载及相关参数按TB 10623—2014城际铁路设计规范取值。

3)应力计算结果比较。

a.钢束张拉控制应力调整前的计算。在模拟计算时，曲线梁内外侧的纵向预应力钢束张拉控制应力均采用0.68fpk=1 264.8 MPa，在运营阶段主+附加力作用下，桥梁跨中底缘正应力见表1。

表1　跨中截面底缘正应力(一)　MPa

从表1的计算结果可以看出，第一跨跨中截面底缘曲线内侧的应力是2.02 MPa，是曲线外侧的2.2倍;第二跨跨中截面底缘曲线内侧的应力是1.2 MPa，是曲线外侧的1.5倍，第三跨跨中底缘曲线内侧的应力与曲线外侧的应力差别不大。从图1可知，第一跨与第二跨位于圆曲线与缓和曲线上，第三跨位于直线上;此外，曲线梁桥由于腹板内短外长，曲线梁桥外侧的腹板受力要比内侧腹板大，因而曲线梁桥曲线外侧的应力比内侧的应力要小，并且曲率越小，截面内外侧的应力相差越大。

b.钢束张拉控制应力调整后的计算。为减少曲线梁截面底缘内外侧应力差，可通过调整曲线梁底板内外侧钢束张拉控制应力，把部分梁底板外侧的钢束张拉控制应力调整为0.75fpk= 1 395 MPa，内侧的钢束张拉应力调整为0.65fpk=1 209 MPa;通过模拟计算，在运营阶段主+附加力作用下，桥梁跨中底缘正应力见表2。

表2　跨中截面底缘正应力(二)　MPa

从表2的计算结果可以看出，钢束张拉控制应力调整后，曲线内侧的应力略为减小，但不明显;第一、第二跨跨中截面曲线外侧的应力增加比较明显，分别增加了28%和30%，第三跨由于位于直线上，底板的钢束张拉控制应力没有调整，其对应的截面内外侧的应力基本无变化。

6　结语

1)曲线梁桥由于腹板内短外长，在同样的荷载作用效应下，曲线梁桥外侧的腹板受力要比内侧腹板大，截面外侧的应力比内侧的应力要小，并且曲率越小，截面内外侧的应力相差越大。

2)通过调整曲线梁桥底板内外侧的张拉控制应力差，可明显减小曲线梁桥截面内外侧的应力差，使曲线梁桥截面内外侧应力趋于均匀。

3)曲线梁桥由于桥梁结构自身受力的特殊性，相比同等跨径的直线梁桥要复杂，曲线梁桥的受力不可避免地存在“弯—扭”耦合作用，这会引起曲线梁桥截面内外侧应力存在差异，因而要在结构计算和设计中引起足够的重视。本文通过调整内外侧预应力钢束张拉控制应力的方法来优化截面应力，用三维计算软件Midas civil 2012进行模拟计算，并验证了其有效性，可以为同类桥梁的设计提供参考。

参考文献:

［1］TB 10623—2014，城际铁路设计规范［S］.

［2］TB 10002.3—2005，铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.

［3］孙广华.曲线梁桥计算［M］.北京:人民交通出版社，1997.

［4］薛宇光.铁路小半径曲线连续梁桥设计研究［J］.铁道建筑技术，2014( 6) :1-4.

［5］许延祺.顶板短束在城市小半径曲线梁桥中的应用［J］.铁道工程学报，2012( 1) :35-39.

［6］陈光.浅析混凝土弯桥结构设计［J］.北方交通，2014( 6) : 43-45.

［7］王一文，李广慧.曲线连续箱梁桥的受力性能分析［J］.河南科学，2014( 9) :1743-1746.

Stress optimization of the curve continuous T-shaped rigid frame bridge

Fan Qinfeng
( Guangzhou Institute of the China Railway Siyuan Survey＆Design Group Co.，Ltd，Guangzhou 510600，China)

Abstract:This paper takes Xintang station grand bridge of Guangzhou Dongguan Shenzhen intercity railway as the background，using Midas civil 2012 to build space finite element model of the bridge.Simulation calculation is carried out on tension control stress for prestressing of adjustment before and after adjustment，the results show: adjusting the tension control stress of internal and external prestressing tendons of curved girder bridge can significantly reduce the stress difference of the section of curved girder bridge.

Key words:T-shaped rigid frame bridge，curve beam bridge，stress optimization

作者简介:范琴锋(1982-)，男，硕士，工程师

收稿日期:2015-11-24

文章编号:1009-6825( 2016) 04-0176-02

中图分类号:U448.231

文献标识码:A