基于智能优化方法的SVM电机故障诊断模型研究

赵慧敏，房才华，邓武，聂冰(大连交通大学软件学院，辽宁大连116028)*

基于智能优化方法的SVM电机故障诊断模型研究

赵慧敏，房才华，邓武，聂冰
(大连交通大学软件学院，辽宁大连116028)*

为提高电机故障诊断的准确率和有效性，提出了基于智能优化算法的支持向量机电机故障诊断模型.首先采集交流电机不同位置上的振动加速度信号，使用小波包分析方法对所采集的振动加速度信号进行特征提取，将得到的能量比向量作为支持向量机故障诊断模型的输入，使用遗传算法、粒子群优化算法对支持向量机故障诊断模型进行参数优化并进行模型训练，在使用测试样本集对得到的两种故障诊断模型进行分析之后可以看出经过参数优化后的支持向量机模型提高了故障预测的准确率，并且粒子群优化方法具有比遗传算法更高的预测准确率，并极大地减小了优化时间及优化次数.

支持向量机;粒子群优化算法;遗传算法;电机故障诊断

0 引言

随着现代测试技术、信号处理技术、人工智能技术、特别是知识工程、专家系统等的飞速发展，电机故障诊断技术取得了很大的进展，出现了以模糊推理［1］、神经网络［2］、灰色预测［3］、遗传算法［4］、小波分析［5］、支持向量机( Support Vector Machine，SVM)［6］等为基础的智能故障诊断技术.在这些方法中，支持向量机因其在解决小样本、非线性问题上的优越性，近年来在故障诊断领域得到了较为广泛的应用.但在实际应用中发现，支持向量机模型参数的选择会对分类的效果有很大影响.例如，文献［7］运用支持向量机方法进行故障诊断，由于未使用参数优化，得到的分类器效果并不能达到理想的效果.文献［8］提出了基于局部切空间排列和支持向量机的电机故障诊断模型，虽然诊断精度高，但是利用网格寻优需要遍历所有的点，耗时相对较长.文献［9］比较了遗传算法与粒子群优化算法的优化效率，但是并未和实际优化问题相结合，并未验证其在实际应用中的广泛性和健壮性.文献［10］利用了梯度下降法优化参数，取得了良好效果，但是梯度下降法容易陷入局部极小值.本文针对交流电机故障诊断问题，讨论了基于支持向量机的故障诊断方法，并针对支持向量机的模型参数优化问题进行研究.

1 基础理论

1.1支持向量机

支持向量机［11］方法根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误的识别任意样本的能力)之间寻求最佳折中，以求获得最好的推广能力.

设线性可分样本集:

( x1，y1)，( x2，y2)，…

其中: xi∈Rd为输入向量，y∈［－1，1］为相应的目标输出.

d维线性空间中分类线对所有样本( xn，yn)分类正确等价于:

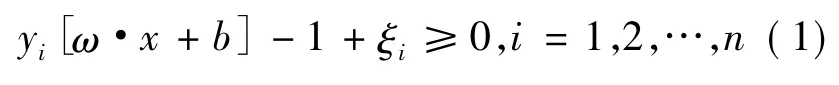
满足等号的样本因为支撑了最优分类面而被称作支持向量.最优分类面的求解可以表示成求如下函数:

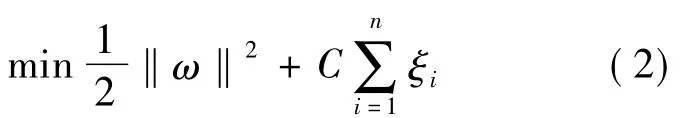
式中:ξi是松弛项，C是惩罚因子，用于控制目标函数中两项之间的权重.ω=α1x1y1+ a2x2y2+…+ anxnyn，其中ai为拉格朗日乘子，可将对式( 2)的求解转化为求对偶问题的最大值

求解式( 3)后所得最优分类函数为

为了简化高维空间中求取最优分类面的运算，使用核函数K( xi，xj)代替最优分类面中的点积.目前使用较为广泛的核函数有线性核函数、多项式核函数、Sigmoid核函数和RBF核函数.基于RBF核函数具有能够逼近任意非线性函数的特性，本文采用RBF核函数作为支持向量机的核函数.RBF核函数为

支持向量机结构示意图如图1所示:

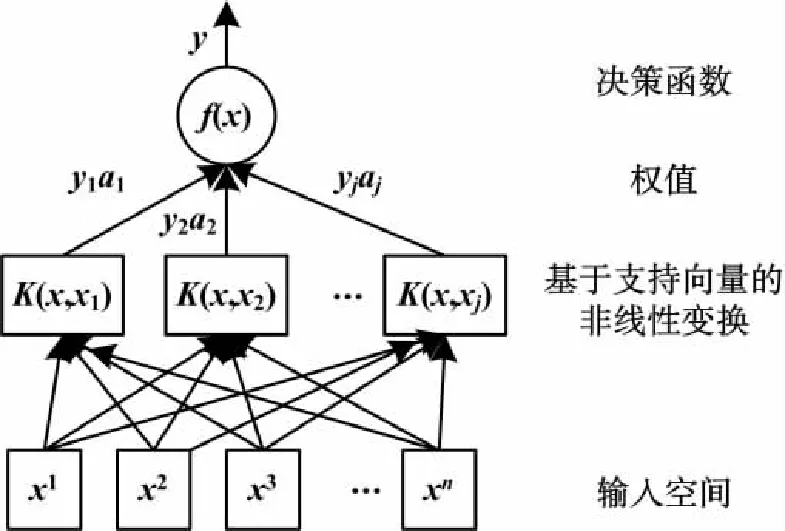
图1 支持向量机结构示意图

1.2遗传算法

遗传算法［12］( Genetic Algorithm，简称GA)是模仿生物进化过程发展而来的全局搜索与优化算法.其基本思路是:根据待寻优问题的目标函数，构造一个适应度函数，然后生成初始种群，对种群进行评价、交叉、变异、选择等操作.通过数次进化，得到适应度最高的个体作为问题的最优解.基本遗传算法的流程图如图2所示.

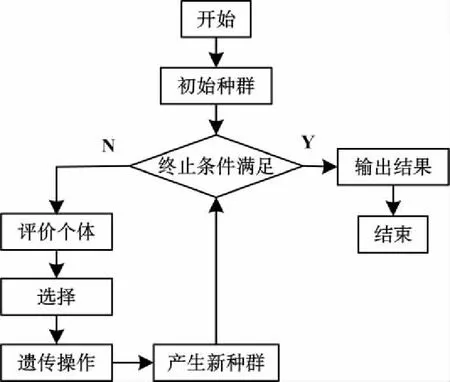
图2 遗传算法流程图

由图2可知，实现GA算法的基本要素主要有:编码操作、适应度函数选取、遗传操作及参数运行.染色体的编码方法有二进制法、实数法等.适应度函数是指进化过程中衡量个体适应度值的函数，应根据适应度函数计算每个个体的适应值然后提供给选择算子进行选择.遗传操作包括选择、交叉和变异操作.参数运行的过程主要包括GA算法在初始化时选取的参数，例如种群大小M、遗传代数G、交叉概率Pc和变异概率Pm.

1.3粒子群算法

1995年，Eberhart和kennedy受鸟群捕食行为的启发，提出了粒子群优化算法［13］.其更新公式为:

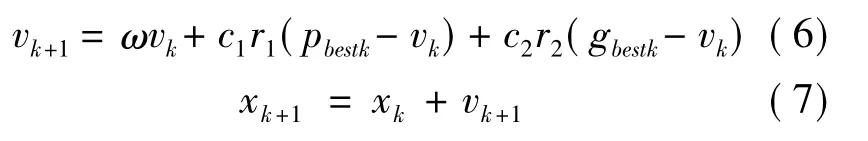
上式中，c1和c2是非负常数的学习因子，通常取c1= c2= 2;ω表示惯性权重，通常其取值在［0，1］之间.

PSO算法基本流程图如图3所示:

图3 PSO基本流程图

2 基于支持向量机的电机故障诊断模型

2.1实验数据采集

本实验所采集的数据是基于变频器驱动的交流电机调速系统实验平台的.振动信号的采集是通过在电机—发电机组的不同部位安放加速度传感器，传感器与NI公司生产的四通道的NI9234相连，将振动加速度数据传递至上位机进行数据的存储.加速度传感器在电机上的安放位置如下:通道Channel 1、Channel 2、Channel 3所对应的位置分别是轴向、电机轴径向水平方向、电机轴径向垂直方向.A/D数据采样频率为12.8 kHz，交流电机的参数为:额定功率为1.5 kW，额定电压为380 V，额定电流为3.4 A，频率为50 Hz，额定转速为2 845 r/ min.数据采集的步骤如下:

( 1)交流电机稳定在某一转速下，采集n组交流电机振动加速度数据并对获得的数据进行消噪处理;

( 2)采用小波包分析方法对振动加速度数据进行分解，得到各个子频带的能量比值，采用三层分解的方式进行分解，分解之后得到8个频率由低到高的正交子频带的能量比分量，构成n组8维的能量比向量［14］.

分别采集交流电机三种状态下的振动加速度数据，用以模拟三种故障状态.本次试验共获取了48组数据，分别为:第一种状态为22组，第二种状态为16组，第三种状态为10组.对每组数据的轴向、电机轴径向水平方向、电机轴径向垂直方向的振动加速度数据分别进行三层能量比分解，每个方向获得8个能量比，每组共计24个特征属性.这里选取3种状态各8组数据总共24组数据作为训练样本，剩余24组数据作为测试样本.

2.2故障诊断模型

本文针对交流电机的故障诊断问题，采用基于支持向量机的故障诊断模型.本文所采用方法的具体流程主要包括以下步骤.

( 1)将n组能量比向量数据中的前n/2组作为训练样本集，后n/2组作为测试样本集;

( 2)使用遗传算法、粒子群优化算法分别对SVM模型进行参数优化，并进行SVM模型参数训练，当训练后的交叉准确率达到90%以上即可认为训练完成;

( 3)训练结束后再将训练好的支持向量机模型对测试样本集进行测试，将得到分类准确率和测试的标签，若结果达到要求便可以将此模型用于交流电机的故障诊断.

3 电机故障诊断模型的参数优化方法研究

在实际应用中，发现支持向量机模型参数的选择会对分类精度有较大的影响，即在训练与测试样本相同的情况下，在模型参数不同时所得到的预测正确率并不相同，其中影响较大的是惩罚因子C与核函数的参数g.因此如果得到最佳的C 和g，即获取了具有最佳分类性能的支持向量机模型，因此本文接下来讨论使用遗传算法和主粒子群优化方法对基于支持向量机的电机故障诊断模型进行参数优化的过程并对实验结果进行了分析.

3.1基于遗传算法的模型参数优化方法

本节采用1.2节所介绍的遗传算法对基于支持向量机的电机故障诊断模型的参数C和g进行优化.

参数优化的步骤为:

( 1)初始化:生成第一代种群，种群规模大小为20、交叉概率Pc为0.9、变异概率Pm为0.01、最大迭代次数T_max为100次，对SVM中的惩罚因子C与核函数的参数g进行二进制编码;

( 3)选择、交叉、变异;

( 4)生成新一代种群，判断是否达到误差要求或达到最大迭代次数，若是，转到( 5) ;否则转到( 3) ;

( 5)获得惩罚因子C与核函数的参数g的最佳组合;

( 6)获得参数优化后的SVM模型.

将以上的参数优化算法在matlab中运行，可以得到粒子适应度随进化代数的变化如图4所示.整个参数寻优过程的运行时间为13.196 s，寻优之后的最佳参数C = 22.243 1，g = 2.141 59.由于样本训练量较小，所以参数寻优过程较快.将此优化的参数对训练集样本进行SVM模型训练，训练完成后对测试集数据进行测试，测试结果为第18，20，24组数据分类错误，其余21组分类正确，测试正确率为Accuracy = 87.5% ( 21/24).

图4 遗传算法优化与粒子群算法适应度曲线

3.2基于粒子群算法的模型参数优化方法

本节采用1.3节所介绍的粒子群算法对基于支持向量机的电机故障诊断模型进行参数优化.

参数优化的步骤为:

( 1)初始化:种群规模大小为20、c1= 1.5、c2= 1.7、ω初始值为0.6、最大迭代次数T _max为30次;

( 2)计算适应度值，适应度函数为: P( C，g) =，P( C，g)是在参数C，g下的分类识别率，R( C，g)是正确识别的个数，R( C，g) + W( C，g)是支持向量机能够识别的总样本个数;

( 3)计算个体历史最优位置与群体历史最优位置，跟踪新粒子的位置与速度;

( 4)生成新一代种群，判断是否达到误差要求或达到最大迭代次数，若是，转到( 5) ;否则转到( 2) ;

( 5)获得惩罚因子C与核函数的参数g的最佳组合;

( 6)获得参数优化后的SVM模型.

将以上的参数优化算法在matlab中实验多次，当最大迭代次数为30时，此时得到的参数优化效果已经非常理想，得到粒子适应度随进化代数的变化曲线如图5所示.整个参数寻优过程的运行时间为2.091 s，寻优之后的最佳参数C = 0. 1，g = 0.1.将此优化的参数对训练集样本进行SVM训练，训练完成后对测试集数据进行测试，测试结果为第23组数据分类错误，其余23组分类正确，测试正确率为95.8333% ( 23/24).在遗传算法中染色体互相共享信息，而粒子群算法中只有gbest将信息共享给其他粒子，这使得更新过程跟随当前最优解，搜索性能上好于遗传算法.

3.3实验比较分析

表1中列出了未进行参数优化与进行遗传算法优化、粒子群优化之后进行SVM训练和测试的相关结果.

表1 实验结果比较

从表中我们可以得到如下结论:

( 1)对比支持向量机进行参数优化前后的测试准确率，我们发现支持向量机在进行参数优化后的测试准确率得到了大幅度的提高.并且整个学习过程不需要人工干扰，大大提高了模式识别的自动化程度和精度;

( 2)对比遗传算法与粒子群算法的迭代次数(进化代数)与运行时间可以发现，遗传算法找到最优解的迭代次数高于粒子群算法而且优化时间较长.这是因为粒子群优化算法没有遗传操作，如交叉和变异，算法复杂度更低，随机性更强.比遗传算法更快收敛于最优解，运行效率上大大优于遗传算法.

4 结论

本文针对交流电机故障诊断中，故障诊断模型结构难于选择、欠训练，存在极小值等问题，采用了基于小波包、智能优化算法和支持向量机的故障诊断模型，利用小波包方法具有多分辨率分析的特点对采集的振动数据进行了特征提取，探索了使用遗传算法、粒子群算法对SVM模型进行参数优化的有效性，并通过实验分析粒子群参数优化方法较之遗传算法的优势，即它不仅具有优化时间短的特点，且使得到的支持向量机故障诊断模型的故障测试精度更高.

［1］GIAP QUANG HUY，PLOIX STEPHANE，ADROT OLIVIER，et al.ChristianInteractive diagnosis for a grid network of rain gauges using fuzzy reasoning［J］.Engineering Applications of Artificial Intelligence，2014，36: 99-113.

［2］SARAVANAN N，SIDDABATTUNI，KUMAR V N S，et al.Fault diagnosis of spur bevel gear box using artificial neural network ( ANN)，and proximal support vector machine ( PSVM)［J］.Applied Soft Computing Journal，2010，10( 1) : 344-360.

［3］WANG M H.TSAI H H.Fuel cell fault forecasting system using grey and extension theories［J］.IET Renewable Power Generation，2012，6( 6) : 373-380.

［4］NGUYEN N-T，LEE H-H.Improvement of induction motor fault diagnosis performance by using genetic algorithm －based feature selection［J］.Proceedings of the Institution of Mechanical Engineers，Part C: Journal of Mechanical Engineering Science，2008，222( 8) : 1613-1619.

［5］WU JIAN-DA，LIU CHIU-HONG.An expert system for fault diagnosis in internal combustion engines using wavelet packet transform and neural network［J］.Expert Systems with Applications，2009，36( 3) : 4278-4286.

［6］WIDODO ACHMAD，KIM ERIC Y，SON JONG-DUK，et al.Fault diagnosis of low speed bearing based on relevance vector machine and support vector machine［J］.Expert Systems with Applications，2009，36 ( 3) : 7252-7261.

［7］陈兴辉.基于小波与支持向量机的滚动轴承故障诊断［D］.太原:太原理工大学，2006.

［8］万鹏，王红军，徐小力.局部切空间排列和支持向量机的故障诊断模型［J］.仪器仪表学报，2012( 12) :2789-2795.

［9］任斌，丰镇平.改进遗传算法与粒子群优化算法及其对比分析［J］.南京师范大学学报(工程技术版)，2002 ( 2) : 14-20.

［10］OLIVIER CHAPELLE，VLADIMIR VAPNIK，OLIVIER BOUSQUET，et al.Choosing Multiple Parameters for Support Vector Machines［J］.Machine Leaning，2002，( 46) : 131-159.

［11］VAPNIK V N.The Nature of Statistical Learning Theory ［M］.Germany: Springer，2000.

［12］JUDSON R S，JAEGER E P，TREASURYWALA A M，et al.Conformational searching methods for small molecules.II.genetic algorithm approach［J］.Journal of Computational Chemistry，1993，14( 11) : 1407-1414.

［13］KENNEDY J，EBERHART R C，SHI Y.Swarm intelligence［M］.San Francisco: Morgan Kaufmann Publishers，2001.

［14］赵慧敏，房才华，徐智超，等.一种交流电机故障诊断中的特征提取与强化［J］.大连交通大学学报，2014 ( 2) : 93-97.

［15］王雪梅，王义和.模拟退火算法和遗传算法的结合［J］.计算机学报，1997，20( 4) : 381-384.

Research on Motor Fault Diagnosis Model for Support Vector Machine based on Intelligent Optimization Methods

ZHAO Huimin，FANG Caihua，DENG Wu，NIE Bing
( Software Institute，Dalian Jiaotong University，Dalian 116028，China)

In order to improve the accuracy and efficiency of motor fault diagnosis，a new method of support vector machine was proposed based on intelligent optimization algorithms.After collecting AC motor vibration acceleration signals at different positions，the feature extraction with wavelet packet analysis method was conducted，and power ratio of the result of feature extraction were used as the input to the motor fault diagnosis model for support vector machine.The genetic algorithm and the particle swarm optimization algorithm can be used for parameter optimization and model training of the motor fault diagnosis model for the support vector machine.Fault diagnosis model analysis shows that after parameter optimization，the fault diagnosis model improves the forecasting accuracy，and the particle swarm optimization algorithm has higher prediction accuracy than the genetic algorithm with greatly reduced time and times of optimization.

support vector machine; particle swarm optimization algorithm; genetic algorithm; motor fault diagnosis

A

1673-9590( 2016) 01-0092-05

2015-05-13

国家自然科学基金资助项目( 51475065) ;人工智能四川省重点实验室基金资助项目( 2014RYJ01) ;过程装备与控制工程四川省高校重点实验室开放基金资助项目( 2014RYJ01)

赵慧敏( 1977－)，女，副教授，博士，主要从事分数阶控制电机故障诊断的研究

E-mail: hm_zhao1977@126.com.