让学生的思维看得见——特级教师顾娟《和的奇偶性》片断赏析

顾银燕

《和的奇偶性》是苏教版五年级下册新增的内容，是在学生学习了《倍数和因数》单元后安排的一次探索规律的活动。既是规律教学课，大抵是按经历猜想——通过举例——进行验证——归纳总结的数学活动过程，从而得出数学规律。然而这样的规律教学课，也因为套路明显，上不出新意，让笔者颇为困扰。前几天聆听了特级教师顾娟执教的《和的奇偶性》，让我如醍醐灌顶，茅塞顿开。原来，有套路的课还可以上得这样不落入俗套！现截取片断，与同行分享。

【片断一】

师：同学们喜欢看电视吗？江苏卫视播过一档很火的节目——《最强大脑》，有没有看过？我们一起看一段！（播放第二季第二场“铁脑三项”的比赛片断）

师：中国小选手好厉害啊！如果现在让你们去跟他比，敢不敢挑战？

生：（摇头）不敢，他们算得太快了！

师：不敢是正常的，毕竟我们没有经过专业的训练。不过，在今天的数学课上，也有一些挑战性的问题，你敢不敢挑战？看谁是我们班的最强大脑，好吗?

生：好!

(出示转盘，教师宣读游戏规则）

师：抽出的数再加一次是什么意思？

生：比如抛中3，就是3+3=6，那就是点开 6，看后面有没有奖品。

（请3名同学分别上来抛骰子，分别抛中 6、3、4）

生：老师，我觉得不用再抛了，根据我的猜测，双数一定是“谢谢参与”，而无论你抛中骰子上的哪个数，再和这个数本身加一次，结果一定是双数。

（全场开始有几个人小声附和，继而附和的人多了起来）

师：（疑惑地）咦？抛中骰子上一个数，再追加一次一定是双数吗？

生：一定！1+1=2、2+2=4、3+3=6、4+4=8、5+5=10、6+6=12。

师：我们点开转盘看看奖品的设置，好不好？

（打开后，双数点全部是“谢谢参与”）

师：既然是这样，肯定不会抽到奖，想修改游戏规则吗？

生：把转盘依次转一格，这样不管你抛到几，都有奖！（全班大笑）

生：这样太没意思了！我可以抛两次，把两次抛中的数加起来，这样有可能中奖。

师：（追问）这位同学的想法挺有意思的！我想采访一下你，根据数的奇偶性，可能抛到什么结果？

（学生回答后，教师板书：奇+偶=奇 奇+奇=偶偶+偶=偶）

【赏析：陈鹤琴先生曾指出：“游戏是人生不可缺少的活动，不管年龄性别，人们总是喜欢游戏的。假如在读书的时代，我们也能化读书的活动为游戏，那么读书不是会变得更有趣，更快乐，更有进步了吗？”因此，游戏在教学中的作用不可小觑，合适的游戏是启发心智与兴趣，达到身心愉悦的最佳方式。“和的奇偶性”这个知识比较抽象，离学生生活较远，如果单刀直入式地开展教学，则无法引起学生浓厚的兴趣，从而无法激发学生探究的欲望。顾娟老师在课的开始，采用抛骰子中奖品这一游戏方式，抓住学生的兴趣，让学生的思维一下子被点燃，同时利用学生生活中参与游戏抽奖的经验，让学生思考“为什么屡屡不中奖？”从而对游戏规则产生质疑，继而发现和的“秘密”，即两个相同的数相加得偶数。这样的设计妙在问题从学生身边来，能引起学生关注的热情。顾娟老师又巧妙地用“修改游戏规则”这个环节，让学生对两数之和的奇偶性引发进一步的思考与探究，从而将问题从特殊引向一般，从个例导向共性。剖开游戏的外衣，学生思维由点引向面、由肤浅引向深刻。】

【片断二】

师：我们在玩游戏中研究数学学问，真好！任意两个自然数相加是不是都有这样的规律呢？怎样验证？

生：我们可以举例。（教师点名几个学生回答）

师：这样的例子举得完吗？如果有一个例子不符合刚才的规律，我们又恰好没发现，怎么办？除了举例，还可以怎样验证呢？

（学生冥思）

出示华罗庚的一段话：数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。

生：（恍然大悟）画图！

出 示 ：像 249+119、127+116、3026+2874 你能不计算，判断出和是奇数还是偶数吗？

【赏析：对和的奇偶性规律的认识，学生之前还仅仅是建立在单双数的基础上，通过举例不完全归纳得出结论。这样的认识显然是不深刻、不全面的。如何让学生对这部分知识建立起科学、完整、深刻的认识，顾娟老师的设计又出亮招。出示华罗庚关于数形结合的一段话，为学生打开另一扇窗，利用画图来表征偶数+偶数=偶数，偶数+奇数=奇数，奇数+奇数=偶数，将抽象的知识直观表达，借助图形运用演绎推理，验证规律的正确性。】

【片断三】

师：刚才我们研究了两数之和的奇偶性，想想根据这个我们还可以推出什么规律？

生：三个数和的奇偶性。

生：还可以是更多数和的奇偶性。

板书：

师：如果是m个偶数相加的和，n个奇数相加的和，结果是怎样的？

生：不管是多少个偶数相加，结果都是偶数，奇数就要看具体情况了，如果n是偶数，那么和是偶数，如果n是奇数，那么和是奇数。

师：m个偶数相加，结果是偶数。n个奇数相加，能具体解释解释吗？

生：如果n是偶数，两个奇数配成一组，这样也就没有剩余，和是偶数；如果n是奇数，两两配对还多一个，那和就是奇数了。

（学生自发响起热烈的掌声）

接着师板书：

师：如果是这种情况呢？（在m个偶数相加和n个奇数相加的算式中加一个“+”）

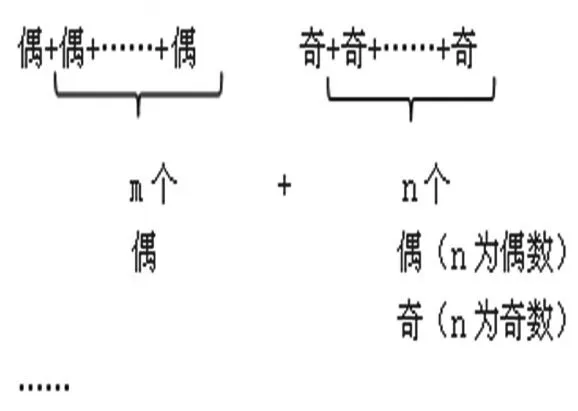
师：大家还记得开始看的《最强大脑》吗？你们想挑战一下吗？

教师陈述规则：每次屏幕上只出现一个加数，最后一个加数报完，立刻说出和是奇数还是偶数。

246+199+1023+2048+1357+731

生：偶数！

师：好多数相加，和的奇偶性跟什么有关？

【赏析：由两个数和的奇偶性拓展到更多数的和的奇偶性，这是学生知识树不断生长与丰满枝叶的过程。顾娟老师智慧地抛出问题“m个偶数相加与n个奇数相加的结果是什么数？”学生通过原来的经验，借助于“偶+偶=偶，奇+偶=奇，奇+奇=偶”以及图像表征的经验，再次进行演绎推理，让这三个式子的规律得到延展与提升。在这一过程中，教师没有过多地帮扶，更多的时候是一个倾听者与提问者，在学生思维容易混沌的地方，适时地打住：“能具体解释解释吗？”“如果是m个偶数与n个奇数相加呢？”“好多个数相加，和的奇偶性跟什么有关？”通过一个个重要的问题引导学生理清思维，从复杂的问题中抽丝剥茧，把握规律的本质。】