寻求有效策略理清易混概念

孙保华

一、聚焦：形成概念混淆的原因

数学概念是反映客观事物在数量关系和空间形式方面的本质属性的思维形式。由于客观事物在数量关系和空间形式方面存在着联系和区别，所以某些概念在表述形式或内涵、外延方面也存在着一定的联系和区别。另外小学生的概括、推理和理解等能力还处于初级水平，生活经验也不够丰富，所以在学习某些概念时，容易发生混淆。主要表现在以下几个方面：

1援由概念的交叉关系引起的混淆。

如果在两个概念中，每个概念的外延都只有一部分元素属于另一个概念的外延，那么这两个概念之间就具有交叉的关系。奇数和质数、偶数和合数均属于交叉关系的概念，它们的外延仅有一部分是互相重合的。但由于大部分的质数都是奇数，大部分的偶数都是合数，在教学中我们如果不注意加以引导，学生就很容易错误地把“奇数”当作“质数”，把“偶数”当作“合数”，从而将这两组不同类的概念混淆起来。

2.由概念的属种关系引起的混淆。

在小学数学教材中，有许多属于属种关系的概念，大概念里面包含着小概念。大、小概念之间既联系紧密，又区别明显，大概念反映的是共性，小概念反映的是特性。可是，有些学生只看到明显区别的不同点，把本是属种关系的两个概念所反映的对象看作是对立关系，把这两个概念对立起来。例如，正方形是特殊的长方形，由于在低年级初步建立这两个概念时，没有了解它们之间的关系，所以到了高年级学习长方体和正方体时，也错误地把它们对立起来，看不透一般与特殊的关系。

3.由概念共同的词素引起的混淆。

在一个概念的前面冠以一个词或词素来修饰，就可以使原概念的内涵得到加深，从而形成一个新的概念。例如，“质数”和“互质数”是完全不同的两个概念。一个数只有1和它本身两个因数，这样的数叫做质数；公因数只有1的两个数，叫做互质数。有的学生只从概念本身的文字看，以为“互质数”是“质数”前面添了一个“互”字（其实是“互质”后面添了一个“数”字），所以片面地理解为互质的两个数都应是质数，把互质数和质数混淆起来，不恰当地缩小了互质数的外延。

4.由概念分类不当引起的混淆。

分类可以进一步理清概念之间的联系，从而能有条理、系统地掌握这些概念。但概念的分类也有一定的规则。譬如，每次分类只能根据一个标准，子项必须互相排斥，分类不能越级。但由于学生不具备这方面的知识，有的教师又没有去积极引导，结果造成了概念上的混乱。例如，有的学生将小数划分为有限小数、无限小数、循环小数。这里前两种是根据小数的位数来划分的，而循环小数属于无限小数的一种。不按照同一标准来划分，就有可能造成重复和遗漏。

二、寻求：理清概念的有效策略

在教学容易混淆的概念时，除了要直观形象地引进概念，抓住本质属性去讲清概念以外，还应通过下面各种策略来帮助学生掌握概念之间的联系与区别，使概念不断得到巩固和深化。

1.易混概念对比策略。

随着学习的深入，学生掌握的概念不断增多，有些概念的文字表述相同，有些概念内涵相近，使得学生容易产生混淆，如位数与数位，体积与容积等。因此要注意组织学生运用对比的方法，弄清易混概念的区别和联系，以促使概念的精确分化。例如将求比值和化简比进行对比如下：

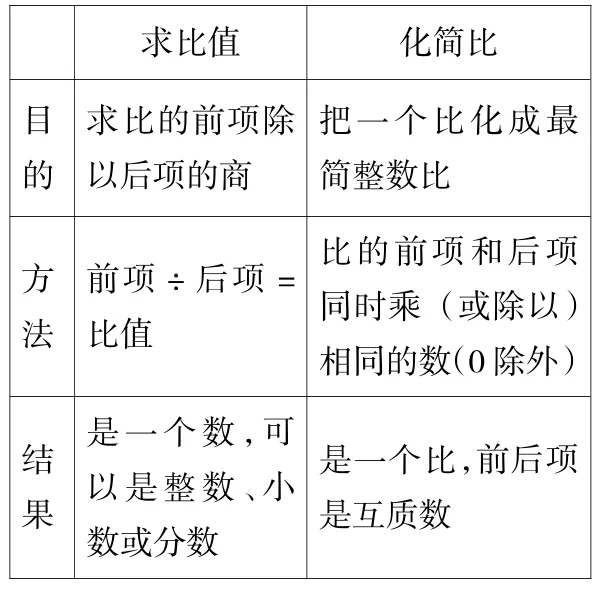
求比值 化简比目的求比的前项除以后项的商把一个比化成最简整数比方法比的前项和后项同时乘（或除以）相同的数（0除外）前项÷后项=比值结果是一个数，可以是整数、小数或分数是一个比，前后项是互质数

2.运用变式辨析策略。

概念的肯定事例传递了有利于概括的信息，否定事例传递了有利于辨别的信息。因此教学中要充分运用肯定事例来强化学生对概念内涵的理解，同时要及时运用否定事例来促进学生对概念的辨析，进一步促进学生对概念本质属性的深刻理解。

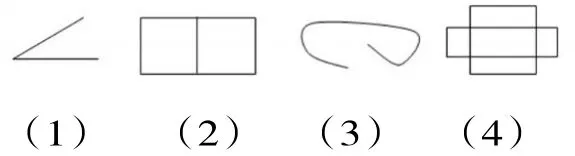
例如，在教学《认识周长》一课时，学生通过肯定事例建立了周长的概念，但没有深入去剖析周长的本质属性，教师适时抛出下面的四个图形，让学生分别指出这些图形的周长。学生可能出现两种情况：一种是束手无策，不知道从何下手；一种是把所有的线都指一遍。此时，教师就问：“为什么你找不到图（1）和图（3）的周长呢？图（2）和图（4）的周长到底指哪部分？”通过学生的讨论、分析、辩论，学生能够明确图（1）和图（3）两个图形不是封闭图形，所以没有周长；而图（2）和图（4）的周长应该指的是这两个图形外面一圈线段的总长，与图形内部的线段没有关系。这里通过正、反两种方式进行对比、变式教学，学生对周长概念的理解由模糊到清晰，对周长的认识由感性认识上升到理性认识，明确周长这一概念的本质就是封闭图形一周的长度。

3.概念结构图解策略。

所谓概念结构图解策略就是用一个结构图把相关联而又分散的知识系统化、条理化，从而形成知识网络的一种学习策略。形象地说就是根据知识之间整体与部分之间的关系、知识之间的内在规律与联系，搭设知识“骨架”，从而掌握“知识的全貌”。同时，系统化、结构化的知识更有利于学生的理解和保持，因此当学生学习了一定数量的概念后，教师就要帮助学生形成正确的概念系统。为此，教学中常用如下方法：

（1）用分类的方法表示概念外延间的关系。通过分类可以揭示概念的外延，使知识条理化、系统化，防止概念的混淆。如三角形以角为标准，可分类为：

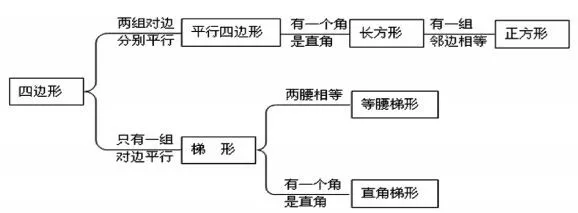
（2）用增加内涵的方法表示概念内涵间的关系。随着概念内涵的增加，外延将缩小。据此，可以把概念整理成系统。如几种四边形内涵间的关系可用下图来表示。

（3）用集合图表示概念外延间的关系。在揭示某些概念之间的关系时，可以用集合图。几种三角形外延间的关系可用下图来表示。

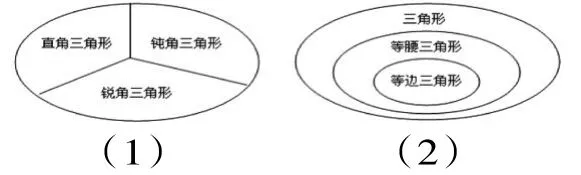
由图（1）可以直观地看到，在三角形中，直角三角形、锐角三角形和钝角三角形是并列的概念，它们的外延没有交叉。由图（2）可以直观地看到三角形、等腰三角形、等边三角形都是属种关系，后一概念的外延包含于前一概念的外延之中。

4.灵活应用概念策略。

在概念教学中，既要引导学生由具体到抽象，形成概念，又要让学生由抽象到具体，运用概念。学生是否牢固地掌握了某个概念，不仅在于能否说出这个概念的名称和背诵概念的定义，而且还在于能否正确灵活地应用，通过应用可以加深理解，提高数学应用的意识。概念的应用可以从概念的内涵和外延两方面进行。

总之，在学生建立了正确的概念后，要运用各种有效策略，帮助学生理清概念，从而深化概念的理解和巩固，使学生更清楚地认识知识的内在联系,促进学生认知结构的完善和发展，同时为学生灵活运用概念做铺垫，培养学生的思维能力。