三维人体测量精度的比较分析

王蓉、张文利、赵蒙蒙、李艳梅,上海工程技术大学服装学院

近几年随着社会的发展,消费者在追求服装时尚的同时还要有个性，符合自身的需求。而且我国是人口大国，不同民族和地区的人体特征差异较明显，因此现行的国家号型标准体系已经不能很好地适应大批量的服装生产，同时也不能满足服装定制的需求。为了获得精准的人体特征原始数据，准确的制定我国的服装号型规格以及满足消费者个性化的需求，这就对人体测量方式提出了更高的要求。在人体测量的发展过程中，由接触式的测量过渡到非接触式的测量，由二维向三维发展，同时包含自动测量以及计算机的测量数据的处理和分析。现在比较常用的人体测量方式有手工测量和三维扫描测量，传统的手工测量更加方便直观，而三维扫描测量则有准确高效的优点。对此，本文进行了两种测量方式的对比研究，探索不同测量方式所得数据的相互转换方式。

1 试验方案

1.1 试验对象

全国人体测量上海地区数据库中抽取男性200人，年龄为17～60岁，平均年龄35.3岁，平均身高168.95 cm。水平前伸；左臂屈肘呈90°；两手腕水平。同时左手大拇指分开；右手五指并拢。座椅高度适中，使脚接触地面；腘窝处轻触椅面；大腿和小腿呈90°；从正面看，两肩同高度，眼睛目视前方，双腿并拢。

图3 三维全身扫描姿势—坐姿

（3）标记点的描画和张贴要求

每个被测人身上需黏贴18个标记点，见表2。

表2 三维扫描测量黏贴的18个点的位置

1.3 试验方法

采用手工测量及三维扫描人体测量对着紧身内衣裤的测量者进行测量。

手工测量由经过相关培训的试验人员使用马丁测量仪的工具对被测者进行测量，首先用标记带将需要测量的部位标记一下，然后进行手工测量。测量时要求被测者直立站立，尽可能不要晃动，在测量期间保持姿势，以确保获取较为精确的数据。

图1 各年龄段人数统计

如图1所示，其中17～30岁的人有97人，31～40岁的有77人，50岁以上的为26人，从左到右呈现递减的趋势，对应的，所占的百分比从17岁到60岁呈现递减的趋势，说明参与测量的200人中青年的人数较多为86%，老年人约占13%。

1.2 测量仪器与要求

1.3.1 测量设备及精度要求

手工测量以及三维扫描测量使用的设备及精度要求见表1。

表1 测量设备及精度要求

三维人体扫描仪测量要求

（1）立姿

自然站立，分两个姿势，立姿I如图2左，两手臂和躯干分开的角度要大一些，尤其是体型比较胖的人；立姿II如图2右，自然站立，两手臂自然下垂，贴近身体。

图2 三维全身扫描姿势-站姿

（2）坐姿

坐姿要求被测者挺胸坐在升降测试椅上，保持三个90°，如图3所示。从侧面看，右臂

测量时，将手工测量的部位上的标记带换成能够被三维扫描仪扫描到的标记点再进行测量，要求被测者严格按照仪器测量要求站立，身体尽量不晃动，保持平衡，以减少由于人体晃动带来的随机误差的影响，获取较为精确的测量数据。

1.3.1 人体测量部位

手工测量和三维扫描测量的部位对比，见表3。

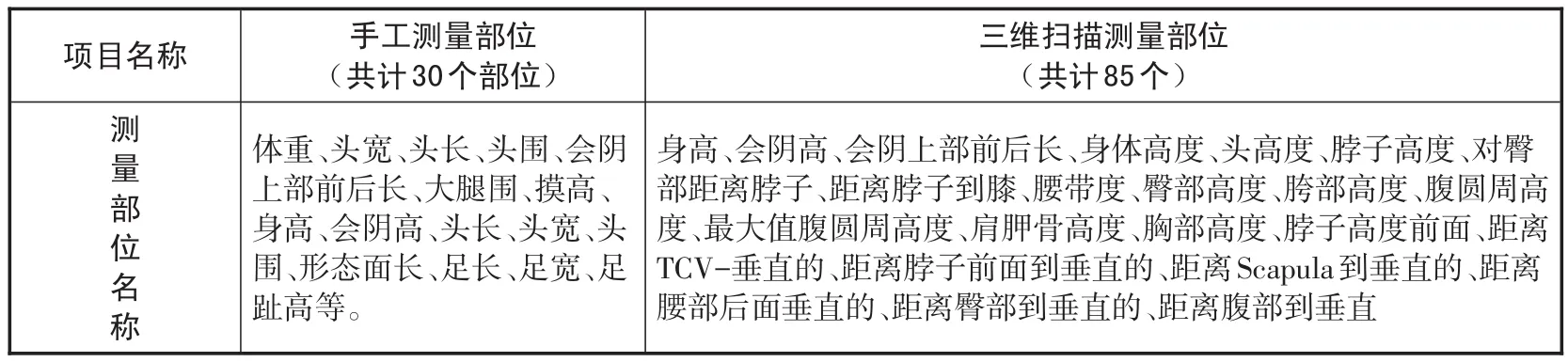
表3 手工测量部位与三维扫描测量部位

选取的手工和三维测量交叉的测量部位，见表4。

表4 手工和三维测量交叉的测量部位及测量方法

1.3.2 对测量者和被测量者的要求

（1）被测人着装要求：

①被测人必须佩戴统一的测量帽，将所有头发置于测量帽内。

②男性着装：赤足，仅着紧身浅色不带花边的三角内裤，内裤无明显褶皱，裤腰不超过脐点。

（2）测量者的要求：

传统的人体测量需要测量者有专业的测量知识，清楚地掌握人体的各个基准点及其位置，测量的项目、方法。

2 数据的处理及分析

2.1 数据提取

对于测量的所有人体数据并不能直接用于数据的分析，要先对测量的人体数据进行分类和提取。

（1）手工测量数据的选取

从30个手工测量的数据里提取出需要的数据：会阴上部前后长、上臂围、大腿围、身高、会阴高体重，表5列出了部分数据示例。

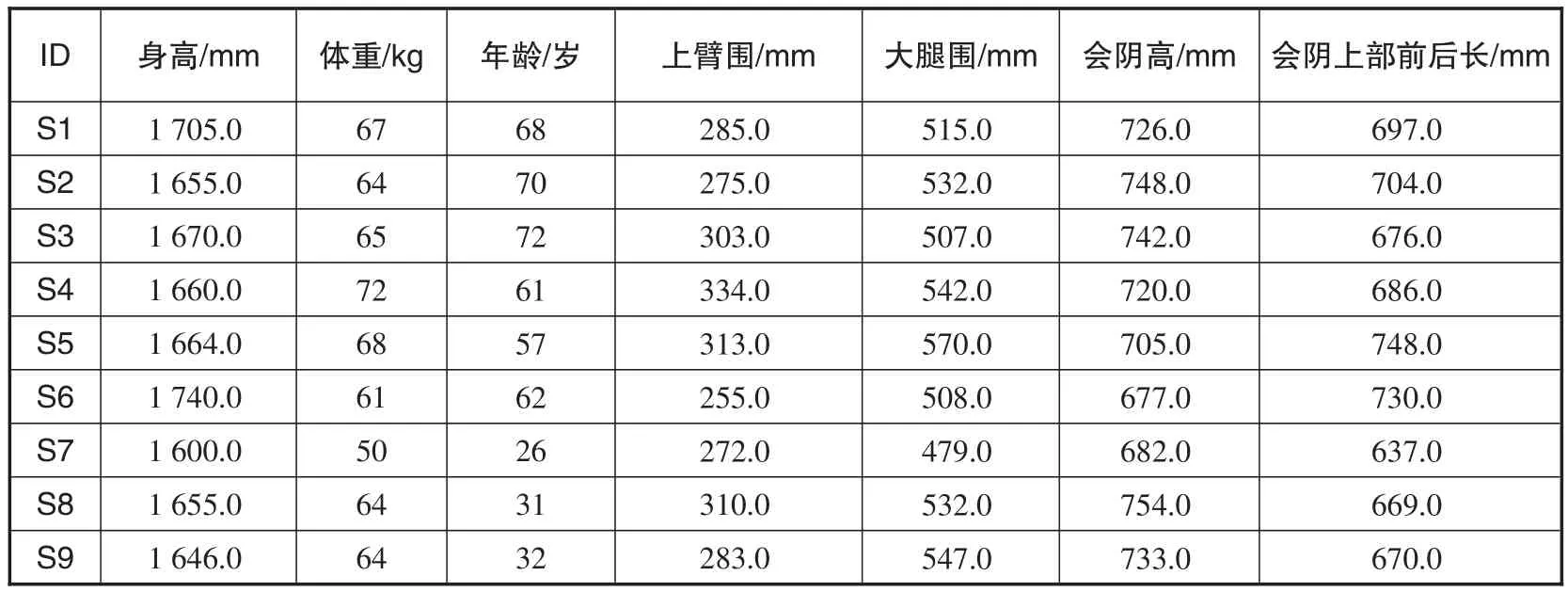
表5 手工测量数据整理

（2）三维扫描测量数据的选取

三维扫描人体测量时，由于有遮挡现象，部分区域没有原始数据，因此要筛选出有效数据，而且原始数据的格式不能直接利用，需要对数据的类型进行转换，以便于分析。对数据进行筛选之后整理，表6列出了对应的部分数据示例。

表6 手工测量数据整理

2.2 数据分析

通过相关分析找到三维扫描人体数据与手工测量数据之间的关联性，对比两种测量方法测得人体数据的差异性，为二者之间的转换找到通路。因测量部位众多，着重以身高为例阐述分析方法，其他部位的研究思路相同，后面将给出对应的分析结果。

2.2.1 身高的显著性差异检验

（1）通过P-P概率图来检验仪器测量（图4～b）和手工测量数据（图4-a）的分布。

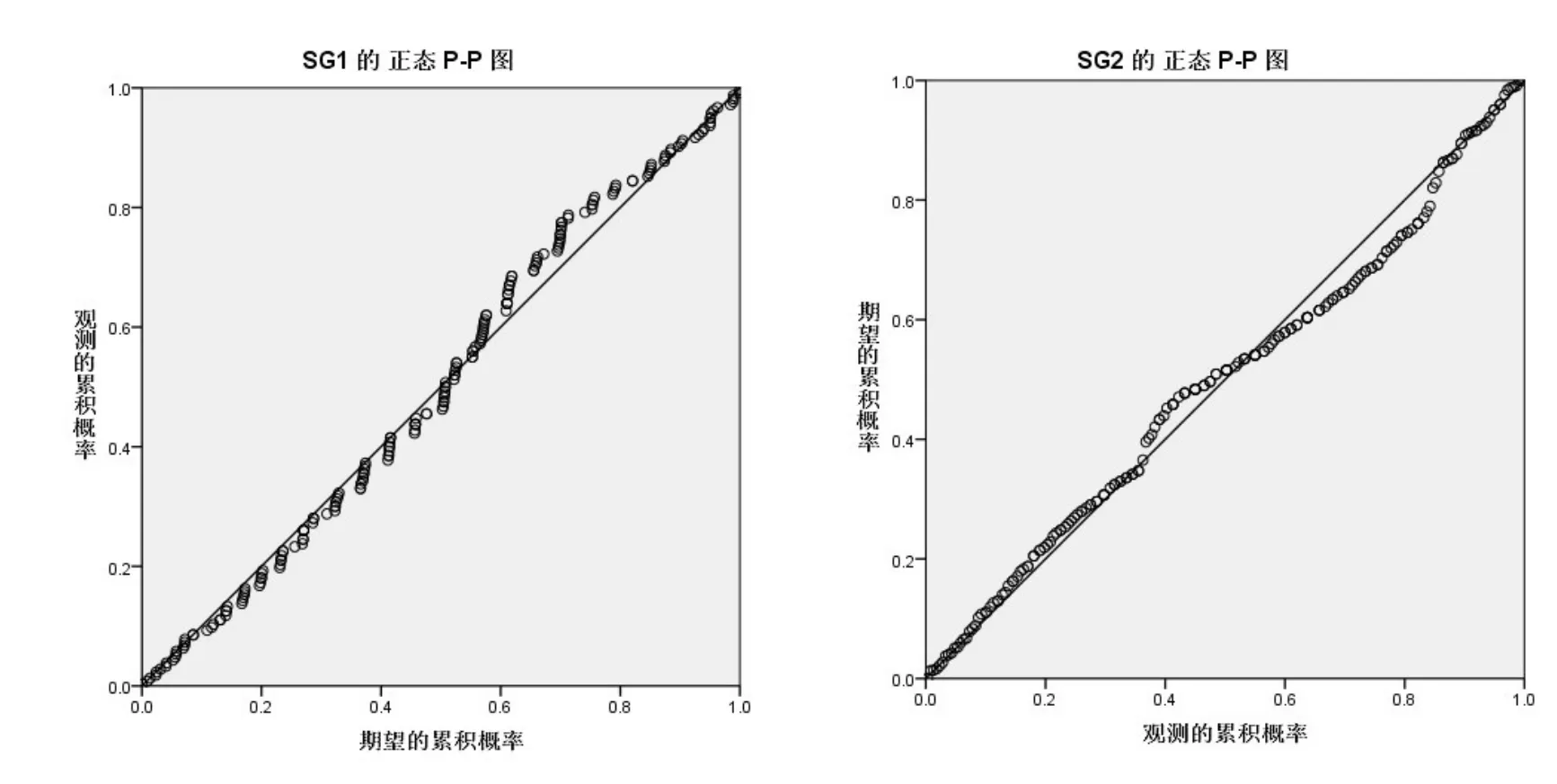
图4 三维扫描测量和手工测量的身高P-P概率图

由图4可以看出，正态P-P概率图中代表身高的的点大都簇在一条直线上。因此可以认为仪器测量数据与手工测量数据的分布相同，都近似服从正态分布。

（2）概率分析

经相关性分析，三维扫描数据和手工数据相关性为0.982，显著相关。

在经过概率分析发现：在均值基本相同的情况下，手工测量的数据相较于三维扫描的数据标准偏差较小，手工测量的数据较为稳定图5为身高的三维扫描（图5-b）和手工测量（图5-a）的频率直方图。

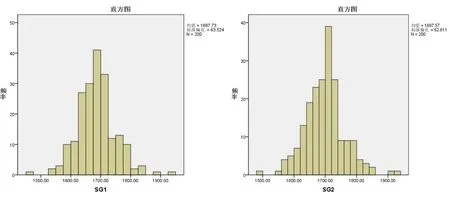
图5 身高的三维扫描数据直方图

2.2.2 身高的T检验

单样本的T检验用于对总体均值进行检验，是利用样本数据，检验当前的总体均值是否与事先假设的总体均值存在显著性的差异，即设样本x1,x2,……，xn来自于正态分布N(μ,σ2)，样本均值为，样本的标准差为 s2，对于均值μ的检验步骤如下：

①建立原假设H0：μ=μ0,H1：μ≠μ0。即原假设为总体均值与检验值之间不存在显著差异。

③利用原假设和样本数据计算t统计量和其他对应的p值。

④对比p值和α，结合原假设作出推断。如果p值＜α,则拒绝原假设，得出总体均值与检验值之间存在显著差异的结论；如果p值＞α,则不能拒绝原假设，应该认为总体均值与检验值之间不存在显著差异。

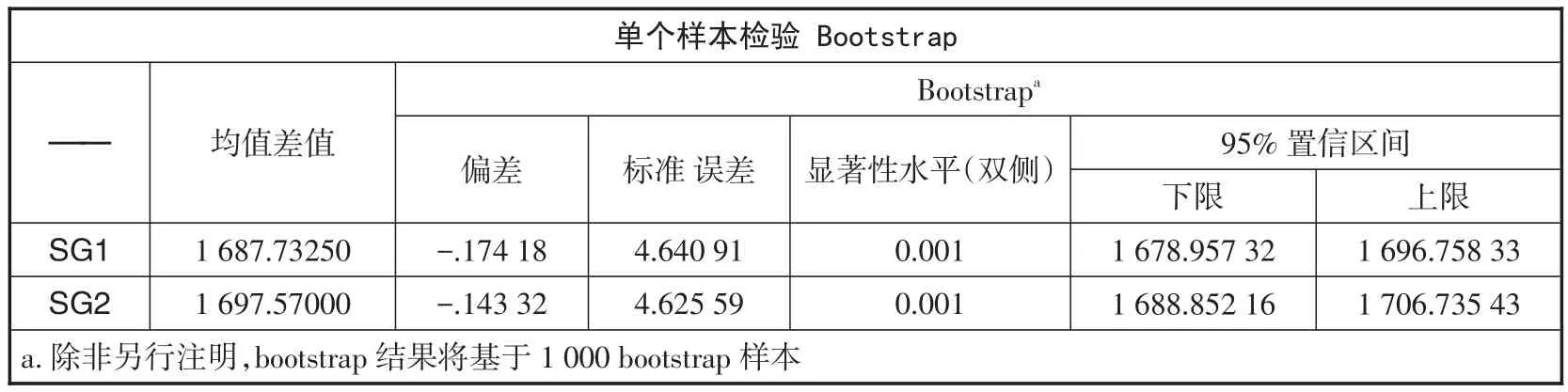
表5 身高测量数据的T检验结果

对两组数据进行T检验，在显著水平为0.05的情况下，结果显示显著性差异0.01＜0.05说明身高的仪器测量和手工测量两组数据有显著性差异，有必要对仪器测量数据和手工测量数据进行回归分析。

2.2.3 身高的相关分析

相关分析和回归分析是研究现象之间存在的相互关联的两种基本方法，其中相关分析用某个指标来表明现象之间相互依存关系的密切程度。选择三维扫描测量的数据为自变量，手工测量的数据作为因变量，进行相关分析。测定系数r2=0.964，即自变量三维扫描测量的身高数据可以解释为因变量手工测量数据的96.4%的变异。

同样的方法可以得到其他对比部位的相关系数：

表6 测量部位两组数据的相关系数

当0.8＜R＜1时，为高度相关；当0.5≤R＜0.8时，为中度相关；当0.3≤R＜0.5时，为低度相关：当0＜R＜0.3时，为不相关。所以除了会阴上部前后长的三维扫描和手工测量的数据为不相关，臂围的三维扫描和手工测量数据是中度相关外，其余部位的测量部位都为高度相关。

考察实验数据可知，根据表6的相关性分析，会阴高的三维扫描测量和手工测量没有相关性，两者测量所得数据相差较大，而根据数据显示会阴上部前后长的三维扫描数据普遍小于手工测量数据，且差距较大。其余部位的三维扫描数据普遍大于手工测量数据，但相差不大。

3 结论

本文通过对比200组男性人体测量数据，得到以下结论：

（1）考察实验数据可知，除了会阴上部前后长的三维扫描和手工测量的数据为不相关，臂围的三维扫描和手工测量数据是中度相关外，其余部位的测量部位都为高度相关。

（2）除去会阴上部前后长的三维扫描数据普遍小于手工测量数据外，其余部位的三维扫描数据普遍大于手工测量数据的趋势。

（3）除去会阴上部前后长，其余各部位的回归模型基本上呈线性关系。

（4）各部位的回归模型的准确率从高到低依次为：身高、会阴高、大腿围、上臂围。

根据综合分析得出结论：手工测量的数据相对三维扫描的数据精确度略高，但是二者相差不大，三维扫描测量速度快，使用便捷，具有广泛的应用空间。

参考文献：

[1]钱晓农.基于三维人体测量的人体体型细分识别的研究，纺织学报，2011，32(2)：107-120.

[2]王祺明.服装产业三维人体扫描技术的研究[M].绍兴文理学院学报，2007，（12）：51-55.

[3]国家技术监督局.服装人体测量的部位与方法GB/T16160[S].北京：中国标准出版社，1996.

[4]沙定国.实用误差理论与数据处理[M].北京：北京理工大学出版社，1993.

[5]潘力，王军，沙莎，于佐君.东北地区青年女子体型分类与服装档差研究[J].纺织学报，2013(11)：131-135