不同频率谐波下单芯电缆温度场仿真分析

张 磊，朱立翔，陈青云

（1.国网湖北省电力公司宜昌供电公司，湖北 宜昌 443000；2.武汉黉门电工科技有限公司，湖北 武汉 430073）

0 引言

我国电力电缆线路在电力系统中的使用量正逐年上升，尤其是高压交联聚乙烯（XLPE）绝缘电缆在电网中所占的比重日益增长，城区110 kV线路大量采用交联聚乙烯电缆[1-2]。随着电力电子器件的增加，谐波对其影响越来越大。谐波频率的不同，导线集肤效应和邻近效应会导致电缆交流电阻、阻抗的不同，而且谐波频率高，导线集肤效应和邻近效应使谐波电阻较基波电阻增大，因此谐波引起的电阻损耗导致的电缆温度升高问题不容忽略。

目前，从国内外发表的文献和著作来看，关于电力电缆温度计算的研究多数采用解析方法，文献[3-5]采用电缆热模型来计算电缆的损耗值，不能实际模拟电缆的运行状态，并且计算没有考虑谐波的影响。而数值法具有运算灵活、拓宽研究范围、减少实验的工作量等优点。

为了研究谐波下的电缆温度，本文以电磁场理论为基础，利用有限元数值计算，考虑趋肤效应和临近效应，结合电缆的敷设方式，分析缆芯损耗、屏蔽层损耗及绝缘层损耗，基于多物理场耦合的方法模拟出谐波情况下电缆的温度图，定性分析了谐波对电缆温度的影响，为电缆的热老化寿命评估奠定了基础。

1 电缆温度场计算原理

本文使用大型数值仿真软件Ansys作为电力电缆温度场仿真计算的工具，采用有限元的方法进行电缆的温度场建模与计算。本文研究对象为110 kV单芯电缆，电缆结构如图1所示。电缆的温度与电缆的敷设方式和排列方式有着密切的关系。地下电力电缆的敷设根据安装方式的不同分为：土壤直埋敷设、沟槽敷设和排管敷设。三相电力电缆在敷设时主要有两种排列方法，分别是三角形排列和一字形排列。土壤直埋敷设是最常用的电力电缆安装方式，本文以土壤直埋敷设方式下一字型排列的三相电缆为例进行仿真计算。

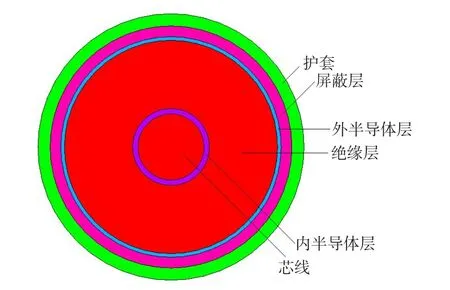
图1 单芯电缆结构图Fig.1 The structure of single core cable

当电力电缆正常工作时，电缆产生的热量在土壤中以固体传热的方式进行传递，这种传热方式为热传导，是指在物体内部或相互接触的物体表面之间，由于分子、原子及自由电子等微观粒子的热运动而产生的热量传递现象，这是在固体内的主要传热现象。当物体内部的不同部位之间存在温度差时，热量将会以热传导的方式从温度高的区域传递到温度低的区域[6-9]。若定义单位时间内流过单位面积的热流量为热流密度，用q表示，单位为 W/m2。热流密度与垂直于传热方向的温度变化率成正比，即

式中：φ表示通过面积A的总热量，称为热流量，单位为W；比例系数λ为材料的导热系数，单位为W/(m·K)。

由于电缆轴向长度非常大，一般认为轴向温度分布均匀，因此本文只考虑电缆的径向导热，不考虑三维轴向的导热。其稳态导热微分方程如下式所示，通过热源φ是否为0控制有无热源。

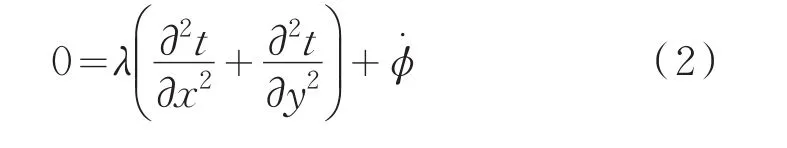
在求解导热微分方程时还需要已知边界条件，才能准确求得唯一的温度。导热微分方程主要包括三种边界条件[10-11]：

（1）第一类边界条件：边界温度场恒定不变且为已知量

式中：G为物体边界；T为已知温度值。

（2）第二类边界条件：研究场区边界上的热流密度分布已知

式中：k为导热系数，单位为W/(m·℃)；q为已知热流密度值，单位为W/m2。

（3）第三类边界条件：研究区域边界与周围流体的表面传热系数以及周围流体的温度已知

式中：a为对流换热系数，单位为W/(m2·℃)；k为导热系数，单位为W/(m·℃)。

2 电缆谐波损耗分析

谐波电流通过电缆时会使电力电缆在传输过程中产生有功损耗，散发出热量，进而表现为电缆各层的温度升高。电缆运行时，主要损耗分为电阻损耗与介质损耗。电阻损耗又分为缆芯的电阻损耗和金属屏蔽层的电阻损耗，而目前国内外大多数都通过公式计算的方法来计算电缆的电阻损耗，常常忽略了金属屏蔽层的损耗。本文通过有限元仿真的方法对绝缘层、缆芯、金属屏蔽层各自损耗进行计算来求解电力电缆总的有功损耗。

2.1 绝缘层介质损耗

电力电缆运行时在绝缘层上面会有比较高的电压，由此而引发的电力电缆损耗称为绝缘层损耗。对于普通单芯电力电缆，单位长度电缆的绝缘层损耗可以通过下式来计算，

式中：ω为角频率；U0为绝缘层对地相电压，单位为 V；tanδ表示绝缘损耗因素，可以查表得到；c为单位长度的电缆的电容，单位 F/m。通过时谐电场的仿真来计算电缆绝缘层的介质损耗。

2.2 缆芯损耗

电力电缆在通过交流电流时，缆芯的导体会发热产生焦耳热损耗，焦耳热损耗可以通过下式求得，

式中：W2为电力电缆缆芯导体单位长度的损耗；I为电力电缆中通过的电流；R为电力电缆单位长度的有效电阻，Ω/m。计算电力电缆缆芯导体的交流电阻需要考虑电缆在运行时的趋肤效应和临近效应，可以根据下式来计算，

式中：yp为邻近效应系数；ys为趋肤效应系数；R'为导体在工作温度下的直流电阻。电缆在工作温度下的直流电阻可以通过查表或者IEC-60287提供的公式计算得到[12-14]。在考虑趋肤效应和临近效应的情况下通过时谐磁场仿真来计算电缆的缆芯损耗。

2.3 金属屏蔽层损耗

电力电缆金属屏蔽层中的热损耗以两种形式体现，分别为环流损耗和涡流损耗。在计算电力电缆金属屏蔽层的损耗时，需要考虑电力电缆的导体芯数、排列方式、接地方式等因素。在工程实际应用中，为了减小金属屏蔽层中产生的环流，主要采用金属护套交叉互联的接地方式。因此本文研究的110 kV单芯交联聚乙烯电力电缆以交叉互联的方式接地，不考虑金属护套的环流，仅仅考虑由感应电压产生的涡流损耗。同样通过时谐磁场的仿真来计算金属屏蔽层由于感应出涡流而产生的焦耳热损耗。

3 电磁热耦合分析

目前关于电力电缆温度场的计算大多采用热路模型的方法来计算，计算过程中所需的导线热源是根据解析法进行计算得到的，作了比较多的假设和近似，如将该热源值均匀加载到输电线导体上求解电力电缆的温度场分布。虽然在计算导体交流电阻公式中考虑了导体的集肤效应以及导体电导率的温度(往往取导体最高允许温度)特性，但公式中用到的许多参数值大多都是经验值等等。这些假设和近似就导致了现有的计算方法都存在不够精确的缺点。因此，本文借鉴前人的研究成果，提出一种基于电磁-热耦合场的数值计算方法，即温度场计算所需热源通过电磁场部分计算得到，形成一种比较符合实际的数值计算方法。

电磁热耦合的方法同时考虑到了绝缘层损耗、缆芯损耗和屏蔽层损耗，并且也在计算中也考虑了导体之间的临近效应及交流电流下导体的趋肤效应，能更准确的计算出电缆的各层损耗。该方法先用电场仿真计算出绝缘层的损耗，在金属屏蔽层加载0电位，缆芯加载电压激励，计算得到绝缘层的电场分布，从而得到绝缘层的介质损耗；再利用磁场仿真计算出缆芯和屏蔽层损耗，电缆电磁场的麦克斯韦方程为[15-18]

式中：Je为涡电流密度；Js为源电流密度。

不同介质的交界面上电特性连续的方程为

式中n为法线方向上面的分量。

根据麦克斯韦方程，推导出电缆缆芯区域和金属屏蔽层矢量磁位方程

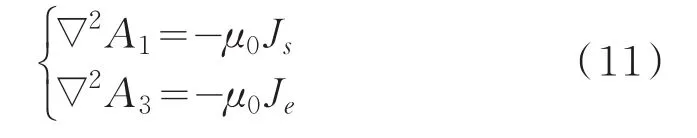
式中：Js为电缆缆芯的电流密度；A1为电缆导体的矢量磁位；Je为金属屏蔽层的涡流密度；A3为金属护套的矢量磁位。

电缆各层损耗的计算公式为

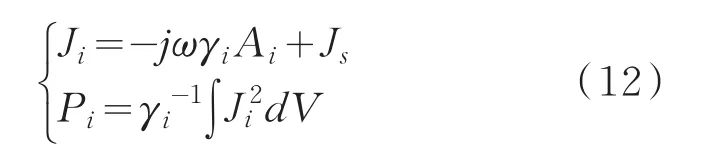
式中：Ji为各层电流密度；Ai为各层的矢量磁位；Pi为各层单位长度损耗功率；γi为材料的电导率。通过得到缆芯和金属屏蔽层的电流密度，从而得到缆芯和屏蔽层损耗。

将三种损耗作为热源导入到温度场进行仿真计算出电缆各层的温度及周围土壤环境的温度。与数值计算相比，有限元仿真的方法更准确地模拟了电缆的工作状态，而且比利用经验公式计算电缆的各层损耗要更加精确，为研究各次谐波情况下电缆的温升问题减小了误差。电力电缆在各次谐波电流下的温度计算流程图如图2所示。

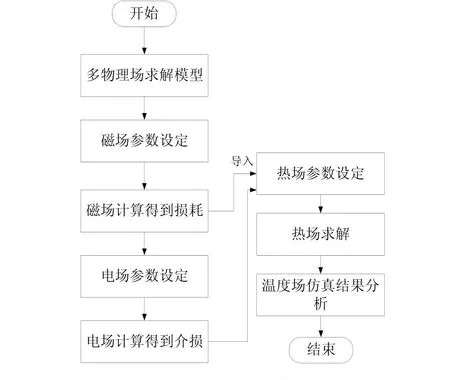
图2 电缆温度计算流程图Fig.2 The flow chart for calculating cable temperature

4 仿真分析

4.1 电缆模型及参数

根据图2，可以通过编程对不同谐波情况下电缆温度进行计算。对110 kV电缆进行各次谐波的仿真研究用的110 kV单芯XLPE电缆型号为YJLW03，电缆额定电压为110 kV，标称截面为1 000 mm2，电缆的截面图如图1所示，由内而外分别是芯线、内半导体层、绝缘层、外半导体层、屏蔽层和护套。电缆各层所用材料及尺寸参数如表1所示。线芯及金属屏蔽层的电阻率是查资料所得，其它各层均可以作为绝缘材料来处理，电阻率取值均为1×1014Ω·m，该型号电缆各层均没有非线性铁磁材料，因此相对磁导率取值均为1。

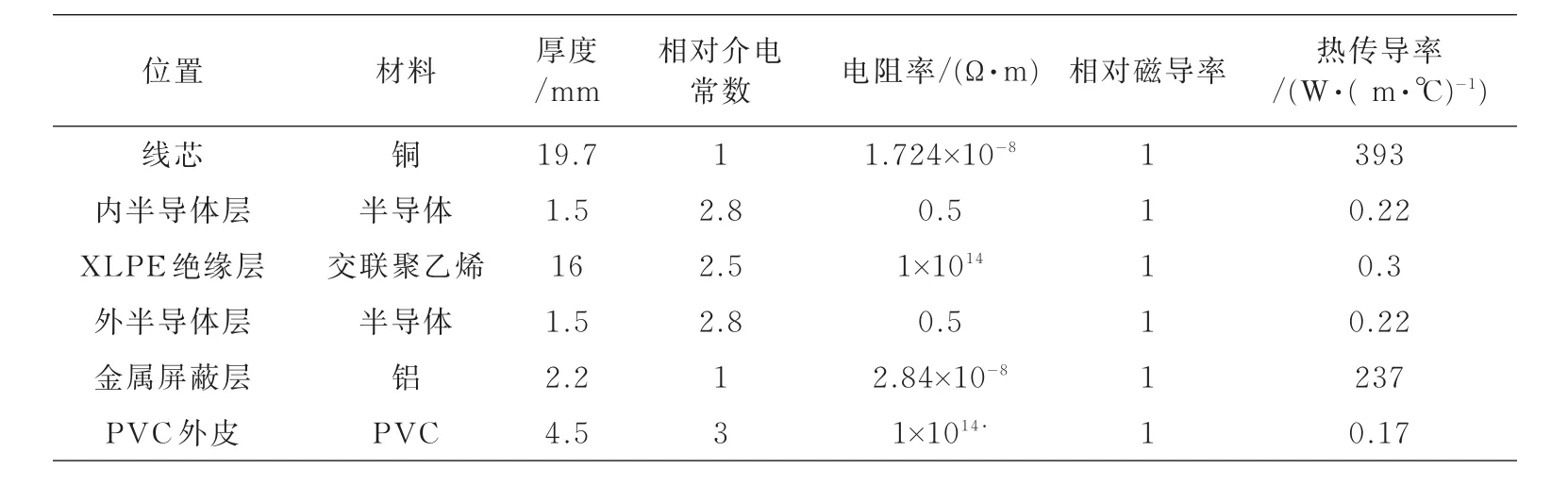
表1 电缆结构参数Tab.1 The parameters of cable structure

以土壤直埋敷设方式下的一字型排列的三相电缆作为研究对象，三相电缆的土壤直埋敷设示意图如图3所示。电缆的上下侧铺以砂层，紧邻砂层外侧是保护板，保护板外面是土壤[19]。按照电缆之间的彼此间距为2 m，上保护板距离地面的深度为8 m，上下保护板间的距离为3 m，砂层或软土对最近电缆的距离2 m，保护板的厚度0.8 m的参数进行三相电缆的敷设。周围环境相关物理参数如表2所示。采用 FEM 计算电缆的温度场分布，为提高计算效率，可将电缆的半无限大场转换成闭域场，即确定计算区域的边界，按有界场计算。结合相关文献可知[20-22]：温度仅在电缆附近变化较为剧烈，当远离电缆时，土壤温度将与环境温度相同。通常距离电缆2 m的土壤已不受电缆的影响。因此可取距离下保护板2 m的土壤作为下边界，取距离砂层外侧2 m的土壤作为左右边界。则土壤直埋敷设电缆的半无限大平面场可按有界场进行分析。对应的边界条件为：下边界条件为土壤温度恒定值，符合第一类边界条件；左右两边界条件的水平温度梯度为 0，符合第二类边界条件，即己知边界法向热流密度；地表边界对流换热系数和空气温度已知，符合第三类边界条件。

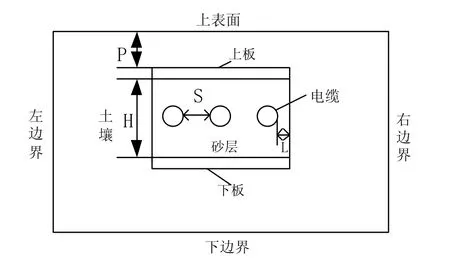
图3 电缆三相直埋示意图Fig.3 Three phase cable directly buried diagram

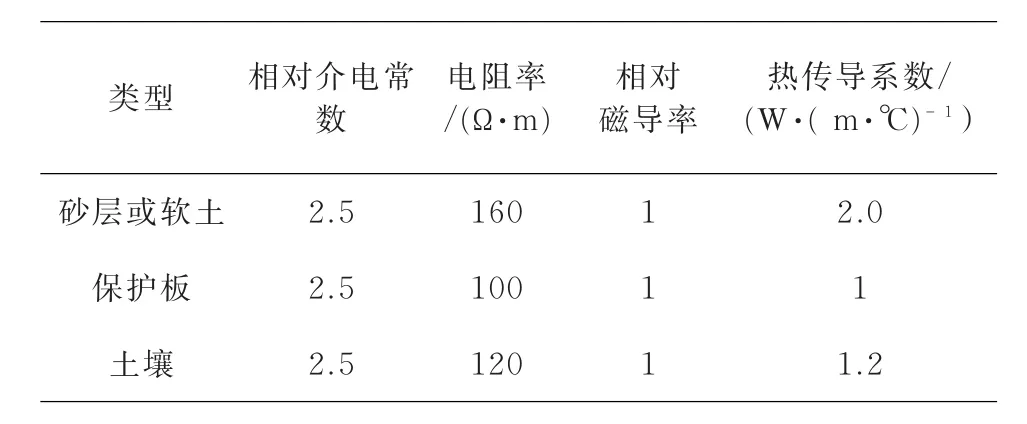
表2 周围环境参数Tab.2 The environmental parameters

4.2 仿真结果分析

根据图3所示电缆敷设示意图，结合表1和表2中的参数在ansys中建立三相电缆的模型。模型建立之后进行网格的剖分，网格剖分的是否合理直接影响最后的计算结果，因此为了得到更准确的温度，对于物理材料特性比较均匀的区域，如土壤区域，由于网格之间的方程与参数相同，网格剖分的相对而言会大一些；而对于电缆本体，材料的变化差异比较大，不同结构层的厚度也比较小，采用映射剖分的方式进行剖分，且使用三角形网格，剖分比较密，以得到更加准确的结果。

首先以50 Hz基波为例加载进行仿真计算，查询电缆手册可知，所使用的电缆载流量为500 A，故磁场仿真中加载幅值为50 Hz的电流，电场仿真加载110 kV电压，完成参数和边界条件设置后，对模型进行仿真，按照第3节中的流程计算电缆的温度。计算出基波情况下电缆的温度场如图4所示。电缆最高温度为29.2℃。

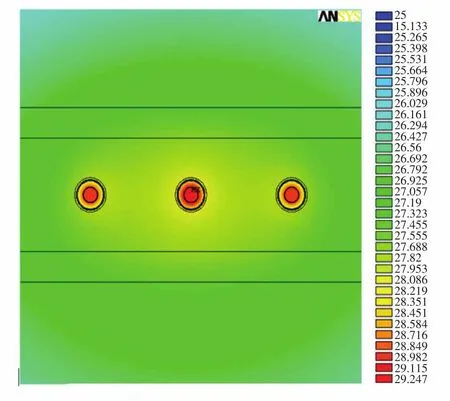
图4 电缆温度云图（单位：℃）Fig.4 The cable temperature nephogram

分别对电缆进行磁场和电场的仿真，可以得到缆芯损耗、屏蔽层损耗以及绝缘层的介质损耗。单根电缆的缆芯损耗和屏蔽层损耗密度图如图5所示，从图5可以看出热损耗在缆芯截面上呈非均匀分布，在缆芯表面附近达到最大值，这一分布与趋肤效应规律相吻合。单根电缆的介质损耗密度图如图6所示，从图6可以看出越靠近缆芯处的热损耗越大。

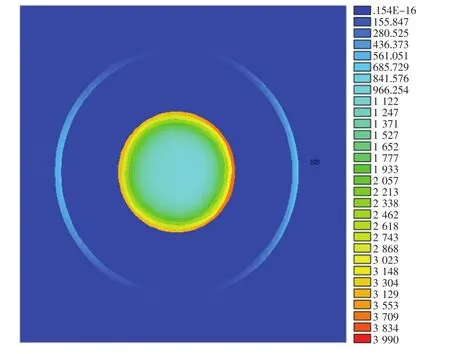
图5 单根电缆芯和屏蔽层损耗密度图（单位：W/m）Fig.5 The loss density figure of single cable core and shield

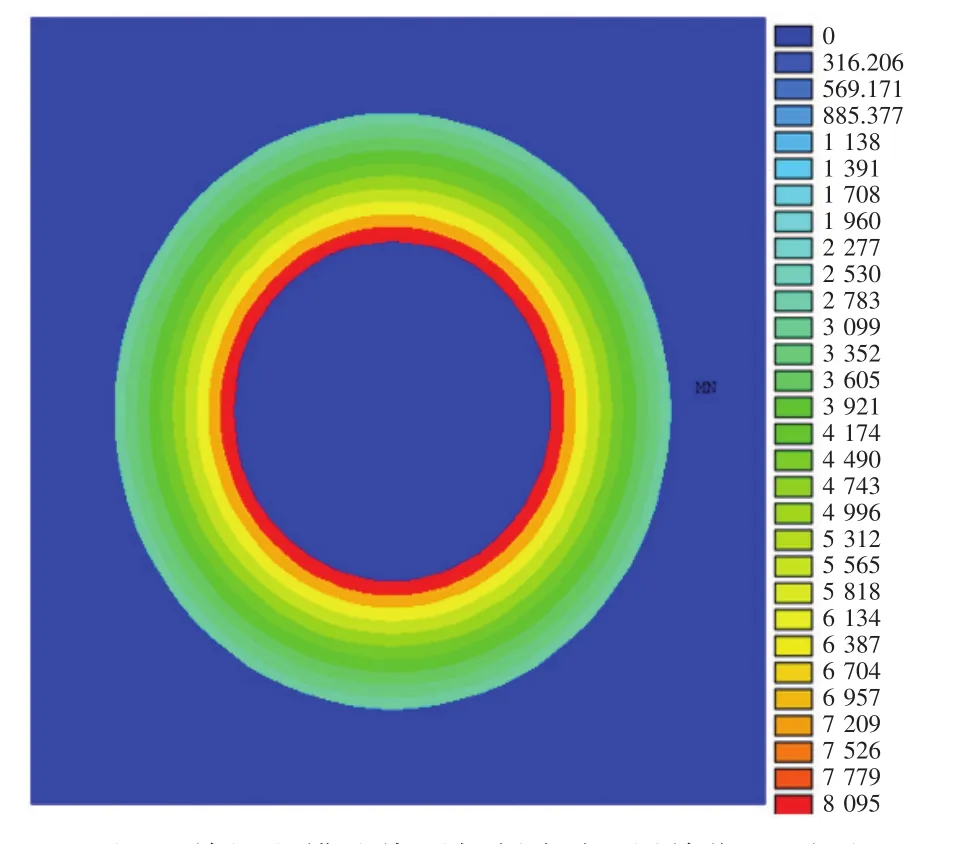
图6 单根电缆绝缘层损耗密度图（单位：W/m）Fig.6 The loss density figure of single cable insulation layer

按照同样的方法分别对电缆加载不同频率的谐波电流和电压进行仿真分析，分别计算出不同频率谐波下电缆的介质损耗及涡流损耗，如图7所示，频率越高，涡流损耗越大，这是由于高次谐波下趋肤效应的作用更加明显，电缆的等效电阻变大，因此损耗会增加，绝缘层介质损耗也会增加，但相对而言，介质损耗增加程度比电阻损耗小得多，说明高次谐波对趋肤效应的影响更加显著。

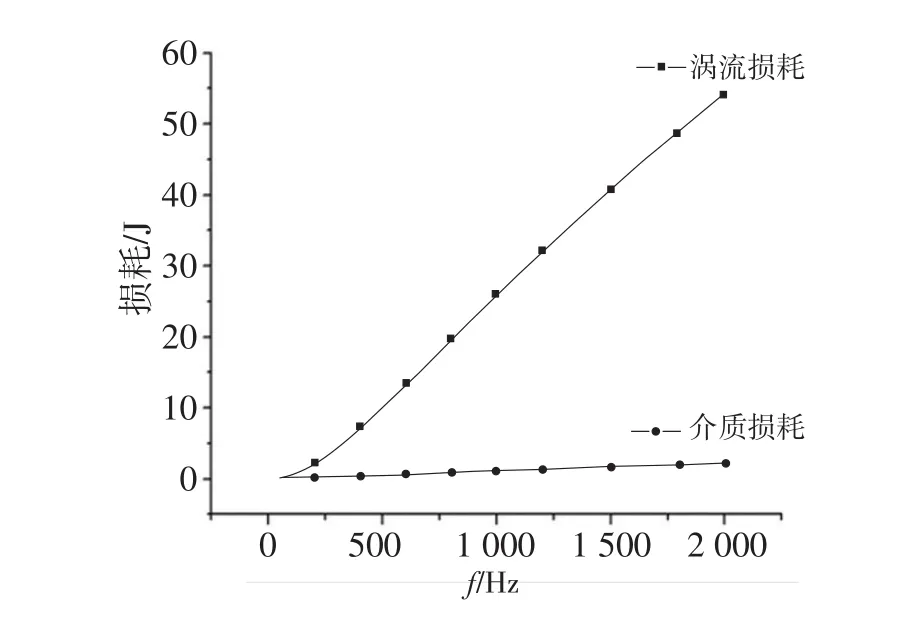
图7 频率对介质损耗和涡流损耗的影响Fig.7 The influence of frequency on the dielectric loss and eddy current loss

不同频率谐波下电缆温度变化如图8所示，在低频下，谐波对电缆温度影响不大，但是随着谐波频率的增加，高次谐波下，电缆的最高温度会显著上升。表面高次谐波对电缆温升有极大影响，会加速电缆的老化。

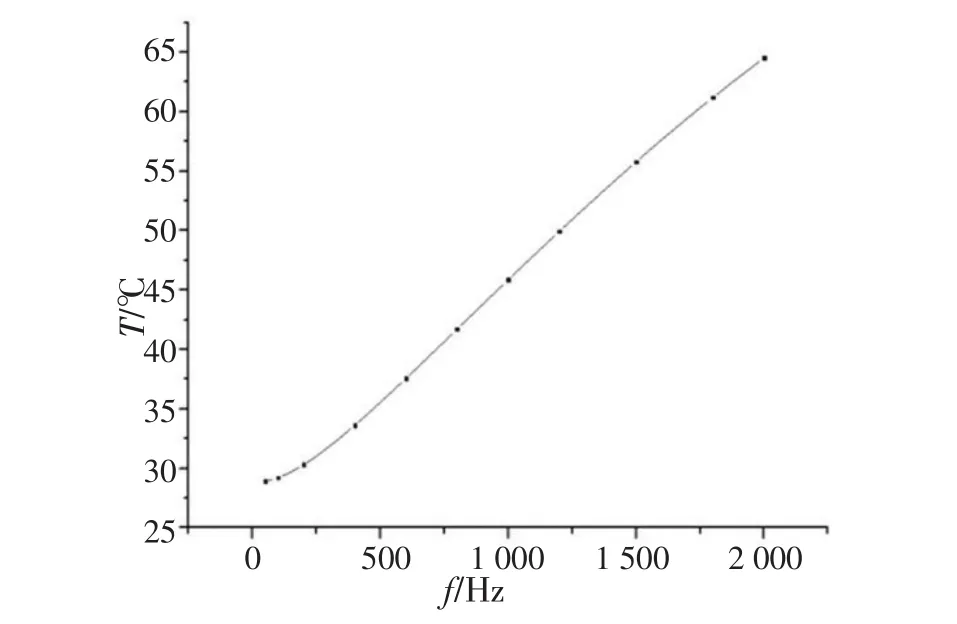
图8 电缆温度随频率变化图Fig.8 The cable temperature on frequency variation

5 结论

（1）分析了电力电缆的温度场计算原理，以及电缆焦耳热损耗的计算方法，电缆损耗包括绝缘层损耗、缆芯损耗和屏蔽层损耗，计算电缆的损耗需要考虑趋肤效应和临近效应，为后面的多物理场耦合模型提供了理论依据。

（2）建立了一种比较符合实际的电力电缆线路的电磁-热耦合模型，形成了多物理耦合场的有限元法的电力电缆输电线路在谐波下的温度计算方法。

（3）以土壤直埋敷设的110 kV单芯三相电缆为实例进行数值计算与分析。结果表明热损耗在缆芯截面上呈非均匀分布，在缆芯表面附近达到最大值，这一电流分布与趋肤效应规律相吻合，从而验证了模型和计算的正确性。

[参考文献]（References）

[1]李红雷，张丽，李莉华.交联聚乙烯电缆在线监测与检测[J].中国电力，2010，43(12)：31-34.LI Honglei,ZHANG Li,LI Lihua.Online monitor⁃ing and detection techniques of XLPE cables[J].Electric Power,2010,3(12)：31-34.

[2]曹晓珑，刘英，钟力生，等.从2010国际大电网会议看电力电缆技术的发展现状和趋势[J].高电压技术，2010，36(12)：3078-3083.CAO Xiaolong,LIU Ying,ZHONG Lisheng,et al.Power Cable Technology Status and trends seeing from the 2010 CIGRE conference[J].High Voltage Engineering,2010,36(12)：3078-3083.

[3]Olsen R S.Dynamic temperature estimation and real time emergency rating of transmission cables[C]//2012 IEEE Power and Energy Society General Meet⁃ing,2012.

[4]Olsen，Rasums.Modelling of dynamic transmission cable temperature considering soil-specific heat，thermal resistivity，and precipitation[J].IEEE Trans⁃actions on Power Delivery,2013,28(3)：1909-1917.

[5]陈诚.电缆沟敷设10 kV三芯电缆温度场计算及试验研究[D].广州：华南理工大学，2012.CHEN Cheng.The Computational and Experimental Rese-arch on 10 kV Three-core Cable Temperature Field of the Cable Trench[D].Guangzhou：South Chi⁃na University Technology,2012.

[6]刘毅刚,罗俊华.电缆导体温度实时计算的数学方法[J].高电压技术，2005，31(5)：52-54.LIU Yigang,LUO Junhua.Mathematical method of temperature calculation of power cable conductor in real time[J].High Voltage Engineering,2005,31(5)：52-54.

[7]赵建华,袁宏水,范维澄,等.基于表面温度场的电缆线芯温度在线诊断研究[J].中国电机工程学报,1999，19(11)：52-54.ZHAO Jianhua,YUAN Hongyong,FAN Weicheng,et al.Surface temperature field based online diagno⁃ses study for power cable's conductor temperature[J].Proceedings of the CSEE,1999,19(11)：52-54.

[8]梁永春,李延沐,李彦明,等.利用模拟热荷法计算地下电缆稳态温度场[J].中国电机工程学报，2008，28(16)：129-134.LIANG Yongchun,LI Yanmu,LI Yanming,et al.Calculation of the static temperature field of under⁃ground cables u sing heat charge simulation method[J].Proceedings of the CSEE,2008,28(16)：129-134.

[9]李志坚,张东斐,曹慧玲,等.地下埋设电缆温度场和载流量的数值计算[J].高电压技术，2004，30(4)：27-30.LI Zhijian,ZHANG Dongfei,CAO Huiling,et al.Numerical calculation of temperature field and cur⁃rent of underground cable[J].High Voltage Engineer⁃ing,2004,30(4)：27-30.

茄子棉铃虫主要啃食茄子茎及嫩芽，严重影响茄子的正常生长，及时进行防治。以幼虫蛀食蕾、花、果为主，也危害嫩茎、叶和芽。花蕾受害时，苞叶张开，变成黄绿色，2～3天后脱落。幼果常被吃空或引起腐烂而脱落，成果虽然只被蛀食部分果肉，但因蛀孔在蒂部，便于雨水、病菌流入引起腐烂，所以，果实大量被蛀会导致果实腐烂脱落，造成减产。

[10]王有元，陈仁刚，陈伟根，等.有限元法计算地下电缆稳态温度场及其影响因素[J].高电压技术，2008，34（12）：3086-3092.WANG Youyuan,CHEN Rengang,CHEN Weigen,et al.Calculation of static temperature field of bur⁃ied cable based on FEM and analysis of influential factors[J].High Voltage Engineering,2008，34（12）：3086-3092.

[11]梁永春，李彦明，柴进爱.地下电缆群稳态温度场和载流量计算新方法[J].电工技术学报，2007，22（8）：185-190.LIANG Yongchun,LI Yanming,CHAI Jin’ai.A new method to calculate the steady-state tempera⁃ture field and ampacity of underground cable sys⁃tem[J].Transactions of China Electrotechnical Soci⁃ety,2007,22(8)：185-190.

[12]IEC 602872321—1995 Calculation of the current rating of electric cables，part 3：Sections on oper⁃ating conditions,section 1：Reference operating conditions and selection of cable type[S].1995.

[13]IEC 602872121—1994 Calculation of the current rating of electric cables，part 1：Current rating equations(100% load factor)and calculation of losses,section 1：General[S].1994.

[14]IEC 602872122—1993 Calculation of the current rating of electric cables part 1：Current rating equations(100% load factor)and calculation of losses，section 2：Sheath eddy current loss factor for two circuit s in flat formation[S].1993.

[15]胡明丽.基于多物理场耦合模型的高压电力电缆温度场与载流量计算[D].广州：华南理工大学，2015.HU Mingli.Calculation of thermal distribution and ampacity for high-voltage power cables by using multi-physics coupled model[D]. Guangzhou：South China University of Technology,2015.

[16]孙国霞，舒乃秋，吴晓文，等.基于多物理场耦合的气体绝缘母线触头接触温升有限元计算[J].电工技术学报，2013，28（2）：408-413.SUN Guoxia,SHU Naiqiu,WU Xiaowen,et al.Fi⁃nite element analysis of contact temperature rise in gas insulated busbars based on coupled multi-physics[J].TransactionsofChinaElectro⁃technical Society,2013,28(2)：408-413.

[17]杨上兴.基于电磁－热耦合模型的直埋电缆载流量计算及间距的影响研究[J].电气应用，2015，34（19）：85-89.YANG Shangxing.Study on the effect of load flow calculation and spacing of buried cables based on electromagnetic thermal coupling model[J].Electro⁃technical Application,2015,34(19)：85-89.

[18]邱超.双回路单芯电力电缆不同敷设与排列方式下温度场与载流量计算[D].广州：华南理工大学，2013.QIU Chao.Calculations of thermal field and ampac⁃ity for two-circuit single-core power cables in dif⁃ferent laying modes and arrangements[D].Guang⁃zhou：South China University of Technology,2013.

[19]DL/T5221-2005城市电力电缆项目设计技术规定，2005.DL/T5221-2005 Technical rule for design of urban power cables，2005.

[20]孔祥谦.有限单元法在传热学中的应用[M].3版.北京：科学技术出版社，1998.KONG Xiangqian.ApplicationofFEM inheat transfer[M].3rd ed.Beijing：Science Press,1998.

[21]陶文铨.数值传热学[M].2版.西安：西安交通大学出版社，2001.TAO Wenquan.Numerical heat transfer[M].2nd ed.Xi’an：Xi’an Jiaotong University Press,2001.

[22]梁永春，柴进爱，李彦明，等.有限元法计算交联电缆涡流损耗[J].高电压技术，2007，33（9）：196-199.LIANG Yongchun,CHAI Jin’ai,LI Yanming,et al.Calculation of eddy current losses in XLPE cables by FEM[J].High Voltage Engineering,2007，33(9)：196-199.