特高压线路河网区域施工水面临时作业平台结构设计
2016-05-08徐侠松余秋安张志强
徐侠松,李 齐,余秋安,张志强,王 杰
(1.湖北省送变电工程公司,湖北 武汉 430063;2.武汉大学动力与机械学院,湖北 武汉 430072)
0 引言
特高压线路施工过程中,不可避免地要在水域进行作业。在传统情况下,施工设备在水上作业时一般采用专用的大型驳船或趸船,此方式具有结构简单,安全性高的优势。但是在河网区域河湖密集交织,河道较为狭窄且有通航限制,大型工程驳船或趸船无法进入到施工场地,因此这种方式无法满足施工要求。
针对河网区域的施工,目前国内常用的施工平台主要有双壁钢围堰平台[1]、钢管桩平台和浮式平台3种形式[2]。围堰平台刚度较大[3],但是需要大量使用钢套箱,经济性较差;钢管桩平台[4]的搭设难度较大,打桩速度较慢,资金投入太大。相比之下,浮式平台稳定性较好,移位方便,转场效率较高[5]。
本文开展了水面施工临时作业平台搭设结构及其施工稳定性等方面的研究,详细设计了适用于河网区域水面施工的浮式平台,并从稳定性和实用性等多个角度,采用理论与数值方法相结合的手段计算分析了该浮式平台的使用性能,为后期水上平台的设计施工提供了理论依据和设计参考。
1 浮式平台结构设计
由于水上施工平台要用于起重设备进行作业,考虑设备重量对平台的承载能力要求,以及平台整体转场施工的便利性,采用钢结构+浮筒的方式组装拼接成浮式平台,其中钢结构用于承受起重设备和塔材重量及施工过程中产生的惯性力和冲击等,浮筒仅用于提供浮力,浮筒与钢结构之间无直接连接。
根据施工设备的外形尺寸(长×宽×高为7 000 mm×2 000 mm×2 800 mm)、自重(7 000 kg)等关键参数确定平台的关键尺寸。平台布置图如图1所示,平台最大长度40 m,最大宽度20 m,总面积500 m2,在左右两侧各布置一条长为10 m,宽5 m的进出口走廊,用于起重机和塔材进场施工。
1.1 钢结构模块化拼接
钢结构整体由若干钢结构模块拼接而成,拼接后的三维效果如图2所示。钢结构上方铺有钢板,钢板与钢结构模块的型钢之间采用螺栓固接。单个钢结构模块重量为353.1 kg,且基本尺寸长×宽×高为5 m×2.5 m×0.01 m。钢结构模块的拼接方式包括铰接和螺栓固接两种方式,长边一侧采用螺栓固接,宽边一侧采用铰链销轴连接,这种连接方式使模块具有一定的柔性,虽然平台整体刚度降低,施工设备在平台上行驶或作业时垂向位移变大,但由于模块间可产生一定位移,使模块之间连接件受力条件改善,变形降低,降低了安装设计的难度。

图1 浮式平台布置图Fig.1 Layout of the floating platform

图2 浮式平台钢结构拼接后三维效果图Fig.2 3D model of the floating platform with splicing steel structure
1.2 浮体的选材与设计
浮体采用模块化工程浮筒拼接,单个浮筒尺寸为500 mm×500 mm×400 mm,壁厚7 mm,采用HDPE 5421B材料制成。浮体选用双层浮筒,每平米浮筒可具有0.3 t的浮力,因此如果浮体吃水深度相同,双层浮筒构建的500 m2浮体最大可以提供300 t浮力,远远超过平台上施工设备和所吊塔材的重量。
钢结构和浮体的模块化处理使实际应用中平台的尺寸便于调整,也方便了转场与现场安装,实现了平台的重复使用,满足工程中的经济性要求。
1.3 浮式平台岸边结构
在施工过程中,最危险的工况是在施工设备进入平台时,由于平台仅有少量浮体提供浮力,平台进口处产生较大的垂向位移,施工设备极易翻落水中。为了解决该问题,如图3所示,首先浮式平台岸边应做斜坡处理,且在浮式平台1 m区间做混凝土凹槽,并在浮式平台进口处底部布置支撑结构,从而使设备上下平台时,平台进口处底部与混凝土基础接触,起到支撑作用;其次在岸边与平台进口处采用两座钢结构踏板过渡,踏板在岸边的一端采用膨胀螺栓固定于混凝土斜坡处,在浮式平台的一端不做固定,任由浮式平台随浮体水位上下浮动时自由活动。

图3 浮式平台岸边结构Fig.3 Structures of the floating platform on river bank
2 浮式平台横倾稳定性分析
在施工作业进行时,由于受到施工设备和塔材重量及施工过程中产生的惯性力和冲击等的作用,平台会因平衡状态受到破坏产生倾斜。平台在外力干扰下产生倾斜会不会导致倾覆,在外力消失后能否回到原来的平衡位置,即抵抗外力的能力,是在平台设计过程中对其稳定性要考虑的问题[6]。本文主要考虑平台的横倾稳定性[7],即要计算平台在倾斜一定角度时的回复力矩[8]。本文采用等排水量法[9]计算分析。

图4 平台横倾后的横截面Fig.4 Cross-section of the tilted platform
如图4所示,选取平台的主视平面,根据计算得重心G(0,0.685 6 m),设重心位置不变,AB为初始平衡状态下的水线位置[10],平台在水线以下的部分为入水部分,入水高度为0.154 648 m,此时浮心为P点。当倾斜角度为α时,水线位置为A′B′,浮心位置为P′点。根据公式

计算回复力臂l,根据公式

计算回复力矩M。
计算利用MATLAB编程来实现,平台在横倾角α从0°增大到60°过程中,回复力矩的变化如图5所示。根据计算结果,平台在横倾角α=8.9°时达到最大值,约为13 158 kN·m。

图5 回复力矩与横倾角度关系Fig.5 Relationship between restoring momen and heel angle
但是,在施工过程中,浮式平台的倾斜角度很小,假设平台右侧达到出水的临界点,此时倾斜角α=0.443°,图6为浮式平台的横倾角在0°~0.443°变化时的回复力矩曲线。
由图6可以看出,当横倾角度较小时,可以近似认为回复力矩与倾角成正比关系。在当倾斜角度α=0.443°时,回复力矩M=6 374 kN·m。施工设备和塔材的自重所引起的力矩最大值为2 352 kN·m,在平台的横倾稳定性的安全范围内,满足安全要求。
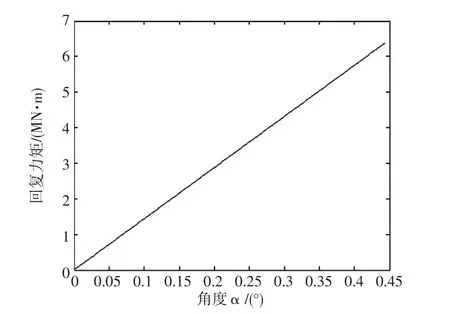
图6 小角度倾斜时回复力矩变化曲线Fig.6 Change curves of restoring moment in the range of small heel angle
上述稳定性分析是将平台看成一个刚性体进行的,但平台实际上由于搭接方式以及钢结构变形等,柔性较大,因此还需要通过数值计算方法进一步验证其实际使用性能。
3 浮式平台有限元模型的构建
为了合理模拟浮体及浮式平台在各种工况下的位移及受力情况,需要对不同构件采用对应单元进行网格划分,并根据所需解决的问题设置单元特性选项,定义实常数,最后形成整体有限元模型。
3.1 钢构模块中型材的模拟及整体钢结构的形成
建立构成整体钢结构的钢构模块时,本文采用3D线性有限应变梁单元[11]——BEAM188单元来模拟其型材以提高建模效率。针对钢结构模块间的销轴铰接和螺栓固接两种连接方式,本文采用自由度耦合(cp命令)和节点合并(nummrg命令)分别进行模拟。
3.2 钢构模块上铺钢板的模拟
为模拟上铺在钢构模块的钢板,采用SHELL63单元[12]来模拟,该单元是4节点弹性壳单元,具有弯曲和膜特性,能承受面内和法向荷载,可通过定义实常数来明确所模拟钢板的厚度,从而提高建模效率和计算速度。
3.3 浮筒组成的浮体浮力的模拟
浮筒组成的浮体,与钢结构之间没有直接连接,仅仅通过与钢结构之间的接触提供浮力,在建立有限元模型时需对浮体部分进行简化,但仍需考虑浮体所提供的浮力。
当载荷作用于浮式平台时,会引起浮式平台吃水的变化,从而引起浮式平台所受浮力的变化,这种由于结构排水体积变化引起的结构回复力的变化,可简化为与浮体面积成比例地均匀分布在浮式平台底部表面节点上的垂向弹簧,这些弹簧的垂向刚度总体上与单位吃水变化引起的浮力变化等效,称其为水弹簧[13]。采用COMBIN14单元以模拟水弹簧(即浮体的浮力)作用。
基于吃水与排水量的线性关系,通过计算可得单个钢构模块底部型材各节点的水弹簧刚度。以单个钢构模块为例,单个钢构在吃水深度h下所受浮力为

上式中S底为单个钢构模块底部面积,即S底=5 m×2.5 m=12.5 m2。单个弹簧的轴力为

上式中ki为该弹簧的刚度。根据水弹簧的定义则有
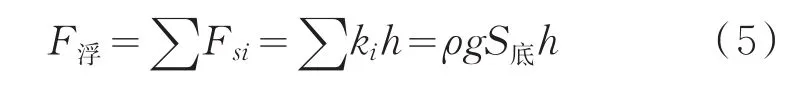
因此可得钢构模块底面垂向水弹簧刚度为ki=ρgS底∑,由于钢构模块需通过组装形成整体钢结构,组装完成后钢构模块的角点节点处存在4个水弹簧,边缘节点处存在2个水弹簧,中间节点处仅有1个水弹簧,因此角点节点、边缘节点和中间节点处的弹簧刚度应不相同。具体数值如表1所示。

表1 钢构模块底部垂向水弹簧刚度Tab.1 The stiffness of vertical water spring on the bottom of the steel structure module
3.4 锚固定位系统锚绳的模拟
为了保证浮式平台的正常工作,需布置锚固定位系统[14]。本文中采用锚泊定位方式,即铁锚通过锚绳与浮式平台上的带缆桩连接,实现浮式平台的固定。锚固定位系统中的锚绳只能抗拉不能抗压,因此采用LINK180单元进行模拟。
3.5 浮式平台进口底部支撑结构的模拟
当设备进入平台时,支撑结构与底部混凝土基础接触,当设备走过一段距离后,支撑结构由于浮体浮力又脱离与混凝土基础之间的接触。由此可知,支撑结构与混凝土基础之间接触与否,与起重设备或塔材在平台上的位置相关,属于典型的由接触引起的边界非线性问题[15]。
在实际计算中,如果采用接触单元和目标单元对上述接触行为进行仿真,必然造成计算规模过大的问题,因此本文采用非线性弹簧COMBIN39对支撑结构和混凝土基础之间的作用力进行模拟。最终形成的浮式平台有限元模型如图2所示,各单元数量如表2所示,节点总数为76 176个。

表2 单元数量表Tab.2 Number of various units
4 不同工况计算结果及分析
4.1 不同工况
浮式平台在工作时,需要对平台受到的各种荷载,进行各种工况的荷载组合分别进行验算。由于浮式平台是在基本上无流速的库区搭建,故忽略浮式平台所受的流水压力、波浪力及风力,仅考虑浮式平台受到的垂向荷载和静水压力的作用。
浮式平台所受到的垂直荷载有40个钢构模块自重(14 124 kg)、钢板自重(31 200 kg)、履带式起重机自重(7 000 kg)和最大吊重(5 000 kg)、浮体重量(32 000 kg)等。
采用以下5个工况对浮式平台进行静力学分析:
工况一:平台有限元模型形成后,仅对平台受到的平台自重以及湖水静水压力进行加载,用于验证浮式平台分析模型的正确性。
工况二:施工设备进入平台使其受载后,进口底部支架与混凝土基础接触,利用该工况判断进口处钢结构及底部支架是否满足实际工程要求。
工况三:施工设备位于进口廊道中部位置,即钢构模块的铰接区域,利用该工况判断进口廊道产生的最大垂向位移是否满足实际工程要求。
工况四:施工设备到达施工工位处,拟起吊的塔材到达起吊区域,该工况用于判断整体平台在使用过程中是否满足实际工程要求。
工况五:施工设备到达施工工位处,并开始进行起吊,该工况可能会导致浮式平台产生倾斜坡度过大的问题,并且施工设备所在区域可能存在钢构模块或钢板应力集中的情况,此工况用于判断整体平台在使用过程中是否满足实际工程要求。
4.2 计算结果及分析
有限元分析后,可得以下结论:
(1)在工况一中,浮式平台整体垂向位移分布如图7所示,通过分析可得有限元分析的平均吃水深度为0.155 7 m。基于吃水与排水量的关系,通过理论计算可得到浮式平台理论吃水深度为0.154 6 m。由此可知理论分析结果与有限元计算结果非常接近,误差仅为0.6%,由此可以验证浮式平台分析模型的正确性。

图7 浮式平台垂向位移分布(工况一)Fig.7 Vertical displacement contour of the floating platform in operation condition 1
(2)在工况二中,浮式平台进口处钢结构以及底部支撑结构在该工况中受力较大,最大综合应力为154 MPa,如图8所示,满足强度要求。

图8 进口处钢结构综合应力分布(工况二)Fig.8 Stress contour of steel structure at the entrance of the platform in operation condition 2
(3)工况三中,当施工设备位于距离进口5 m处,即钢构模块铰接位置,平台进口廊道会产生较大垂向位移,浮式平台整体垂向位移如图9所示,最大垂向位移为-0.547 m,发生在两钢构模块连接处,如果浮体采用单层浮筒构建,该处将由于受到施工设备较大的自重载荷浸入水中,由此实际工程中应采用上下两层浮筒形成浮体。

图9 浮式平台垂向位移分布(工况三)Fig.9 Vertical displacement contour of the floating platform in operation condition 3
(4)在工况四中,浮式平台整体上铺钢板在该工况下综合应力分布如图10所示,最大综合应力为305 MPa,已超过了材料屈服极限,发生在平台左侧边缘处,与起重设备工位和塔材(塔材中心距离平台左侧边缘2.5 m)堆放位置比较靠近平台左侧边缘有关,因此在平台实际使用工况中,应注意塔材堆放位置以及起重设备工位与平台边缘之间的距离,图11为塔材堆放位置与最大综合应力之间的变化趋势,由图可知,随着塔材堆放位置与平台左侧边缘距离的增大,最大综合应力快速降低,降低趋势近似于线性,图12为塔材中心距离平台左侧边缘3.5 m时钢板综合应力分布情况,最大综合应力已经降为142 MPa,满足强度要求。

图10 浮式平台钢板综合应力分布(工况四)Fig.10 Stress contour of steel plates on the floating platform in operation condition 4

图11 塔材堆放位置与最大综合应力间的变化趋势Fig.11 Relationship between the materials stack position and maximum stress

图12 修正后钢板综合应力分布(工况四)Fig.12 Stress contour of steel plates after amendment in operation condition 4
(5)工况五为平台受载情况最危险的工况,分析后浮式平台整体垂向位移如图13所示,位移较大区域明显增大;浮式平台钢结构综合应力分布如图14所示,最大综合应力为278 MPa,钢构模块连接位置存在局部应力集中情况,后期在工程实际施工中,钢构模块连接区域应进行补强处理。

图13 浮式平台垂向位移分布(工况五)Fig.13 Vertical displacement contour of the floating platform in operation condition 5

图14 钢结构综合应力分布(工况五)Fig.14 Stress contour of steel structure in operation condition 5
5 结语
本文针对某特高压工程湖北河网区域施工特点,开展了水面施工临时作业平台搭设结构及其施工稳定性等方面的研究,详细设计了水面施工临时作业平台,并对钢构和浮体的模块化拼接方式、岸边支撑结构进行了详细介绍;并通过横倾稳定性理论计算,验证了平台的回复力矩等参数在理论上已达到实际工程要求;最后本文利用有限元方法,对多个工况进行了静力学分析,充分验证了平台的刚度和强度等均能够满足实际工程要求。本文研究成果可为后面水面临时作业平台的具体实施提供参考依据。
[参考文献](References)
[1]汤德强,杨波.钢浮筒浮平台拼装大型双壁钢围堰施工技术[J].安徽建筑,2014(3):112-114.Tang De-qiang,Yang Bo.Construction technology of assembling large double wall steel cofferdam with steelpontoon [J].AnhuiArchitecture,2014(3):112-114.
[2]廖文华.库区深水裸岩高桩承台施工浮式平台设计研究[J].铁道标准设计,2013(2):61-63.Liao Wen-hua.Design research of floating platform for high pile cap construction with exposed rock in deep water in reservoir region[J].Railway Standard Design,2013(2):61-63.
[3]李险峰.深水基础双壁钢围堰水水上平台下沉施工工法[J].铁道建筑,2005(12):24-26.Li Xian-feng.Construction method on sinking of double-walled steel cofferdam from platform on water for casting deep-water foundation[J].Railway Engi⁃neering,2005(12):24-26.
[4]定梁龙,旷新辉,乔春柳,等.库区深水墩钢管桩平台浮法施工技术[J].世界桥梁,2012,40(5):41-44.Ding Liang-long,Kuang Xin-hui,Qiao Chun-liu,et al.Floating method in construction of platform sup⁃ported by steel pipe piles for deep water pier in res⁃ervoir region[J].World Bridges,2012,40(5):41-44.
[5]王西苑.浅谈浮式平台在深水基础施工中的应用[J].今日科苑,2009(18):111.Wang Xi-yuan.Brief introduction to application of floating platform in deep-water foundation[J].Mod⁃ern Science,2009(18):111.
[6]盛振邦,刘应忠.船舶原理[M].上海:上海交通大学出版社,2013.Sheng Zhen-bang,Liu Ying-zhong.Principle of Na⁃val Architecture[M].Shanghai:Profile of Shanghai Jiao Tong University Press,2013.
[7]王少青,张吉平.船舶横倾航行的稳性[J].大连海事大学学报,2002,28(3):31-33.Wang Shao-qing,Zhang Ji-ping.Stability ofthe ship being listing for a certain angle[J].Journal of Dalian Maritime University,2002,28(3):31-33.
[8]蒋维清.船舶原理[M].大连:大连海事大学出版社,1999.Jiang Wei-qing.Principle ofNavalArchitecture[M].Dalian:Dalian Maritime University Press,1999.
[9]黄鑫锋.应急气囊对直升机漂浮稳定性的影响[D].南京:南京航空航天大学,2011.Huang Xin-feng.Stability analysis of the helicop⁃ter with flotation bags[D].Nanjing:Nanjing Uni⁃versity of Aeronautics and Astronautics,2011.
[10]唐伟峰,孙锦.某浮体漂浮稳定性研究[J].海军航空工程学院学报,2012,27(5):521-524.Tang Wei-feng,Sun Jin.Research on the floating stability to the floating body[J].Journal of Naval Aeronautical and Astronautical University,2012,27(5):521-524.
[11]王勖成.有限元法[M].北京:清华大学出版社,2002:302-323.Wang Xu-cheng.Finite Element Method[M].Bei⁃jing:Tsinghua University Press,2002:302-323.
[12]张洪信,管殿柱.有限元基础理论与ANSYS11.0应用[M].北京:机械工业出版社,2009:240-246.Zhang Hong-xin,Guan Dian-zhu.Finite Element Theory and Applications of ANSYS11.0[M].Bei⁃jing:China Machine Press,2009:240-246.
[13]唐世江.桥梁施工浮式平台的静动力分析[D].湘潭:湘潭大学,2014.Tang Shi-jiang.Static and dynamic analysisof floating platform on bridge construction [D].Xiangtan:Xiangtan University,2014.
[14]杨欢,王磊,李欣.锚泊辅助动力定位研究与进展[J].实验室研究与探索,2014,31(4):88-92.Yang Huan,Wang Lei,Li Xin.Review of the re⁃search on thruster assisted position mooring sys⁃tem[J].Research and Exploration in Laboratory,2014,31(4):88-92.
[15]周宁.ANSYS-APDL高级工程应用实例分析与二次开发[M].北京:中国水利水电出版社,2007:234-286.Zhou Ning.Engineering Example Analysisand Secondary Development of ANSYS-APDL[M].Bei⁃jing:China Water&Power Press,2007:234-286.
