大斜度井各向异性地层双感应测井响应特征研究

范宜仁, 巫振观, 王磊, 刘家雄, 李格贤

(中国石油大学地球科学与技术学院, 山东 青岛 266580; 中国石油大学CNPC测井重点实验室, 山东 青岛 266580)

0 引 言

大斜度井、水平井数量不断增加,人们直接利用大斜度井、水平井的电阻率曲线进行油气评价时,往往产生偏差[1],给测井解释带来困惑,井斜角及各向异性对测井响应的影响开始受到关注。汪宏年等[2]总结分析了各向异性地层中普通电阻率测井、侧向测井及微球型聚焦测井的响应特征。人们对倾斜各向异性地层中双侧向测井和随钻电磁波测井都做了较深入的研究,倾斜各向异性地层中,双侧向电阻率曲线不仅形态发生变化[3],深、浅电阻率差异也变得更为复杂[4]。范宜仁等[5]推导了各向异性地层中磁偶极子源产生的磁场,并模拟了倾斜各向异性地层中随钻电磁波测井响应。作为电测井方法,感应测井在斜井中的测量同样受到井斜角、地层倾角和各向异性的影响。1986年,R.H.Hardman等[6]研究了双线圈系在倾斜地层中的感应测井响应特征,人们认识到井斜角度对感应测井具有重要的影响。以双线圈系为基础的双感应测井同样受井斜角影响严重[7-9],斜井中感应测井视电阻率也与直井相差甚远,而电测井响应是储层流体饱和度评价的最主要依据[10],因此,直接利用斜井条件下测量值进行评价时存在较大的问题。在各向异性地层中,各向异性与井斜角的共同作用使得感应测井响应更加复杂[11]。胡松等[12]利用三维数值模式法研究了水平井各向异性地层的双感应测井响应,分析了其影响因素。但是,中国关于斜井双感应测井的研究主要是针对各向同性地层,各向异性地层中的双感应测井响应以及各向异性校正的研究较少。

本文不考虑井眼及侵入等影响,主要针对层状各向异性地层,研究大斜度井/水平井双感应测井响应特征及对各向异性敏感性。首先,基于赫兹矢量位函数方法,将任意方向磁偶极子源分解为水平磁偶极子源和垂直磁偶极子源进行求解,并推导了磁偶极子源在各层中的磁场。进而讨论了各向异性地层中地层厚度、电阻率对比度、各向异性系数以及井斜角对双感应测井响应的影响。在此基础上,建立了不同井斜角度下各向异性校正图版,为测井解释及储层有效评价提供了技术支持。

1 双感应测井响应计算方法

图1 三层层状地层模型

图1为层状各向异性地层模型,第2层为目的层,上下为无限厚围岩。图1中,ε1、ε2、ε3为各层介电常数,μ1、μ2、μ3为各层磁导率,σh1、σh2、σh2为各层水平电导率,σv1、σv2、σv3为各层中垂直电导率。

感应测井计算常将发射线圈近似为磁偶极子源(M),在倾斜地层或斜井中,磁偶极子源可沿地层层理方向和垂直方向分解为水平磁偶极子源(Mh)和垂直磁偶极子源(Mv)。为便于求解,引入赫兹矢量位π,对于垂直磁偶极子而言,仅有沿垂直方向的分量πz,而水平磁偶极子,则既有垂直方向分量πz,又有水平方向分量πx[12]。因此垂直磁偶极子可用标量πz表示,其在各向异性地层中

kρJ0(kρρ)dkρ

(1)

(2)

(3)

(4)

水平磁偶极子可用沿水平方向的标量πx和沿垂直方向的标题πz表示,各向异性地层各层中,赫兹矢量位为

kρJ0(kρρ)dkρ

(5)

(6)

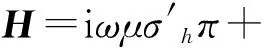
(7)

(8)

(9)

式中,Ai、Bi、Pi、Qi、Si、Ti为系数,可由层界面处边界条件确定;βi表示磁偶极子源所在层,当源位于第i层时,βi=1,否则βi=0。

图2 直井条件下不同层厚时深中感应测井响应

由磁场可进一步计算接收线圈感应电动势,并得到双线圈系视电导率[6]。双感应测井仪器是由双线圈系为基础的复合线圈系,其视电导率可由双线圈系视电导率结合仪器参数获得[13-14]。本文以1503双感应测井仪为例,探讨各向异性地层双感应测井响应特征及规律。考虑实际双感应测井仪器提供的数据都经过了反褶积处理和趋肤效应校正,本文的深感应测井响应作了三点反褶积[15],深感应测井响应和中感应测井响应都作了趋肤效应校正[16-17],不考虑相位移误差[18]。

2 数值模拟结果分析

2.1 地层厚度的影响

建立图1所示水平三层层状地层模型,目的层电阻率为10 Ω·m,上下围岩电阻率都为1 Ω·m,不考虑侵入及井眼影响;图2为直井条件下双感应测井响应随目的层厚度变化。可以看出,随着层厚的增大,深中感应测井响应目的层视电阻率不断增大,趋于目的层真实电阻率。同时,深感应测井响应明显关于目的层中点对称,而中感应测井响应则不对称,这是双感应测井仪器结构决定的。

图3为不同围岩电阻率条件下地层厚度在0.1～16 m变化时目的层视电阻率随层厚变化,其中双感应视电阻率取目的层中点值。可以看出,目的层厚度越小,围岩电阻率越低,双感应视电阻率误差越大,难以反映目的层真实电阻率。从图3可知,当目的层厚度小于2 m时,深中感应测井响应受围岩影响严重,目的层厚度大于10 m时,深感应测井响应几乎不受围岩影响,而中感应测井响应在目的层厚度大于8 m时,不再受围岩电阻率影响。

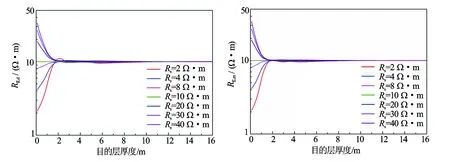
图3 不同围岩电阻率下深中感应测井响应随目的层厚度变化

2.2 电阻率对比度的影响

为系统分析不同地层电阻率对比度条件下大斜度井水平井中双感应测井响应,针对单界面地层模型进行模拟,取地层总厚度为10 m,目的层、围岩厚度分别5 m,围岩为各向同性,电阻率为1 Ω·m,井斜角为85°;目的层分各向同性和各向异性讨论,各向同性目的层,电阻率对比度取2∶1、5∶1、10∶1、15∶1、20∶1和25∶1,各向异性目的层各向异性系数为3,水平电阻率与围岩电阻率比值为2∶1、5∶1、10∶1、15∶1、20∶1和25∶1。

图4 不同地层对比度下深中感应测井响应

图4为不同地层对比度下深中感应测井响应曲线。可以看出,在大斜度井各向同性地层和各向异性地层的视电阻率曲线在边界处都会产生极化角,其形态及视电阻率值受地层对比度影响严重。不论是各向同性地层还是各向异性地层,深感应测井曲线在边界处产生的极化角在深度范围上达到0.7 m左右,在中感应测井曲线上达到0.5 m左右,这在测井解释过程中很容易被错误地解释为1个单独的高电阻率层。另一方面,各向异性地层中的深中感应视电阻率都远大于各向同性地层,给地层评价带来极大的干扰。此外,随着地层对比度的增大,深中感应视电阻率曲线极化角越明显,其形态也越尖锐。相比之下,中感应视电阻率极化角比深感应要小得多,各向异性地层的极化角远大于各向同性地层。

图4中可以看出,当地层对比度为2时,几乎分辨不出极化角,这也表明极化角的产生并不只是井斜角唯一决定的,与地层对比度也密切相关。

2.3 各向异性系数的影响

为表征各向异性的强弱,将垂直电阻率与水平电阻率比值的开平方定义为各向异性系数,用λ表示,即

(10)

式中,Rv为垂直电阻率;Rh为水平电阻率;λ为各向异性系数。

图5 不同各向异性系数下双感应视电阻率随井斜角变化

2.3.1 无限厚地层

为研究各向异性系数对双感应测井响应影响,设地层无限厚,地层水平电阻率分别为1、10 Ω·m和100 Ω·m,各向异性系数取值为1～7,模拟井斜角从0°～85°变化时双感应视电阻变化。

图5为不同各向异性系数下双感应视电阻率随井斜角变化。图5可以看出,当各向异性系数为1,即地层为各向同性介质时,深中感应视电阻率不随井斜角度变化。而当各向异性系数大于1时,斜井、水平井中双感应响应将受到各向异性影响。当各向异性系数确定时,随着井斜角的增大,双感应视电阻率不断增大。井斜角小于30°时,各向异性引起的视电阻率变化小,各向异性对深感应响应的影响可以忽略;井斜角大于30°时, 各向异性引起的深感应响应增大显著,需考虑各向异性校正。

2.3.2 多层各向异性地层

测井面临的地层往往依物性的不同层状分布,而不是简单地视为无限厚介质。为了研究层状地层中各向异性影响,建立图1所示三层地层模型。设目的层为各向异性地层,水平电阻率为10 Ω·m,围岩为电阻率1 Ω·m的各向同性地层。图6为井斜80°条件下,各向异性系数分别为1、2、3时,双感应测井响应。

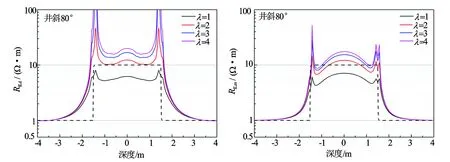
图6 层状各向异性地层双感应测井响应

从图6可以看出,随着各向异性系数增大,目的层视电阻率逐渐增大,界面处犄角迅速增大。这表明,在层状地层大斜度井中的双感应测量结果受各向异性影响严重。本文建立的模型条件下,各向同性地层(λ=1)大斜度井中,当目的层厚度较小时,由于受围岩影响严重,双感应测量值小于目的层真实电阻率,而各向异性的存在,又使得目的层视电阻率增大,两者的相互作用使得双感应测井响应极为复杂。因此,在进行大斜度井测井评价时,需要结合实际情况,充分考虑主要影响因素,进行层厚校正或是各向异性校正。

2.4 井斜角的影响

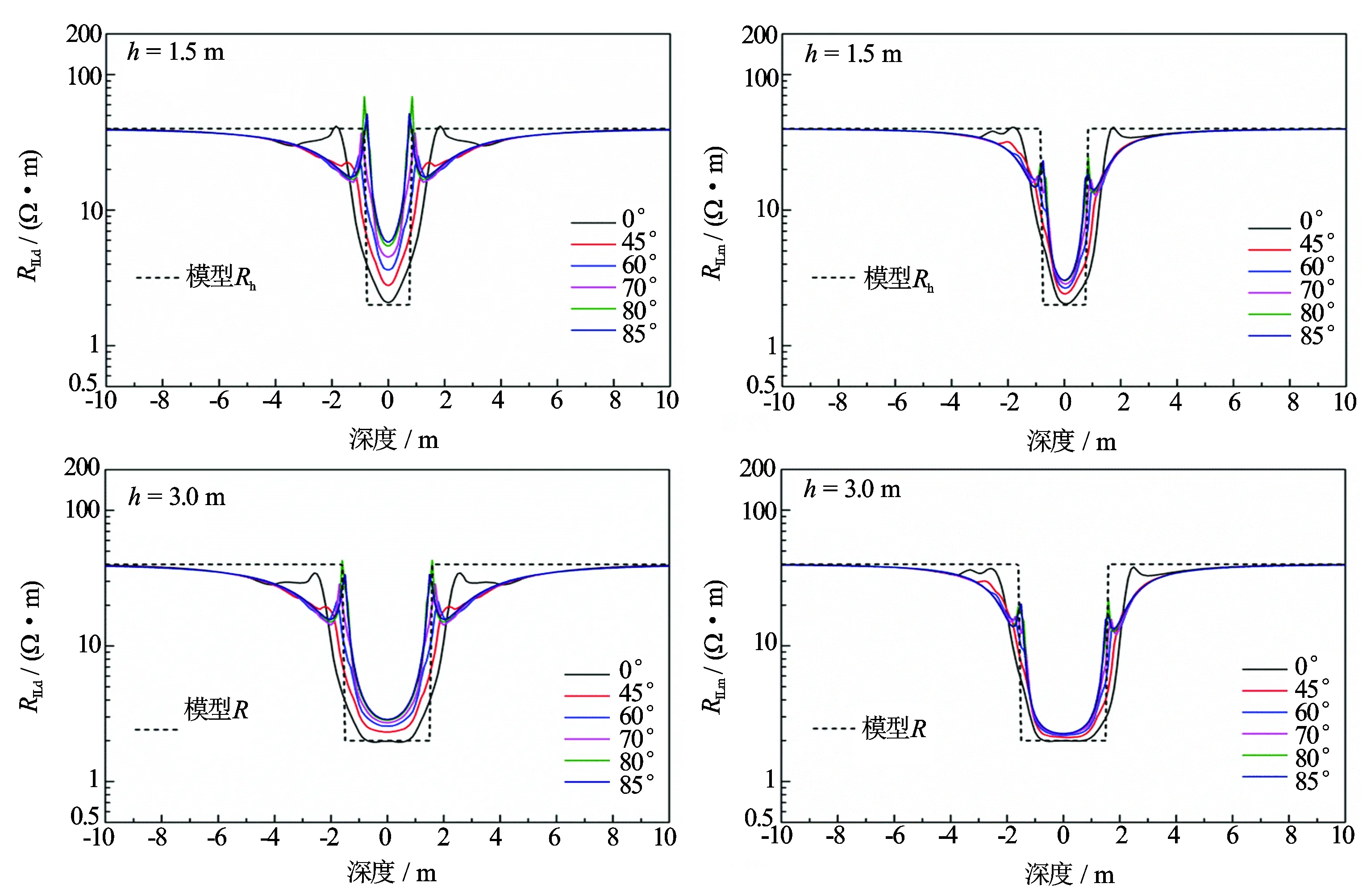
图7 层状各向同性地层中不同井斜角下深中感应测井响应

图8 层状各向异性介质中不同井斜角下深中感应测井响应

由图7可以看出,在层厚较小时,随着井斜角度的增大,目的层视电阻率增大,这是因为随着井斜角度的增大,双感应受围岩影响增大,视电阻率不断趋于围岩电阻率。而当目的层厚度较大时,围岩影响明显减弱。此外,由于深感应探测深度较深,受围岩影响较大,因此,深感应测井响应受井斜变化影响也较大。图8所示,不论目的层厚度大小,随着井斜角度的增大,目的视电阻率都迅速增大,表明井斜和各向异性对双感应测井响应的作用是相互影响的,响应结果较为复杂,对比图7,可以认为,在层厚较小时,应当优先考虑进行层厚校正,而当层厚较大时,必需进行各向异性校正。

3 双感应测井各向异性校正初探

大斜度井/水平井中随着井斜角度的增大,各向异性对双感应测井响应的影响显著增大,这为利用传统双感应测井进行地层各向异性评价提供了理论上的可能性。为此,通过制作双感应测井各向异性敏感性图进行双感应各向异性敏感性分析。

图9 双感应测井响应各向异性敏感性图

3.1 敏感性分析及校正图版

假设地层无限厚,不考虑围岩影响,则大斜度井/水平井中双感应只受地层各向异性影响。图9为不同地层电阻率下深中感应测井响应随各向异性系数变化。地层电阻率较低(小于10 Ω·m)、各向异性系数较大(大于2)时,深中感应测井响应对各向异性的敏感性出现较大差异,依此可利用深中感应测井响应的差异制作图版,进行各向异性评价,同时确定地层真实电阻率。

图10 双感应测井响应各向异性校正图版

图10为不同井斜角下双感应测井各向异性校正图版。依据井斜的大小,将深中感应视电阻率投影到图版中,可以得到地层的水平电阻率及地层各向异性系数。图10中随着井斜角度的减小,图版范围明显缩小,表明当井斜角度较小时双感应测井响应对各向异性不敏感,无法利用双感应数据进行各向异性校正。而从前文可知,当井斜角度较小时,双感应测井只能反映水平电阻率,无法通过双感应测井获取各向异性信息。

3.2 层状各向异性地层校正

大斜度井/水平井的校正不同于常规直井校正,各因素之间往往相互影响,因此,校正时应结合实际,考虑主要影响因素进行相应的校正。以图1所示模型,假设围岩电阻率为20 Ω·m,目的层水平电阻率为2 Ω·m,各向异性系数取1、2、3。

利用本文提供图版校正后,视电阻率值见表2。从表2可以看出,

经过校正的视电阻率值更加接近

目的层水平电阻率值。目的层为1.5 m,各向异性系数为3时,深感应视电阻率为13.25 Ω·m,校正后水平电阻率为1.1 Ω·m,误差值减小了517.5%;目的层厚度为5.5 m,各向异性系数为3时,深感应视电阻率为6.93 Ω·m,校正后水平电阻率为1.6 Ω·m,误差值减小了226.5%。可见,各向异性地层若不进行校正,会给测井解释评价带来巨大问题,而本文提供的校正方法可大大减小误差。另一方面,层厚为1.5 m,各向异性系数为3时,校正后电阻率误差为45%,而层厚为5.5 m,各向异性系数为3时,校正后电阻率误差下降到了20%。可见,目的层厚度较大时(大于5 m),进行各向异性校正具有较好的效果,而层厚较小时(小于5 m),应当优先考虑进行层厚校正。

表2 校正后目的层水平电阻率

此外,对比表1和表2,各向异性系数为1(各向同性),目的层厚度较大时,校正后水平电阻率与测量值相比误差增大,这也说明了大斜度井中层厚、井斜与各向异性共同作用的复杂性。在应用中,应当结合实际测井环境,根据主要影响因素进行相应的校正。

4 结 论

(1) 直井条件下双感应测井只能反映地层水平电阻率,斜井时响应是水平电阻率和垂直电阻率的综合作用的结果,随着井斜角度的增大双感应测井值由水平电阻率向垂直电阻率过渡。

(2) 井斜角度及地层电阻率对比度越大、各向异性强,双感应测井响应在地层界面处的“犄角”幅度及范围越大。

(3) 直井中,双感应测井响应不受地层各向异性影响,随着井斜角度的增大,地层各向异性对双感应测井响应影响增大,双感应测井响应对各向异性识别能力增强。深感应测井响应对各向异性的敏感性大于中感应测井响应,据此利用深中感应测量值制作不同井斜下的各向异性校正图版进行校正。

(4) 大斜度井/水平井中,当目的层厚度小于5 m时应该优先考虑层厚校正;当目的层厚度大于5 m时应当进行各向异性校正。本文提供的各向异性校正图版适用于目的层厚度较大,各向异性较强的地层。

参考文献:

[1] James D Klein. Induction Log Anisotropy Corrections [J]. The Log Analyst, 1993, 34(2): 18-27.

[2] 汪宏年, 杨善德, 王艳. 各向异性地层中电阻率测井的响应特征 [J]. 石油地球物理勘探, 1999, 34(6): 649-657.

[3] 高杰, 谢然红. 大斜度井侧向测井三维正演数值模拟及曲线快速校正方法研究 [J]. 石油勘探与开发, 2000, 27(2): 69-71.

[4] 邓少贵, 仝兆岐, 范宜仁. 各向异性倾斜地层双侧向测井响应数值模拟 [J]. 石油学报, 2006, 27(3): 61-64.

[5] 范宜仁, 李虎, 胡云云, 等. 倾斜各向异性地层随钻电磁波响应模拟 [J]. 电波科学学报, 2013, 28(5): 994-998.

[6] Hardman R H, Shen L C. Theory of Induction Sonde in Dipping Beds [J]. Geophysics, 1986, 51(3): 800-809.

[7] Hardman R H, Shen L C. Charts for Correcting Effects of Formation Dip and Hole Deviation on Induction Logs [J]. The Log Analyst, 1987, 28(4): 349-356.

[8] Barbara Anderson, Kambiz Ali Safinya, Tarek Habashy. Effect of Dipping Beds on the Response of Induction Tools [J]. SPE Formation Evaluation, 1988, 3(1): 29-36.

[9] 肖加奇, 张庚骥. 水平井和大斜度井中的感应测井响应计算 [J]. 地球物理学报, 1995, 38(3): 396-404.

[10] 高杰, 柯式镇, 魏宝君, 等. 电法测井数值模拟现状及发展趋势分析 [J]. 测井技术, 2010, 34(1): 1-5.

[11] Anderson B I, Barber T D, Luling M G. The Response of Induction Tools to Dipping, Anisotropic Formations [C]∥SPWLA 36th Annual Logging Symposium, Paris, France, 1995.

[12] 胡松, 周灿灿, 王昌学, 等. 水平井各向异性地层双感应测井响应数值模拟 [J]. 科学技术与工程, 2014, 14(11): 10-13.

[13] Lili Zhong, Jing Li, Ashutosh Bhardwaj, et al. Computation of Triaxial Induction Logging Tools in Layered Anisotropic Dipping Formations [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(4): 1148-1163.

[14] Moran J H, Kunz K S. Basic Theory of Induction Logging and Application to Study of Two-coil Sondes [J]. Geophysics, 1962, 27(6): 829-858.

[15] 张庚骥. 电法测井 [M]. 东营: 中国石油大学出版社, 2003: 148-155.

[16] Shen L C. Effects of Skin-effect Correction and Three-point Deconvolution on Induction Logs [C]∥SPWLA 29th Annual Logging Symposium, San Antonio, Texas, 1988.

[17] 仵杰, 龚厚生, 陈草堂. 双感应测井趋肤效应校正和刻度系数计算研究 [J]. 测井技术, 2001, 25(4): 261-265.

[18] 魏宝君. 感应测井趋肤效应校正的迭代方法 [J]. 测井技术, 2004, 28(5): 367-372.

[19] 朱军, 李西钢, 夏克文, 等. 感应测井中的相位移误差 [J]. 测井技术, 1994, 18(4): 248-254.