高职教育质量评价方法的比较研究

董海茵，赵银善，马国泰，张　弟

(新疆农业职业技术学院，新疆 昌吉 831100)



高职教育质量评价方法的比较研究

董海茵，赵银善，马国泰，张弟

(新疆农业职业技术学院，新疆 昌吉 831100)

摘要：通过对高职教育质量评价体系评价方法及其应用的研究，论述了层次分析法、模糊综合评判法、灰色关联度法、主成分分析法的基本理念和应用步骤，对比分析了各类方法的优缺点.指出根据评价的目标特性，应选用客观有效和操作性强的评价方法，或是采用两种以上的方法，从而提取更有价值的信息，提高评价体系的质量和可信度.

关键词：高职教育;质量评价;数学方法

随着职业教育不断的改革，发展方式由外延式向内涵式全面转变，高职教育面临着规模和质量的博弈，而提高教育教学质量的有效保障就是开展质量评价，这也是促进高职院校内涵式发展的一项重要举措.各高职院校结合自身的特点，制定了教学、管理等质量评价体系，以期在教学质量、人才培养、专业建设等方面起到管理与监督作用.而提高评价体系的质量和可信度，需要选择科学、有效的技术和数学方法，使研究成果更加切合实际,进一步完善教育质量监控和评价体系.

通过对国内外文献的研究，现对几种常用的数学方法进行介绍.

1层次分析方法

层次分析法(AHP)是定性分析和定量分析相结合，处理多层次、多目标问题的决策方法，该方法结合了人的主观判断，应用简洁灵活，系统性强[1].

1.1主要步骤

(1)建立递阶层次结构模型

先将复杂问题所涉及的因素条理化，分成若干层次，建立多级递阶的层次结构模型(目标层、准则层、因素层)，根据问题的复杂程度和涉及的影响因素进行分层，层数不受限制.但通常情况下，每一层次中各指标支配的元素应小于9.

(2)构建各层次中的判断矩阵

准则层各项指标在目标决策中所占的重要程度是不相同的，可由同层次指标进行对比，判断比较任意两个因素之间的重要性，并给予量化(引用1-9及其倒数作为标度，见表1)，按两两比较结果构成的矩阵称作判断矩阵A=(aij)n×n.

表1　1-9标度及含义

构建判断矩阵应科学公正，可以通过合理设计调查问卷，得到需要的数据.

(3)计算权重

通过计算判断矩阵的权重，可以从中获取所需信息，为相关决策提供科学合理的依据，即需要得到最大特征值所对应的特征向量，进行归一化处理作为权值.

(4)一致性检验

在实际中，若出现不合常理的判断“A比B重要，B比C重要，而C又比A重要”，会导致评价失真，所以需要对判断矩阵进行一致性检验.当一致性比率CR<0.1，则判断通过一致性检验，同时不允许偏离一致性过大.未通过一致性检验的判断矩阵还需对原始数据进行合理修正，使其通过一致性检验.

1.2优点

(1)定性分析与定量分析相结合，分析决策过程条理性、科学性强.

(2)能较好分析解决复杂的决策问题，原理简单，评价结果可靠性强，误差小.

1.3缺点

(1)因专家的主观判断存在认识上的模糊性，会导致评价过程带有主观色彩，降低决策结果的可信度.

(2)判断矩阵会出现不能通过一致性检验的情况.

2模糊综合评判法

模糊综合评判法是运用模糊数学的基本理论和方法，对各个领域中存在的模糊不确定的复杂现象进行量化，进而做出相对客观、符合实际的综合评价方法.

2.1具体步骤

(1)建立评价指标体系

分析相关问题，确定影响总体评价目标的因素,需要对各级评价因素进行分析比较,找出主要因素,再将评价目标与实际状况进行比较,做出决策判断.指标体系可以分为目标层、准则层、统计指标层.

(2)构建评价的指标因素集U

评价指标体系要求各指标之间的支配关系应以上一层次的元素作为准则对下一层次有关元素起支配作用的层次结构形式来表达[2].那么,归属同一层次指标的下一层次各因素就可以组成一个因素集U={u1,u2,u3,…un}.

(3)确定评判的评语集V

评语集是对因素进行评价得到的结果所组成的集合，不论因素如何分类，评语集是唯一的，可设为V={v1,v2,v3,…,vm}，其中，vj(j=1,2,…,n)表示由高到底的各级评语，根据需要评价标准可进行等级划分(三级、四级等).如三级评语可设为“优秀、合格、残次”.

(4)确定因素集的模糊评价矩阵R

(5)构造判断矩阵计算权重集

在这里，一般釆用层次分析法确定各因素和因素集的权重，尽可能地降低人为因素的影响.在因素集中,通过对其所支配的因素进行任意两因素间重要程度的比较，形成判断矩阵，计算对应的权重集，就可以将权重分配设为U上的模糊集.

X=(x1,x2,…,xn)式中xi为第i因素的权重.且∑xn=1.

(6)模糊综合评价模型

由组合(U,V,R)，得到模糊综合评价模型Y=X*R，其中Y=(y1,y2,…,yn)为V上的模糊集, 式中yj(j=1,2,…,n)表示第j种评语在总体评价V中占有的比例.

(7)计算模糊综合评价结果

①加权平均计算法：以权重为基础,所有因素参与运算.

yj=(x1*r1j)⊕(x2*r2j)⊕(x3*r3j)⊕…⊕(xn*rnj)，(j=1,2,…,m)

②主因素决定法：计算中即注重主因素，也注重单因素的决策作用.

③主因素突出法：类似于方法②，但更深入.在重点分析主要因素的同时,考虑非主要因素的影响.

yj=(x1∧r1j)⊕(x2∧r2j)⊕(x3∧r3j)⊕…⊕(xn∧rnj)，(j=1,2,…,m)

2.2优点

(1)定性方法和定量方法相结合，评价过程使不确定现象和模糊事物之间的差异得以量化，即定性指标定量化，从而解决问题.

(2)对所需的数据要求低，模型运算结果为一向量，计算量不大.

2.3缺点

(1)忽略评价指标的相关性，出现评价信息重复.

(2)由层次分析法获得因素权重，评价过程存在主观臆断.

(3)在多目标评价模型中，隶属函数的确定有一定困难.

3主成分分析法

主成分分析(PAC)是将多指标转化为几个互不相关的综合指标,且尽可能反映原来所有指标的信息量，以达到简化数据、降低维度的多元统计方法.

3.1具体步骤

(1)构建样本矩阵

假设某一多目标决策问题有n个评价单元，每个单元有p个评价指标(变量)：X1,X2,…,XP,每个评价对象对应不同评价指标的取值xij,即为样本矩阵:

X=(xij)n×p=(X1,X2,…,XP)

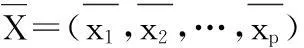
则X的第i个主成分为Fi=aiX,(i=1,2,…,p)

(4)求出n个样本在r个主成分上的得分:

Fi=a1iX1+a2iX2+…+apiXp，(i=1,2,…,r)

由得分进行样本排序，得到综合评价结果.

3.2优点

(1)主成分因子的选择确定，精简了原指标数量.

(2)评价因子的权重是由累计贡献率来确定的，避免主观因素的存在，客观科学合理.

3.3缺点

(1)样本数量较大，会造成运算繁琐.

(2)样本量的规模会影响评价的结果.

(3)指标间会存在信息重叠问题，有可能导致评价结果出现偏差.

4灰色关联度分析法

灰色关联度分析是当事物运行机制不清晰或者数据不明确的情况下，对既有信息进行处理，利用灰色关联度使因素间的关系量化和次序化，从而进行整体比较[3].

4.1具体步骤

(1)构建评价指标矩阵

在进行灰关联分析时, 首先是进行评价指标的选择,由专家评分可以构造评价指标矩阵.假设现有m个待评价单元,每个单元有n个评价指标, 通过专家对待评价指标进行评分,构造m×n阶评价指标矩阵: X=(xij)m×n，其中xij为第i个评价单元在第j个评价指标下的值.

(2)确立标准模式

标准模式即为评价指标矩阵的最优效果向量X0,即为:

在上述矩阵中加入向量X0,进而可以构造(m+1)×n阶评价指标矩阵:

X=(xij)(m+1)×n

(3)灰靶变换

进行灰靶变换,把数据差异较大的各项指标,进行规范化处理,使指标具有可比性.采用变换方法:

经过处理， 原评价指标矩阵X=(xij)(m+1)×n转化为T=(tij)(m+1)×n，标准模式转化为标准靶心为:X0=(1,1,1,…,1,1,1)

(4)计算两极差

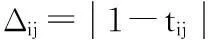
(5)构造靶心系数矩阵

差异信息空间的每一个单元与靶心的灰关联度,即靶心度, 其几何含义为待评单元与靶心的相距程度,两者距离越近,靶心度越大,评价单元越优；反之, 评价单元欠佳.

将xij与x0j在第j个指标上的靶心系数记作ξ0i(j)，则有:

再以ξ0i(j)为因素可以构造靶心系数矩阵ξ0i(j)m×n.

(6)单元评价

比较靶心度大小，对评价单元进行排序，靶心度越大，评价单元越优.

4.2优点

(1)该方法可用原始数据直接计算，易于掌握，计算量小，结果客观可信.

(2)对数据要求不高，数据较少或是不具有明显的分布规律，也可以进行计算.

4.3缺点

(1)比较序列、分辨系数等的取值不同会影响评价单元，导致结果不唯一.

(2)事物间既可能是正相关，也会有负相关，当存在负相关关系时采用关联度模型，会得出错误的结论.

(3)该方法不适用于评价指标信息重复的情况，所以指标的选择对评价结果有很大的影响.

总之，对教学、管理等质量评价体系进行统计分析的数学方法众多，必须根据评价的目标特性，考虑每种方法的侧重点，选择客观有效和操作性强的评价方法，或是采用两种以上的评价方法，从数据中提取更有价值的信息，使研究结果更加切合实际，从而提高评价体系的质量和可信度.

参考文献：

[1]李丁,韩伟一,汪云林.关于层次分析法的数值试验[J].统计与信息论坛,2013,(2):10-14.

[2]王丽娜.基于ISO9000的高职会计专业教学质量评价体系研究[D].长沙:中南大学硕士学位论文,2012.

[3]方刚.基于灰关联分析的教学质量评价模型及应用[J].广东技术师范学院学报,2008,(9):52-54.

(责任编校：晴川)

Comparative Study on Quality Evaluation Methods of Higher Vocational Education

DONG Haiyin，ZHAO Yinshan，MA Guotai，ZHANG Di

(Xinjiang Agricultural Vocational Technical College, Changji Xinjiang 831100, China)

Abstract：Through researching the methods of quality evaluation system of higher vocational education and their applications, the paper discusses the basic concepts and application steps of AHP, FCE, PCA and GRA, and comparatively analyzes the advantages and disadvantages of these methods. It is pointed out that based on the target characteristics of the evaluation, objective and effective evaluation method with good operational performance should be selected, or two methods and even more than two kinds of methods should be used in order to extract more valuable information and improve the quality and credibility of the evaluation system.

Key Words：higher vocational education; quality evaluation; mathematical method

中图分类号:G717

文献标识码：A

文章编号：1008-4681(2016)02-0136-04

作者简介：董海茵(1979— )，女，湖北鄂州人，新疆农业职业技术学院副教授，硕士.研究方向：数理金融与保险精算.

基金项目：新疆维吾尔自治区高校科研计划青年项目(批准号：XJEDU2014S085);新疆农业职业技术学院重点课题(批准号：XJNZYSK2014006 );新疆农业职业技术学院一般课题(批准号：XJNZYSK201520).

收稿日期：2015-10-04