关于非阿基米德域上广义费马型函数方程

亓金锋

(山东广播电视大学公共基础教学部，山东 济南 250014)



关于非阿基米德域上广义费马型函数方程

亓金锋

(山东广播电视大学公共基础教学部，山东 济南 250014)

摘要：利用亚纯函数值分布理论的基本概念、方法及研究成果，给出了非阿基米德域上广义费马型函数方程存在非常数亚纯解f1,f2,...,fp 的一个必要条件：，其中， T(r,ai)=o(T(r,fi)),1≤i≤p，r→∞(r∉E).该结论改进了Hu和Yang的相关研究结果.

关键词：亚纯函数；非阿基米德域；费马型函数方程

本文使用 Nevanlinna 理论的基本结果及其标准记号，参看[1]或[2].我们主要讨论具有如下形式的函数方程：

(1)

其中当r→∞(r∉E) 时，

T(r,ai)=o(T(r,fi)),1≤i≤p，是一个线性测度为有穷的集合，我们称上述方程为广义费马型函数方程.特别地，如果(1)式中所有函数ai(z)都是1以及所有整数ni都相等，那么我们称之为费马型函数方程.

1969年，Yang[3]在复数域上研究了一类特殊函数方程，证明了如下结果：

T(r,a)=o(T(r,f)),T(r,b)=o(T(r,g)),

那么函数方程

a(z)fm(z)+b(z)gn(z)≡1不可能成立，除非m=n=3.如果f与g是整函数，即使满足m=n=3，该函数方程也不成立.

1970年，Toda N[4]考虑了p(p≥2)个整函数解的情况，事实上研究了广义费马型函数方程(1)存在整函数解的必要条件，得到了定理B.

定理B设f1,f2,…,fp(p≥2)是上的p个非常数整函数，n1,n2,…,np是正整数，a1,a2,…,ap是上的不恒为零的亚纯函数，且满足当时，T(r,ai)=o(T(r,fi)),1≤i≤p.如果函数方程(1.1)成立，则.

一个自然的问题：函数方程(1)对于亚纯函数解是否存在类似的结论？2002年，Yu和Yang[5]将定理B中的整函数推广至亚纯函数，证明了定理C.

定理C 设f1,f2,…,fp(p≥2)是上的p个非常数亚纯函数，n1,n2,…,np是正整数，a1,a2,…,ap是上的不恒为零的亚纯函数，且满足当时，T(r,ai)=o(T(r,fi)),1≤i≤p.如果函数方程(1)成立， 则.

近年来，国内外许多学者对在数论占重要地位的非阿基米德域上的Nevanlinna理论的产生了兴趣，并取得了一系列结果.事实上在非阿基米德域和复数域上的值分布论不是孤立的，而是互相联系的，因此把这两种不同域上的值分布问题放到一起来进行研究就很有意义.Hu和Yang[6]在非阿基米德域上研究此类费马型函数方程解的存在情况，得到了下述定理D和定理E.

定理D ([6], p65,定理2.41) 设f1,f2,…,fp(p≥3)是k上的p个非常数亚纯函数，n1,n2,…,np是正整数，如果函数方程

f1n1+ f2n2+ … + fpnp= 1

成立，则

其中

(2)

定理E ([6], p65,定理2.42] 设f1,f2,…,fp(p≥3)是k上的p个非常数亚纯函数，如果

n≥p(p-1+ϑp)，

其中由(2)式定义，则函数方程

不存在非常数亚纯解.

本文我们把定理D、定理E中函数方程的系数由常数1推广为p-adic亚纯小函数，证明了定理1和定理2.

定理1设f1,f2,…,fp(p≥3)是k上的p个非常数亚纯函数，n1,n2,…,np是正整数，a1,a2,…,ap是k上的不恒为零的亚纯函数，且满足当r→∞(r∉E)时

T(r,ai)=o(T(r,fi)),1≤i≤p.

如果函数方程(1)成立， 则

定理2设f1,f2,…,fp(p≥3)是k上的p个非常数亚纯函数，n1,n2,…,np是正整数，a1,a2,…,ap是k上的不恒为零的亚纯函数，且满足当r→∞(r∉E)时

T(r,ai)=o(T(r,fi)),1≤i≤p.

如果

n≥p(2p-3)，

其中由(2)式定义，则函数方程

不存在非常数亚纯解.

1相关引理

首先，我们定义的极点的计数函数Np-1(r,f)，其中极点重级至多为p-1时，按重数计算；极点重级大于p-1时，计p-1次.由这个定义出发，我们可以得到引理1和引理2.

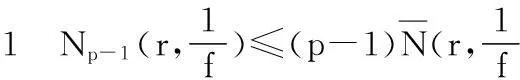
引理2[6]设(p≥2)是正整数，f1,f2,…,fp是k上线性无关的非常数亚纯函数且满足

f1+f2+…+fp=1

则对于1≤j≤p，有如下不等式成立

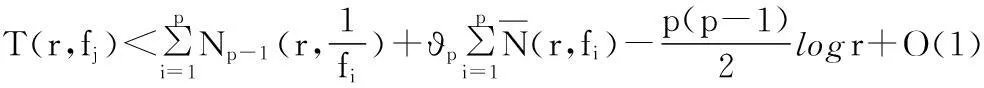
(3)

其中ϑp由(2)式定义.

由引理1以及引理2中的(3)式子，我们得到引理3.

引理3 在引理2 的条件下，我们有如下不等式

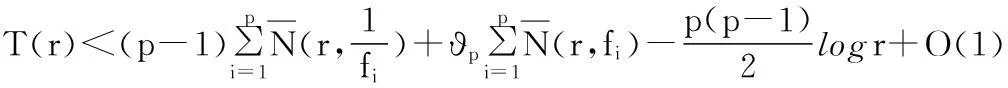
(4)

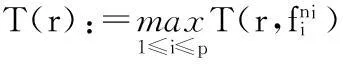
引理5[6]设f为k上非常数亚纯函数，如果满足T(r,f)-O(logr)(r→∞)，则f是有理函数.

2定理证明

2.1定理1的证明

下面我们将分两种情形进行讨论.

情形1F1,F2,…,Fp线性无关.

由第一基本定理得

(5)

和

(6)

对于引理中3的(2)式运用数学归纳法易得，结合(5)式、(6)式得

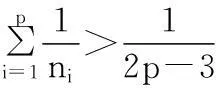
情形2F1,F2,…,Fp线性相关.

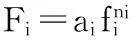
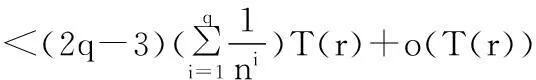
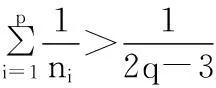
2.2定理2的证明

由定理1的逆否命题可得，设f1,f2,…,fp是k上的p个非常数亚纯函数，n1,n2,…,np是正整数，a1,a2,…,ap是k上的不恒为零的亚纯函数，且满足当r→∞(r∉E)时，

T(r,ai)=o(T(r,fi)),1≤i≤p.

如果

(7)

方程(1)

a1f1n1+ a2f2n2+ … + apfpnp= 1

(8)

不存在亚纯解.

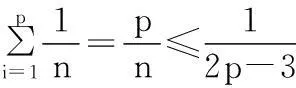
这样就得到了定理2中的函数方程，从而完成了定理2的证明.

参考文献：

[1]Hayman W K. Meromorphic Functions [M]. Oxford: Clarendon, 1964.

[2]Yang C C, Yi H X. Uniqueness Theory of Meromorphic Functions [M]. Science Press/ Kluwer Academic Publishers, 2003.

[3]Yang C C. A generalization of a theorem of P Montel on entire functions [J].Proc Amer Math Soc, 1970, (2):332-334.

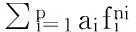
[5]Yu K W, Yang C C. A note for Waring’s type of problem for the ring of meromorphicfunctions [J]. Indian J Pure Appl Math, 2002,(10):1495-1502.

[6]Hu P C, Yang C C. Meromorphic Functions over Non-Archimedean Fields [M]. The Netherlands: Kluwer Academic Publishers, 2000.

(责任编校：晴川)

On Generalized Fermat Type Functional Equations over Non-Archimedean Fields

QI Jinfeng

(Department of Public Basic Teaching, Shandong TV University, Ji’nan Shandong 250014, China)

Abstract：By using some fundamental knowledge, research methods and research results about the theories of value distribution for meromorphic functions, it shows that a necessary condition for the generalized Fermat type functional (z)≡1(p≥2)having non-constant meromorphic solutions f1,f2,…,fp，where T(r,ai)=o(T(r,fi)),1≤i≤p，r→∞(r∉E). This improves the study results of Hu and Yang.

Key Words：meromorphic functions; non-Archimedean field; Fermat type functional equations

中图分类号:O174.5

文献标识码：A

文章编号：1008-4681(2016)02-0001-03

作者简介：亓金锋(1984— )，男，山东临沂人，山东广播电视大学公共基础教学部讲师，硕士.研究方向：复分析.

基金项目：山东省职业教育与成人教育科研规划课题(批准号：2014ZCJ008);山东广播电视大学青年教师科研项目(批准号：2014QNYJ06).

收稿日期：2015-12-30