主动配电网三相解耦潮流算法

杨 雄卫志农孙国强孙永辉杨永标陈 璐

（1.河海大学能源与电气学院 南京 210098 2.江苏省电力公司电力科学研究院 南京 211103 3.国电南瑞科技股份有限公司 南京 211106）



主动配电网三相解耦潮流算法

杨 雄1,2卫志农1孙国强1孙永辉1杨永标3陈 璐3

（1.河海大学能源与电气学院 南京 210098 2.江苏省电力公司电力科学研究院 南京 211103 3.国电南瑞科技股份有限公司 南京 211106）

摘要随着主动配电网技术迅速发展，分布式电源（DG）规模化接入，传统配电网潮流算法难以满足主动配电网潮流计算的要求。针对这一情况，提出一种能高效处理多类型DG规模化接入和环网的主动配电网三相解耦潮流算法。该算法基于序分量法和不对称线路三序解耦-补偿模型，结合主动配电网的特点和道路-回路分析法，详细推导PQ、PQ（V）、PV和PI节点类型DG规模化并网和无功补偿设备接入的潮流模型，采用三相解耦及并行计算，极大地提高算法计算速度和效率，节省内存空间，实现高效的主动配电网三相解耦潮流计算。通过IEEE 37、69和123母线测试系统验证了该算法的有效性、良好的收敛性以及较强的处理多类型DG规模化接入和环网的能力，且算法性能远优于传统算法。

关键词：主动配电网 三相解耦 潮流计算 环网 分布式电源 三相不平衡 无功补偿

国家电网公司科技项目（智能配用电的技术体系及仿真基础性问题研究），国家自然科学基金（51277052、51107032和61104045）和江苏省普通高校研究生科研创新计划（CXZZ13_0238）资助项目。

0 引言

主动配电网潮流计算是主动配电系统分析的一项重要内容，是对主动配电系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的重要依据。一方面，主动配电网一般是环形设计、闭环运行，在规划设计和运行分析计算时，需要计算闭环运行的弱环主动配电网三相潮流；另一方面，随着主动配电网技术和分布式发电技术迅速发展，越来越多分布式电源（Distributed Generation，DG）规模化接入配电网，给配电网的网络结构、功率损耗、电压分布和潮流计算产生了巨大的影响[1-6]，而且主动配电网技术对三相潮流计算的性能提出了更高的要求。因此，研究适合主动配电网发展要求的主动配电网三相潮流计算方法是非常必要的。

到目前为止，国内外学者已经进行了大量含DG的配电网潮流算法研究[7,8]，提出了很多算法。文献[9]提出了基于灵敏度补偿的配电网潮流计算方法，具有高效的DG处理能力。文献[10]提出了改进节点关联矩阵自乘的配电网潮流算法，对PV节点采用无功功率分摊原理的初值确定法，提高了算法的收敛速度。文献[11]提出了含DG的基于网损灵敏度的配电网潮流算法，效率较高，但处理PV节点较麻烦。文献[12]提出了一种改进前推回代法，研究了各种类型DG在改进前推回代算法中的计算模型，但文献[9-12]均未计及配电网的三相不平衡情况和环网。文献[13]基于网络层次矩阵快速前推回代计算含DG的配电网潮流，但在处理PV节点时，收敛速度变慢，迭代次数剧增，且未计及三相不平衡情况。文献[14]提出了基于牛顿法的能够处理各种DG的配电网三相潮流计算方法。文献[15]采用一种改进牛顿-拉夫逊法来计算含DG的配电网三相潮流。文献[16]提出了基于分布式松弛母线模型的含DG三相不平衡潮流计算，但计算过程复杂。文献[17]基于前推回代法，提出了可处理PV和PQ节点模型DG的三相不平衡潮流计算，利用支路分层技术加快了潮流计算速度，但文献[15-17]均未考虑环网问题。文献[18]基于正序分量推导了一种求解PV节点无功功率增量计算的新方法，并将其引入到弱环配电网三相潮流算法中，处理回路能力较强，但仅考虑了PV节点类型DG。文献[19]基于改进前推回代法提出了适用于含多种DG的弱环配电网三相潮流算法，取得了较好的效果，但PV节点和环网增多时，计算效率会显著降低。

因此，本文提出了一种能高效处理多类型DG规模化接入和环网的主动配电网三相解耦潮流计算方法。该方法首先基于序分量法[20,21]和不对称线路三序解耦-补偿模型[22]，结合主动配电网的特点和道路-回路分析法，详细地推导了PQ、PQ（V）、PV 和PI节点类型DG规模化并网和无功补偿设备接入的潮流计算模型；然后，实现了一种高效的主动配电网三相解耦潮流算法；最后，利用IEEE 37、69 和123母线测试系统验证了该算法的有效性和良好的收敛性。

1 主动配电网三相解耦潮流算法

针对具有N个节点、b条支路和l个独立回路的三相主动配电网，假设首节点（根节点）是电源且作为参考节点，则独立节点个数为n＝ N-1，支路条数b＝ n＋ l。其中，树支n条，连支l条。

对于连通图中一棵选定的树，由于基本回路中仅包含一条连支，基本回路数等于连支数，基本回路-支路（下面简称“回-支”）关联矩阵B描述基本回路、树支和连支之间的联系[23]。其中回-支关联矩阵B是一个l× b阶矩阵，假定连支支路的正方向都是从大号节点指向小号节点，基本回路的正方向与连支支路的正方向相同，如果支路r在回路j上，且二者方向相同，则B（ j,r）＝1，如果支路r在回路j上，且二者方向相反，则B（ j,r）＝-1，如果支路r不在回路j上，则B（ j,r）＝0。

一个节点的道路是指节点沿树到根所经过的路径上的支路集合，节点的道路强调的是路径上的支路，对于一个给定的树，节点的道路是唯一的、只由树支组成，可用道路矩阵T描述[23]。其中道路矩阵T是一个n× b阶矩阵，假定道路的正方向都是从电源点（即根节点）指向各节点，各树支支路正方向与道路正方向相同，如果支路r在道路i上，则T（ i,r）＝1，反之T（ i,r）＝0。道路矩阵T是一个稀疏矩阵，利用稀疏技术可以降低内存需求。

在主动配电序网络中，定义节点注入序电流向量矩阵为Is,n（n×1阶），支路序电流向量矩阵为Is,b（b×1阶），连支序电流（也即回路序电流）向量矩阵为Is,（ll×1阶）。在三序解耦的各序网络电路模型中，可以获得各序网络的道路矩阵和回-支关联矩阵分别为T0、T1、T2和B0、B1、B2，并依据KCL电流定律，支路序电流Is,b、节点注入序电流Is,n和回路序电流Is,l满足等式

式中，下标s ＝0,1,2，分别表示序网络模型中的零序、正序和负序网络。

对任一主动配电网序分量电路模型中，基于欧姆定律，支路特性约束为

依据KVL电压定律，基本回路约束为

式中，Us,b为主动配电网支路序电压矩阵（b×1阶）；Zs,b为基于支路i的序阻抗Zs,bi形成的对角阵（n× n阶）；下标s＝0,1,2，分别表示序网络模型中的零序、正序和负序网络。

由式（1）和式（2）代入式（3）可得

式中，Zs,l为回路序阻抗矩阵，令其逆矩阵为Ys,l，则有

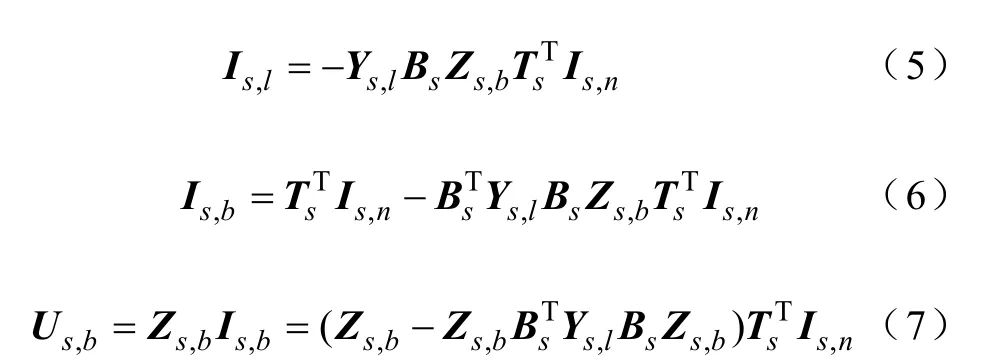
设电源节点三相电压相量矩阵为Uabc,0（3×1阶），各节点三相电压相量矩阵为Uabc,n（3n× 1阶），则可以得出电源节点的三序电压相量矩阵为U012,0＝AUabc,0（3×1阶），各节点三序电压相量矩阵为U012,n（3n× 1阶），那么，在各序网络模型中，可知任一节点与电源节点的序电压差等于从此节点开始沿着该节点的道路到达电源节点所经支路的支路序电压之和，设为n维向量；，则

式（8）是本文潮流算法计算的核心，潮流计算步骤如下（k为迭代次数）：

（4）依据文献[19]中的不对称线路三序解耦-补偿模型和两端节点补偿电流源计算公式，计算k次迭代时主动配电网中不对称线路两端节点补偿注入序电流

（7）依据式（9）计算k次迭代时的Us,nk。

2 各类型DG规模化并网的潮流计算模型

2.1 PQ节点类型DG

常规三相潮流计算中，PQ节点各相的注入有功和无功功率为给定值，对于三相不对称的负荷或功率源，这样的处理方式较合理。然而，传统含DG配电网三相潮流算法中均近似认为三相对称的PQ 型DG输出功率为给定值且三相功率对称相等，把其处理成三相功率对称相等的负荷。但三相对称DG接入三相不平衡主动配电网中，由于三相电压不对称，DG输出的三相功率并不对称相等，而且，考虑到发电机和三相对称的电力电子逆变器装置自身的运行特性[20,24]，对于三相不平衡的主动配电系统，传统方法中近似认为三相对称DG输出的三相功率对称相等且为给定值的处理方式就不够合理。针对这一问题，依据文献[20,24]，本文认为三相对称的PQ型DG输出恒定的有功功率和无功功率作为该DG节点注入系统的恒定正序有功功率和恒定正序无功功率，即

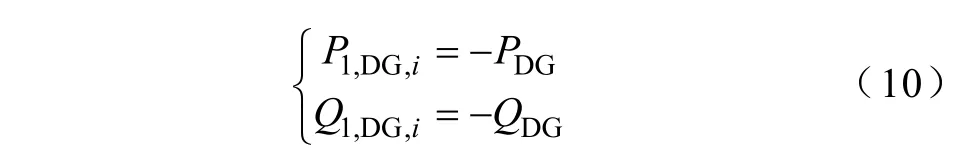
式中，PDG、QDG分别为三相对称的PQ型DG输出的恒定有功功率和恒定无功功率；分别表示第i个DG节点注入的正序有功功率和正序无功功率。

针对第i个PQ型DG节点，节点注入的正序电流可用式（11）计算。

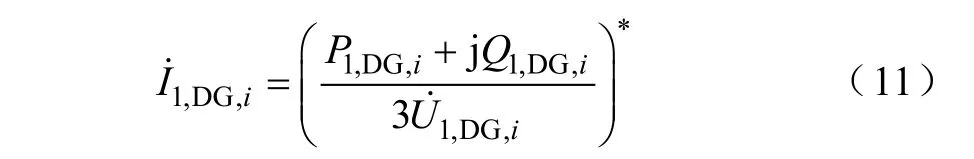
2.2 PQ（V）节点类型DG

该类型DG的处理方法类似于PQ节点类型DG的处理方法，其不同之处在于迭代过程中，需要根据最新PQ（V）节点类型DG的电压迭代值不断更新该DG注入系统的无功功率，然后将其代入式（11）求出该DG节点新的注入正序电流，并且开始下一次迭代。该类型DG节点注入的正序有功功率和正序无功功率计算模型分别为

式（12）取值有以下两种情况：

（1）采用无励磁调节能力的同步发电机作为接口时，DG发出的无功功率为

式中，PDG、EDGq、Xd和分别为DG机组的有功输出、空载电动势、同步电抗和机端电压幅值。

（2）采用异步发电机的风机作为接口时，DG吸收的无功功率为

考虑到异步发电机的风机作为接口的PQ（V）型DG接入主动配电网时会相应地安装无功补偿电容器设备，因此，设异步发电机的风机并网节点i处各相安装的无功补偿电容器设备参数为可以计算出则该DG节点安装的无功补偿电容器设备注入的各相电流为

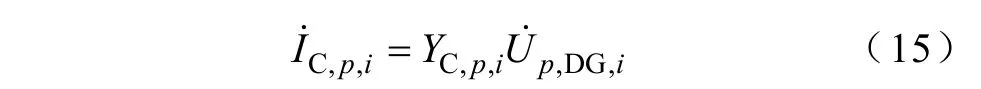
于是，该DG节点安装的无功补偿电容器设备注入的序电流为

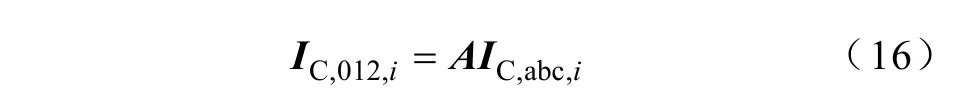
将无功补偿电容器设备注入的序电流叠加到该PQ（V）型DG节点注入的序电流中。

2.3 PV节点类型DG

考虑到发电机和三相对称的电力电子逆变器装置自身的运行特性[20,24]，以及三相对称DG接入三相不平衡的主动配电网中DG的三相电压不再对称，DG输出的三相功率也并不对称相等，本文认为三相对称的PV型DG输出恒定的有功功率作为该DG节点注入系统的恒定正序有功功率，其输出的额定电压作为该DG节点恒定的正序电压幅值，但是其输出的无功功率却是未知的。因此，问题的关键就是求出满足DG节点正序电压幅值与该PV 型DG额定电压值相等条件的该PV型DG输出的无功功率。

针对PV节点类型DG，可采用开环阻抗矩阵（即戴维南等效阻抗矩阵）来处理PV型DG节点，在一个含有个PV节点类型DG的三相主动配电网的正序网络中，若在每个PV型DG节点处开环后出现个开环点，则存在

针对任一主动配电网的正序网络中，从道路矩阵T1中把各PV型DG节点所对应行向量提取出来组成一个新的矩阵T1,DG，则有

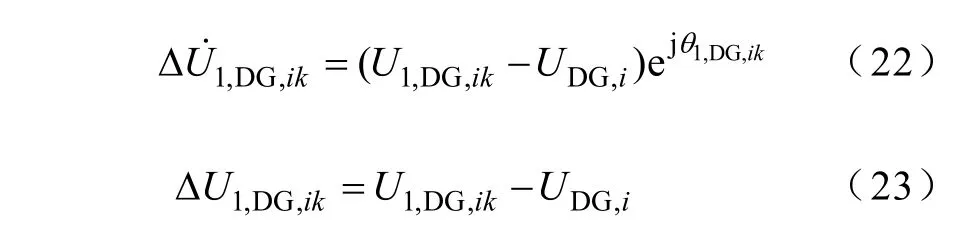
式中，UDG,i为第i个PV节点类型DG的额定电压值；的相角。

则该PV型DG节点正序有功功率的修正量为

因为PV型DG节点正序有功功率等于PV节点类型DG输出的恒定有功功率，即为常数，所以代入式（25）得

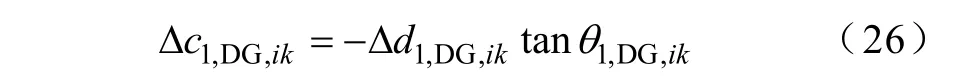
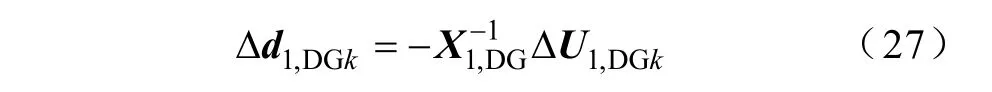
而该PV型DG节点正序无功功率的修正量为

把式（26）代入式（28）可得

第k1＋次迭代时，第i个PV型DG节点注入的正序无功功率为

然后将式（30）代入式（11）求出DG节点新的注入正序电流，开始下一次迭代。当满足收敛精度时，停止迭代。

2.4 PI节点类型DG

考虑到类似2.3节中的问题，本文认为三相对称的PI型DG输出恒定的有功功率作为该DG节点注入系统的恒定正序有功功率，其输出的额定电流作为该DG节点注入的恒定正序电流幅值。相应的DG输出的无功功率可按下式计算得出。

（1）迟相运行工况时

（2）进相运行工况时

式中，PDG为该DG输出的恒定有功功率；为该DG输出的额定电流；分别为第k次迭代时PI型DG节点i正序电压的实部和虚部。

因此，第k＋1次迭代时该PI型DG节点注入的正序无功功率为

并将式（33）代入式（11）求出该DG节点新的注入正序电流，开始下一次迭代。

在潮流迭代过程中，若PQ（V）、PV和PI型DG节点出现无功功率越界，则将其转换成PQ型DG节点处理，且QDG,1取各节点类型DG的无功上界或下界，然后重新计算。

另外，对于DG单相接入、两相接入或三相不对称DG接入的情况下，可以直接先按照各相分别进行计算，分别先求出DG各相注入电流，然后通过对称分量变换求出DG各序注入电流，便可容易将其叠加到DG节点注入的序电流中。

3 算例分析

3.1 算例1

参见文献[25]介绍的IEEE 37母线三相不平衡配电网，变压器Dd联结方式，增加五条环路，在母线12、25、29、30和35接入五个DG系统分别为DG-1、DG-2、DG-3、DG-4和DG-5，其单线图如图1所示。

图1　IEEE 37母线三相不平衡主动配电网Fig.1 IEEE 37-bus three-phase unbalanced active distribution network

在IEEE 37母线主动配电系统中，五个DG系统DG-1、DG-2、DG-3、DG-4和DG-5依次分别接入PQ、PQ（V）-1、PQ（V）-2、PV和PI节点类型DG系统，各节点类型DG并网参数见表1，其无功界限设置见表2。选择表3所示的七种运行方式进行分析讨论，七种运行方式潮流收敛后各节点A相电压幅值分布如图2所示，接入DG的无功越界及无功输出情况见表4，表5给出了以异步发电机的风机作为接口的PQ（V）型DG并网时无功补偿电容器设备输出的无功功率，另外，图3和图4分别给出了方式6和方式7中各DG输出的各相有功功率的比较结果。

表1　算例1中各节点类型DG并网参数Tab.1 The connected parameters of different node-types DG in test 1 　（标幺值）

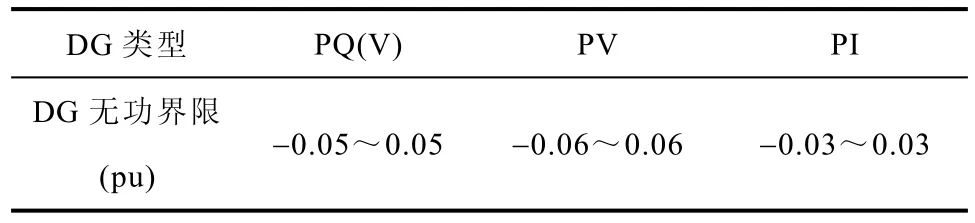
表2　算例1中各节点类型DG无功界限Tab.2 The reactive power boundaries of different node-types DG in test 1

表3　算例1的七种运行方式及潮流收敛迭代次数Tab.3 Seven modes and converged results of test 1

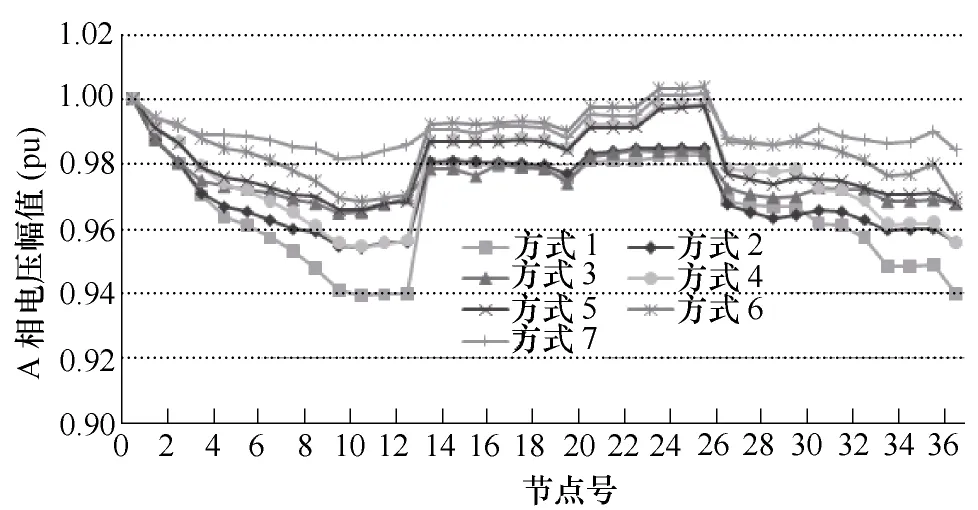
图2　算例1在七种运行方式下各节点A相电压幅值分布Fig.2 The node voltage profiles of phase A in seven modes of test 1

表4　算例1中DG的无功越界及无功输出情况Tab.4 Overstepped and outputted reactive power of the connected DGs in test 1

由表3可见，与其他方式相比，方式6和方式7中出现了迭代次数增加近似一倍，这是因为方式6和方式7中出现接入DG无功输出越界，潮流程序自动将无功越界DG转换成PQ型DG后重新进行潮流计算。另外，从表4中也可以看出在方式6和方式7中接入的PV型DG出现无功输出越界，而方式4和方式5中接入的DG均未出现无功输出越界。

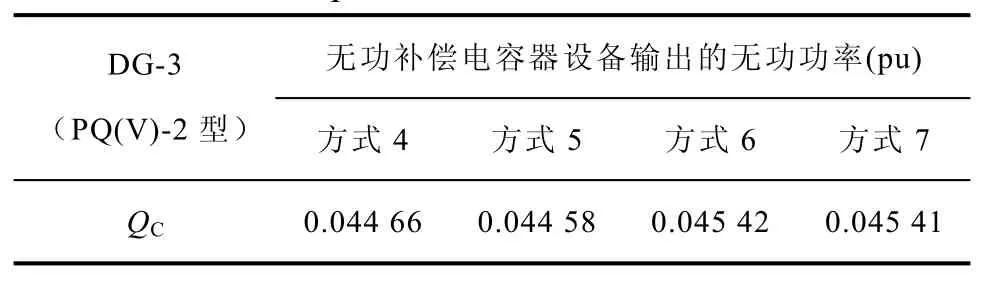
表5　方式4～方式7情况下无功补偿电容器设备输出的无功功率Tab.5 Outputs of the reactive power compensation capacitors in mode 4～7

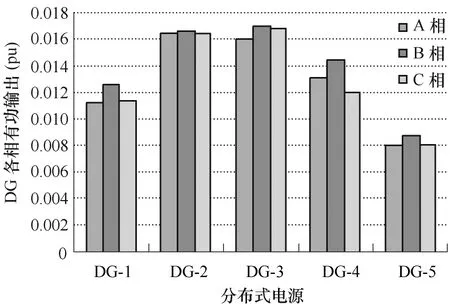
图3　算例1在方式6下各DG输出有功功率比较Fig.3 Comparison of DG’s active power in mode 6 of test 1

从表3和表4中可知，环路闭合后收敛次数减少，且随着闭合环路的增加潮流程序收敛性稳定；系统在接入DG及增加DG时，潮流的收敛性变化很小，但在DG出现无功越界时，迭代次数会有所增加，但并不影响潮流收敛。这些都显示了本文算法具有良好的收敛性和处理DG及环网能力。方式7和方式6分别在环状和辐射状主动配电网都同时接入了四种不同节点类型DG的情况下，潮流稳定收敛，表明了该算法具有较强的处理多种不同节点类型DG规模化并网和DG无功越界的能力。

由表4和表5可知，方式4～方式7中接入的以异步发电机风机作为接口的PQ（V）型DG-3，虽然该类型DG需要从主动配电系统中吸收无功功率，但是其安装的无功补偿电容器设备输出的无功功率都足以补偿该DG从主动配电系统中吸收的无功功率，且该DG向主动配电系统中输入了有功功率，因此，从图2可看出，相对于无DG接入的方式1～方式3来讲，该节点电压幅值都有提高。

由图2可看出，在方式1无环路闭合和无DG接入的情况下，系统的节点电压分布最差，随着环路闭合或DG接入后节点电压水平得到了改善。DG接入及其输入有功功率和无功功率，减少了系统线路上功率流动，从而改善了系统的电压水平；闭合环路虽然没有增加额外功率，但改变了系统的功率流向，缩短了负荷与电源之间的电气距离，负荷节点注入电流引起的支路电压降变小，对改善系统电压水平同样具有很好的效果。但总的来说，随着增加接入DG和闭合环路的数量，电压水平会得到更好的改善，如在方式7闭合全部环路和接入全部DG的情况下，系统的节点电压全都提升到了0.98（pu）之上。

从图3和图4可看出，方式6和方式7中各类型DG输出的三相有功功率不对称，因此，相对于传统算法中近似认为DG三相功率对称的处理方法，本文算法中的处理方法更合理、有效，而且还反映出了三相对称DG接入三相不平衡的主动配电网中会出现DG三相不对称的运行状况。

3.2 算例2

为了进一步验证本文算法的计算性能，参见文献[25]介绍的IEEE 37和IEEE 123母线三相不平衡配电网，以及文献[26]介绍的69母线系统扩展成三相不平衡配电系统，假设算例1中的四种不同类型DG为一组DG集，则在IEEE 37母线系统、69母线系统和IEEE 123母线系统中分别接入1、2和3 组DG集，并且分别增加5、5和8条环路，其中各类型DG并网参数同算例1，但均不考虑无功界限，图5给出了69母线三相不平衡主动配电网单线图。算法程序均基于Matlab语言编写，并且在Windows XP操作系统、Inter CPU 1.6GHz和2GB RAM环境下进行测试，其中收敛精度均为10-6。

下面按照表6中的四种方案进行仿真测试，四种方案下的测试结果分别见表7～表10。

图5　69母线三相不平衡主动配电网Fig.5 69-bus three-phase unbalanced active distribution network

表6　算例2的四种测试方案Tab.6 Four cases of test 2

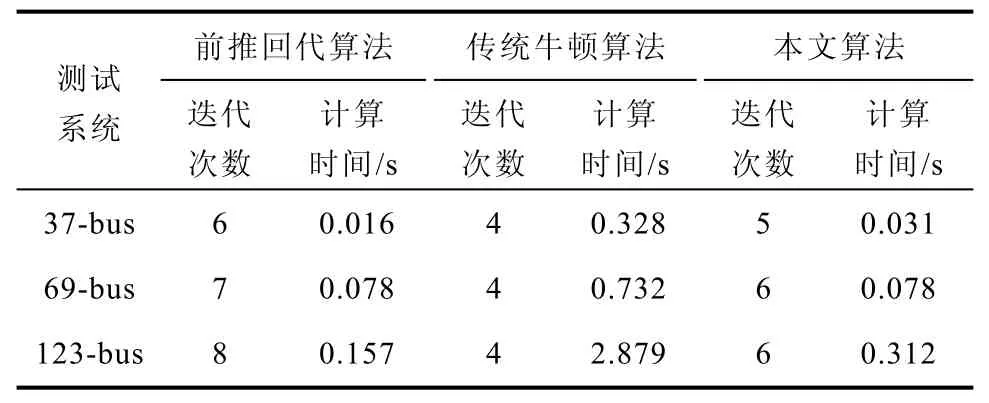
表7　方案1时三种潮流算法的性能比较Tab.7 Performance contrast of three algorithms in case 1

表8　方案2时三种潮流算法的性能比较Tab.8 Performance contrast of three algorithms in case 2

表9　方案3时三种潮流算法的性能比较Tab.9 Performance contrast of three algorithms in case 3

表10　方案4时三种潮流算法的性能比较Tab.10 Performance contrast of three algorithms in case 4

由表7可知，前推回代算法为数值运算，在辐射型配电网中具有最快的计算速度，以及良好的收敛性。传统牛顿算法具有二阶收敛，收敛性最好，但对于三相不平衡的配电系统，每个节点都有6个变量和6个方程，计算出的雅可比矩阵维数较大，所以计算速度慢、时间长以及效率最低。本文算法采用了三序解耦和道路-回路分析法，三序解耦后可以并行计算，所以具有较高的计算速度和效率，以及很好的收敛性。

比较表7和表8可看出，本文算法和传统牛顿算法都具有较强的DG处理能力，因此，DG接入对本文算法和传统牛顿算法基本无影响。但是，由于前推回代算法处理PV节点困难，所以造成了其迭代次数剧增，计算时间较长。

比较表7和表9可看出，本文算法和传统牛顿算法都具有很强的环网处理能力，因此，闭合环路对本文算法和传统牛顿算法影响较小，由于环路闭合缩短了系统的电气距离，从而减少了本文算法的迭代次数。但是，由于前推回代算法处理环网能力较弱，导致其迭代次数剧增，计算时间也较长。

从表10可看出，当闭合环路同时接入DG时，前推回代算法的迭代次数增加更多或根本不收敛，而本文算法和传统牛顿算法的变化都很小。

总体上来看，本文算法和传统牛顿算法都具有较强的DG和环网处理能力，远强于前推回代算法。传统牛顿算法的收敛性要稍优于本文算法，但是，其计算速度和效率要远低于本文算法。综合来讲，在主动配电网三相潮流计算中，本文算法要优于前推回代算法和传统牛顿算法。

4 结论

本文提出了一种能高效处理多类型DG规模化接入和环网的主动配电网三相解耦潮流算法。该算法计算过程清晰，编程简单，容易实现，采用三序解耦及并行计算，极大地提高了算法的计算速度和效率，节省了内存空间，保留了面向支路的前推回代法计算速度快、收敛性稳定的优点。算法中对PQ、PQ（V）、PV和PI节点类型DG规模化并网和无功补偿设备接入的潮流计算模型进行了详细的公式推导，且容易编程实现，另外，通过算法比较测试显示本文算法的计算性能要远优于传统算法。

通过IEEE 37、69和123母线测试系统显示，采用所提算法对主动配电网进行三相潮流计算具有良好的收敛性、很强的多类型DG规模化接入和环网处理能力。另外，从计算结果可看出，DG并网及其输出有功功率和无功功率，可以减少系统线路上功率流动，而闭合环路可以改变主动配电系统的功率流向，缩小系统的电气距离，因此，DG并网和闭合环路都能改善系统各节点电压水平，并且环路闭合时潮流计算收敛更快。另外，当接入以异步发电机的风机作为接口的PQ（V）型DG时，虽然该类型DG从系统中吸收无功功率，但均会安装无功补偿设备对其进行无功补偿，且尽量保证该风力发电机不从系统吸收无功功率。所以，与其他类型DG一样，都具有改善系统电压水平的作用。总的来说，随着增加DG接入和环路闭合的数量，电压水平会得到更好的改善。当然电压改善效果与DG安装的位置、有功和无功输出的多少以及环路的配置密切相关。

参考文献

[1]陈哲.配电系统中的风力发电[J].电工技术学报,2013,28（5）:1-14.Chen Zhe.Wind power in electrical distribution systems[J].Transactions of China Electrotechnical Society,2013,28（5）:1-14.

[2]张丽,徐玉琴,王增平,等.包含分布式电源的配电网无功优化[J].电工技术学报,2011,26（3）:168-174.Zhang Li,Xu Yuqin,Wang Zengping,et al.Reactive power optimization for distribution system with distributed generators[J].Transactions of China Electrotechnical Society,2011,26（3）:168-174.

[3]Puttgen H B,Macgregor P R,Lambert F C.Distributed generation:semantic hype or the dawn of a new era？[J].IEEE Power and Energy Magazine,2003,1（1）:22-29.

[4]王志群,朱守真,周双喜,等.分布式发电对配电网电压分布的影响[J].电力系统自动化,2004,28（16）:56-60.Wang Zhiqun,Zhu Shouzhen,Zhou Shuangxi,et al.Impacts of distributed generation on distribution system voltage profile[J].Automation of Electric Power Systems,2004,28（16）:56-60.

[5]Wang Caisheng,Nehrir M H.Analytical approaches for optimal placement of distributed generation sources in power systems[J].IEEE Transactions on Power Systems,2004,19（4）:2068-2076.

[6]Palma-behnke R,Cerda J L A,Vargas L S,et al.A distribution company energy acquisition market model with integration of distributed generation and load curtailment options[J].IEEE Transactions on Power Systems,2005,20（4）:1718-1727.

[7]王振树,林梅军,刘岩,等.考虑光伏并网的配电网潮流计算[J].电工技术学报,2013,28（9）:178-185.Wang Zhenshu,Lin Meijun,Liu Yan,et al.Power flow algorithm for distribution network with photovoltaic system[J].Transactions of China Electrotechnical Society,2013,28（9）:178-185.

[8]张立梅,唐巍.计及分布式电源的配电网前推回代潮流计算[J].电工技术学报,2010,25（8）:123-130.Zhang Limei,Tang Wei.Back/forward sweep power flow calculation method of distribution networks with DGs[J].Transactions of China Electrotechnical Society,2010,25（8）:123-130.

[9]陈海炎,陈金福,段献忠.含分布式电源的配电网潮流计算[J].电力系统自动化,2006,30（1）:35-40.Chen Haiyan,Chen Jinfu,Duan Xianzhong.Study on power flow calculation of distribution system with DGs[J].Automation of Electric Power Systems,2006,30（1）:35-40.

[10]唐小波,徐青山,唐国庆.含分布式电源的配网潮流算法[J].电力自动化设备,2010,30（5）:34-37.Tang Xiaobo,Xu Qingshan,Tang Guoqing.Power flow algorithm for distribution network with distributed generation[J].Electric Power Automation Equipment,2010,30（5）:34-37.

[11]杨旭英,段建东,杨文宇,等.含分布式发电的配电网潮流计算[J].电网技术,2009,33（18）:139-143.Yang Xuying,Duan Jiandong,Yang Wenyu,et al.Power flow calculation based on power losses sensitivity for distribution system with distributed generation[J].Power System Technology,2009,33（18）:139-143.

[12]朱星阳,张建华,刘文霞,等.考虑负荷电压静特性的含分布式电源的配电网潮流计算[J].电网技术,2012,36（2）:218-223.Zhu Xingyang,Zhang Jianhua,Liu Wenxia,et al.Power flow calculation of distribution system with distributed generation considering static load characteristics[J].Power System Technology,2012,36（2）:218-223.

[13]王建勋,吕群芳,刘会金,等.含分布式电源的配电网潮流快速直接算法[J].电力自动化设备,2011,31（2）:17-21.Wang Jianxun,Lü Qunfang,Liu Huijin,et al.Fast and direct power flow algorithm for distribution network with distributed generation[J].Electric Power Automation Equipment,2011,31（2）:17-21.

[14]王守相,黄丽娟,王成山,等.分布式发电系统的不平衡三相潮流计算[J].电力自动化设备,2007,27（8）:11-15.Wang Shouxiang,Huang Lijuan,Wang Chengshan,et al.Unbalanced three-phase flow calculation for distributed power generation system[J].Electric Power Automation Equipment,2007,27（8）:11-15.

[15]Zhu Y,Tomsovic K.Adaptive power flow method for distribution systems with dispersed generation[J].IEEE Transactions on Power Delivery,2002,17（7）:822-827.

[16]Tong S,Miu K.A network-based distributed slack bus model for DGs in unbalanced power flow studies[J].IEEE Transactions on Power Systems,2005,20（2）:835-842.

[17]赵晶晶,李新,许中.含分布式电源的三相不平衡配电网潮流计算[J],电网技术,2009,33（3）:94-98.Zhao Jingjing,Li Xin,Xu Zhong.Calculation of three-phase unbalanced power flow in distribution network containing distributed generation[J].Power System Technology,2009,33（3）:94-98.

[18]李红伟,张安安.含PV型分布式电源的弱环配电网三相潮流计算[J].中国电机工程学报,2012,32（4）:128-135.Li Hongwei,Zhang An’an.Three-phase power flow solution for weakly meshed distribution system including PV type distributed generation[J].Proceedings of the CSEE,2012,32（4）:128-135.

[19]丁明,郭学凤.含多种分布式电源的弱环配电网三相潮流计算[J].中国电机工程学报,2009,29（13）:35-40.Ding Ming,Guo Xuefeng.Three-phase power flow for the weakly meshed distribution network with the distributed generation[J].Proceedings of the CSEE,2009,29（13）:35-40.

[20]黄少伟,陈颖,沈沉.不对称电力系统相序混合建模与三相潮流算法[J].电力系统自动化,2011,35（14）:68-73.Huang Shaowei,Chen Ying,Shen Chen.Hybrid modeling of asymmetrical power system and threephase power flow method[J].Automation of Electric Power Systems,2011,35（14）:68-73.

[21]Abdel-akher M,Nor K M,Rashid A H A.Improved three-phase power-flow methods using sequence components[J].IEEE Transactions on Power Systems,2005,20（3）:1389-1397.

[22]张小平,陈珩.不对称三相潮流的对称分量分析法[J].中国电机工程学报,1993,13（6）:1-12.Zhang Xiaoping,Chen Heng.Unsymmetrical three-phase load flow study based on symmetrical component theory[J].Proceedings of the CSEE,1993,13（6）:1-12.

[23]张伯明,陈寿孙,严正.高等电力网络分析[M].北京:清华大学出版社,2007.

[24]王成山,孙充勃,彭克,等.微电网交直流混合潮流算法研究[J].中国电机工程学报,2013,33（4）:8-15.Wang Chengshan,Sun Chongbo,Peng Ke,et al.Study on AC-DC hybrid power flow algorithm for microgrid[J].Proceedings of the CSEE,2013,33（4）:8-15.

[25]Kersting W H.Radial distribution test feeders[J].IEEE Transactions on Power Systems,1991,6（3）:975-985.

[26]王守相,王成山.现代配电系统分析[M].北京:高等教育出版社,2007.

杨 雄 男，1983年生，博士，工程师，研究方向为新能源技术及配电系统自动化。

E-mail:hhyangxiong@126.com（通信作者）

卫志农 男，1962年生，博士，教授，博士生导师，研究方向为电力系统运行、分析与控制和输配电系统自动化。

E-mail:znwei@hhu.edu.cn

Three-Phase Decoupled Power Flow Algorithm for Active Distribution Networks

Yang Xiong1,2Wei Zhinong1Sun Guoqiang1Sun Yonghui1Yang Yongbiao3Chen Lu3
（1.Hohai University Nanjing 210098 China 2.Jiangsu Electric Power Company Research Institute Nanjing 211103 China 3.NARI Technology Development Limited Company Nanjing 211106 China）

AbstractWith the development of active distribution network technologies and the connection of large-scale distributed generations（DGs）to active distribution networks,the traditional power flow methods are difficult to meet power flow calculation for active distribution networks.Therefore,in this paper,a three-phase decoupled power flow algorithm for active distribution networks is proposed,which has high efficiency of processing multi-type large-scale DGs and meshed networks.The proposed algorithm uses the sequence component analysis approach and the three-sequence decouplingcompensation models of unsymmetrical branches,and combines the special topological structure of active distribution network with the path-loop analysis approach.The power flow models of the large-scale PQ-node,PQ（V）-node,PV-node and PI-node type DGs and the var compensators are derived in detail,and the three-phase decoupled power flow can be parallel calculated with smaller CPU time and less memory space.The results of IEEE 37-bus,69-bus and 123-bus test systems verify the effectiveness and good convergence of the proposed algorithm.Meanwhile,it is shown that the proposed algorithm has strong ability to process multi-type large-scale DGs and meshed networks,and is superior to the traditional algorithms.

Keywords：Active distribution network,three-phase decoupled,power flow calculation,meshed network,distributed generation,three-phase unbalanced,reactive compensation

作者简介

收稿日期2014-01-03 改稿日期 2014-02-19

中图分类号：TM743