一种港口塔吊水平风荷载预报模型的设计和实现*
2016-05-05项青霞蒋琳琳
龙 强,王 畅,王 锋,2,项青霞,蒋琳琳
(1.曹妃甸工业区气象局,河北 唐山 063015;2.唐山市气象局,河北 唐山 063000;
3.冀东油田志达公司,河北 唐山 063020)
一种港口塔吊水平风荷载预报模型的设计和实现*
龙强1,王畅1,王锋1,2,项青霞1,蒋琳琳3
(1.曹妃甸工业区气象局,河北 唐山 063015;2.唐山市气象局,河北 唐山 063000;
3.冀东油田志达公司,河北 唐山 063020)
摘要:利用2012-06—2013-05渤海湾北岸曹妃甸港100 m风能塔风观测资料,研究了空气动力学粗糙度z0的月变化特征及其和地面10 m风速之间的关系,并针对港口安全运营调度精细化气象服务保障需求,设计了一种港口塔吊定点、定量水平风荷载的预报模型。结果表明:受海陆风和周围环境的季节性变化影响,渤海湾北岸z0具有明显的月变化特征;通过拟合确立了z0和地面10 m处10 min平均风速在海-陆风和陆-海风两个方位上的粗糙度方程,梯度风速计算试验显示方程稳定可用;基于以上结论建立了定点、定量风荷载预报模型,预报试验和程序开发结果表明,基于上述结论所建立的港口塔吊水平风荷载计算模型正确可行,更适用于风险预报业务。
关键词:空气动力学粗糙度;梯度风;风荷载;预报模型
除了地震作用的水平力外,高层构筑物主要的侧向荷载是风荷载,在荷载组合时往往起控制作用。风荷载是结构设计的控制因素之一,高层构筑物在水平风荷载作用下的结构分析和设计引起了研究人员和工程师越来越多的重视[1-2]。对于垂直于建(构)筑物表面上的风荷载标准值的计算,GB 50009—2001 《建筑结构荷载规范》有相关说明和规定[3]。目前对风荷载的相关技术规定和科学研究大多停留在设计阶段,仅作工程项目风险评估使用[4-7]。然而,工程项目落地并投入使用后,构筑物在日常的运营作业中所面临的情况要复杂一些[8-9],不同地区和下垫面条件下的相关指标和参数不一,将参数统一或归类所获得的风荷载阈值并不能满足安全管理人员对了解构筑物承受实时风荷载情况的需求,也无法实现对未来风向、风速条件下构筑物所承受风荷载的风险预报。因此,设计一种便捷可用的构筑物实时水平风荷载计算模型对作业的安全运营保障具有重要的现实意义。
以塔吊这一港口重要的构筑物作为研究对象,以渤海湾北岸曹妃甸港为设计案例,通过分析计算风能塔观测资料,获取空气动力学粗糙度特征,推算垂直梯度风,并基于伯努利方程,对接气象数值预报产品设计了一种港口塔吊水平风荷载的实时计算和预报预测模型。
1资料与方法
研究所用数据来自建在渤海湾北岸的100 m风能塔,其位于一个三面环海的半岛上,共有5层观测平台,分别为100,70,50,30和10 m。风能塔所在的位置如图1所示。按照方向划分,135°~315°为海-陆风方向(即风由海面吹向陆地),0°~134°和316°~360°为陆-海风向(即风由陆地吹向海面)。
选取了2012-06-2013-05共计12个月(4个季节)的风速、风向等观测数据,数据时间分辨率为1 h。
图1 渤海湾北岸相关观测站点的分布Fig.1 Locations of the related observation stations on the northern coast of the Bohai Bay
1.1空气动力学粗糙度z0
计算空气动力学粗糙度常用的方法有对数廓线拟合法、阻力法、质量守恒法、压力中心法以及无因次化风速法。文中主要采用的是阻力法,其公式为
(1)
式中,σu为常数;U(zn)为高度zn处的风速;κ是卡门常数,一般取0.4;Cu也为常数,和测风仪器有关;zn具有长度量纲。上式适用于强风状况(U(z)>4.0 m/s)。根据数据实际情况和所采用的方法要求,需要对测风塔的观测数据进行质量控制。
采用不同高度处的风速带入上式,做商即可消去相关常数,获得空气动力学粗糙度z0的值。
(2)
式中,zn为上层某一高度,U(zn)即为该高度处的风速。由于气象学地面风观测是位于10 m高度处,数值预报产品也是10 m高度处风速,结合研究应用需求,此次确定z为10 m,U(z)即为10 m高度处的风速。
为进一步分析空气动力学粗糙度随季节、风向和下垫面的变化及不同计算方法的适用情况,在z0特征分析部分增加了对数廓线拟合计算方法。对数廓线拟合法需要测得3个或3个以上高度的风速,用最小二乘回归所得的风速资料为
U(zn)=a+blnzn。
(3)
按照粗糙度的定义,令式(3)中U(zn)=0即可得空气动力学粗糙度z0
(4)
对数廓线拟合法更适用于中性大气层结条件,风速符合对数分布,对所测的风速廓线质量要求较高。
1.2基于z0的港口塔吊水平风荷载计算模型
风压是垂直于气流方向的平面单位面积所受到的风的压力,根据伯努利方程可得出风-压关系。[10]边界层内港口塔吊水平风荷载的实时计算可忽略近地层空气密度的变化影响,标准状态下用风速估计风压的通用公式[11]为
(5)
式中,wp为风压。根据式(3)则可以计算出zn高度处ds面积的风荷载F(zn):
F(zn)=wp·ds=U(zn)2·ds/1 600,
(6)
将塔吊机身视作矩形平面,便有ds=L·dzn,L为塔吊机身的宽。对式(4)采用垂直高度上的积分即可得塔吊水平风荷载Fc:
(7)
式中,H为塔吊的高度,θ为风向和塔吊平面的夹角(锐角)。
由式(1)和(7)可知,实现垂直塔臂水平风荷载Fc的计算,主要是研究分析空气动力学粗糙度z0的特征和计算方法。
2z0的特征分析
2.1z0的月变化特征
原始资料经过质量控制和筛选(U(z)>4.0 m/s)之后,通过式(2)和(3)得到空气动力学粗糙度z0随月份的变化关系。由图2可知:阻力法和对数廓线拟合法的计算结果整体相差不大,随季节的变化趋势相同,但后者的计算值在夏季(6,7和8月)比前者偏小,在冬季(12,1和2月)则明显相反,这是由于冬季层结整体较夏季稳定,对数廓线拟合法更适用于稳定层结条件;海-陆风、陆-海风条件下z0均具有明显的季节性特征,春、夏季(3,4,5月和6,7,8月)的z0值明显偏大,以6月的值最大,秋、冬季节(9,10,11月和12,1,2月)的z0值偏小,以12月的值最小。海-陆风和陆-海风的春季空气动力学粗糙度的平均值分别是1.12 和0.24 m(阻力法计算结果,下同),夏季的平均值分别是0.79和0.22 m,秋季的平均值均为0.09 m,冬季的平均值是0.12和0.11 m,可见海-陆风的空气动力学粗糙度整体较陆-海风的偏大,这与风向划分的实际是相符的。空气动力学粗糙度出现这种季节性特征的主要原因是受周围环境的影响,对陆-海风而言,春、夏季的低矮植被相对茂盛,粗糙度较大;海-陆风条件下风从海面吹来,不同季节风速情况相差显著[12],使得空气动力学粗糙度也有季节性差别。
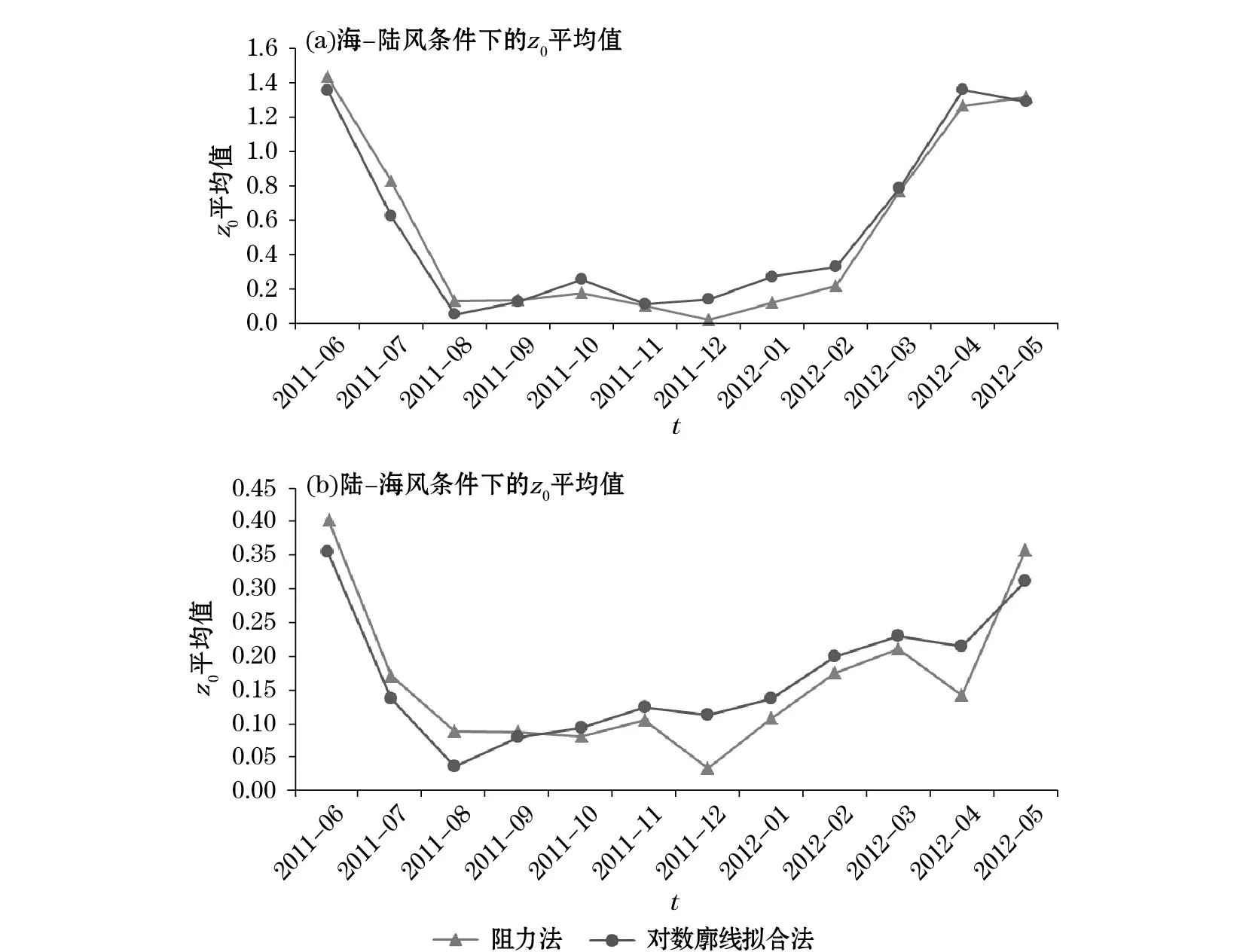
图2 海-陆风和陆-海风条件下空气动力学粗糙度z0随月份的变化Fig.2 The monthly variations of aerodynamic roughness z0 under the sea-land and the land-sea breeze conditions
2.2z0与风速的变化关系
利用式(2)计算得到在海-陆风条件下的空气动力学粗糙度z0的平均值是0.59 m,陆-海风条件下的平均值是0.20 m。为了更加准确地获取不同风速下的粗糙度值,分析了10 m处风速和空气动力学粗糙度的关系,并根据数值分布特征对粗糙度值和地面10 min平均风速做了公式拟合,如图3所示。
由图3可知,z0并不是一固定常数,且与10 m风速的变化也并非是线性关系。这是因为空气动力学粗糙度在偏小的情况下,风速便增加,近地层空气局部流动脉动便增强,风动量能更低地到达地面,使阻力系数减小,流体本身受到的阻力也就减小。所以在确定空气动力学粗糙度时,不能仅仅考虑下垫面的性质,还须考虑风速和流场的性质。同样,z0也不仅仅反映了下垫面的粗糙特性,也是反映下垫面和近地表流场相互作用的物理量。拟合结果显示,无论是海-陆风还是陆-海风,z0与10 m风速之间存在着良好的指数关系。
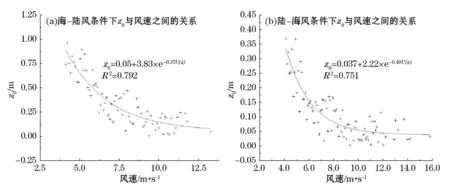
图3 海-陆风和陆-海风条件下z0与风速间的关系Fig.3 Relationship between z0 and wind speed under the sea-land and the land-sea breeze conditions
2.3梯度风的计算及检验
在获取了空气动力学粗糙度z0值之后,即可根据式(2)计算垂直某一层的风速,即
(8)
对于z0值的确定,大多采用多样本计算取平均值,忽略不同风速条件下的不同。但我们认为直接采用空气动力学粗糙度平均值计算梯度风速和采用z0拟合公式所计算的梯度风速在准确率上应该有所区别。海-陆风条件下1 946个个例、陆-海风条件下2 009个个例的计算结果表明:整体而言,采用粗糙度方程所计算的梯度风速更接近于实况,平均误差明显偏小。图4是随机挑取的100个个例检验结果,由图可见,通过粗糙度公式所计算的梯度风速优于采用z0平均值计算的结果。因此,文中所得的粗糙度和风速之间的关系能够较好地体现本地空气动力学粗糙度特征,更适用于计算本地的梯度风速。
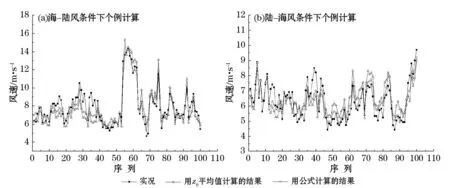
图4 海-陆风和陆-海风条件下的个例检验计算Fig.4 Case of test calculation under the sea-land and the land-sea breeze conditions
3基于粗糙度z0的风荷载计算模型
港口塔吊水平风荷载的实时和预报计算模型的基本框架如图5所示,通过10 m高度处的风观测实况值或数值预报产品(NWP)10 min平均风速预报值,利用风向划分为海-陆风或陆-海风,代入指数拟合公式获得z0值;将z0代入式(8)便可求得zn高度处的风速,通过式(7)即可计算出塔吊垂直塔臂的水平风荷载Fc的值。
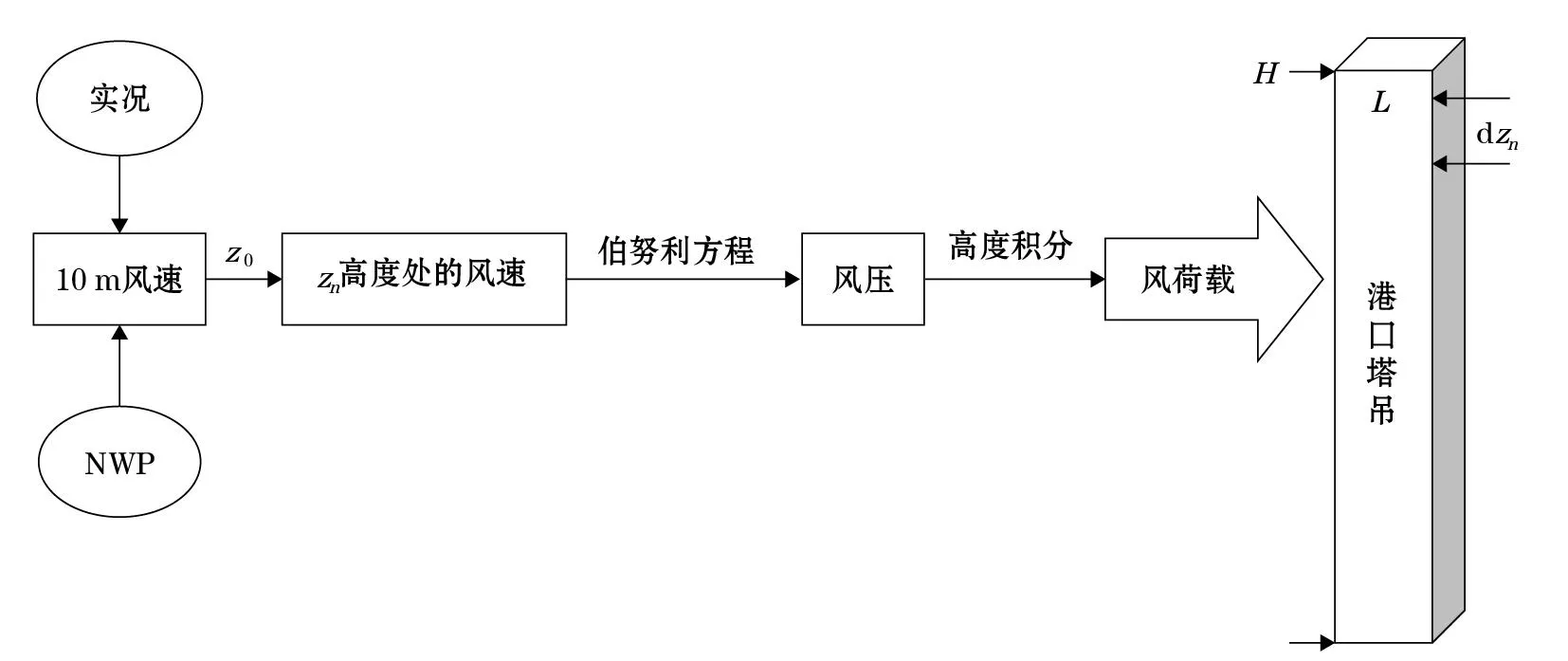
图5 港口塔吊风荷载计算模型框架Fig.5 Framework of wind load computation model for a port crane
综上所述,由式(1)、(7)及海-陆风、陆-海风的z0拟合公式便可得水平风荷载Fc。
海-陆风条件下的水平风荷载:
(9)
陆-海风条件下的水平风荷载:
(10)
也可通过式(7)、(8)及海-陆风、陆-海风的z0拟合公式得到消减相关参数的Fc。
海-陆风条件下的水平风荷载:
(11)
陆-海风条件下的水平风荷载:
(12)
由式(11)、(12)可以看到,水平风荷载Fc的计算最终变为关于zn较为简单的积分,即:
(13)
基于地面10 m风速实况或风速预报值,分别代入海-陆风和陆-海风条件下的粗糙度z0求积分值,即可计算塔吊的水平风荷载。
在预报业务应用方面,对接数值预报产品,自动输出塔吊水平风荷载预报值,参照项目设计阶段所确定的风荷载阈值,实现不同风条件下的塔吊风险评估,提前做好作业安排。平台开发设计框架如图6所示。
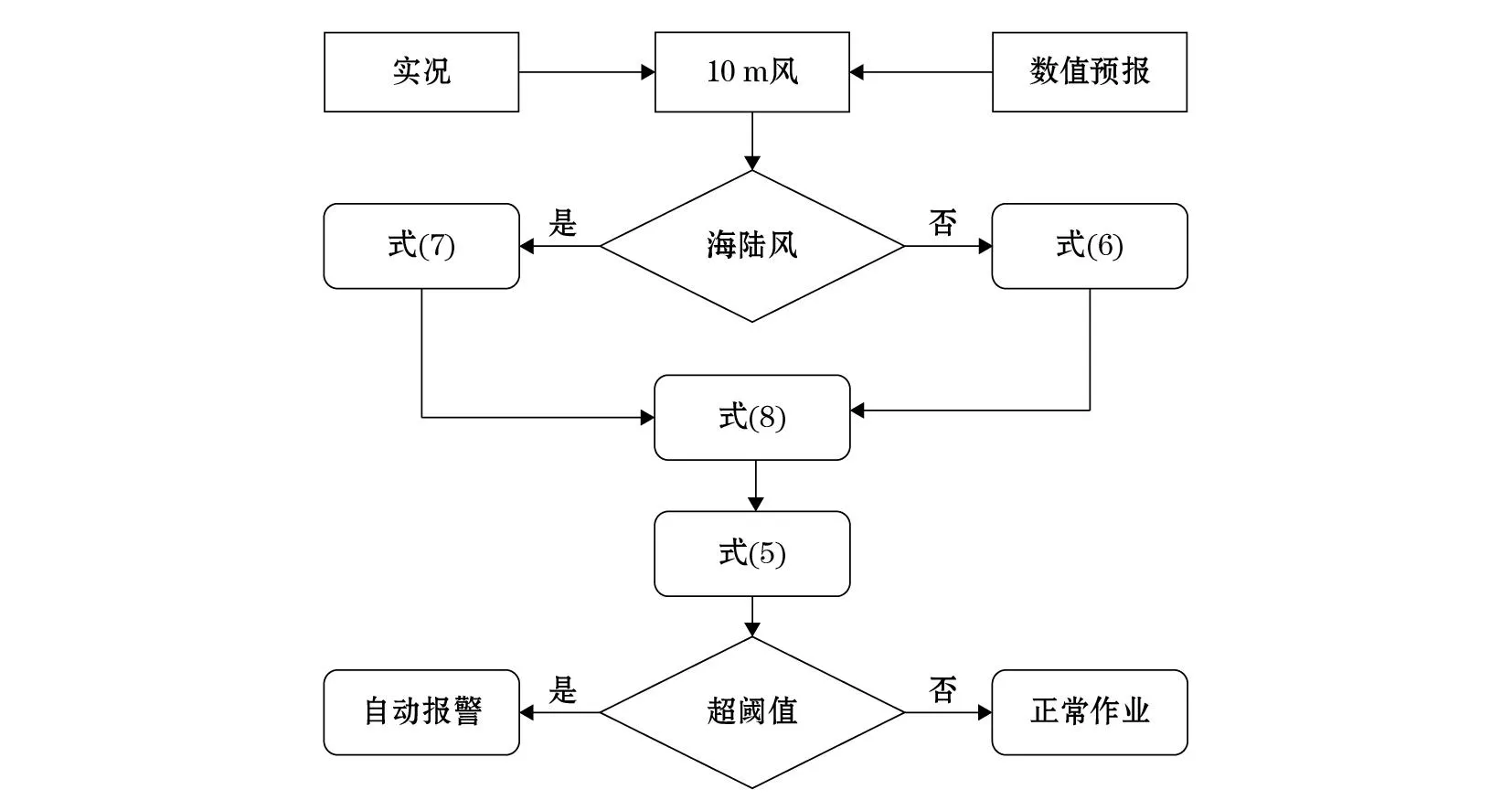
图6 程序设计框架图Fig.6 Framework of the program design
为了评估模型的适用性,选取了2015-08的风速实况进行试验(预报效果取决于风速的预报,原理同实况检验)。表1为渤海湾北岸曹妃甸港口南北方向上塔吊(偏东方向作业,垂直单臂起重机)的水平风荷载指标,风等级以平均风速划分。由表可知,通过该模型所得的风险警报指标(停止作业指标在警报指标上增加1级)和安全运营调度所设计的阈值基本一致,整体略偏小,这是由于在考虑塔吊截面时,忽略了塔机高度,将垂直单臂视作立方体所致。
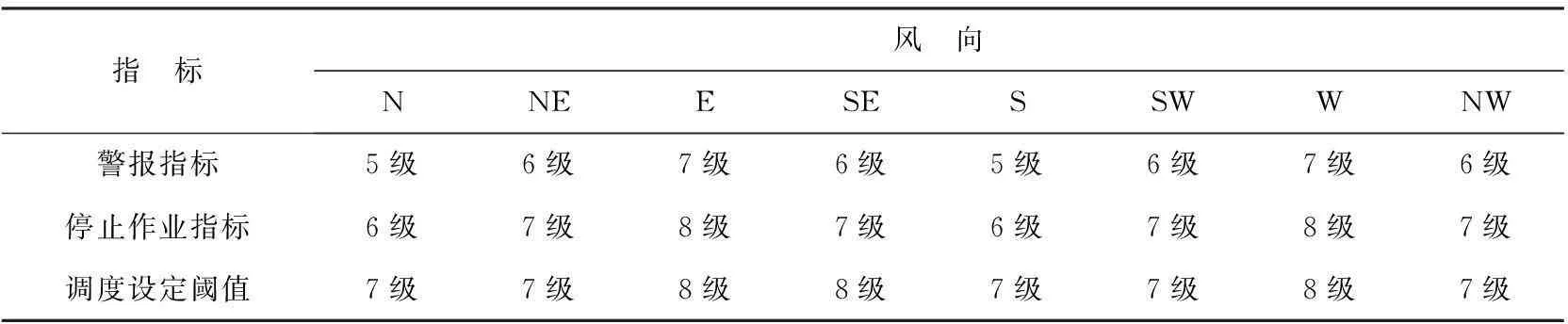
表1 曹妃甸港口塔吊安全运营调度风等级指标
对于龙门吊、十字起重机等其他形式的塔吊,同样适用于该方法,垂直方向的风荷载仍然采用上述方法,水平方向上由于不存在梯度风差异(水平塔臂的垂直高度较小,忽略垂直方向上风速的不同),可计算该高度处的梯度风速,求得水平塔臂的风荷载:
(14)
式中,h为水平塔臂所在的高度,U(h)可通过式(8)求得,Ss为水平塔臂的平面面积,为固定值。因此,十字起重机的风荷载F=υ·(Fc+Fs),υ为因镂空所致的削减系数,为0~1;而龙门吊由于有2条垂直塔臂,整体的水平风荷载F=2Fc+Fs。
4结论
1)受海陆风和周围环境的季节性变化影响,渤海湾北岸z0具有明显的月变化特征,突出表现在春、夏季(3,4,5月和6,7,8月)的z0值明显偏大,以6月的值最大,秋、冬季节(9,10,11月和12,1,2月)的z0值偏小,以12月的值最小。
2)通过拟合确立了z0和地面10 m处10 min平均风速在海-陆风和陆-海风两个方位上的粗糙度方程,二者之间存在较为稳定的指数关系,梯度风速计算试验显示方程稳定可用,采用方程计算比用平均值计算的梯度风速效果更理想。
3)基于空气动力学粗糙度所设计的风荷载计算模型实现了对实况值的把握和对未来不同风条件下构筑物的风险评估,该模型简单可用,可实现定点、定量值的预报,且便于程序开发和实现,个例计算试验表明该模型可以应用于构筑物安全运营调度的保障业务中,且适用于龙门吊、十字起重机等多种类型的塔吊。
参考文献:
[1]周红波, 黄誉. 超高层建筑在极端台风气候下结构及施工安全风险分析及控制研究[J].土木工程学报, 2014, 47(7): 126-135.
[2]吴甬春, 张皖华, 叶小刚, 等. 塔吊倾覆力矩的计算[J].科技信息, 2007, (24): 352,374.
[3]建筑结构荷载规范:GB 50009-2001[S].北京:中国建筑工业出版社,2006.
[4]郑永胜, 李雪梅, 王莹. 风荷载在地质灾害中的作用[J].世界地质, 2007,26(3): 333-337.
[5]孙作玉, 王晖. 高耸结构随机风荷载的数值模拟[J].广州大学学报(自然科学版), 2008, 7(5): 79-83.
[6]徐永林, 朱元清, 周晶矛, 等. 超高层建筑风荷载计算中的振型函数[J].地震地磁观测与研究, 2010,31(3): 111-114.
[7]张苏俊, 谢瑞峰. 风荷载下轻质木框架房屋结构的有限元分析[J].扬州大学学报(自然科学版), 2013,16(4): 70-73,82.
[8]陈晖, 曹立华, 李安龙, 等. 埕岛海域浅水区人工构筑物周边海底地形演化与海洋灾害地质现象关系研究[J].海岸工程, 2003, 22(3): 19-24.
[9]褚宏宪, 原晓军, 张晓波, 等. 石岛新港港池回淤变化分析[J].海岸工程, 2009, 28(4): 1878-1881.
[10]苏志, 张瑞波, 周绍毅, 等. 北部湾沿海基本风压和阵风风压分析[J].热带地理, 2010, 24(2): 141-144.
[11]袁春红,薛桁,杨振斌.建筑风荷载风压计算中的若干问题[J].气象,2002,28(1):39-41.
[12]龙强, 孟艳静, 王锋, 等. 唐山曹妃甸海域风特征的初步分析[J].河北气象, 2013, 32(1): 14-17.
Design and Implementation of Horizontal Wind Load Forecasting Model for Port Cranes
LONG Qiang1,WANG Chang1,WANG Feng1,2,XIANG Qing-xia1,JIANG Lin-lin3
(1.CaofeidianIndustrialDistrictMeteorologicalBureau, Tangshan 063015, China;
2.TangshanMeteorologicalBureau, Tangshan 063000, China;3.PetroChinaJidongOilfieldZhidaCompany, Tangshan 063200, China)
Abstract:The monthly changing characteristics of aerodynamic roughness z0 and the relationship between z0 and the average wind speed at 10 meters above the ground are investigated by using the wind data observed on a 100-meter-high wind energy tower located at the Caofeidian Port on the northern coast of the Bohai Bay from June 2012 to May 2013. The results have indicated that because of the influences of seasonal changes in land and sea breeze and surrounding environment the z0 on the northern coast of the Bohai Bay varies monthly and significantly. By using fitting methods, equations are built up between the z0 and the 10min average wind speed at 10 meters above the ground in the sea-land and the land-sea breeze directions. The gradient wind speed calculation tests have indicated that the above two equations are stable and practicable. Based on all the above conclusions, a fixed point and quantitative horizontal wind load forecasting model for port cranes is designed and established for the requirements of fine weather service support for safety operation dispatching of the port. The results from the tests of the forecasting model and the program developments have shown that the forecasting model thus established is correct, feasible and even more suitable for the risk forecasting service.
Key words:aerodynamic roughness; gradient wind; wind load; forecasting model
中图分类号:P732
文献标识码:A
doi:10.3969/j.issn.1002-3682.2016.01.007
作者简介:龙强(1987-),男,工程师,硕士,主要从事海洋预报方面研究.E-mail:q_loong@126.com(王燕编辑)
收稿日期:2015-09-30
文章编号:1002-3682(2016)01-0066-09
资助项目:中国气象局气象关键技术集成与应用项目——黄渤海港口安全运营气象服务技术集成与示范(CMAGJ2015M5)
