基于两点交叉多子代遗传算法
2016-05-05王福林付晓明朱会霞赵胜雪东北农业大学工程学院哈尔滨50030辽宁工业大学管理学院辽宁锦州00
王福林,付晓明,朱会霞,赵胜雪(.东北农业大学工程学院,哈尔滨 50030;.辽宁工业大学管理学院,辽宁 锦州 00)
基于两点交叉多子代遗传算法
王福林1,付晓明1,朱会霞2,赵胜雪1
(1.东北农业大学工程学院,哈尔滨150030;2.辽宁工业大学管理学院,辽宁锦州121001)
摘要:针对目前遗传算法局部搜索能力差、收敛精度低问题,提出基于两点交叉多子代遗传算法(TPCMCGA),阐明该算法优越性,并给出多子代个体产生方法。该方法可增加优秀个体概率及算法在当前最优解周围搜索精度,提高算法局部搜索能力。在进化策略中引入种群内部竞争操作,使种群在有限生存空间内加速进化,提高算法运算速度。结果表明,与传统遗传算法相比,TPC-MCGA平均计算时间减少31%~36%,平均迭代次数减少50.2%~51.6%,TPC-MCGA运算速度与最优解精度均明显提高。
关键词:多子代遗传算法;两点交叉;子代数量;进化策略
王福林,付晓明,朱会霞,等.基于两点交叉多子代遗传算法[J].东北农业大学学报,2016,47(3):72-79.
Wang Fulin,Fu Xiaoming,Zhu Huixia,et al.Multi-child genetic algorithm based on two-point crossover[J].Journal of Northeast Agricultural University,2016,47(3):72-79.(in Chinese with English abstract)
遗传算法(Genetic algorithm,GA)是借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应智能优化算法[1-3],由John H.Holland教授于1975年首次提出[4]。与传统优化算法相比,遗传算法具有良好鲁棒性、灵活性、通用性及较强全局搜索能力[5-7],受到广泛关注。但遗传算法局部搜索能力较差,算法进化后期搜索效率较低、收敛精度和运算速度均难提高[8-9]。针对遗传算法不足,近年研究者不断改进。Zhang等在遗传算法中引入模拟退火机制,将模拟退火与遗传算法结合,提高算法局部搜索能力[10]。Chen和Wang等为提高遗传算法寻优性能,将个体通过碱基编码成生物分子,借鉴生物分子操作提高遗传算法搜索效率和寻优性能[11-12]。徐梅等提出一种改进遗传算法初始种群产生方法,提高遗传算法求解有约束问题搜索能力[13]。Saitoh等设计一种新量子遗传算法,在每代所有染色体上根据量子交叉法交叉,实现二次加速,提高遗传算法搜索能力[14]。王福林等提出一种改进进化策略遗传算法,避免变异过程对交叉产生优秀个体破坏,提高遗传算法运算速度[15]。本研究以生物学原理为基础,针对目前遗传算法局部搜索能力差,运算速度慢、收敛精度低问题,将生物学中“多子代”思想和“种群内部竞争”机制引入遗传算法中,提出基于两点交叉多子代遗传算法(Two-point crossover multichild genetic algorithm,TPC-MCGA)。旨在解决目前遗传算法局部搜索能力差、运算效率低问题,为充分发挥遗传算法性能、提高算法求解能力提供有效途径,为多子代遗传算法应用提供理论基础。
1 遗传算法基本假设
遗传算法中存在如下基本假设①存在由多个生物个体组成种群;②生物个体之间存在差异,或群体具有多样性;③生物能够自我繁殖;④不同个体具有不同环境生存能力,具有良好基因结构个体繁殖能力强,反之则弱[16]。在遗传算法实际应用中,假定种群规模始终保持不变,实际是隐含种群容量已饱和、种群容量受限假设。
2 多子代遗传算法概念及其分析
多子代遗传算法对多子代遗传算法定义如下:
父代个体交叉产生子代个体数量多于其父代个体数量遗传算法,称为多子代遗传算法(Multichild genetic algorithm,MCGA)。
在多子代遗传算法中,子代个体数量一般是父代个体数量整数倍。令父代个体数量为N0,子代个体数量为N1时,有
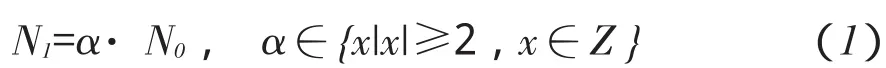
其中,α-子代个体数量与其父代个体数量比例系数。
由式(1)可知,MCGA子代数量较多,在有限生存空间条件下,种群个体生存压力增大,种群个体相互竞争。在竞争过程中,依据优胜劣汰原则[18],竞争获胜优秀个体生存,竞争失败个体淘汰。因此,与传统GA相比,MCGA种群个体间竞争加剧,优胜劣汰速度和种群进化速度加快。
3 多子代遗传算法理论基础
3.1生物学基础
达尔文进化论中生物进化论自然选择学说[17]包括高度生育率、生存斗争、不定变异、最适者生存和受惠种族等因素。生物界中一对父代个体繁殖子代个体数量多于两个,物种在进化过程中不但能继承父代个体特征,有利于在复杂变化自然环境中生存,生物物种不断进化,得到更优良个体。而由父代个体产生子代个体数量小于或等于父代个体数量种群并不存在,即便存在,产生后代个体数量较少,导致有利生存基因在进化中受外界环境因素影响而消失。
动植物父代产生子代数量大多大于父代数量,多子代遗传算法正是基于生物学原理而提出。
3.2数学生态学基础
对种群规模增长和下降研究,是数学生态学最古老分支[18-19]。为说明一个种群能够持续生存条件,需先讨论种群灭绝概率,假设一个种群开始只有一个个体,在某一时间t其规模将为0概率是
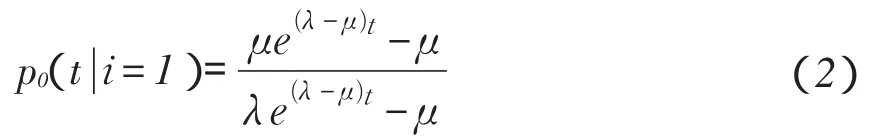
式中,i-初始种群数量,μ-死亡率,λ-生殖率。
关于式(2)推导过程请详见文献[18],如果初始大小为i种群变到灭种,可见i个独立家系均不存在,即对于任意i,这种事件概率是
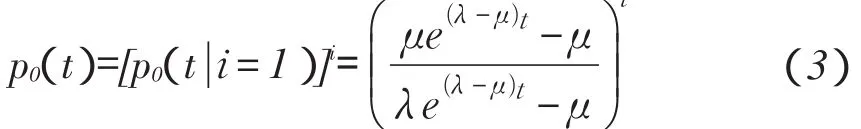
要求出种群最终灭种概率,须使t趋于无穷。故对式(3)分三种情况讨论:
a.当生殖率小于死亡率时,即λ<μ时
显然,在式(3)中指数项随t→∞而变为0,因
此可得:

概率为1,显然该种群无法延续。
b.当生殖率大于死亡率时,即λ>μ时
则当t→∞时,式(3)可化为
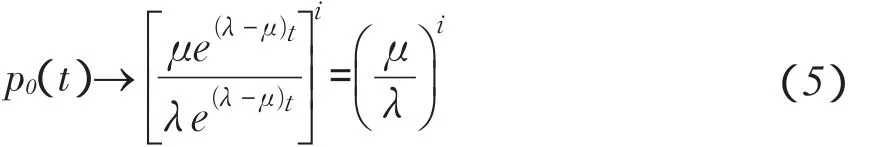
仍有可能灭种,但生殖率超过死亡率越多,生物灭种概率越小。
c.当生殖率等于死亡率时,即λ=μ时
将式(3)中指数项展开成级数形式,并令λ-μ= r,来求tl→im∞p(0t),因此
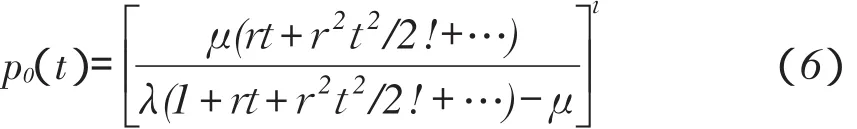
当r→0时,r2项忽略,并且因为λ-μ=r,μ→λ,所以
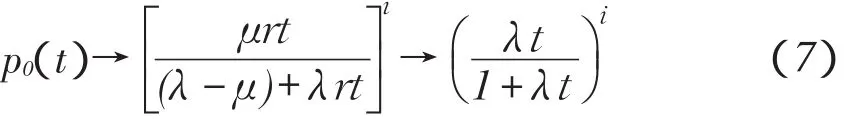
显然,

由此可见,即使生殖率等于死亡率,也会最终灭种。仅当λ>μ时,即种群有正增加率,种群才有可能(并非必然)保持。数学生态学证明了当生物初始种群数量已知时,生物种群规模取值概率分布只取决于每个个体增加率与时间乘积,所以高生殖率保持较短时间,和低生殖率保持较长时间,只要每个个体增加率与时间乘积相等,就会得到相同结果,因此为在最短时间内得到更加优良个体,需要提高物种生殖率。
4 TPC- MCGA子代产生方法
传统遗传算法交叉操作是两个父代生成两个子代,而TPC-MCGA是两个父代个体交叉产生两个以上子代个体。假设有被选择参与交叉两个父代个体P1和P2,其编码长度均为l,随机产生n(2< n≤l-1)个交叉点,则P1和P2染色体被分成n+1段,即P1=A1A2A3…Ak…An- 1AnAn + 1,P2=B1B2B3…Bk…Bn-1BnBn+1。TPC-MCGA子代产生方法是:首先在n个交叉点中任意选择2个交叉点,把这两个交叉点间所包括等位基因看作子串,交换两个父代P1和P2子串形成两个子代个体Child1和Child2;再在n个交叉点中任意选择与之前非重复2个交叉点,交换两个父代P1和P2子串形成两个子代个体Child3和Child4;以此类推,两个父代P1和P2可经过Cn2次非重复交叉,最多可产生2Cn2个不同新子代个体。有如下定义:
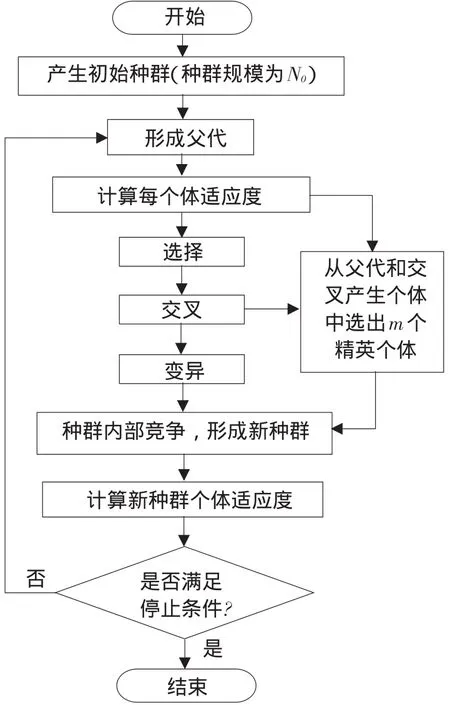
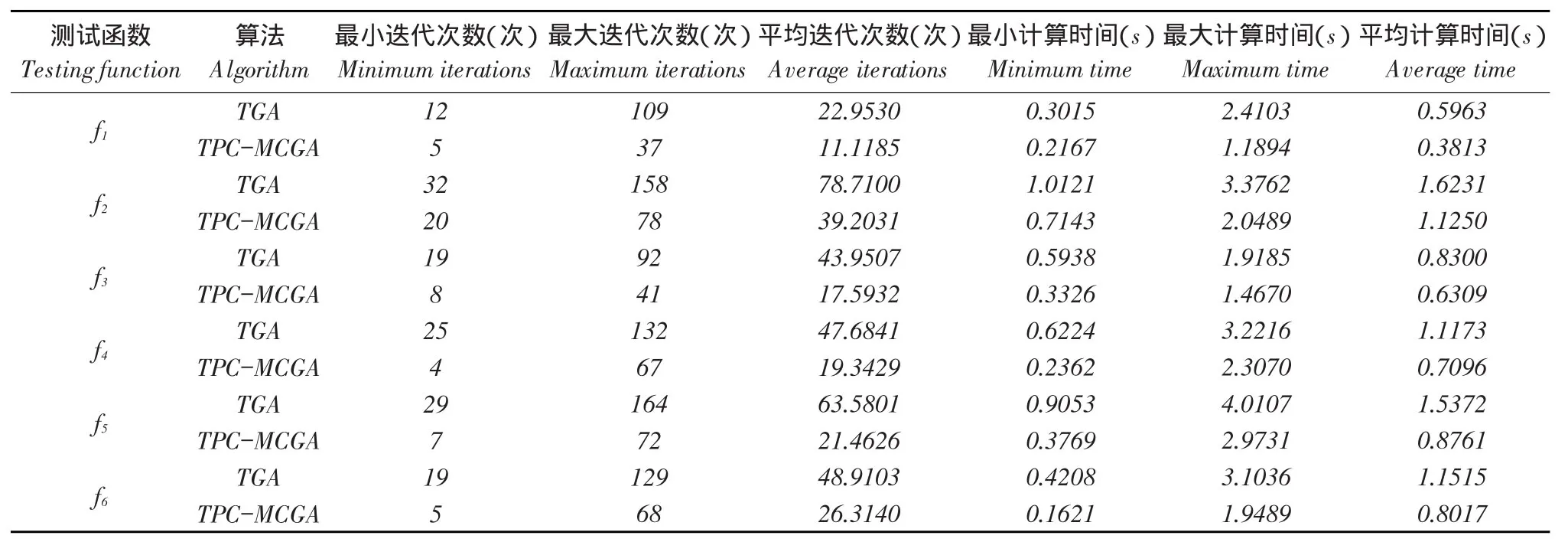
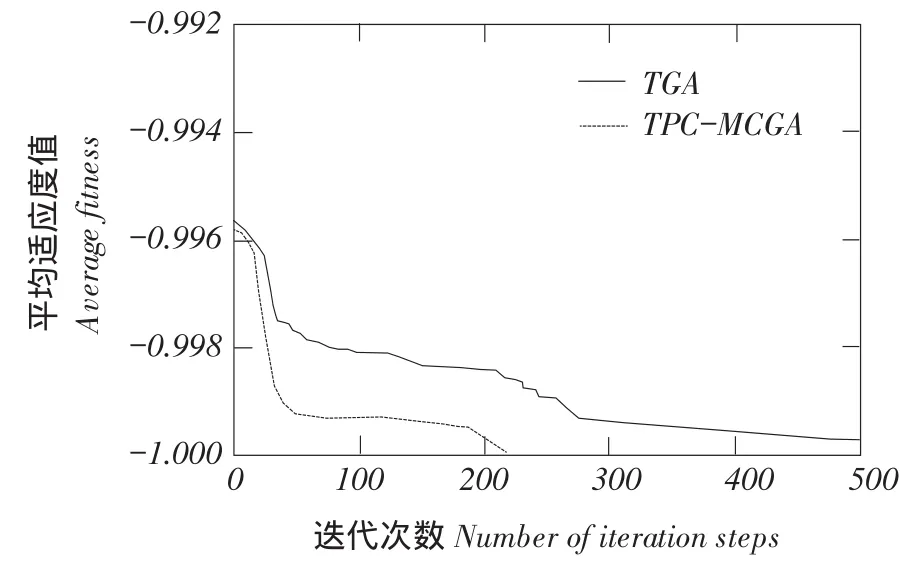
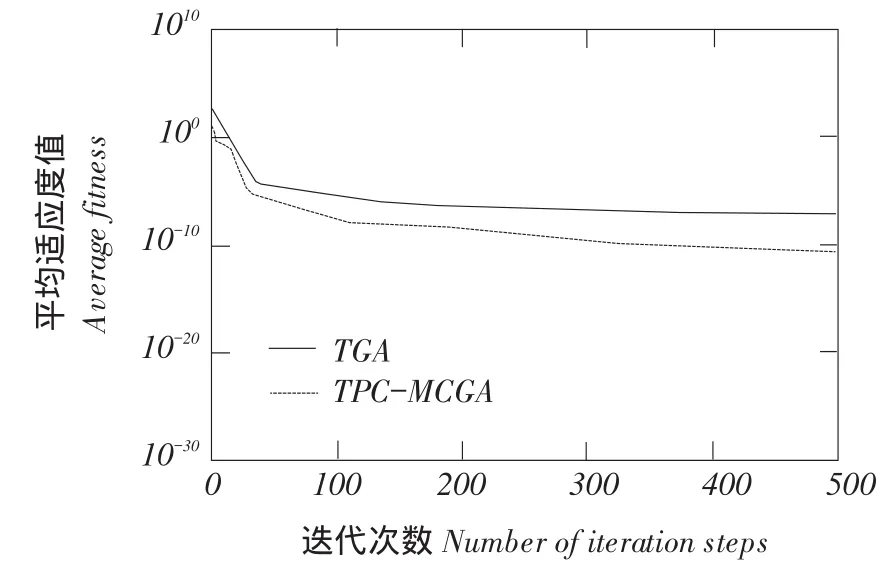
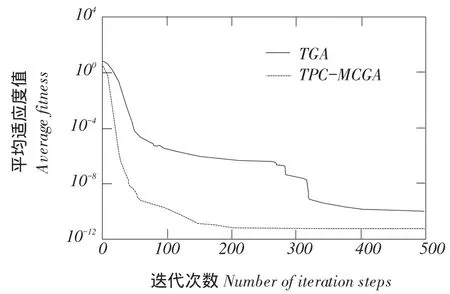
一对父代染色体在随机产生n(2 TPC-MCGA多子代个体产生方法见图1。 由图1可知,Child(ii=1,2,…,2Cn2)为交叉所产生第i个子个体。显然,在TPC-MCGA中,一对父代能够产生2Cn2个新子代个体,其子代个体数量是传统GACn2倍。例如,有被选择参与交叉两个父代个体P1和P2,采用二进制编码,其分别为P1= 1011001000和P2=1100110110,设产生随机交叉点个数n为3,假设这3个交叉点分别位于第3、6、8位,则有 交叉点:1 2 3 P1=101 100 10 00, P2=110 011 01 10 因此,父代个体P1和P2按图1所示两点交叉多子代产生方法得到子代个体分别为: C1=101 011 10 00, C2=110 100 01 10, C3=101 011 01 00, C4=110 100 10 10, C5=101 100 01 00, C6=110 011 10 10, 显然,TPC-MCGA中子代个体数量明显增加,子代中优秀个体产生概率升高,同时一对父代个体交叉产生了更多具有相同父代特征子代个体,增加了算法最优解周围搜索精度,提高算法局部搜索能力。因此与传统GA相比,TPC-MCGA具有更快收敛速度和更强寻优能力。但子代个体数量过多必然导致每迭代一次运算量增加,因此应该选取合适子代数量。关于TPC-MCGA算法最佳子代数量确定需进一步理论分析和试验研究,为验证TPC-MCGA优越性,本文将以两个父代交叉产生最少多子代个体为例(即两个父代交叉产生4个多子代个体)进行算法比较测试试验与分析。 图1 两点交叉多子代遗传算法子代产生方法Fig.1 Method of producing multi-child offspring in TPC-MCGA TPC-MCGA进化策略是:首先产生种群规模为N0初始种群,计算种群个体适应度;第二通过轮盘赌方式随机选择参与交叉个体,将被选中每对个体按两点交叉产生多子代方法交叉,并从交叉产生N1个多子代个体和N0个父代个体中选择m个具有最高适应度个体作精英保留;第三对交叉产生N1个多子代个体变异,并将m个精英个体与变异后N1个子代个体进行种群内部竞争,竞争过程中淘汰(N1+m-N0)个低适应度个体以保持种群规模不变,形成新种群;最后计算新种群个体适应度,判断是否满足迭代终止条件,如果满足,则停止迭代,如果不满足,则循环以上过程使种群继续进化,到满足终止条件为止。其进化策略如图2所示。 6.1试验方法与测试函数选取 为验证本文提出TPC-MCGA性能,选取6个常用典型测试函数[21-22],将TPC-MCGA与传统遗传算法(Traditional genetic algorithm,TGA)进行算法搜索性能对比试验。试验拟采用两种方法:固定搜索精度运算速度比较法和固定迭代次数求解精度比较法。 TPC-MCGA与TGA均采用二进制编码,初始种群随机产生,试验参数设置如下:种群规模N0= 100,子代个体数量与其父代个体数量比例系数α= 2,交叉概率Pc=0.9,变异概率Pm=0.1,保留精英个体数m=10,TPC-MCGA与TGA迭代终止条件为: 式中,fi*-第i个函数理论最优解;fi-算法搜索到第i个函数最优解;εi-第i个函数搜索停止精度。 6个测试函数搜索停止精度εi均为10-4。两种算法对每个测试函数在相同测试环境下分别独立运行1 000次。 所用6个测试函数包含多个已知极值点,有连续、非连续、单峰,多峰、病态等不同数学特征。 测试函数1: 图2 多子代遗传算法进化策略Fig.2 Evolution strategy ofTPC-MCGA 6.2试验结果与分析 由表1可知,TPC-MCGA与TGA算法对测试函数f1~f6固定搜索停止精度为10-4独立对比试验结果,其中平均迭代次数和平均计算时间是指算法运行1 000次对各测试函数符合迭代停止条件,即达到搜索停止精度平均迭代次数和平均计算时间。图3~8分别给出固定迭代次数为500时,两种算法对6个测试函数独立运行1 000次平均适应度收敛曲线。由表1可知,6个测试函数取得最优解时,TPC-MCGA平均计算时间0.3813~1.1250 s,平均迭代次数11.1185~39.2031次;TGA平均计算时间为0.5963~1.6231 s,平均迭代次数22.9530~ 78.7100次。与TGA相比,TPC-MCGA平均计算时间减少31%~36%,平均迭代次数减少50.2%~ 51.6%。显然,TPC-MCGA平均计算时间与平均迭代次数均明显优于TGA。这是由于在函数优化时,TPC-MCGA每次迭代产生子代个体数量多于TGA,因此子代种群规模要明显大于TGA,增加了子代中高适应度优秀个体概率。子代个体经过变异后,在种群竞争过程中大部分低适应度个体被淘汰,使在TPC-MCGA中生存子代个体平均适应度高于TGA,同时在进化策略中引入种群内部竞争操作,使子代种群规模与初始种群保持规模一致,保证种群在有限生存空间内加速进化。因此,TPCMCGA求解运算速度明显优于TGA。 由图3~8可知,与TGA算法相比,TPC-MCGA收敛精度明显提高。尤其对于测试函数f3和f6,经过少量次数迭代,TPC-MCGA即可达到理论最优值。这是由于一对父代产生了更多具有相同父代特征子代个体,增加算法在当前最优解周围搜索精度,提高算法局部搜索能力。 表1 TPC-MCGA与TGA算法测试结果Table 1 Testing results of TPC-MCGA and TGA 图3 函数f1平均适应度收敛曲线Fig.3 Convergence curve of average fitness for f1 图5 函数f3平均适应度收敛曲线Fig.5 Convergence curve of average fitness for f3 图7 函数f5平均适应度收敛曲线Fig.7 Convergence curve of average fitness for f5 图4 函数f2平均适应度收敛曲线Fig.4 Convergence curve of average fitness for f2 图6 函数f4平均适应度收敛曲线Fig.6 Convergence curve of average fitness for f4 图8 函数f6平均适应度收敛曲线Fig.8 Convergence curve of average fitness for f6 本试验结果表明,遗传算法子代数量增加提高了算法求解运算速度和收敛精度,与Hsieh等研究结果一致[23]。但在Hsieh研究中,将随机产生个体加入子代种群中提高子代数量,因此搜索效率提高依靠随机产生个体中出现优秀个体概率,本文采用两点交叉产生多子代个体方法,使产生多子代个体继承父代特征,保留父代个体优秀模式,提高子代出现优秀个体概率,结果表明,采用本文提出方法,搜索效率和收敛精度均明显提高。Shi等研究提出遗传算法个体生存概率概念,使每代个体均有一定概率生存到下一(几)代,因此子代数量增加,算法收敛加快,但后期过大种群规模导致运算效率降低,不适于处理复杂优化问题[24]。Koljonen等研究认为,种群规模增加提高遗传算法稳定性,但降低收敛速度[25]。本试验研究表明,通过引入种群内部竞争机制,增加子代群体通过竞争淘汰低适应度个体,保证种群在有限生存空间内加速进化,提高算法收敛速度。 本试验中选取子代个体数量与其父代个体数量比例系数α=2,即两个父代交叉产生4个多子代个体。结果显示,与TGA相比,TPC-MCGA平均计算时间与平均迭代次数均明显减少,证明TPCMCGA优越性,为解决目前遗传算法局部搜索能力差,运算速度慢,收敛精度低问题提供有效方法。由本试验结果可知,当取α=3时,TPC-MCGA平均计算时间与迭代次数进一步减少,但减少量小于α= 2时计算时间和迭代次数减少量,这表明α=2并不非最佳子代与父代个体数量比。显然,子代个体数量变化对TPC-MCGA性能有显著影响。虽然本试验证明TPC-MCGA求解精度与运算时间均优于TGA,但不能确定TPC-MCGA最佳子代数量,对TPC-MCGA子代个体数量对算法性能影响及变化规律需深入研究。针对如不同编码条件下TPCMCGA子代产生方法研究,TPC-MCGA子代数量与运算速度关系研究,种群规模对TPC-MCGA算法收敛精度影响等有待进一步探讨。 本文在研究传统遗传算法基础上,依据生物学和数学生态学理论,针对目前遗传算法局部搜索能力差、运算效率低问题提出两点交叉多子代遗传算法(TPC-MCGA),该算法利用两点交叉方式产生多于父代个体子代种群,使子代种群中出现优秀个体概率明显增加,提高算法寻优能力。该算法在进化策略中引入种群内部竞争操作,使多子代种群在有限生存空间内竞争,加快算法求解运算速度。本研究结果表明,TPC-MCGA在运算速度与求得最优解精度上均明显优于TGA算法。 [参考文献] [1]Sivanandam S N,Deepa S N.Introduction to Genetic Algorithm[M].New York:Springer-verlag Berlin Heidelberg,2008. [2]刘大莲,徐尚文.求解约束优化问题内外交叉遗传算法[J].系统工程理论与实践,2012,32(1):189-195. [3]Velkatraman S,Yen G G.A genetic framework for constrained optimization using genetic algorithms[J].IEEE Transactions on Evolutionary Computation,2005,9(4):424-435. [4]Holland J H.Adaptation in natural and artificial systems[M].Ann Arbor:University of Michigan Press,1975. [5]Tutkun N.Optimization of multimodal continuous functions using anew crossover for the real-coded genetic algorithms[J].Expert Systems with Applications,2010,36(4):8172-8177. [6]赵红杰,柏继云,马力.遗传扩展蚁群算法用于马斯京根模型参数估计[J].东北农业大学学报,2014,45(8):118-123. [7]Cheng T M,Yan R Z.Integrating messy genetic algorithms and simulation to optimize resource utilization[J].Computer- Aided Civil and Infrastructure Engineering,2009,24(6):401-415. [8]Liu C Y.An improved adaptive genetic algorithm for the multidepot vehicle routing problem with time window[J].Journal of Networks,2013,8(5):1035-1042. [9]杨世达,单志勇,李庆华.基于亲缘选择遗传算法[J].计算机工程,2009,35(15):10-12. [10]Zhang L,Cai L B,Li M,et al.A method for least- cost QoS multicast routing based on genetic simulated annealing algorithm[J].Computer Communications,2009,32(1):105-110. [11]Chen X,Wang N.Optimization of short-time gasoline blending scheduling problem with a DNA based hybrid genetic algorithm[J].Chemical Engineering and Processing,2011,49(10):1076-1083. [12]Wang K,Wang N.A protein inspired RNA genetic algorithm for parameter estimation in hydrocracking of heavy oil[J].Chemical Engineering Journal,2011,167(1):228-239. [13]徐梅,文士发,王福林,等.遗传算法求解约束优化问题时产生初始种群改进方法[J].东北农业大学学报,2014,45(7):104-107. [14]Saitoh A,Rahimi R,Nakahara M.A quantum genetic algorithm with quantum crossover and mutation operations[J].Quantum Information Processing.2014,13(3):737-755. [15]王福林,朱会霞,王吉权等.遗传算法一种改进进化策略[J].生物数学学报,2015,30(1):69-74. [16]李敏强,寇纪淞,林丹,等.遗传算法基本理论与应用[M].北京:科学出版社,2002:2-3. [17]Darwin C.On the Origin of Species by Means of Natural Selection[M].London:John Murry,1859. [18]Pielou E C.Mathematical Ecology[M].New York:John Wiley and Sons,1987:4-8. [19]Bailey N T.The Elements of Stochastic Procedures with Applications to the Natural Science[M].New York:John Wiley and Sons,1964. [21]王福林,朱会霞,王吉权.遗传算法一种改进进化策略[J].生物数学学报,2015,30(1):69-74. [22]王小平,曹立明.遗传算法-理论应用与软件实现[M].西安:西安交通大学出版社,2002:32-34. [23]Hsieh S T,Sun T Y,Liu C C.Potential offspring production strategies:An improved genetic algorithm for global numerical optimization[J].Expert Systems with Applications,2009,36(8):11088-11098. [24]Shi X H,Wan L M,Lee H P,et al.An improved genetic algorithm with variable population- size and a PSO- GA based hybrid evolutionary algorithm[C].International Conference on Machine Learningand Cybernetics,2003:1735-1740. [25]Koljonen J,Alander J T.Effects of population size and relative elitism on optimization speed and reliability of genetic algorithms[C].In Proceedings of the 12th Finnish Artificial Intelligence Conference,2006:26-27. Multi-child genetic algorithm based on two-point crossover WANG Fulin1,FU Xiaoming1,ZHU Huixia2,ZHAO Shengxue1(1.School of Engineering,Northeast Agricultural University,Harbin 150030,China; 2.School of Management,Liaoning University of Technology,Jinzhou Liaoning 121001,China) Abstract:Considering that current genetic algorithm had low efficiency in local extreme searching and low convergence accuracy,the two-point crossover multi-child genetic algorithm(TPC-MCGA)was proposed.The superiority of this algorithm was illustrated in theory.On this basis,the method of producing multi-child offspring was presented.This method not only improved the probability of creating excellent individuals with higher fitness,but increased searching accuracy around the current optimal solution so as to improve the local search ability of GA.In addition,since the internal competition operation was adopted in the evolution strategy,the population evolve increasingly in the limited living space which improved the convergence speed of GA.The results showed that the average computational time of TPC-MCGA was reduced 31% to 36% and the average iteration steps of TPC-MCGA was reduced 50.2% to 51.6% compared with TGA.The computational speed and the searched optimal solution accuracy of TPC-MCGA were increased obviously compared with traditional GA. Key words:multi-child genetic algorithm; two-point crossover; the quantity of children; evolution strategy 作者简介:王福林(1959-),男,教授,博士,研究方向为农业系统工程与管理科学与工程。E-mail:fulinwang1462@126.com 基金项目:国家自然科学基金(31071331);国家社会科学基金(13BJY098) 收稿日期:2015-12-06 中图分类号:TP301.6 文献标志码:A 文章编号:1005-9369(2016)03-0072-08
5 TPC- MCGA进化策略
6 试验与分析
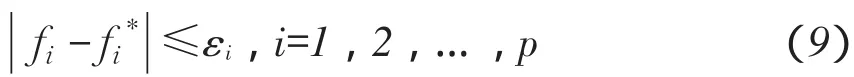


7 讨 论



8 结 论
