多变量时滞过程二自由度Smith预估控制方法



多变量时滞过程二自由度Smith预估控制方法

Internal model controlMaximum sensitivityParameters tuningChemical industry

0引言

在现代工业生产过程中，多变量时滞过程广泛存在。由于各回路之间的耦合作用，使得现在成熟的单变量控制方法很难直接应用到多变量过程中，因此，解耦控制的研究对多变量时滞过程具有重要的理论和实际意义。其中，反向解耦是目前化工过程中最常用的解耦方法。文献[1]通过比较，得出了反向解耦的优点，并对可实现性、稳定性和鲁棒性等方面进行了分析。文献[2]针对多变量时滞系统提出了两种反向解耦的控制方法，并运用内模控制原理设计了PI/PID控制器，取得了较好的控制效果。文献[3]提出了一种更简单、方便的反向解耦控制方法，且普遍适用于高维多变量系统。另外，考虑到Smith预估控制对于解决时滞问题的有效性，有很多学者将其应用到多变量系统中。文献[4]针对含有时滞以及右半平面零点的多变量过程，运用内模控制原理，设计了一种Smith解耦补偿控制器，增强了系统的鲁棒性和抗干扰能力。对于一阶时滞的非方系统，文献[5]利用内模控制方法，设计了Smith预估控制器，不仅能够动态地补偿静态解耦的缺陷，还克服了模型近似和不确定性带来的影响。文献[6]构造了一种多变量Smith预估控制结构，提出了基于多变量过程模型伴随矩阵的解耦器设计方法，并为解耦后的多变量时滞过程设计了PI控制器。然而，以上所提到的方法并不能很好地兼顾系统的设定值跟随特性和干扰抑制特性。为此，文献[7]～[8]分别针对开环不稳定的多变量时滞过程和非方系统，提出了一种二自由度控制器的设计方法，使系统的性能得到了显著提高。该方法虽然能够独立设计控制器，但仍然存在着计算复杂、整定参数多等缺点，并且不适用于高维多变量时滞过程。

因此，本文针对常见的方形多变量时滞过程，提出一种二自由度Smith预估控制的多变量解耦控制方法。根据反向解耦的方法，实现被控过程的完全解耦，并对解耦后的广义被控过程分别设计设定值跟随控制器和干扰抑制控制器。仿真结果证明了该方法的有效性和优越性。

1控制器的设计

二自由度Smith解耦控制结构如图1所示。

图1　二自由度Smith解耦控制结构图

图1中，G(s)为被控过程，K(s)为解耦控制器，Gp(s)为解耦后的广义被控过程，Gm(s)为广义被控过程的数学模型，Gm0(s)为Gm(s)不包含时滞的部分，Gc(s)为设定值跟随控制器，Q(s)为干扰抑制控制器，r(s)、y(s)和d(s)分别为系统的输入、输出和干扰。

由图1可得系统的输入与输出之间的关系为:

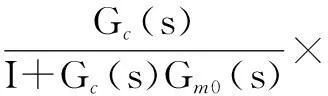
(1)

(2)

当模型精确，即Gp(s)=G(s) K(s)=Gm(s)时，有：

(3)

Gyd(s)=Gp(s)[I-Gm(s)Q(s)]

(4)

由此可知，设定值跟随特性只与Gc(s)有关，而干扰抑制特性只与Q(s)有关。因此，可以分别设计Gc(s)和Q(s)，使系统同时具有良好的设定值跟随特性和干扰抑制特性[9-10]。

1.1反向解耦控制器的设计

反向解耦控制器K(s)由Kd(s)和Ko(s)组成，其中Kd(s)为前向通道传递函数，Ko(s)为正反馈通道传递函数。对于n×n的多变量过程，Kd(s)应有n个非零元素，Ko(s)应有n个零元素，且Kd(s)中非零元素的位置与Ko(s)中零元素的位置互相转置。

K(s)的设计应使解耦后的过程模型为期望的对角矩阵形式，且在标称情况下：

Gp(s)=Gm(s)=diag[t1(s),…,tn(s)]

(5)

当模型精确，即G(s)K(s)=Gm(s)，且Gm(s)可逆时，有：

K-1(s)=Gm-1(s)G(s)

(6)

由反向解耦控制器k(s)的结构组成可得：

K(s)=Kd(s)[I-Ko(s)Kd(s)]-1

(7)

则：

Kd-1(s)-Ko(s)=Gm-1(s)G(s)

(8)

由式(8)可看出，Kd(s)必须非奇异，因此，Kd(s)的每行每列中应仅有一个非零元素。

对于n×n的多变量过程，如果Kd(s)每行依次选择p1，p2，…，pi，…，pn列为非零元素，则Kd(s)和Ko(s)的非零元素可分别由式(9)和(10)得出。

(9)

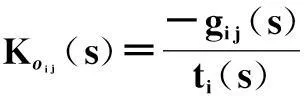
(10)

另外，若G(s)中存在时滞或右半平面零点，则K(s)不可实现。在这种情况下，应在G(s)前添加对角矩阵N(s)[11]，构成一个新的被控过程Gn(s)=G(s)N(s)，以使得K(s)可实现，进而设计Kd(s)和Ko(s)。N(s)中对角元素nii(s)的表达式为：

(11)

式中：λii为滤波器参数;mii为保证G(s)第i列元素可物理实现的阶数;z为G(s)第i列元素中存在的右半平面(right half plane, RHP)零点;rii为同一RHP零点的最大个数;qii为G(s)第i列元素存在qii个不同的RHP零点;θii为G(s)第i列元素含有的最大时滞。

1.2设定值跟随控制器的设计

解耦后，期望的系统通常为一阶加时滞过程和二阶加时滞过程。

(12)

(13)

式中：T为过程时间常数；K为过程增益；L为时滞时间。针对上述两类过程，根据Dahlin控制算法，可将设定值跟随特性设计为：

(14)

则设定值跟随控制器分别为：

(15)

(16)

对应的PI和PID控制器参数分别为：

1.3干扰抑制控制器的设计

为了使系统获得良好的干扰抑制特性和鲁棒性[12]，Q(s)采用内模控制方法进行设计。对于一阶加时滞过程，选择滤波器f(s)=(αs+1)/(λ′s+1)2，其中，λ′是滤波器时间常数，α为待定系数。根据式(2)，确定α使(1-GmQ)的零点对消Gp(s)中的极点，则可以改进干扰抑制性能，即:

(17)

则:

α=T[1-(1-λ′/T)2e-L/T]

(18)

干扰抑制控制器Q(s)为:

(19)

式中:Gm-(s)为模型Gm(s)中的最小相位部分。

对于二阶加时滞过程，选择滤波器f(s)=1/(λ′s+1)2，则干扰抑制控制器为:

(20)

在以上所设计的干扰抑制控制器中，参数λ′是唯一的可调参数，且与系统的鲁棒性直接相关。

2控制器参数的整定

在过程控制中，系统的模型往往是不精确的，而且随着控制条件和时间的变化，模型的参数也会发生变化。因此，系统的鲁棒性是需要考虑的重要因素[13-14]。最大灵敏度Ms作为反馈控制系统中的一个有效的鲁棒性能指标，其定义如下：

(21)

式中:L(j)为控制系统开环传递函数的频率特性;Ms的取值范围一般为1.2～2.0，其值越小，系统的鲁棒性越好[15-16]。

当模型精确时，对与一阶加时滞过程和二阶加时滞过程相对应的系统开环传递函数分别为:

(22)

(23)

可以根据灵敏度定义来实现参数λ′的整定。

3仿真研究

例1：考虑精馏塔模型[17]。

(24)

选取与文献[17]同样的期望传递函数，即:

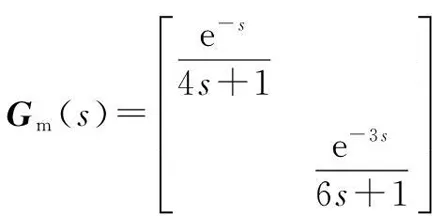
(25)

根据式(9)和式(10)得:

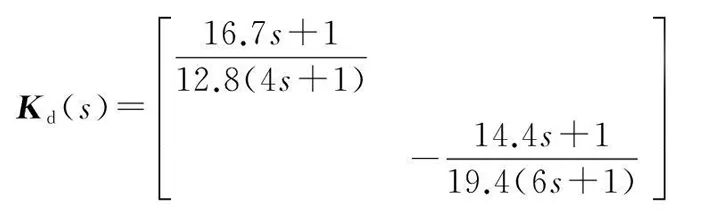
(26)

(27)

在本文的方法中，分别取λ为4和6，从而得到与文献[8]方法相同的设定值响应速度；根据式(15)、式(16)得PI控制器参数， 分别为Kp1=1，Ti1=4；Kp2=1，Ti2=6。

整定参数λ′时，最大灵敏度函数Ms分别取为1.7和1.22。根据式(19)，得干扰抑制控制器：

Q(s)=

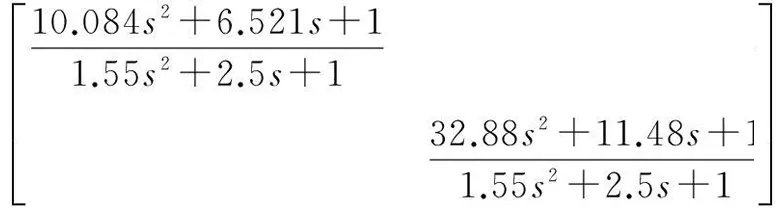
(28)

分别在t=0时和t=50s时，加入幅值为1的阶跃输入信号，并在t=100s时加入幅值为-0.1的阶跃输入干扰信号。y1和y2的输出响应曲线如图2所示。

图2　标称情况下输出阶跃响应曲线图

分析曲线可知，该系统在达到完全解耦的同时，也具有良好的控制效果。与文献[17]相比，本文的方法具有更好的动态特性和抗干扰特性。

为了验证系统的鲁棒性，被控过程的各传递函数的增益、时间常数和滞后时间均增大20%。在模型摄动情况下，系统输出的响应曲线如图3所示。与文献[17]相比，本文的方法具有更强的鲁棒性。

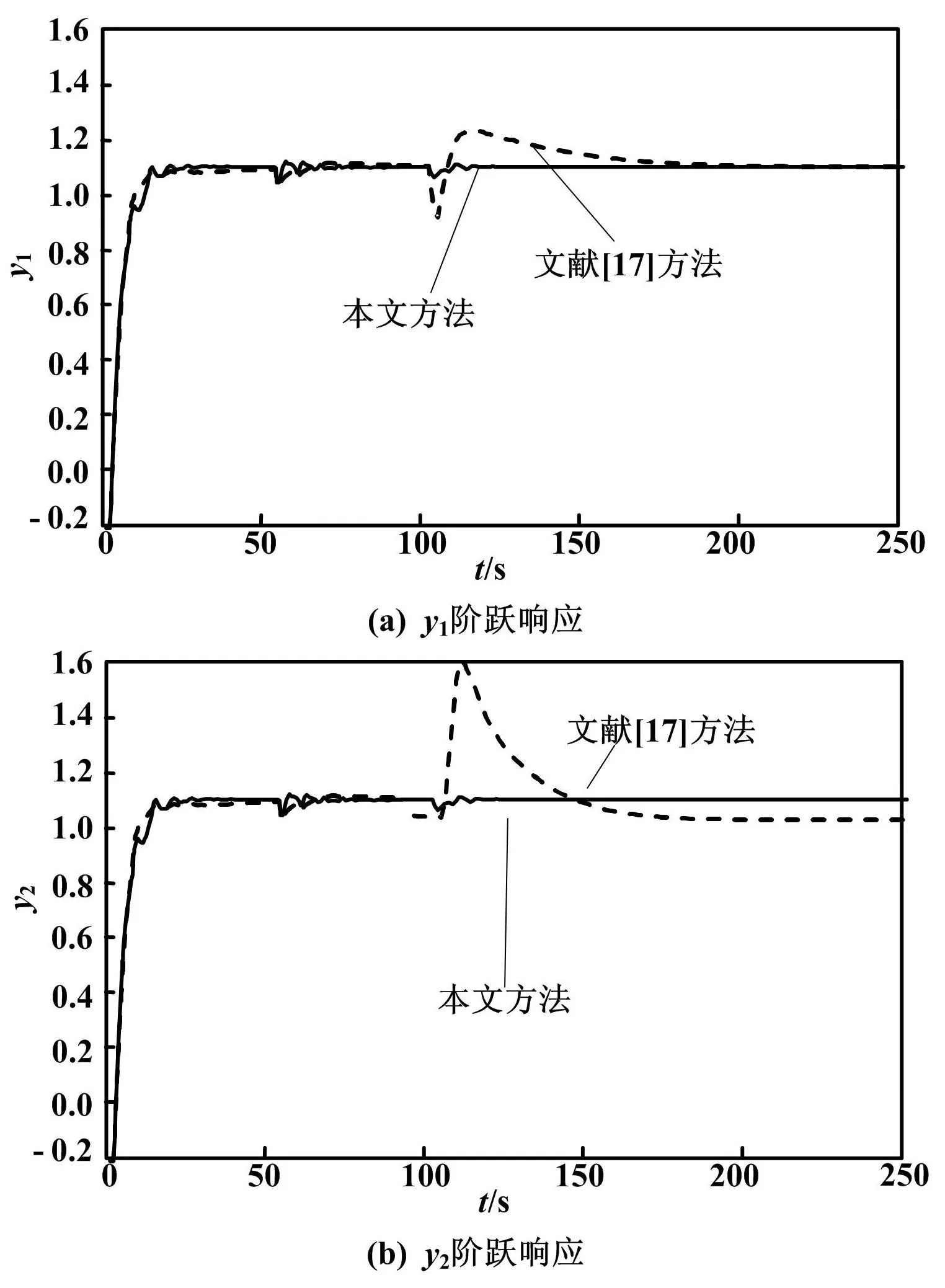
图3　摄动情况下输出的阶跃响应曲线

例2：考察文献广泛研究的3×3化工蒸馏塔

过程[18]。

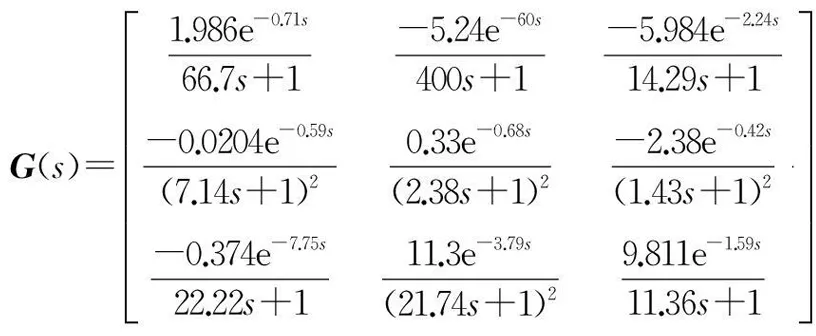
(29)

由于时滞的原因，不宜设计反向解耦控制器。因此，根据式(11)，得添加的对角矩阵为：

(30)

则新的被控过程传递函数为：

Gn(s)=

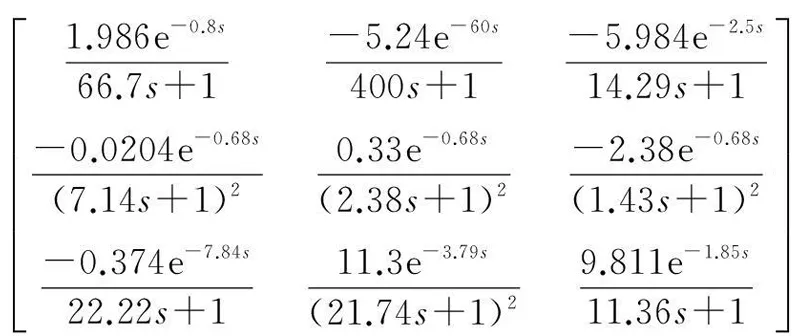
(31)

将本文的方法与文献[18]中的方法进行比较。选取同样的期望传递函数，即：

(32)

根据式(9)和式(10)，得：

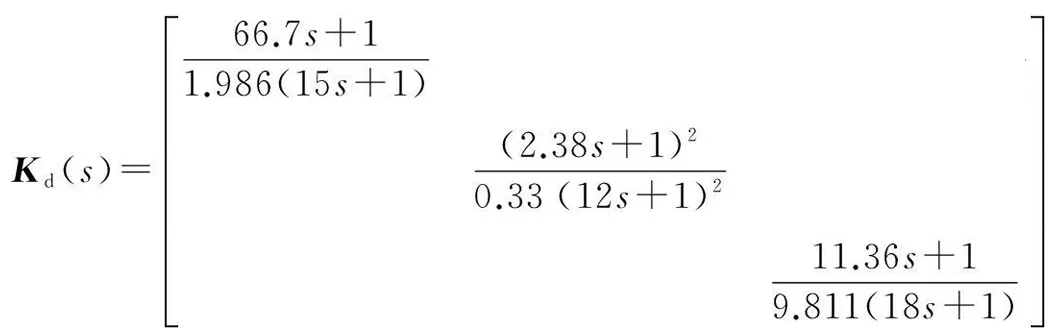
(33)

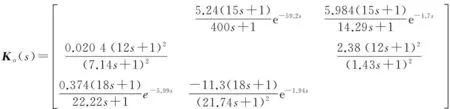
(34)

为了比较的公平性，使得本文与文献[18]所提方法的设定值响应速度基本相同，分别取λ为15、18和18；根据式(15)和式(16)，得PI和PID控制器参数分别为Kp1=1，Ti1=15；Kp2=1.3，Ti2=24，Td2=6；Kp3=1，Ti3=18。

整定参数λ′时，最大灵敏度函数Ms分别取为1.3，1.28和1.21，根据式(19)和式(20)得干扰抑制控制器：

(35)

对r1、r2和r3,分别在t为0s、200s和400s时,加入幅值为1的阶跃输入信号;在t为600s时,加入幅值为-0.2的阶跃输入干扰信号。3个回路的输出响应y1、y2和y3如图4所示。

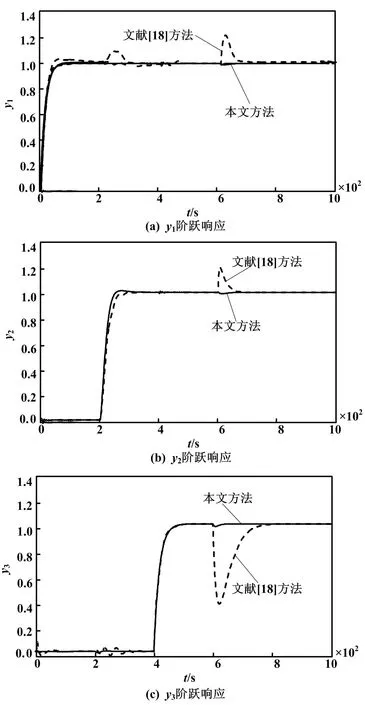
图4　标称情况下输出阶跃响应曲线图

由标称情况下的输出响应可以看出：本文方法的输出响应基本实现了完全解耦，动态特性好；相比文献[18]的方法，有更强的干扰抑制特性。

为了验证本文方法的鲁棒性，将控制过程的静态增益和惯性时间常数均增大40%，摄动情况下系统阶跃响应如图5所示。由摄动情况下的输出响应曲线可知：本文方法在模型摄动时的曲线与标称情况下基本相同，与文献[18]相比，有更好的鲁棒性。

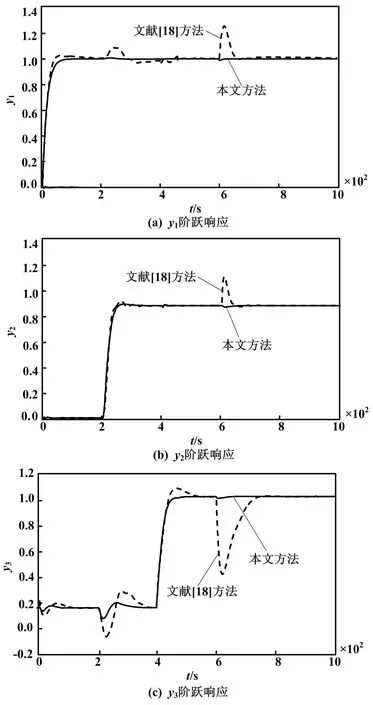
图5　摄动情况下输出阶跃响应曲线图

4结束语

本文通过构造多变量二自由度Smith解耦控制结构，提出一种反向解耦控制器的设计方法，能够实现标称系统输出响应之间的完全解耦。该方法对于高维多变量时滞过程也有很好的适用性。对期望解耦后的过程，分别运用Dahlin控制算法和内模控制的方法，设计设定值跟随控制器和干扰抑制控制器，并基于最大灵敏度实现干扰抑制控制器参数的整定。仿真结果表明了该方法的有效性和优越性。

参考文献

[1] Wade H L.Inverted decoupling: a neglected technique[J].ISA transactions,1997,36(1): 3-10.

[2] Chen P,Zhang W.Improvement on an inverted decoupling technique for a class of stable linear multivariable processes[J].ISA transactions,2007,46(2): 199-210.

[3] Garrido J,Vázquez F,Morilla F.Inverted decoupling internal model control for square stable multivariable time delay systems[J].Journal of Process Control,2014,24(11): 1710-1719.

[4] Guo M,Peng Y.The control method of multivariable time-delay square system containing right half plane zeros[J].Procedia Engineering,2011(15): 1004-1009.

[5] Chen J,He Z F,Qi X.A new control method for MIMO first order time delay non-square systems[J].Journal of Process Control,2011,21(4): 538-546.

[6] 黄灿,桂卫华,阳春华,等.多变量时滞过程解耦Smith控制[J].控制理论与应用,2010,27(10):1393-1398.

[7] Liu T,Zhang W,Gu D.Analytical design of two-degree-of-freedom control scheme for open-loop unstable processes with time delay[J].Journal of Process Control,2005,15(5): 559-572.

[8] Liu J C,Chen N,Yu X.Modified two-degrees-of-freedom internal model control for non-square systems with multiple time delays [J].Journal of Harbin Institute of Technology,2014,2(21)：122-128.

[9] Liu T,Zhang W,Gao F.Analytical two-degrees-of -freedom(2-DOF) decoupling control scheme for multiple- input-multiple-output(MIMO) processes with time delays[J].Industrial & Engineering Chemistry Research,2007,46(20): 6546-6557.

[10]Huang H P,Lin F Y.Decoupling multivariable control with two degrees of freedom[J].Industrial & engineering chemistry research,2006,45(9): 3161-3173.

[11]Garrido J,Vázquez F,Morilla F.Centralized multivariable control by simplified decoupling[J].Journal of Process Control,2012,22(6): 1044-1062.

[12]Xie L B,Shieh L S,Pan F,et al.Design of decoupling and tracking controllers for continuous-time transfer function matrices with multiple time delays[J].Journal of Process Control,2014,24(1): 152-170.

[13]Vijay Kumar V,Rao V S R,Chidambaram M.Centralized PI controllers for interacting multivariable processes by synthesis method[J].ISA transactions,2012,51(3): 400-409.

[14]Sánchez-Pena R S,Bolea Y,Puig V.MIMO Smith predictor: Global and structured robust performance analysis[J].Journal of Process Control,2009,19(1): 163-177.

[15]赵志诚,刘志远,张井岗.一种积分时滞过程的内模PID鲁棒整定方法[J].华中科技大学学报:自然科学版,2012,39(12):72-75.

[16]Rao A S,Chidambaram M.Smith delay compensator for multivariable non-square systems with multiple time delays[J].Computers & Chemical Engineering,2006,30(8): 1243-1255.

[17]刘涛,张卫东,欧林林.双输入输出时滞过程解耦控制的解析设计[J].控制理论与应用,2006,23(1):31-37.

[18]刘涛,张卫东,顾诞英.多变量时滞过程的解耦控制设计[J].自动化学报,2006,31(6):881-889.

Two Degree of Freedom Smith Predictive Control for Multivariable Process with Time-delay

雷帅赵志诚张井岗

(太原科技大学电子信息工程学院，山西 太原030024)

摘要：针对工业系统中普遍存在的多变量时滞过程，提出了一种二自由度Smith预估控制的方法。通过在被控过程前串联反向解耦矩阵，实现标称系统的完全解耦。在此基础上，运用Dahlin控制算法和内模控制方法，对解耦后的过程分别设计了设定值跟随控制器和干扰抑制控制器，并基于最大灵敏度实现了干扰抑制控制器参数的鲁棒整定。仿真结果表明：该方法设计简单、整定方便，而且具有良好的跟踪特性、抗干扰特性和鲁棒性。

关键词：多变量时滞过程二自由度Smith预估控制反向解耦控制器内模控制最大灵敏度参数整定化工

Abstract：For the multivariable processes with time delay that commonly exist in industrial systems,the two degree of freedom Smith predictive control is proposed.The complete decoupling of nominal system can be achieved through connecting the reverse decoupling matrix prior to the controlled process.On this basis,by adopting Dahlin control algorithm and internal model control method,the set-point tracking controller and disturbance suppression controller are designed respectively for the decoupled process,and the robust tuning for the parameters of disturbance suppression controller is implemented based on maximum sensitivity.The results of simulation show that the proposed method is simple in design convenient in parameter tuning,and possesses excellent tracking performance,anti-disturbance capability,and robustness.

Keywords:Multivariable process with time-delayTwo degree of freedomSmith predictive controlInverted decouplingController

中图分类号：TP273+.3;TH86

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201604008

山西省回国留学人员科研基金资助项目(编号：2013-092);

晋城市科技计划基金资助项目(编号：201501004-3)。

修改稿收到日期：2015-05-26。

第一作者雷帅(1990-)，男，现为太原科技大学控制科学与工程专业在读硕士研究生；主要从事先进控制及应用的研究。