一种舰载机下滑道一致性指示数据产生方法

王兆毅,刘爱东,高　波,杜亚杰

(海军航空工程学院,山东烟台　264001)



一种舰载机下滑道一致性指示数据产生方法

王兆毅,刘爱东,高波,杜亚杰

(海军航空工程学院,山东烟台264001)

摘要:针对现有航母起降引导系统下滑道真值测量手段过于复杂的现状,提出一种简单的航母起降引导系统下滑道一致性指示数据产生方法,该方法基于着舰引导雷达测距精度、中线电视测角精度较高的特点,利用着舰引导雷达测距信息和中线电视测角信息进行目标位置解算。采取泰勒级数展开法对非线性方程组线性化,并以着舰引导雷达定位结果作为迭代始值,进行迭代运算求取目标位置。通过仿真实验验证该方法迭代次数较少且收敛,相比着舰引导雷达定位方法,具有更高的定位精度。

关键词:泰勒级数展开法;定位;均方根误差;标校

目前,国内外航母海上校飞真值测量手段有多种,但一般都相对复杂[1-2],为了对真值测量设备性能进行校验或者在不具备其它高精度真值测量设备的条件下为舰载机着舰下滑道一致性提供指示数据,本文提出利用起降引导系统内具有较高测距精度的着舰引导雷达和较高测角精度的中线电视联合对舰载机进行跟踪定位。

着舰引导雷达、中线电视两站联合定位,是基于测角、测距空间定位原理,在考虑测量误差的基础上,建立非线性方程组求解得到目标位置结果的。非线性方程组求解问题,利用解析法并不容易实现,一般将问题转化为非线性优化的最优估计问题,其中泰勒级数展开法[3-5]适用于任何定位方法,且原理简单,能获得较好的位置精度;但是泰勒级数展开法会由于迭代初值的选取不同导致可能出现不收敛或收敛到局部最优的情况[6],基于此,本文提出以着舰引导雷达定位结果作为迭代始值,利用泰勒级数展开法进行目标位置解算,经过与着舰引导雷达定位方法的定位精度作对比,表明本文的方法具有定位精度高的特点,实用性强。

1两站联合定位

两站联合定位过程其特征基本包括三个步骤:

1)基于着舰引导雷达高精度的测距和测角特征,建立着舰引导雷达单站空间定位模型,并对目标位置进行初步定位;

2)对着舰引导雷达实时测量数据进行预处理,并对预处理后的数据与中线电视数据进行时空统一;

3)建立两站联合定位数学模型,并对目标位置进行最终解算。

基于以上步骤,本文将分别进行分析。

1.1着舰引导雷达单站定位模型

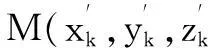
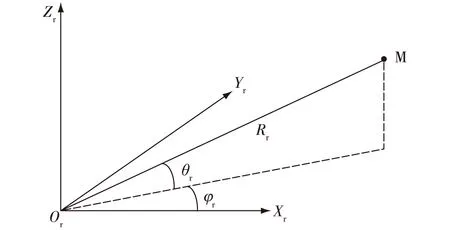
图1　着舰引导雷达单站定位示意图

根据观测量Rr、φr、θr,由图1可以直接得到对目标位置的解算，有

(1)

1.2坐标系转换

两站联合定位方法采用的基准坐标系与中线电视坐标系重合,即以中线电视回转中心为坐标原点Oc,Xc轴与甲板中线重合,指向舰艉方向;Yc轴平行于甲板面,与Xc轴垂直,指向航母右舷;Zc轴与Xc轴、Yc轴构成右手直角坐标系。由于着舰引导雷达坐标系和基准坐标系均为甲板固连坐标系,因此着舰引导雷达在基准坐标系下的位置坐标是固定的,设目标在基准坐标系中的位置坐标为M(xk,yk,zk)T,中线摄像机在基准坐标系中的位置坐标为Oc(xc,yc,zc)T,着舰引导雷达在基准坐标系中的位置坐标为Or(xr,yr,zr),两站联合定位模型示意图如图2所示。

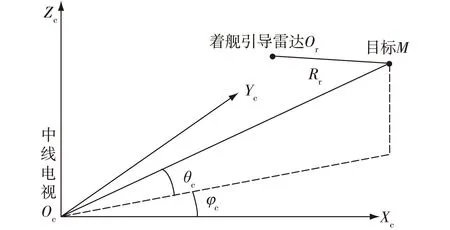
图2　两站联合定位示意图

基准坐标系和着舰引导雷达坐标系相对位置如图3所示。

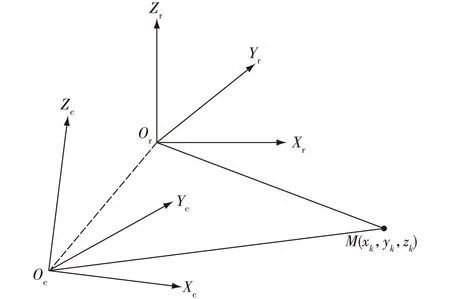
图3　坐标系转换示意图

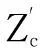
(2)

1.3两站联合空间定位求解

在图2坐标系中,目标相对中线摄像机的方位和俯仰坐标分别为:

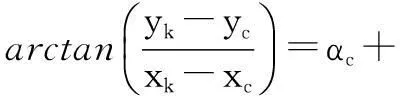
(3)

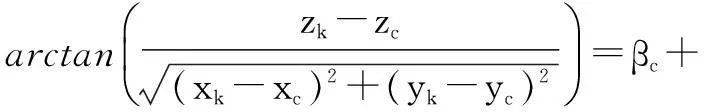
(4)

式中，αc、βc分别表示中线电视测得的目标相对于自身的方位角和俯仰角;1、2分别表示中线电视方位角、俯仰角测量误差。

目标到着舰引导雷达的距离为

(5)

式中:Rr为着舰引导雷达测得的目标距雷达的距离,3为着舰引导雷达距离测量误差。

根据式(3)、(4)、(5),可以得到一组关于目标位置的非线性方程组,方程组中着舰引导雷达和中线电视坐标已知,测量值可以实时录取,测量误差分布规律可根据设备统计规律获取。

式(3)的一阶展开为

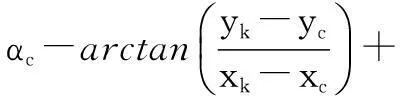
(6)

应对此进行加权处理：将其乘以目标到中线摄像机在XcOcYc平面投影线长度[8],即

(7)

式(4)的一阶展开式为

(8)

同样对此进行加权处理：将其乘以目标到中线摄像机的距离,即

(9)

式(5)的一阶展开为

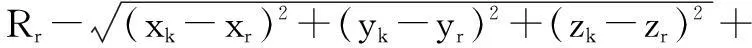
(10)

将上述运算写成矩阵形式:

(11)

(12)

(13)

式中,

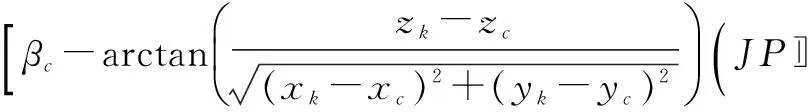
(14)

可将式写成为

Hδ≈z+

(15)

根据误差协方差矩阵进行加权处理,使平方和误差最小的δ为

δ=[HTY-1H]-1HTY-1z

(16)

其中,Y必须是正定满秩的。

这样,在一次迭代中,δ可根据式(16)进行计算,通过

(17)

得到新的解算值。重复迭代直至相邻两次迭代中(xk,yk,zk)的变化达到充分小为止。

迭代终止的判据不同,选择的门限的大小不同,通用的判据主要有以下几种:

(18)

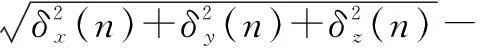
(19)

ε=max(|δx(n+1)|,|δy(n+1)|,|δz(n+1)|)

(20)

ε=max(|δx(n)-δx(n+1)|,

|δy(n)-δy(n+1)|, |δz(n)-δz(n+1)|)

(21)

在本文中,判断迭代是否终止与着舰引导雷达的测距精度和中线电视的测角精度有关,设着舰引导雷达的测距精度为εr,中线电视的方位角测角精度为εcα,俯仰角测角精度为εcβ,则门限可以选取应满足距离、角度误差小于相应精度的1/3,可表达为

(22)

2定位精度分析

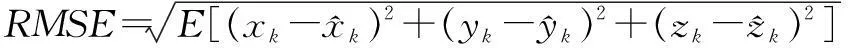
(23)

在实际应用中,由于观测次数有限,因此可以用多次测量观测值与真值偏差的平方与观测次数比值的平方根代替。

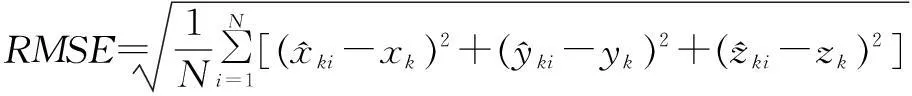
i=1,2,…,N

(24)

式中N为MonteCarlo仿真次数。

均方根对一组测量中的特大或特小误差反映非常敏感,所以能较好地反映出不同定位方法的定位精度[10]。

3算法仿真分析

假设在基准坐标系下中线电视的坐标为(xc,yc,zc)T=(0,0,0)T,着舰引导雷达的坐标为(xr,yr,zr)T=(90,-15,11)T,以上单位均为m。着舰引导雷达测距误差服从均值为0,标准差为1.7m的正态分布,测角误差服从均值为0,标准差为0.06°的正态分布;中线电视方位角测角误差服从均值为0,标准差为0.001°的正态分布,俯仰角测角误差服从均值为0,标准差为0.035°的正态分布,且各测量误差之间相互独立。本文仿真假设目标按照理想下滑道4°的下滑角模拟舰载机进行着舰,从目标的Xc轴坐标值为5180m开始,到180m为止,每隔200m进行数据采集来模拟目标从距理想着舰点5km处开始沿理想下滑道着舰的过程,在每个采集点进行次数10000次的蒙特卡洛仿真分析,即N=10000,选取式(22)作为迭代终止判据。

在只考虑中线电视和着舰引导雷达测量误差的情况下,着舰引导雷达单站定位方法和两站联合定位方法的均方根误差随着目标位置变化的关系仿真结果如图4所示。两种方法随着目标位置不同定位精度关系及两站联合定位方法平均迭代次数如表1所示。

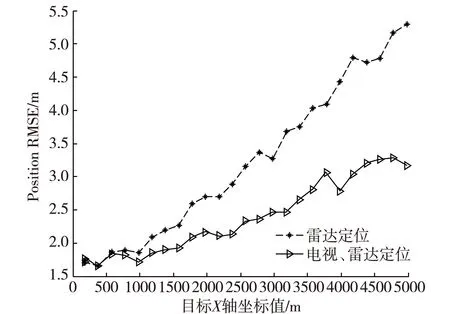
图4　两种方法均方根误差分布图

仿真结果表明,由于着舰引导雷达可以提供较高精度的目标位置信息作为迭代初始点,两站联合定位方法平均不超过两次就能实现迭代收敛,且解算结果与目标真实值误差不大;在目标距理想着舰点150m以内时,两种方法均方根误差基本一致,但两站联合定位方法定位误差较大,是因为算法本身在泰勒级数展开时舍去二阶以上误差分量导致精度有所损失,随着目标距理想着舰点距离越远,两种方法定位均方根误差均逐渐扩大,算法本身导致的定位误差相比测量设备性能误差导致的定位误差已微乎其微,两站联合定位方法相比着舰引导雷达测距/测角定位方法精度优势越明显。

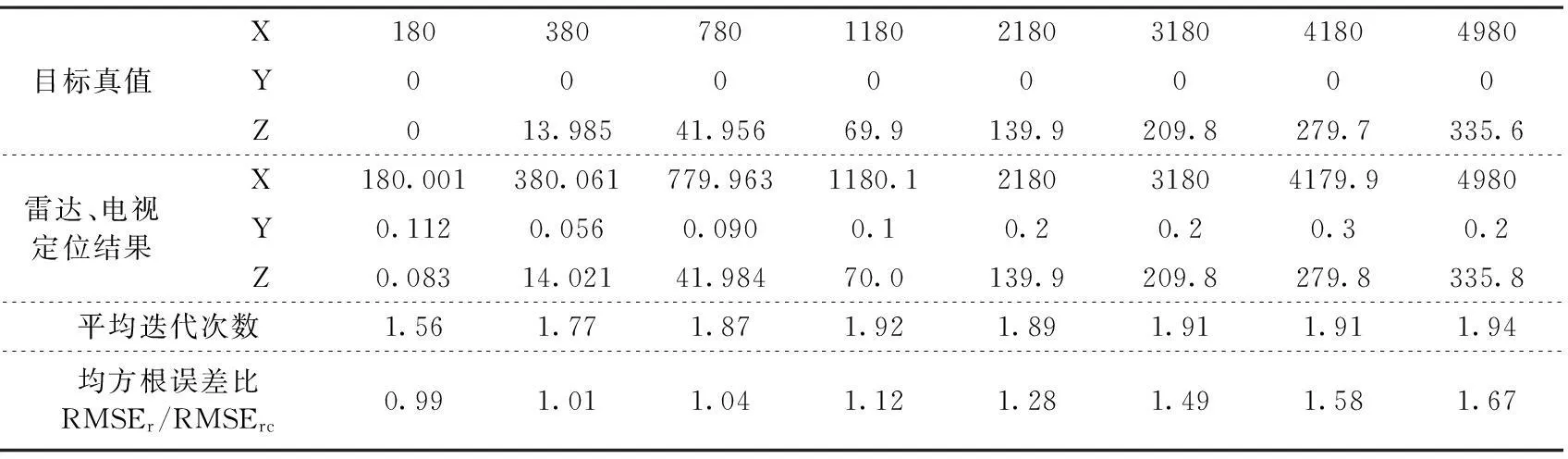
表1两站联合定位结果

4结束语

根据以上分析,可以看出利用两站联合定位方法的优点为:以着舰引导雷达定位结果为迭代初始点,初始点距目标真实值较近,迭代收敛性较好,相比着舰引导雷达测角/测距空间定位方法精度更高,并且由于中线电视可以通过网络实时接收雷达的测距信息并通过时间戳存储同一时刻自身测角信息,在时间统一上非常方便,对于后期数据处理可以节省很大的时间成本,且可以大大简化标校保障条件。缺点为:在近距离条件下,定位精度与着舰引导雷达单站定位精度相差不大,且由于算法缘故导致定位精度有一定损失,另外,相比其他真值测量手段,由于中线电视和着舰引导雷达本身测量精度限制,只能对系统下滑道一致性提供粗略比对,要进行更高精度的下滑道一致性标校,需采用更高精度测量设备。

参考文献:

[1]Robert L F. Practical Integration of Direct Lift Control into an Automatic Carrier Landing System. AIAA-92-7103[R]. [S.l.]: AIAA, 1992:60-69.

[2]段静玄,等. 基于全球定位系统的舰载三坐标雷达动态标校方法[J].中国舰船研究,2012,17(4).101-103.

[3]Foy,W.H.Position-Location Solutions byTaylor-Series Estimation[J].IEEE Transactions on Aerospace and Electronic Systems,1976,12(2):187-193.

[4]李莉,邓平,刘林.Taylor级数展开法定位及其性能分析[J].西南交通大学学报,2002,37(6):684-688.

[5]D.W.Marquardt.An algorithm for least-squares estimation of nonlinear parameters[J].J.Soc.Ind.Appl.Math,1963,11(2):31-41.

[6]邢永丽,陈建春.泰勒级数在近似计算中的应用[J].湘潭师范学院学报(自然科学版),2004(1).

[7]田孝华,周义建.无线电定位理论与技术[M].北京:国防工业出版社,2011:46-47.

[8]李相民,孙瑾,谢晓方.火力控制原理[M].烟台:海军航空工程学院出版,2005.

[9]Richard A.Poisel.电子战目标定位方法[M].王沙飞,田中成,译. 北京:电子工业出版社,2014:3-8.

[10]Kegen Yu,Ian Sharp,Y.Jay Guo.Ground-Based Wireless Positioning[M].北京:电子工业出版社,2012.

A Instruction Date Generating Method of Aircraft Carrier Glide Path Consistency

WANG Zhao-yi,LIU Ai-dong, GAO Bo,DU Ya-jie

(Naval Aeronautical Engineering Institute, Yantai 264001, China)

Abstract:In accordance with the current situation that there are limited means to get the true value in the process of the calibration of taking-off and landing system,this paper presents a new method to generate the taking-off and landing system slope indicator data. Based on the characterisitics that the ranging information the radar mesures and the angle information the middle line camera mesureds own higher accuracy,the method estimates the position with the ranging information. and the angle information. It chooses the solution by Taylor-Series Estimation to straighten the nonlinear equations,then solves the equations,then obtains the target position by iterative calculation.The simulation result indicates that the iteration constricts and it is less often.Through the comparison with the single radar location, the solution which the paper used owns higher position-location accuracy.

Key words:Taylor-Series estimation; positioning-location; RMSE; calibration

中图分类号:TJ630.3+4；E917

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.02.018

作者简介：王兆毅(1992-),男,河南洛阳人,硕士研究生,研究方向为武器系统与运用工程。刘爱东(1968-),男,教授,硕士生导师。杜亚杰(1991-),男,博士研究生。

收稿日期：2016-01-18

文章编号：1673-3819(2016)02-0084-05

修回日期： 2016-02-26

高波(1975-),男,副教授。