基于动态窗口的灰色加权填充算法及应用*

王　泽,程　恺,董　坤,王家腾

(解放军理工大学指挥信息系统学院仿真与数据中心,江苏南京　210007)



基于动态窗口的灰色加权填充算法及应用*

王泽,程恺,董坤,王家腾

(解放军理工大学指挥信息系统学院仿真与数据中心,江苏南京210007)

摘要:为解决复杂系统中单属性缺失数据填充困难问题,提出了基于动态窗口的灰色加权填充算法。该算法通过建立双向灰色预测模型,并采用模型精度评价系数加权填充缺失数据,有效增强了算法的准确性;提出基于灰色模型评价系数反馈的动态伸缩窗口概念,寻找产生最优模型的训练数据序列,使算法具有良好的鲁棒性和适应性。实验结果表明,该方法在RMSE和MA两项指标上均优于传统的双向灰插值、灰插值、多项式插值等方法。

关键词:动态窗口;灰色预测;加权系数;缺失值填充;军事训练数据

在现实数据分析挖掘中,数据缺失是一个普遍存在的现象:广泛用于机器学习的UCI基准数据库有接近40%的数据集存在数据缺失问题[1-2];在军事训练演习数据中,几乎每一个数据表格都存在不同程度的数据缺失[3]。导致缺失现象的原因很多,如设备故障、输入丢失等,如果不对缺失值进行处理或者处理不充分,得出的分析结果会存在偏差或得出的模型不具备普遍性[4-6],缺失数据填充已然成为了一项必不可少的数据预处理技术。

缺失值填充方法包括简单填充、属性填充和实例填充三种类型,本文主要研究属性填充方式。属性填充依赖原始数据的单一或少量属性维度,利用属性间的关系或属性潜在的规则对缺失值进行填充。常用的属性填充方法有:基于回归分析[7]、信息增益[8]、灰色预测[9-10]的方法和EM算法[6]等。基于回归分析的填充方法通过拟合回归数学模型计算缺失值,该方法仅适用于满足确定数学模型的数据集;基于信息增益的方法，依据与缺失数据关联密切的属性对缺失值进行填充,该方法针对标称型数据效果良好，但不适用于数值型数据;序列缺失数据的灰插值推理方法通过引入灰色预测模型拟合单属性函数,插值填充缺失值,取得了良好的效果,然而该算法限制了训练模型,可伸缩性不强;基于EM模型的填充方法认为数据服从含参分布,算法经过多次迭代收敛填充缺失数据,得到的填充效果良好但迭代方式很大程度地加大了算法复杂性,限制了方法的实际应用。

军事训练演习数据产生于训练演习系统中的各个要素,由于训练演习信息系统十分庞大,是典型的复杂系统,产生的数据具有多源性、关联性和动态性等特征[11-12]。军事训练演习数据的缺失值填充存在两方面问题亟待解决,首先复杂系统各属性数据之间的关系尚不明确,其次某些属性数据的相关要素无法采集或不能量化,因此大量依赖相关属性的缺失值填充方法无法满足这一特殊背景。

综上所述,为满足算法性能需求和特定应用背景,本文针对灰色系统中单属性数据缺失问题,提出基于动态窗口的灰色加权填充方法,通过建立滑动窗口双向灰色预测模型,对缺失数据进行加权填充,增强算法准确性;提出基于灰色模型评价反馈的动态窗口概念,优化灰色模型累加数列,改善算法的鲁棒性。

1相关基础理论

1.1灰色预测模型GM(1,1)[10]

设原始数据序列为:x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),累加序列为x(1)=(x(1)(1),x(1)(2),…,x(1)(n)),其中x(1)(t)为前几项数据之和:

(1)

建立关于x(1)(t)的一阶线性微分白化方程:

(2)

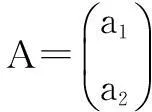
通过最小二乘法求解参数向量A,得

(3)

将式(3)得出的结果代入式(2),并对微分方程求解可得

(4)

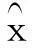
(5)

1.2灰色模型评价指标

灰色模型的评价指标包括三种:相对误差q,方差比C,小误差概率P。相对误差q是原始值与预测值的残差与原始值之比,反映了预测值与原始值的偏离程度,计算公式如式(6):

(6)

方差比C表示残差序列的方差与原始数据方差之比,设原始数据序列均值为μ(0),残差序列均值为μ(q),则

(7)

小误差概率P表示残差小于残差序列方差的概率,如式(8):

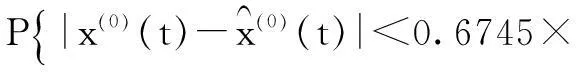
(8)

2基于动态窗口的灰色填充方法

基于动态窗口的灰色填充方法首先找到数据序列中缺失值的位置;之后根据缺失值所在位置设定初始填充窗口,并建立双向灰色预测模型;然后动态调整窗口大小,使得模型达到一定步长范围内的最优;最后根据最优双向预测模型得到的结果对缺失数据进行预测填充。具体概念和步骤如下。

2.1双向灰色预测模型

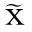
图1　窗口示意

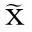
2.2动态窗口模型

双向预测模型较大程度地提高了算法的填充精准度,然而在没有先验知识帮助下难以确定窗口步长大小,而不同步长的数据序列产生的模型预测效果差别明显,因此固定的窗口步长限制了算法的应用。针对这一问题,本文提出动态窗口概念,使用灰色模型精度检验指标作为反馈系数,动态调整左右窗宽,改善算法的鲁棒性和适应性。

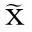
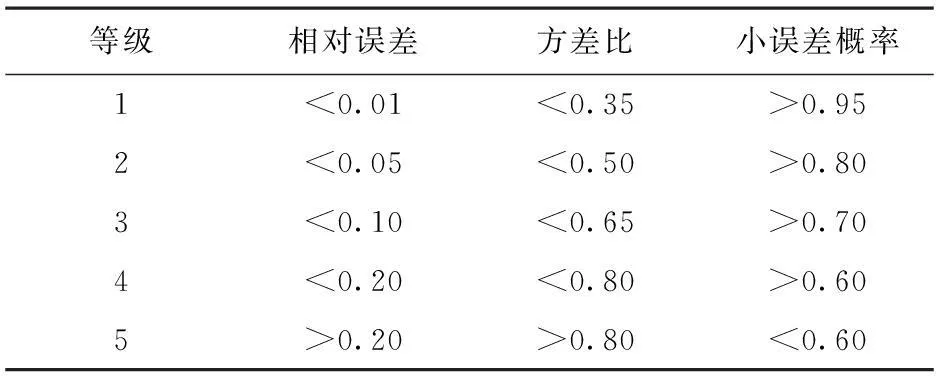
表1　灰色模型精度检验表[10]

2.3加权系数

由双向灰色预测模型得到的结果包括前向预测结果和后向预测结果,而不同的模型训练数据会产生不同的预测结果,若对两个预测值进行简单的综合,不具备说服力且效果不理想。本文针对这一问题,对两个预测模型得到的结果采用反馈系数加权策略,以提高算法准确性。

(9)

本文基于模型的拟合程度越高,得到的预测结果越精确这一原则,并根据精度综合考虑模型贡献程度,提出组合系数λ的计算方法:

(10)

其中,ε表示前后灰色模型共同保存的比例,al表示前向预测模型精度的等级,ar表示后向预测模型精度的等级。式(10)既考虑了前后向模型的精准程度,又有效防止了过拟合现象。

2.4算法过程及复杂度分析

基于动态窗口的灰色填充方法具体步骤如下:第一步,找到数据序列内中缺失值所在位置;第二步,在缺失值前后定义初始窗口;第三步,针对窗口内前后向序列分别采用动态窗口模型调整步长,直到找到最优双向预测模型出现;第四步,在最优窗口基础上得到加权预测值作为填充值。算法流程图如图2所示。

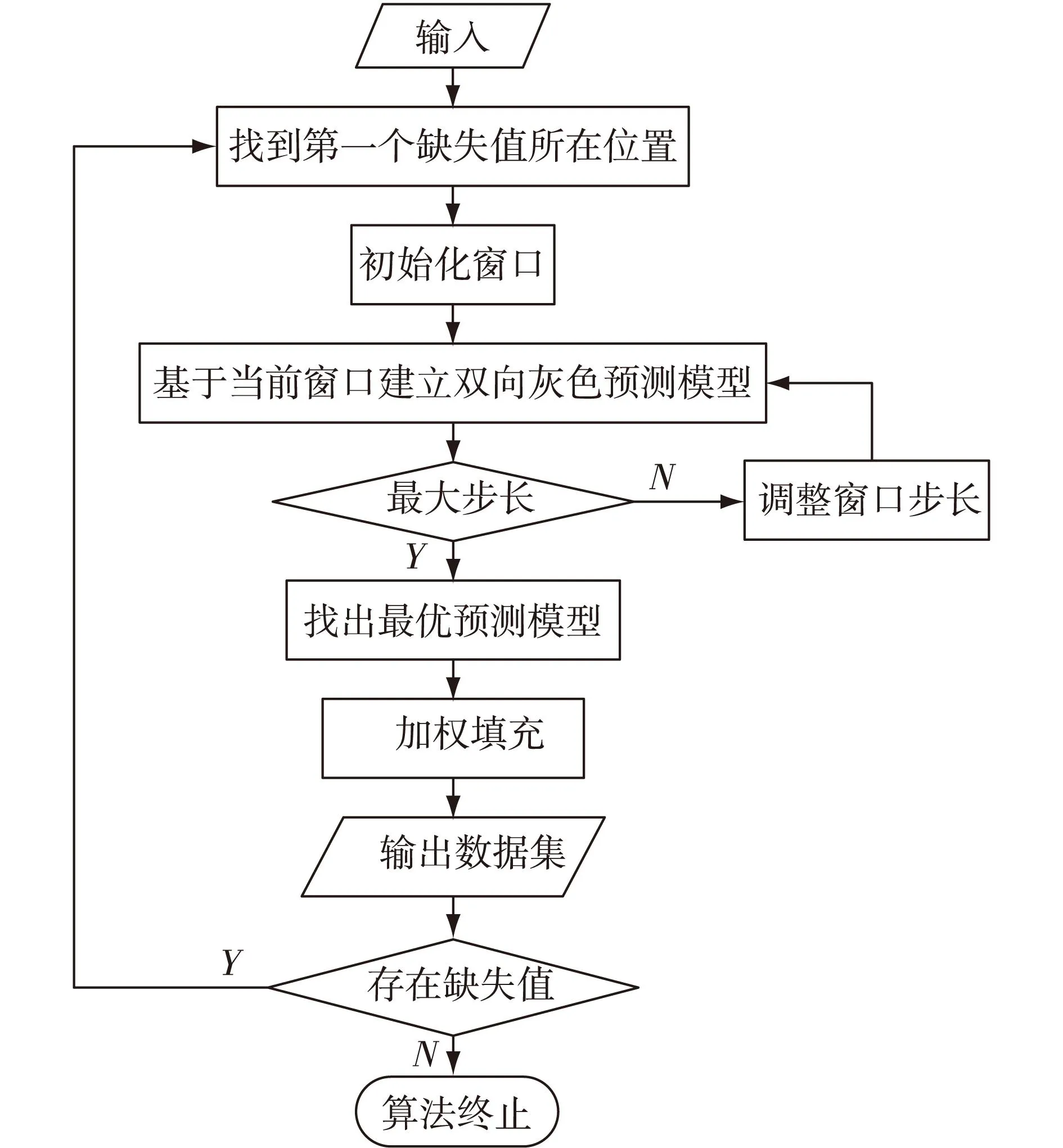
图2　算法流程图

算法存在两次循环,即寻找缺失值和调整窗口步长,设步长变化为常数C(最大步长与最小步长之差),则时间复杂度为:O(Cn);算法的模型建立在矩阵运算的基础上,矩阵运算的开销为1,因此算法的总时间开销为O(Cn),其中C≪n。与其他属性填充方式相比较,本文算法处于优势地位。

3实验与结果分析

实验运行环境:CPU为CORE i7,内存为8G,系统为Windows 7,算法运行工具为Matlab 2012a。分别在多个军事训练演习数据集上使用本文算法、多项式插值、灰插值、双向灰插值[9]等四个算法进行性能测试,并做出对比分析。

3.1评价指标

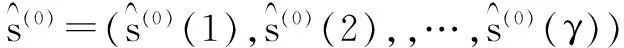
(11)

(12)

当填充效果越好时,RMSE的值越小,同时MA越接近于1。

3.2数据集说明

为验证算法的可行性与有效性,本文使用军事训练演习数据库中,某模拟器材在仿真战场演习环境中某时段的瞬时机动速度数据(Instantaneous velocity,IV)和某网关在某时段的信息流量数据(Gateway traffic,GT)作为实验数据。图3(a)表示IV数据集,横坐标为117个时间采样点,纵坐标表示在某一时刻的瞬时速度;图3(b)表示GT数据集,横坐标为4628个时间采样点,纵坐标表示在某一时刻的单位流量。

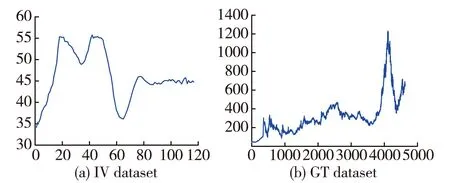
图3　数据集图示

对两个数据集的特征描述如表2,在军事训练演习信息系统中,机动速度和网关流量两个数据集均为单属性数值型时序数据,与其相关的要素多而复杂,而且从表中可以发现数据的波动十分大,GT数据集的离散系数达到了62.86%,因此很难使用某一种确定的模型来准确地预测填充缺失数据。

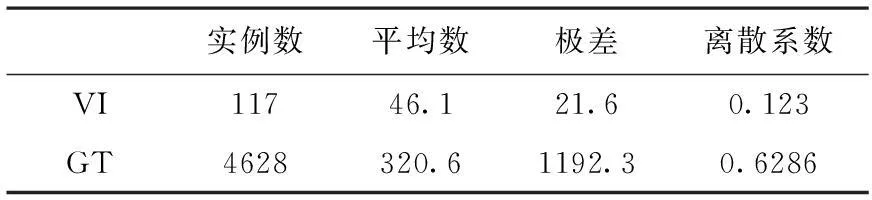
表2　数据集特征

3.3实验结果比较分析

3.3.1不同数据集上的对比实验

为验证算法针对不同特征数据集的适应性,本文针对IV数据集,随机选取6个时间采样点数据作为缺失数据,并分别使用本文算法、双向灰插值、灰插值、多项式插值等方法进行填充。在实验参数选取上,本文算法设置最大窗口为20,其余方法均设置窗口大小为16,得到的实验结果如表3所示。针对GT数据集,本文随机选取20个时间采样点数据作为缺失数据,设置窗口大小为30并采用同样的方式对缺失数据进行填充,得到的实验结果如表3所示。

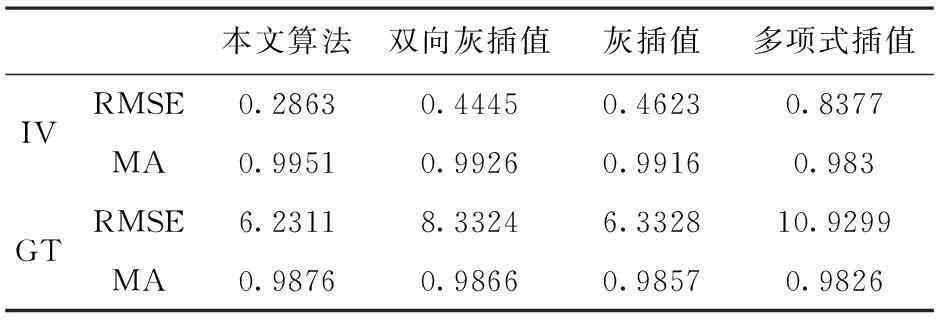
表3　实验结果

表2显示了四种不同属性填充方法对两个时序数据集的填充效果,不论是小型的阶段性序列数据还是大量序列数据,本文算法在均方根误差和平均填充精度两个评价指标上都优于其余方法。图4显示了原始数据图像(蓝色线条)与本文算法填充的单个数据点(红色“+”形状)的对比,从图中可以看出填充的数据几乎与原始数据一致。分析数据和实验结果,本文使用典型复杂系统中的单属性数据,难以确定数据趋势中的数学模型,且存在波动大而频繁的现象,符合灰色模型的使用范围。同时通过动态调整训练窗口大小,使用双向加权预测,使得预测模型更加准确,故能得到很好的填充效果。

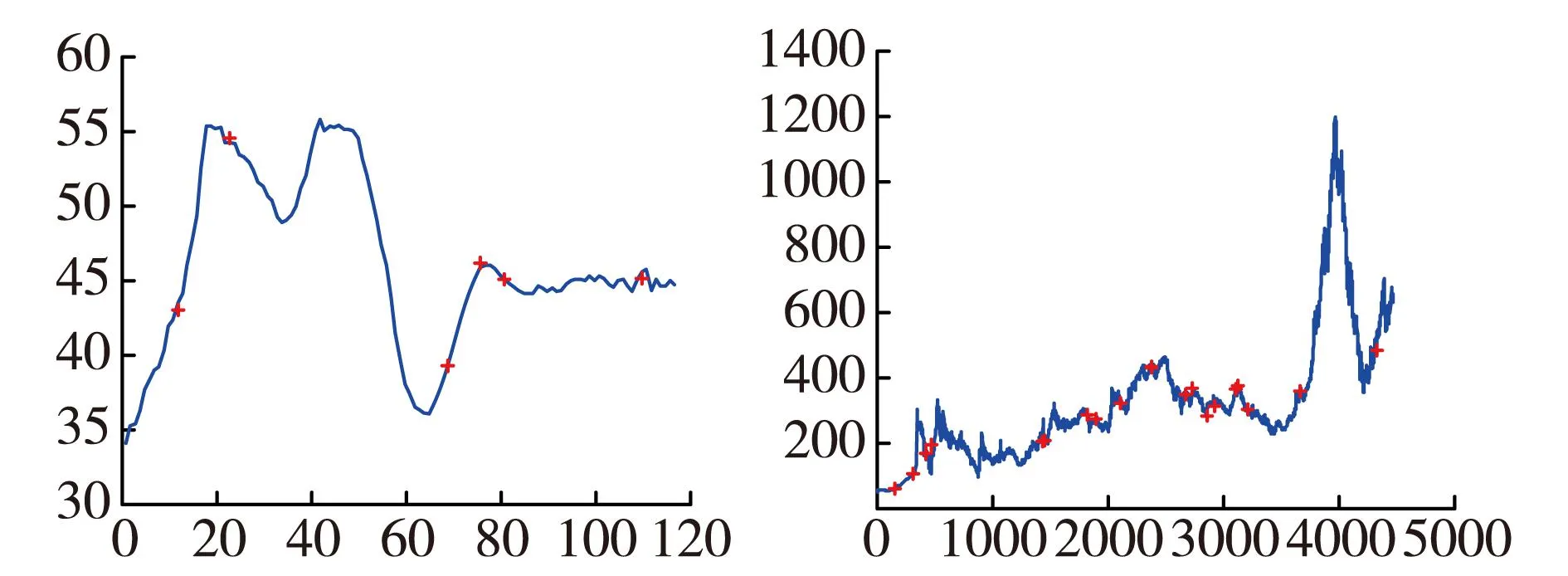
图4　填充数据与原始数据对比

3.3.2同一数据集上不同缺失率的对比实验

为验证算法对不同缺失比例的适应性,本文针对含有4628个时间采样点的数据集GT,分别选取5%,15%,25%,35%的数据作为缺失数据,在实验参数选取上,与上文一样。得到实验结果如图5所示。

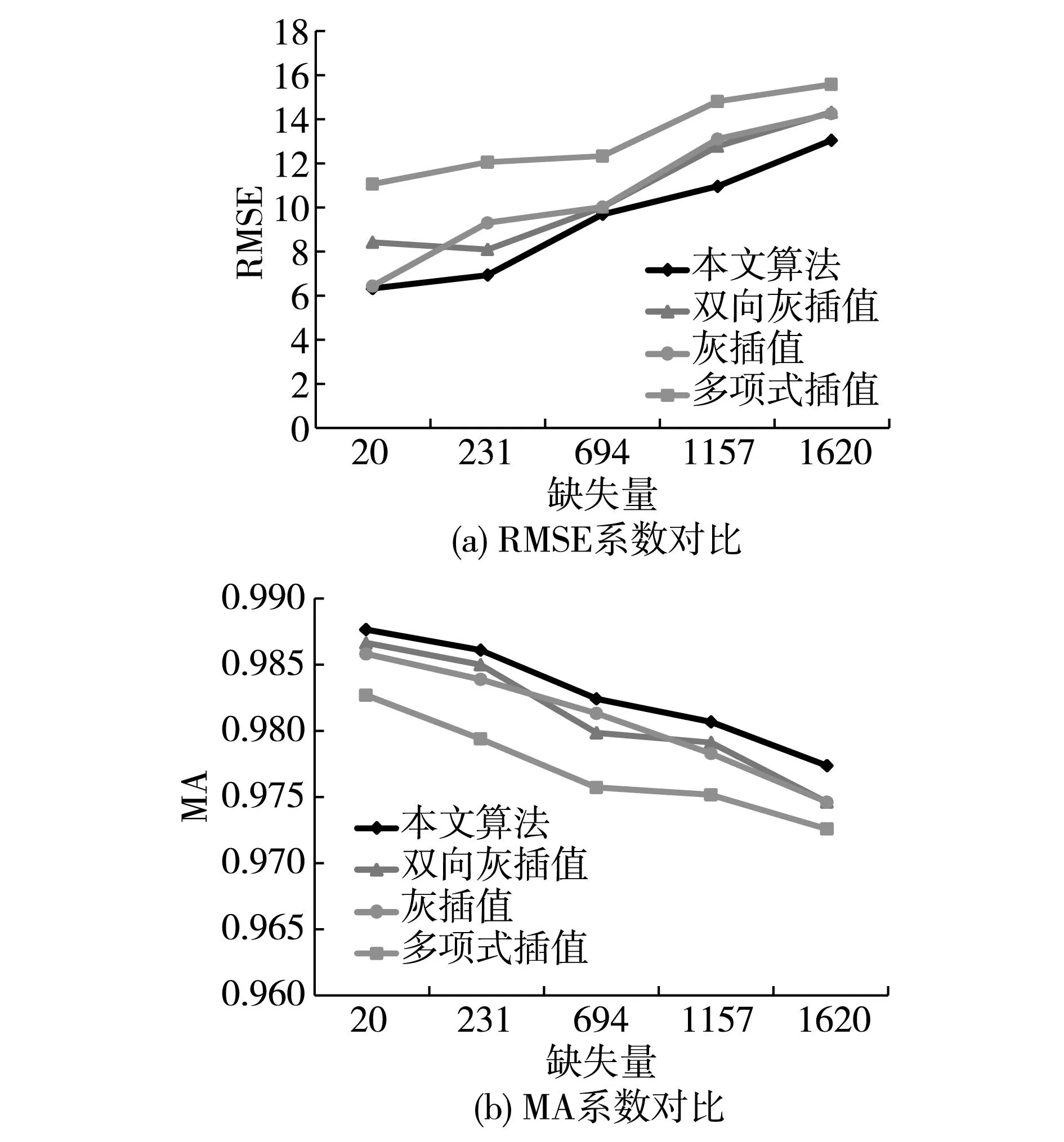
图5　针对不同缺失比例数据集的实验效果

图5(a)展示了四种不同算法对不同缺失比例数据集填充效果的RMSE评价指标对比,图5(b)则展示了MA评价指标的对比。从图中可以得出以下几点结论:随着数据集缺失比例的提高,各类型算法的填充效果都会降低;灰色填充的整体效果明显优于多项式填充,原因在于数据波动性较大,难以寻找一个准确的数学模型来拟合数据发展趋势;本文算法在综合了动态伸缩窗口和双向加权填充方法的条件下,效果明显优于其余方法;同时图中出现了一个有趣的现象,在含有694个缺失点的条件下,单向灰色预测效果优于双向预测,原因在于右侧数据的波动对双向预测产生了不良影响,但是在大多数情况下,双向预测模型效果更好。

4结束语

本文提出了一种基于动态窗口的双向灰色加权填充算法。该方法建立了双向灰色预测模型,通过前后向灰色模型的精度指标加权填充缺失数据,在提高填充准确度的同时制效避免了过拟合现象;提出基于灰色模型评价反馈的动态窗口方法,通过寻找最优窗口提高预测模型的准确性,有效改善了算法的鲁棒性和适应性。

应用实验表明,算法具有较优的性能,能够适应波动大、趋势不明显、缺失率高的单属性缺失数据;同时算法时间复杂度低,能够面临大数据集的压力。然而,算法没有充分利用属性间关系,针对属性关系密切的数据填充效果达不到最佳,如何将属性间关系综合到动态窗口的灰色加权模型中来,是下一步的努力方向。

参考文献:

[1]武森, 冯小东, 单志广. 基于不完备数据聚类的缺失数据填补方法[J]. 计算机学报, 2012, 35(8):1726-1738.

[2]García-Laencina P J, Sancho-Gómez J L, Figueiras-Vidal A R, et al. K nearest neighbours with mutual information for simultaneous classification and missing data imputation [J]. Neurocomputing, 2009, 72(s 7-9):1483-1493.

[3]张宏军, 郝文宁. 基于作战行动的训练演习实况数据编辑方法[J]. 军事运筹与系统工程, 2013, 27(3):10-14.

[4]Wu, X:Knowledge Acquisition From Database[M].Ablex Publishing, 1995.

[5]Han J, Kamber M, Pei J. Data mining: concepts and techniques (third edition)[M]. Morgan Kaufmann Publishers, 2012.

[6]García S, Luengo J, Herrera F. Data Preprocessing in Data Mining[M]. Springer International Publishing, 2015.

[7]Cooper L G, Leeuw J D, Sogomonian A G. An imputation method for dealing with missing data in regression[J]. Applied Stochastic Models & Data Analysis, 1991, 7(3):213-235.

[8]张红霞. 缺失值填充:基于信息增益的方法[J]. 计算机工程与设计, 2006, 27(24):4810-4812.

[9]金义富, 朱庆生, 邢永康. 序列缺失数据的灰插值推理方法[J]. 控制与决策, 2006, 21(2):236-240.

[10]邓聚龙. 灰预测与灰决策[M]. 武汉：华中科技大学出版社, 2002.

[11]胡晓峰. 战争复杂系统建模与仿真[M]. 北京:国防大学出版社,2005.

[12]张宏军,等.作战指挥训练模拟系统[M].北京：解放军出版社,2011.

[13]Zhang S, Jin Z, Zhu X. Missing data imputation by utilizing information within incomplete instances[J]. Journal of Systems & Software, 2011, 84(3):452-459.

Grey Weighted Imputation Method Based on Dynamic Window and Its Application

WANG Ze, CHENG Kai, DONG Kun, WANG Jia-teng

(Center of Simulation &Data, Institute of Command and Information System,PLA University of Science and Technology, Nanjing 210007, China)

Abstract:In order to solve the difficulty of single attribute missing values imputation in complex systems, a grey weighted imputation algorithm based on dynamic window is proposed. The algorithm imput missing values with two-way grey prediction model and model accuracy evaluation coefficient weighting method, which enhanced the algorithm precision effectively. It introduces a dynamic flexible window concept based on grey model evaluation coefficient feedback for finding the optimal model, which makes the algorithm be robust and adaptable. Numerical experiments results show that comparing several existing method, the algorithm can achieve better performance on root-mean-square error and mean accuracy.

Key words:dynamic window; grey predict; weighted coefficient; missing value imputation; military training data

中图分类号:TJ630.3+4；E917

文献标志码:A

DOI:10.3969/j.issn.1673-3819.2016.02.010

作者简介：王泽(1991-),男,湖南长沙人,硕士研究生,研究方向为模式识别和数据挖掘。

*基金项目：江苏省自然科学基金(BK20150720)

收稿日期：2016-01-08

文章编号：1673-3819(2016)02-0043-05

修回日期： 2016-02-27

程恺(1983-),男,博士,讲师。

董坤(1992-),男,硕士研究生。

王家腾(1991-),男,硕士研究生。