基于跟踪精度控制的多传感器管理方法
2016-05-04黎子芬程江涛欧阳寰
黎子芬,程江涛,欧阳寰
(海军航空工程学院青岛校区,山东青岛 266041)
基于跟踪精度控制的多传感器管理方法
黎子芬,程江涛,欧阳寰
(海军航空工程学院青岛校区,山东青岛266041)
摘要:针对地面机动目标跟踪过程中的多传感器管理问题展开了研究,设计了一种基于跟踪精度控制的多传感器多目标分配方法。首先,在考虑目标与目标之间、目标与传感器之间和传感器与传感器之间等的多种约束条件下运用基于协方差控制的思想建立了多传感器多目标分配问题的优化模型;接着将等价伪量测的异步融合算法与IMM算法结合,计算各目标在不同融合周期的跟踪精度估计值;最后,以目标的跟踪精度需求为出发点,结合蚁群算法的思想,设计了一种求解所建立的多传感器多目标分配问题的优化模型的算法。仿真结果表明:该管理方法能在确保跟踪精度需求的前提下,根据对各目标跟踪任务的重要程度,合理地调度传感器资源。
关键词:传感器管理;交互多模型;地面机动目标;异步数据融合;蚁群算法
在现代战争中,地面目标的机动能力越来越强,单传感器的跟踪能力很难满足对这类目标的跟踪需求,通过组织多个传感器构建传感器网络,并采用多传感器信息融合技术实现对这类目标的跟踪是一种现实可行的方法。
在多传感器管理方法中,基于信息增量的管理方法是一类常用的方法,这类方法的主要缺点是难于精确控制特定目标的跟踪精度[1],当传感器资源不足时可能会导致某些任务的需求得不到满足[2],而最早由M.Kalandros提出的基于协方差控制的传感器管理方法能克服这一缺陷。本文选择通过基于协方差控制的思想解决多传感器多目标的跟踪问题。在多传感器管理方面的研究主要集中在对匀速直线运动目标的跟踪上,如文献[3-5]。本文根据多传感器管理问题的实际约束条件建立了问题的优化模型,借鉴文献[6]中对异步信息的处理方法对多个传感器的测量数据进行处理,运用交互多模型算法对地面机动目标的运动状态进行估计,最后结合蚁群算法的思想设计了本文研究的多传感器多目标分配问题的求解算法。
1传感器分配问题优化模型
1.1数学模型
对于涉及跟踪精度的传感器资源管理问题,通常采取基于协方差控制[7]的策略来分配传感器资源。这一策略的基本思想是根据系统为每个目标预先设定的期望跟踪精度与实际跟踪精度之差来控制传感器资源的分配,使实际跟踪精度在某种意义上逼近期望精度。
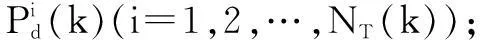
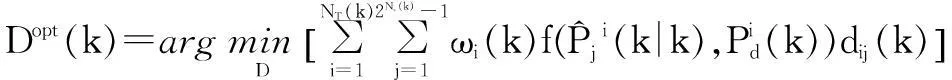
(1)
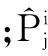
1.2约束条件
在传感器管理过程中,需要考虑实际条件的约束。为了方便对多传感器分配问题应满足的约束条件进行数学描述,下面对一些参量做如下假设。
STk表示为传感器(组)Sk分配的目标集合;
J(j)表示包含基本传感器j的所有传感器(组)构成的集合;
j→i表示基本传感器j具备监视目标i的能力;
j|→i表示基本传感器j不具备监视目标i的能力;

j↔j′表示基本传感器j与j′不能同时使用;
lj表示基本传感器j可同时监视目标的最大数量。
这些约束条件具体包括[8-9]:
1)传感器与目标之间的非匹配性。某些传感器不适合观测识别某些目标,那么包含该传感器的传感器组也不适合观测这些目标。如光电传感器,它的近距观测效果很好,在实际使用过程中,一般不用它观测远距离的目标。这一条件的数学描述为
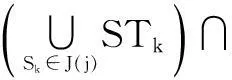
2)目标与目标之间的非兼容性。两个目标与某传感器,三者之间的相对位置使得该传感器对其中一个目标进行观测时不能观测另一个目标。如单面相控阵雷达的观测角度范围为120°,如果一个目标的方位角为0°,另一个为180°,那么该相控阵雷达不能同时观测这两个目标。这一条件的数学描述为
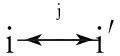
3)传感器与传感器之间的非兼容性。有些传感器之间在同时使用时会相互影响,那么由这些传感器构成的组合没有意义。如ESM不能与SAR或ESA同时使用。这一条件的数学描述为
j↔j′⟹j∉Sk,(Sk,∈J(j′)),且j′∉Sk(Sk∈J(j))
4)传感器的容量约束。为每个传感器分配的目标数量不能超过其能同时监视的最大目标数。这一条件的数学描述为
5)传感器(组)与目标的映射关系约束。一个目标只能分配给一个传感器组。这一条件的数学描述为
STk∩STk′=∅
2多传感器资源管理算法
2.1基于交互多模型的多传感器系统描述
交互式多模型(Interacting Multiple Model, IMM)算法是一种基于Kalman滤波器的算法,最初由Blom和Bar-Shalom提出[10-11]。交互多模型算法是目前公认的混合随机模型状态估计的最有效的方法之一。多传感器多模型系统的动态描述为:
X(m,tk)=Φ(m,tk|tk-1)X(m,tk-1)+ω(m,tk-1)
(2)
Zj(tk)=Hj(tk)X(tk)+vj(tk)
(3)
其中,m为模型标识,m=1,2,…,Nm,式(2)是模型m描述的被估计量的物理特性;j表示第j个传感器,j=1,2,…,Ns,式(3)是第j个传感器的测量方程;tk=kT,表示融合中心第k个融合周期的终止时间,tk-1则为第k个融合周期的起始时间;Φ(m,tk|tk-1)和Hj(tk)分别为模型m中被估计量从第k-1个融合周期到第k个融合周期的状态转移矩阵和传感器j在时刻tk的观测矩阵;ω(m,tk-1)和vj(tk)分别为模型m在时刻tk-1的系统噪声和传感器j在时刻tk的测量误差。{ω(m,tk)}和{vj(tk)}均为白噪声序列,且{ω(m,tk)}、{vj(tk)}和被估计量的初始状态X(0)互不相关。

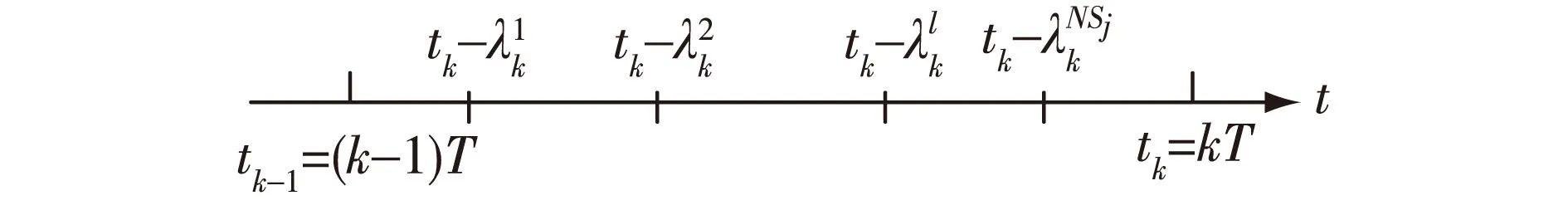
图1 单融合周期内目标i的量测时间分布

(4)
(5)
其中,
(6)
(7)
(8)
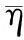
(9)
2.2基于交互多模型算法的异步信息融合估计
对于由单个传感器跟踪的目标,通过交互多模型算法对目标跟踪信息进行融合估计;对于由多个传感器构成的传感器组跟踪的目标,采用集中式处理方式,将等价伪量测的异步融合算法与IMM算法结合,实现对该目标的多个异步测量值进行融合估计。设跟踪某目标的传感器组由N个传感器组成,具体融合步骤如下。
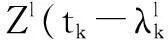
步骤2对第k-1个融合周期的状态估计信息X(m,tk-1|tk-1)、P(m,tk-1|tk-1)和μ(m,tk-1|tk-1)进行输入交互,其中m=1,2,…,Nm,求得各模型的预测概率μ(m,tk|tk-1)、模型的混合状态X0(m,tk-1|tk-1)和混合状态协方差P0(m,tk-1|tk-1);
步骤3以X0(m,tk-1|tk-1)和P0(m,tk-1|tk-1)为状态输入进行一步预测,得X(m,tk|tk-1)和P(m,tk|tk-1);
步骤4根据文献[6],目标在各模型下的异步测量信息的融合结果按式(10)和(11)计算:--------------------------------------------
(10)
(11)
(12)
步骤6根据各模型概率μ(m,tk|tk)、X(m,tk|tk)和P(m,tk|tk),计算第k个融合周期的总状态估计X(tk|tk)和P(tk|tk)。
2.3跟踪精度预测
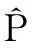
1)输入交互:根据第k-1个融合周期的状态估计信息X(m,tk-1|tk-1)、P(m,tk-1|tk-1)和μ(m,tk-1|tk-1)为输入,进行状态估计混合:
(13)
(14)
(15)
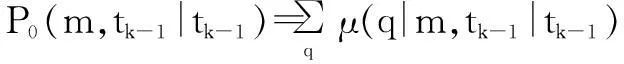
[X0(i,tk-1|tk-1)-X(q,tk-1|tk-1)]·[·]T}
(16)
2)结合Kalman滤波的思想,对状态混合信息进行一步预测:
X(m,tk|tk-1)=Φ(m,tk|tk-1)X0(m,tk-1|tk-1)
(17)
P(m,tk|tk-1)=Φ(m,tk|tk-1)P0(m,tk-1|tk-1)·
ΦT(m,tk|tk-1)+Q(m,tk-1)
(18)
(19)
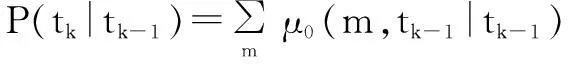
[X(tk|tk-1)-X(m,tk|tk-1)]·[·]T}
(20)
3)根据下式对N个测量时刻的测量值进行估计:
(21)
4)结合式(10)和(11)分别计算各模型的滤波误差协方差和状态预测值,再结合每个模型的预测概率对目标状态信息进行综合估计,各模型的状态预测值如式(22),目标状态的综合估计值如式(23)和(24):
(22)
(23)
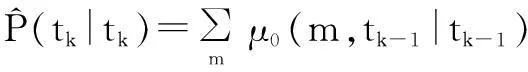
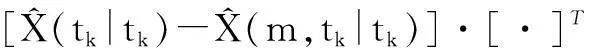
(24)
目标的跟踪需求通过计算各目标的预测协方差与期望协方差之间的差异确定。目前,用来度量矩阵差异性的常用方法有求两矩阵范数之差、两矩阵的行列式之差等[3]。本文选择矩阵的Frobonius范数(F-范数)之差作为衡量矩阵之间差异性的准则,则各目标的跟踪精度需求在分配算法执行的不同阶段可分别通过式(25)和(26)计算:
Req=f(P(tk|tk-1)-Pd(tk))
=||P(tk|tk-1)||F-||Pd(tk)||F
(25)

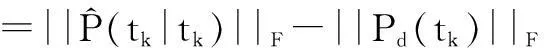
(26)
2.4基于蚁群算法的多传感器分配算法
根据蚁群算法的思想,所设计的求解多传感器多目标分配问题的优化模型的算法的具体步骤如下。

步骤2根据各传感器的任务状态,确定可用的传感器集合S(k);

步骤4设置蚂蚁数量NA,目标的重要程度ωi,迭代次数NI=0,最大迭代次数NImax,信息素τij,信息素启发因子α,信息素挥发系数ρ∈[0,1),期望启发因子β;
步骤5循环次数NI=NI+1;
步骤6随机生成S(k)中元素的一个排序,蚂蚁r按这一顺序依次游历各传感器;
(27)
(28)
τij=(1-ρ)τij+Δτij
(29)
(30)
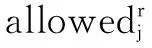
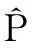
步骤10判断r是否将所有传感器游历完,若否,r继续游历,j++,返回步骤7;若是,记录r当前经过的路线对应的分配方案,判断在该方案中所有目标的期望跟踪精度是否都已得到满足,如果有目标没有达到期望跟踪精度,计算这一方案的目标函数值,与NA只蚂蚁搜索的局部最优方案比较,若优于局部最优方案,则替换,否则放弃r的方案;
步骤11r++,返回步骤6,当所有的蚂蚁完成各自的环游后,根据得到的局部最优方案,结合式(28)和(29)分别更新Δτij和τij,将所得局部最优方案与当前全局最优方案比较,若优于全局最优方案,则替换,否则放弃这一轮循环获得的局部最优方案;
步骤12若NI 步骤13根据所得方案,调度传感器集合对目标进行测量,并利用上文设计的基于交互多模型算法的异步信息融合估计方法,对各目标的测量值分别进行集中式融合,得到各目标在第k个周期的融合信息。 说明:步骤5至步骤12所描述的蚁群的搜索过程中,解决的是一个传感器跟踪一个目标的问题,对于一个传感器能同时跟踪N(N>1)个目标的问题,可假设将这类传感器分解成N个跟踪单目标的传感器,再采用步骤5至步骤12描述的方法解决这类问题。 3仿真分析 IMM算法的模型集由一个匀速(CV)运动模型、一个匀加速(CA)运动模型和一个匀速转弯(CT)运动模型组成,三个运动模型的系统噪声协方差均为I(I为单位矩阵)。目标在二维平面内运动,三个目标的相关参数及运动状态分别如表1和表2所示,四个传感器在二维平面内的距离误差和角度误差如表3所示。假设1号传感器不能测量2号目标,2号不能同时测量1号与3号目标,每个传感器能同时跟踪2个目标。融合周期和采样周期均为1s,各传感器的采样时刻离融合时刻的时间间隔分别为[0.8s,0.5s,0.3s,0.1s]。下面各表中,角度单位:度(∘),时间单位:秒(s),距离单位:米(m),速度单位:米/秒(m/s),加速度单位:米/秒2(m/s2)。 表1 目标初始参数 表2 目标运动状态 表3 传感器的测量误差 蚁群算法相关参数设置:NA=20,NImax=100,α=1,β=3,ρ=0.1,Q=100。 根据文中设计的多传感器管理方法,得到所假设的三个目标的跟踪轨迹如图2所示,图3和图4分别为图2中各融合周期目标轨迹的滤波值与真实值之间在x方向和y方向的均方根误差,表5是对应的各融合周期中传感器与目标之间的分配方案。 表4描述的是目标在每个融合周期结束时的跟踪需求,表5是对应的下一个融合周期中传感器与目标之间的分配方案,表4和表5中的第0个融合周期表示起始时刻,表5中,数字编号1,2和3分别表示三个目标,“-”表示在当前融合周期该行对应的传感器没有分配任务。从单个融合周期来看,文中设计的算法能根据同一周期内各目标的不同需求,动态地为目标分配传感器,以表4中t=10s为例,在第10个融合周期结束后,三个目标的跟踪需求之间的关系为:f2>f1>f3=0,在表5中,第11个融合周期,没有为目标3分配传感器,为目标1分配了传感器1,为目标2分配了传感器2和3;从整个融合过程来看,算法也能根据在不同阶段所有目标的需求变化,动态地调整各周期中传感器资源的占用情况,以节省传感器资源的开销,在前10个融合周期,随着对各目标的跟踪进入稳定状态,它们的跟踪需求也随之变小,表3中可以看出,传感器资源的使用量也随之减少,在10s~11s,目标2和3的运动状态发生变化,根据第10个融合周期完成时的跟踪需求为第11个周期分配的方案导致对目标2和3的跟踪精度急剧下降,在第11个融合周期结束时,这两个目标的跟踪需求大幅增大,因此在后续的融合周期中,目标2和3对传感器资源的占用量变大,随着对这两个目标的跟踪进入稳定状态,传感器资源的占用量也随之下降。 图2 目标跟踪轨迹 图3 目标x方向跟踪误差 图4 目标y方向跟踪误差 融合周期0123456789目标1559.16421.71110.8777.5445.172.18005.770目标2691.29184.64103.7570.6930.5919.944.71008.59目标3337.50209.2189.2708.7401.2303.290融合周期10111213141516171819目标10.5801.810.4704.1102.7100.11目标21118.3247.1930.4510.770.53006.220.210目标3698.9550.2464.734.1419.725.921.3903.490 表5 分配方案 4结束语 本文以多传感器协同跟踪地面目标为背景,根据协方差控制的思想,结合传感器自身、传感器与传感器之间、传感器与目标之间以及目标与目标之间的约束条件建立了多传感器多目标分配问题的优化模型。采用交互式多模型对地面机动目标的运动状态进行建模,引入基于伪量测的异步数据处理方法对多个传感器的异步观测数据进行融合,并推导了交互式多模型算法下用于估计各目标在每个融合周期的跟踪精度需求的异步传感器的信息增量的计算方法。最后依据蚁群算法的思想为这类多传感器多目标分配问题设计了求解算法,并通过仿真验证了算法的可行性。 参考文献: [1]王玉生,田康生,朱康,等. 基于目标估计协方差控制的传感器资源管理算法[J]. 现代防御技术, 2003, 31(2):52-54,64. [2]Kreucher C M, Hero A O, Kastella K D. A comparison of task driven and information driven sensor management for target tracking[C]∥Proc. of IEEE Conference on Decision and Control, and the European Control Conference, 2005:4004-4009. [3]王林,于雷,蔻英信,等. 以任务需求为驱动的多传感器资源管理方法[J]. 系统工程与电子技术, 2010, 32(9): 1925-1930. [4]杨啸天,冯金富,冯媛,等. 基于遗传粒子群的多传感器目标分配算法[J]. 电光与控制, 2011, 18(3):5-8. [5]吴巍,李朝霞,刘博,等. 基于多智能体与市场理论的多机载平台传感器管理[J]. 系统工程与电子技术, 2014, 36(1):68-75. [6]A. T. Alouani, T. R. Rice. On Asynchronous Data Fusion[C]∥Proc of the Annual Southeastern Symposium on System Theory, IEEE, 1994:143-146. [7]孙亚东,邢昌风,卢发兴. 一种多约束条件下的分布式多传感器协同规划算法[J]. 指挥控制与仿真, 2012, 34(6):31-35, 54. [8]辛玉林,徐世友,陈曾平. 基于最小代价和蚁群算法的传感器资源优化研究[J]. 信号处理, 2010, 26(1): 99-103. [9]王放,魏玺章,黎湘. 一种改进的多传感器多目标跟踪中的传感器管理方法[J]. 电光与控制, 2005, 12(2):11-13,18. [10]Blom H A P. An efficient filter for abruptly changing systems[C]∥Proc. of 23rd IEEE Conference on Decision and Control, 1984: 656-658. [11]Blom H A P, Bar-Shalom. The interacting multiple model algorithm for systems with Markovian switching coefficients[J]. IEEE Trans. On Automatic Control, 1988, 33(8):780-783. Multi-sensor Management Method Based on Tracking Accuracy Control LI Zi-fen, CHENG Jiang-tao, OUYANG Huan (Qingdao Campus of Naval Aeronautical Engineering Institute, Qingdao 266041, China) Abstract:The multi-sensor management problem is researched against the background of tracking ground maneuvering targets. Based on tracking accuracy control, a multi-sensor multi-target assignment method is proposed. Firstly, an optimization model is established which is based on covariance control and considers multi-restrictions on sensors and targets. Secondly, a method to estimate each target’s tracking accuracy at different data fusion periods is designed which combines the interacting multiple model algorithm and asynchronous fusion algorithm based on equivalent pseudo-measurements. At last, an algorithm for searching feasible assignment scheme for the multi-sensor multi-target assignment problem is designed according to the ant colony algorithm. The simulation results show that under ensuring tracking accuracy precondition, the management method can rationally allocate sensors for each target according to the importance of tracking task for each target. Key words:multi-sensor management; IMM; ground maneuvering target; asynchronous data fusion; ant colony algorithm 中图分类号:TN953;E911 文献标志码:A DOI:10.3969/j.issn.1673-3819.2016.02.009 作者简介:黎子芬(1982-),女,湖北天门人,博士,讲师,研究方向为航空火力控制技术。程江涛(1967-),女,硕士,副教授。欧阳寰(1970-),男,硕士,副教授。 收稿日期:2015-11-20 文章编号:1673-3819(2016)02-0037-06 修回日期: 2015-12-10