振荡式直线压缩机行程自传感算法研究

珠海格力电器机电技术研究院　张东盛　刘亚祥　程海珍　区均灌



振荡式直线压缩机行程自传感算法研究

珠海格力电器机电技术研究院张东盛刘亚祥程海珍区均灌

【摘要】通过理论分析和实验研究，分析了电机参数对无位置传感器计算结果的影响。实验结果表明：电阻对计算结果影响较小，基本可以忽略；电感对位移的相位影响较大，为保证谐振频率跟踪的准确性，需要对电感进行修正；反电势系数对位移的幅值有很大影响，需要进行修正和补偿。经过参数补偿后，位移自传感的计算精度可以达到3%以内，证实算法可行。

【关键词】无位置传感器；电阻；电感；反电势系数

0　引言

振荡式直线压缩机由于将提供运动动力的电机与压缩机做成一体，省去了将旋转运动转化为直线运动的中间转化机构，所以具有结构轻便，摩擦损耗小，可以直接通过控制活塞的行程实现变容量控制等多方面优点，但这种结构在带给我们便利的同时也存在一些缺点。这种结构的压缩机活塞运动时没有机械限位，很容易撞缸[1]。因此，为了实现变容量控制并防止撞缸，必须对动子的位移进行精确测量和控制，但从空间、成本和可靠性等各方面考虑，压缩机内部都不适合加装位移传感器，因此，为了实现压缩机小型、轻量、低成本，开发一套无位置传感器的动子位置检测算法是十分必要的[2]。

本文对振荡式直线压缩机电机运行原理进行了理论分析，并建立了模型。将无传感算法和有传感器得到的实验结果对比，验证了算法的可实施性。

1　直线压缩机位移自传感分析

振荡式直线压缩机主要是由机械弹簧共振系统与电磁系统的耦合作用下进行工作。由电压平衡方程式与力平衡方程式共同组成了动磁式直线压缩机的系统方程[3]。

电压平衡方程：

式(1)中：R—定子电阻；L—绕组电感；K0—电机的反电势系数；i—定子电流；U—电机端电压；X—动子位移。

电压平衡方程等效电路图如图1所示。

力平衡方程：

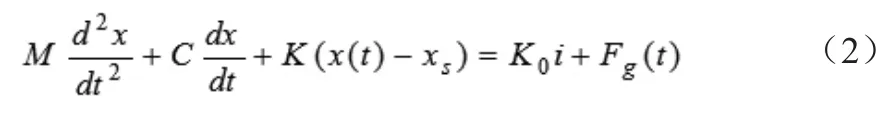
公式(2)中：M—动子质量，单位：kg；C—系统阻尼系数；K—弹簧刚度系数，单位：N/m；K0—电机的反电势系数；Fg—气体力；Xs—动子平衡位移；X—动子位移。

谐振系统受力图如图2所示。

图1　等效电路图

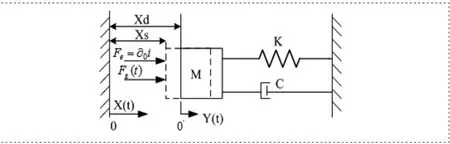
图2　谐振系统受力图

根据直线电机的电压平衡方程，可以得到位移的自传感计算公式为：

这种算法通过采集电机的端电压和电流信号，对动子的位移进行估算，再对位移的幅值进行检测，从而得到压缩机活塞运动的行程；计算中用到积分运算，实际编程中通常使用低通滤波替代纯积分运算，防止积分偏差[4]。

在公式(3)中，涉及到的电机参数有电阻R，电感L和反电势系数K0，下面我们分析这几个参数对行程估算精度的影响。

2　电机参数对自传感结果的影响

2.1电阻对无传感器行程估算的影响

在这几个电机参数中，电阻是最容易测量且准确度较高的变量，使用万用表就可以测出电阻的大小。根据实际调试经验，电阻对位移的相位影响很小，基本可以忽略，但对幅值有一定的影响，尤其是在压缩机负载情况下，电流较大时，电阻对幅值的影响更加明显[5]。电流越大，电阻的影响就越大。电阻越大，幅值越小。但结合实际情况来说，振荡式直线压缩机是低背压，吸气温度不高，电机定子温升低，电阻阻值变化范围比较小，因此可以用固定的电阻参数进行运算，误差在可接受范围内。

2.2电感对无传感器行程估算的影响

一般来说，电感与动子位移和电流大小有关，如图3所示，分别对比了直线压缩机在带载情况下7A电流和14A电流下，电感随位移变化的曲线。从图3可以看出，随着电流增大，电感会变小。

图3　电感参数随电流和位移变化曲线

由于电感参数一般较小，远小于1H，所以对计算结果的幅值影响较小，电感对无位置传感器计算结果的影响主要体现在相位上。我们以电流信号为参考，改变电感值，得到在不同电感值下电流与位移的相位差，表1中数据直线压缩机实际运行过程中改变电感值得出相位差的变化，从表中可以看出电感对相位的影响很大。我们知道，直线压缩机控制的一个要点是要保证其始终运行在谐振频率上，也就是要使电流与位移的相位差保持90°，在根据公式(3)进行位移估算时，电感对计算行程相位的影响也会对谐振频率跟踪控制产生影响。

表1　电感对相位的影响

从直线压缩机的力平衡方程公式(3)可以看出弹簧对动子所做的功为：

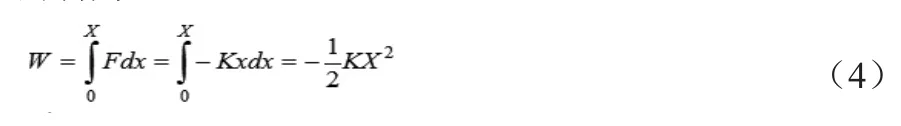
动子运动的动能可表示为：

当电机运行在共振频率时，电流与速度同相，电磁力与速度也是同相，那么电磁力始终做正功，弹簧做功转化为动子的动能[6]。

联合公式(4)(5)(6)，把压缩机电机动子的直线运动类比于一个圆周运动，则动子振幅，也就是计算的行程可以表示为：

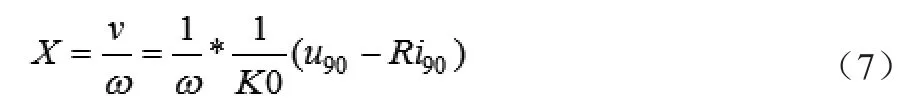
公式(7)只要测出电流相位为90°时的值和此刻对应的电压值就可以计算出直线压缩机的行程，消除电感对行程计算的影响[7]。但是公式(7)有个应用限制，就是只有压缩机运行在谐振频率才能准确计算出压缩机的行程，如果压缩机不是在谐振频率运行，电流相位滞后或者超前速度相位，此时计算出的压缩机行程会比实际行程小。

2.3反电势系数对无传感器行程估算的影响

在公式(3)和公式(7)中，反电势系数K0与位移x成反比关系，也就是说，反电势系数的大小对位移的相位没有任何影响，但会直接影响到位移幅值的大小。如图4所示是在固定反电势系数不变的情况下，压缩机实际运行情况下无传感计算行程与实际行程对比曲线图。

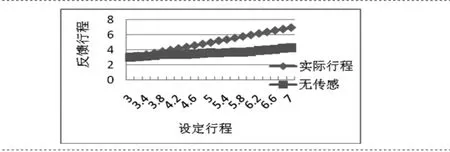
图4　固定反电势系数无传感计算结果

由图4可以看出，在压缩机行程增大的过程中，电机电流越来越大，磁路饱和，反电势系数越来越小，此时需要对反电势系数进行修正和补偿，否则行程计算误差越来越大。反电势系数与动子位置和电流有关，其变化曲线分别如图5和图6所示。

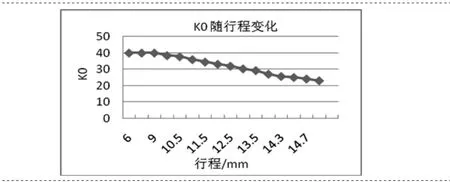
图5　反电势系数随行程变化曲线

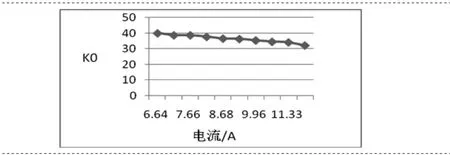
图6　反电势系数随电流变化曲线

由于我们采用的是行程控制，估算的行程本身就存在误差，因而根据行程来进行参数补偿误差较大。从电压方程可以看出，电流的变化也可以反映行程的变化，所以我们采用根据电流来进行反电势系数补偿[8]。从图中可以看出，K0随电流变化近似呈一条直线，在Matlab中对K0和电流进行拟合，再将拟合后的数据代入程序进行补偿，补偿后行程估算误差在3%以内，数据如表2所示。

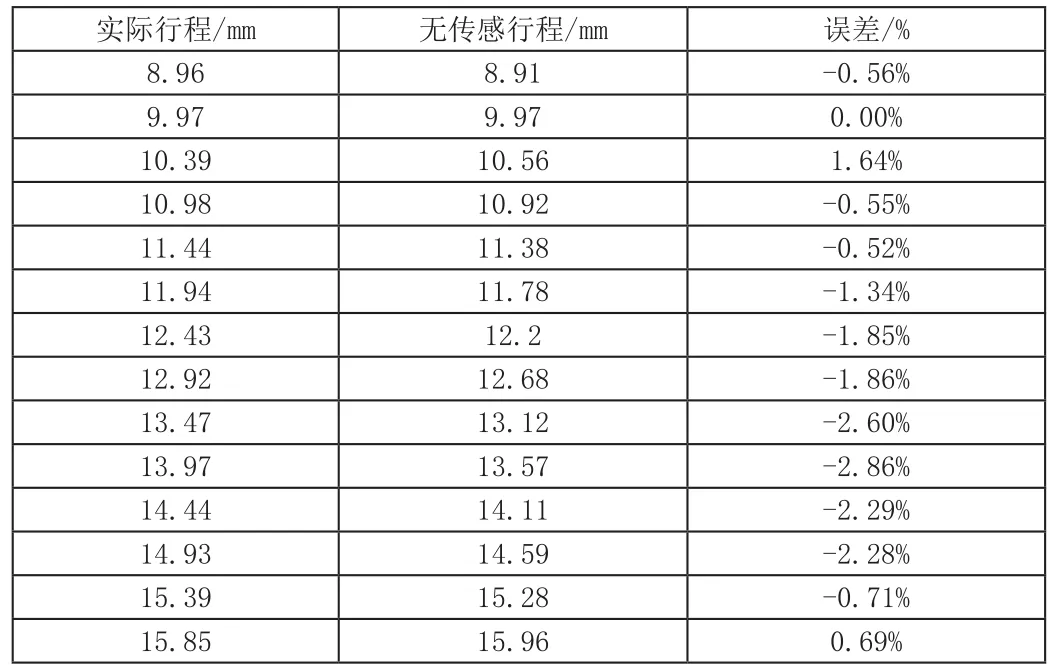
表2　无传感计算误差

3　补偿后的位移对比

在进行直线压缩机动子位置估算时，电阻对计算结果影响较小，电感在公式(3)对位移的相位影响较大，在公式(7)中对行程的计算没有影响，反电势系数对位移幅值有较大影响。为了保证无位置传感器计算结果的准确性，需要对电感和反电势系数进行修正和补偿，如图7所示是经过补偿后的无传感位移和传感器采集的位移对比，说明适当地对参数进行修正可以保证计算结果的准确性。

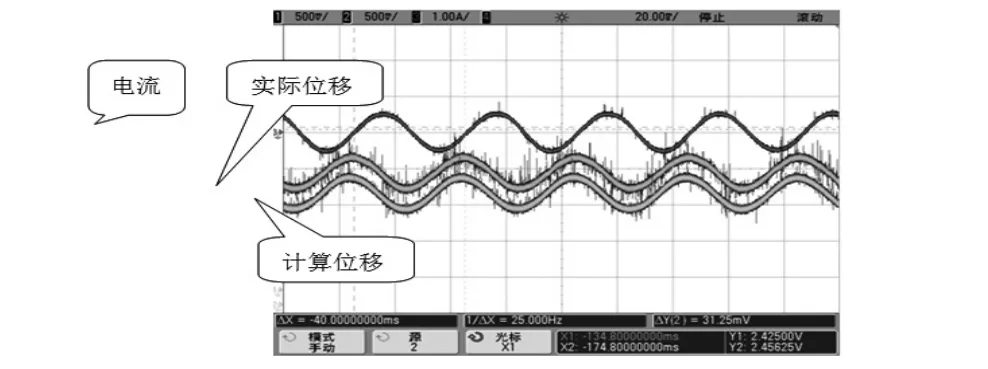
图7　无传感与传感器位移对比

图7中上面紫色的波形为电流波形，中间黄色的波形为实际位移波形，下面绿色的波形为计算位移波形。

4　结论

本文在对振荡式直线压缩机电机运行原理理论分析的基础上，建立了直线压缩机的模型。将无传感算法和有传感器得到的结果对比，实验结果表明：以忽略电阻对计算结果的影响；为保证谐振频率跟踪的准确性，需要对电感进行修正；反电势系数对位移的幅值有很大影响，需要进行修正和补偿。经过参数补偿后，位移自传感算法的计算精度可以达到3%以内，验证了算法的可实施性。

参考文献

[1]陈梁远,李黎川.压缩机用直线电机及其关键技术发展综述[J].中国电机工程学报,2013,33(15):52-61．

[2]Ji Won Sung,Chel Woong Lee,Gyu-Sik Kim,T.A.Lipo,Chung-Yuen Won and Sewan Choi.Sensorless control for linear compressor[J].International Journal of Applied Electromagnetics and Machanicc.2006,24(4):273-286.

[3]直线电机原理与应用[M].北京:机械工业出版社,2000.

[4]于明湖,张玉秋,叶云岳,等.双定子直线振荡电机动子位移自传感技术研究[J].传感技术学报,2010,23(6):803-807．

[5]Zhu Yu-wu,Cho Yun-yun.Thrust Ripples Suppression of Permanent Magnet Linear Synchronous Motor[J].IEEE Trans.On Magnetics,2007,43(6):2537-2538．

[6]张金权,畅云峰,牛元君,等.直线冰箱压缩机活塞位移的自传感器技术研究[J].西安交通大学学报,2007,41(9):1049-1053.

[7]熊超,王龙一,郑文鹏,等.两种动磁式直线振荡电动机功率损耗分析[J].微特电机,2012,40(3):27-33．

[8]赵鹏,李志海,郑水英,等.直线压缩机余隙行程综合流量调节法[J].浙江大学学报(工学版),2012,46(3):509-514.

张东盛（1976—），男，广东珠海人，工程师，主要从事变频压缩机，伺服电机的驱动研究。

Research on Stroke Self-sensing Algorithm of Linear Oscillatory Compressor

ZHANG Dong-sheng，LIU Ya-xiang，CHENG Hai-zhen，OU Jun-guan (Gree Electric Appliances Inc，Zhuhai 519070，China)

Abstract：The effect of linear motor parameters on senseless displacement calculation was carried out by means of experiment and study. The results show that the impact caused by resistance is so little that can be ignored.The inductance produces an effect on the phase of senseless displacement.For the exactness of resonance frequency following，it’s necessary to correct the inductance.The back electromotive force(BEMF) coefficient produces an effect on the amplitude of displacement.It’s also necessary to correct the BEMF coefficient.After these correction，the error of self-sensored displacement can be less than 3% ,the feasibility of algorithm is testified.

Key words：sensorless；resistance；inductance；BEMF coefficient

作者简介：