钢包底吹氩均混时间及临界流量水模型实验
2016-05-02刘中秋李林敏曹茂雪李宝宽
刘中秋,李林敏,曹茂雪,李宝宽
(1. 东北大学冶金学院,沈阳110819;2. 武汉科技大学耐火材料与冶金国家重点实验室,武汉430081)
钢包底吹氩均混时间及临界流量水模型实验
刘中秋1,2,李林敏1,曹茂雪1,李宝宽1
(1. 东北大学冶金学院,沈阳110819;2. 武汉科技大学耐火材料与冶金国家重点实验室,武汉430081)
针对钢包底吹氩工艺,通过改变透气砖数量、单透气砖吹气位置、双透气砖夹角、喷吹气体流量、渣厚等参数,对钢包的均混时间进行了水模型实验研究.提出临界流量的概念,发现吹气量超过临界流量后均混时间明显减小.结果表明:单透气砖喷吹时,相同吹气量下偏心喷吹时的均混时间比中心喷吹时短,临界流量小;双透气砖喷吹时,透气砖夹角越大,均混时间越短,临界流量越小.
钢包;均混时间;临界流量;水模型实验
炉外精炼是指在特定的包括真空和各种气氛条件下进行脱氧、脱硫、去除杂质、调整成分、夹杂物变性、控制和均匀钢水温度等的冶金过程.随着冶金技术的发展,对钢冶炼中温度和成分的控制精度要求越来越高,炉外精炼技术已成为高品质钢生产过程中必不可少的冶金工艺之一.

本文采用水模型实验对钢包底吹氩工艺过程进行研究,提出“临界流量”的概念.揭示了吹气位置、透气砖个数和渣厚对临界流量的影响规律.
1 实验原理及方法
进行底吹钢包水模型实验要保证几何相似和动力相似.本实验模型与原型(40 t钢包)的几何相似比λ取值为 1∶3,建立底吹钢包的物理模型,原型及模型尺寸见表1.引起底吹钢包系统内部流动的主要作用力为气泡的浮力,实验中通过保证模型与原型的Froude(Fr)数相等来满足动力学相似.目前主要有三种保证动力相似的气体流量转换方法.方法1:利用式(1)进行转换,这是最早出现的研究方法,但是经过不断地研究发现,该方法的准确性较低.方法2:利用修正的Frm数式(2)转换,与方法1相比,这种方法的准确性有了很大提高,是当前普遍采用的方法.方法3[13]:利用无量纲数G进行转换,它是最新得到的流量转换方法,其来源是对修正的Frm数进行了再次修正.该方法的最大特点是采用气泡羽状区形成时的速度作为特征速度,利用这一转换方法得到的实验数据与前人结果吻合较好.
(1)
(2)
(3)
式中,U为气体特征速度;g为重力加速度;L为特征长度;ρg为气体密度;ρl为液体密度;U0=Q/A0为初始气体速度,Q为体积流量,A0为透气砖进气口面积;H为熔池深度.
本文采用无量纲数G满足动力相似,模型(m)与原型(p)的气体流量换算关系可以由气相无量纲数相等得到,即Gm=Gp,整理可得:
(4)

由于实际炼钢过程中,气体进入钢包前存在一定的压力变化,且进入钢包后由于温度升高,使得气体体积迅速增大.由标准状况到钢包充气口的变化过程为升温升压的过程,可由下式进行描述:
(5)
式中,Tp、T0分别为钢水温度和室温;QAr为标准状况下氩气气体流量;P0、Pp分别为标准大气压下和钢包充气口压力,其中Pp=P0+ρstgh.
最后获得水模型与原型之间的气体流量关系为:
QN2=0.011QAr
(6)
得到水模型流量与原型实际流量关系见表2.
采用透明有机玻璃和钢结构支架做主体材料,建立钢包水模型实验系统.整个系统包括钢包、钢结构底座、多孔透气砖、储气瓶、电导率仪、计算机等.其中钢结构底座可以实现单透气砖偏心距调节和双透气砖夹角的调节.实验系统如图1所示.
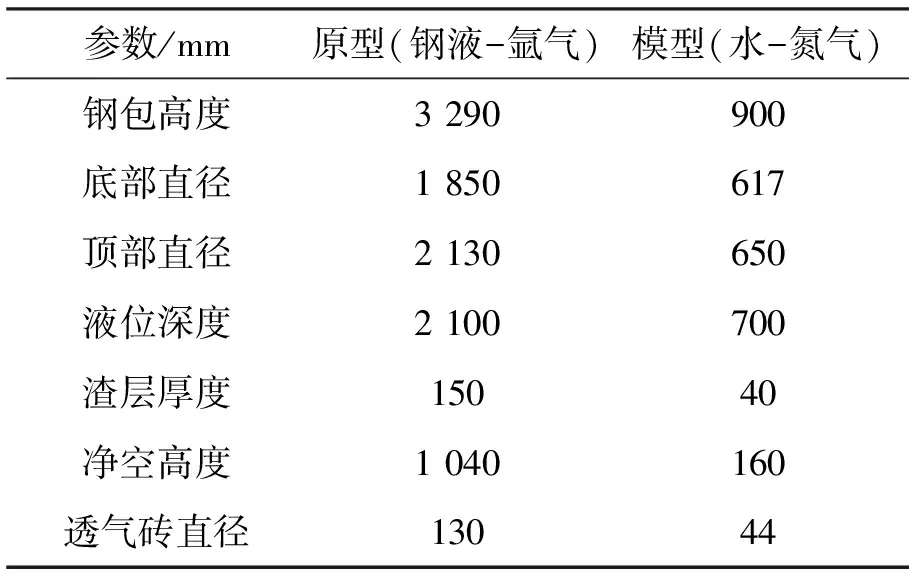
表1 钢包结构参数

表2 水模型流量与原型实际流量
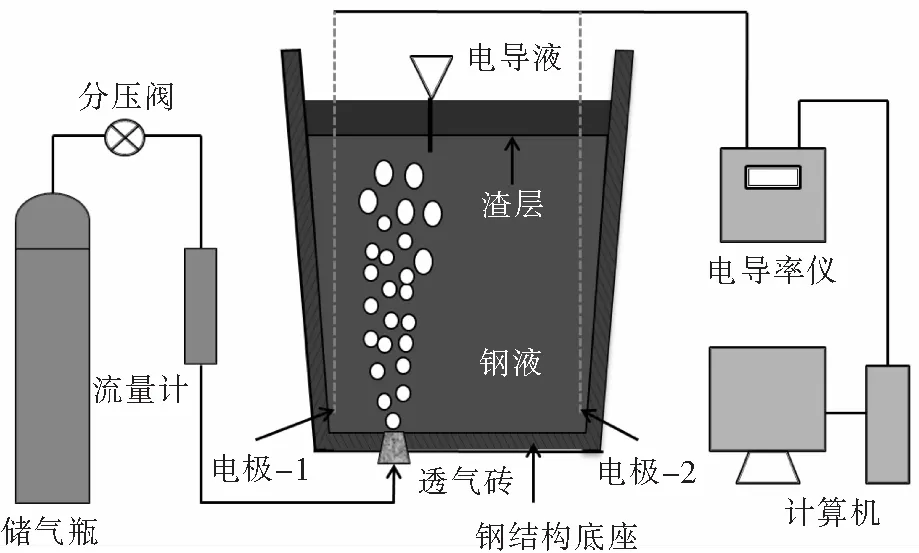
图1 实验系统示意图
2 均混时间实验
现行的底吹钢包模型实验中,对均混时间的测量都是通过测量溶液电导率或者pH值变化来间接得到均混时间的数值.本文采用间接的“刺激—响应法”来测量均混时间.选取两个最难混合的位置进行测量,两个电极探头沿模型底部透气砖所在直径放置,深入模型底部,并靠近壁面.其中离透气砖较近的测量点称为近测点(测点1);反之,称为远测点(测点2),如图2所示.

图2 均混时间电极测点位置

图3 单透气砖实验均混时间测量结果
实验中为确保所得均混时间的准确性,每次实验连续进行五次测量,并取平均值.图3所示为单透气砖不同位置所得的均混时间大小.由图可知,随着吹气量的增加,均混时间呈现减小的趋势,但中心喷吹时(0R)流动不稳定,均混时间波动性较大.对比不同吹气位置的结果发现,相同吹气量下,偏心喷吹时(0.67R)的均混时间更短.对比远、近两个测点的数据显示,远测点2的均混时间要小于近测点1的结果.根据钢包均混时间原理,以混匀最慢的点作为钢包的均混时间.因此,选取距离透气砖较近的测量点(测点1)所得结果作为单透气砖喷吹时的均混时间.

图4 双透气砖实验均混时间测量结果
对于双透气砖钢包而言,不同透气砖夹角时,喷吹气体在钢包内所形成的流动有一定差异,当夹角很小时,两股气流相互碰撞可能会消耗掉部分能量,影响流动速度;而夹角增大时,可以避免或减小气流的冲撞作用.这表明透气砖夹角对均混时间的影响不可忽略.图4所示为双透气砖不同夹角所得的均混时间大小.图中显示,不论喷吹夹角多大,随着流量的增大,均混时间都呈现出减小趋势.这说明在一定范围内增大气体流量可以提高钢包的搅拌效率,减小均混时间.对比不同夹角的数据发现,透气砖夹角为180°时的均混时间要短于夹角为60°时的均混时间,即均混时间随着透气砖夹角的增大有减小趋势.虽然双透气砖喷吹夹角有所不同,但是平均值的变化趋势都显示出近测点1要略大于远测点2所得均混时间.因此,仍将近测点1所得均混时间作为双透气砖钢包的均混时间.
3 临界流量
在钢包底吹工艺中,吹气可以实现多个目的.例如:促进钢水温度及成分均匀,排除钢包内部夹杂物,促进脱硫、脱碳、脱磷等反应的进行等.要达到这些目的需要采用不同的流量,低流量主要用来均匀温度及成分、排除夹杂物;高流量主要用来促进脱硫和脱碳等反应的进行.因此,需要找到一个临界流量去界定低流量和高流量,从而实现钢包的精确控制,提高钢包效率.
在实际生产过程中很难通过钢液的变化去衡量临界流量,但是钢包顶部渣层的存在为选取临界流量提供了条件.低流量时主要为了均匀温度及成分、排除夹杂物,则不应让渣眼持续存在,因为渣眼的存在会消耗很大的能量,且会引起卷渣.因此,可以通过渣眼的变化去衡量临界流量.当某一吹气条件下,渣眼处于“时开时合”状态,即气体流量不能完全支持渣眼的存在,称这一吹气流量为“临界流量”.高于临界流量时,渣眼将持续存在;低于临界流量时,渣眼基本不存在.临界流量下渣眼的变化形态如图5所示.

图5 临界流量下渣眼的变化形态
图6给出了单透气砖实验下吹气流量对均混时间的影响.对于不同偏心距下的喷吹实验,临界流量均在60 L/h附近.结果发现,小于临界流量时,均混时间减小趋势较平缓;当流量超过临界流量时,均混时间先是急剧下降,之后减小趋势变得平缓.对于均混时间由急剧下降变为相对平缓的阶段,主要原因为流量较小(大于临界流量)时,部分能量开始作用于渣眼,但是初始阶段这部分能量占总能量的比重较小,所以呈现出一段均混时间急剧下降的过程,流量继续增大时,维持渣眼形态所耗费的能量占总能量比重增大,搅拌作用减弱,使得均混时间下降趋势变平缓.
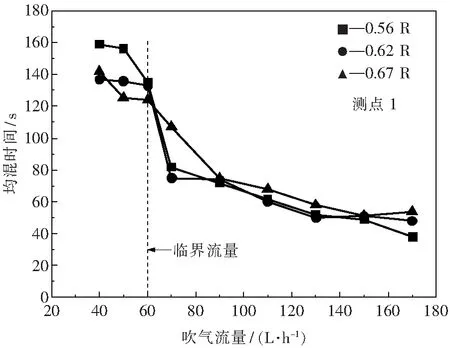
图6 吹气流量对均混时间的影响

图7 单透气砖不同位置及渣厚下的临界流量

图8 双透气砖不同夹角及渣厚下的临界流量
在单透气砖喷吹实验过程中,研究了 0 R、0.5 R及0.67 R三个不同位置和20、30、40及 50 mm 四个不同渣厚下的临界流量.所得不同位置和渣厚的临界流量结果见图7.由图可知,临界流量与渣厚成正比,且渣厚越大时,临界流量增大幅度越明显.因为渣厚增大时,吹动渣层所需要的能量就随之增大.从吹气位置来看,相同渣厚下中心喷吹时(0 R)所需临界流量大于偏心喷吹,且吹气位置越靠外,临界流量越小,即临界流量 0.67 R<0.5 R<0 R .中心喷吹时,气体对渣层的作用面积较大,这就需要更多的能量去搅动渣层;而偏心喷吹时,由于靠近壁面使得气体对渣层的作用面积相对较小,其所需能量较中心喷吹小,使得偏心喷吹时的临界流量略小于中心喷吹.
图8示出了双透气砖实验条件下的临界流量测量结果.结果发现,随着渣厚的增大,不论透气砖夹角多大,其临界流量都呈现增大趋势.且渣厚由 20 mm 增加到 30 mm 时,不同夹角的临界流量整体差距增大;而渣厚继续增加时,这一差距又有一定的减小.在相同渣厚条件下,随着透气砖夹角的增大,临界流量逐渐减小.实验过程中发现,当夹角较小时,两股气流会有部分的冲撞,而这一冲撞可能会导致气体的能量降低,所以需要更大的流量去吹动渣层,使得临界流量增大;而夹角足够大时,两股气流无法冲撞,所以临界流量相对较小.
4 结 论
(1)对于底吹钢包均混时间的测量,应选取距离透气砖较近的测量点(测点1)所得结果作为底吹钢包的均混时间.
(2)不论单透气砖还是双透气砖吹气,均混时间都随着吹气流量的增大而减小.小于临界流量时,均混时间减小趋势较平缓;当流量超过临界流量时,均混时间先是急剧下降,之后减小趋势变得平缓.
(3)单透气砖喷吹时,相同吹气量下偏心喷吹时(0.67R)的均混时间比中心喷吹时短;且中心喷吹时流动不稳定,均混时间波动较大.
(4)双透气砖喷吹时,夹角为180°时,其均混时间相对较短;夹角为60°时,两股气柱相互影响,使得均混时间较长.
(5)单透气砖喷吹时,吹气位置越靠近壁面,临界流量越小;双透气砖喷吹时,透气砖夹角越大,临界流量越小.
[1]Mazumdar D, Guthrie R. Mixing models for gas stirred metallurgical reactors[J]. Metallurgical and Materials Transactions B, 1986, 17(4):725-733.
[2]Joo S, Guthrie R. Modeling flows and mixing in steelmaking ladles designed for single- and dual-plug bubbling operations[J]. Metallurgical and Materials Transactions B, 1992, 23(6):765-778.
[3]Francisco D, Marco A. Effect of both radial position and number of porous plugs on chemical and thermal mixing in an industrial ladle involving two phase flow[J]. ISIJ International, 2011, 51(7):1110-1118.
[4]Adrian M, Marco A, Conejo A. Effect of slag properties on mixing phenomena in gas-stirred ladles by physical modeling[J]. ISIJ International, 2014, 54(1): 1-8.
[5]Nakanishi K, Fujii T, Szekely J. Possible relationship between energy dissipation and agitation in steel processing operations[J]. Ironmaking and steelmaking, 1975, 2(3):193-197.
[6]Haida O, Emi T, Yamada S. Injection of lime base powder mixture to desulfurize hot metal in torpedo cars[C]//2nd International Conference on Injection Metallurgy Organized by MEFOS and JERKONTORET[C]. Lulea Sweden, 1980, 20:1-20.
[7]Qu Y, Liu Y, Liu L. 2nd International conference on injection metallurgy organized by MEFOS and JERKONTORET[C]. Lulea Sweden, 1980, 20: 21.
[8]Conejo A , Kitamura S, Maruoka N, Kim S. Effects of top layer, nozzle arrangement, and gas flow ration mixing time in agitated ladles by bottom gas injection [J]. Metallurgical and Materials Transactions B, 2013, 44(4):914-923.
[9]Mazumdar D, Guthrie R. Modeling energy dissipation in slag-covered steel baths in steelmaking ladles[J]. Metallurgical and Materials Transactions B, 2010, 41(5): 976-989.
[10]Li B K, Yin H B, Zhou C Q,etal. Modeling of three-phase flows and behavior of slag/steel interface in an argon gas stirred ladle[J]. ISIJ International, 2008, 48(12): 1704-1711.
[11]Lou W T, Zhu M Y. Numerical simulation of gas and liquid two-phase flow in gas-stirred systems based on Euler-Euler approach[J]. Metallurgical and Materials Transactions B, 2013, 44(5): 1251-1263.
[12]Li L M, Liu Z Q, Li B K,etal. Water model and CFD-PBM coupled model of gas-liquid-slag three-phase flow in ladle metallurgy[J]. ISIJ International, 2015, 55(7): 1337-1346.
[13]Krishnapisharody K, Irons G. A critical review of the modified Froude number in ladle metallurgy[J]. Metallurgical and Materials Transactions B, 2013, 44(6):1486-1498.
Water model of mixing time and critical flow rate in a gas-stirred ladle
Liu Zhongqiu1,2, Li Linmin1, Cao Maoxue1, Li Baokuan1
(1. School of Metallurgy, Northeastern University, Shenyang 110819, China;2. The State Key Laboratory of Refractories and Metallurgy, Wuhan University of Science and Technology, Wuhan, 430081, China)
In view of the ladle bottom argon blowing process, the mixing time was studied by changing the number of nozzles, position of single nozzle, angle between double nozzles, gas flow rate and thickness of slag layer in a water model experiment. A concept of critical gas flow was proposed. It was found that the mixing time decreases obviously when the gas flow rate is above the critical one. The result showed that when a single nozzle is used, the mixing time with the gas eccentric injection is shorter than with the gas center injection under the same gas flow rate, and the critical flow rate is smaller. When the double nozzles were used, the mixing time is shorter while the angle between nozzles increases and the critical flow rate is smaller.
ladle; mixing time; critical flow rate; water model experiment
10.14186/j.cnki.1671-6620.2016.03.004
TF 777
A
1671-6620(2016)03-0176-05
