数学文化视角下的中考试题赏析及其思考

摘要：数学文化在上个世纪80年代后就受到国内外数学家和数学教育家的高度关注，数学史、数学审美、数学的精神和思想方法等构成数学文化的内涵。让数学史料、审美、名题、游戏、故事等文化元素走进中考，亲近数学、品味数学和欣赏数学的魅力，突显数学的价值，激发学生对后继数学学习的兴趣和热情，促进一线老师对数学文化的重视，都有着十分重要的作用。值得思考的是，部分省市的命题专家在数学文化渗透中考试题时，没有引起足够的重视，认为数学文化的试题仅仅是装饰一份试卷的美观而已，没有体现数学文化理性思维本质内涵，编制数学文化试题缺乏创新。数学文化的试题要注重与数学“四基”的有机结合，要突出理性思维的本质内涵。特别地要对教材中的例题、定理、习题和阅读材料等方面进行深层次的挖掘、重构。

关键词：数学文化；中考试题；欣赏；思考建议；命制策略

中图分类号：G633.6 文献标识码：A 文章编号：1009-010X（2016）06-0061-05

一、数学文化

数学文化是人类文化的重要组成部分，上个世纪80年代后就受到国内外数学家和数学教育家的高度关注.为此，2001年《数学课程标准（实验稿）》倡导：“教材中要注重体现数学的文化价值，在对数学内容的学习过程中，教材可以在适当的地方插入介绍有关数学发现与数学史的知识，丰富学生对数学发展的整体认识，…”。与此同时，十年后的《数学课程标准（2011版）》又重申：“数学文化作为教材的组成部分，应渗透在整套教材中。为此，教材可以适时地介绍有关背景知识，包括数学在自然与社会中的应用，以及数学发展史的有关材料，帮助学生了解在人类文明发展中数学的作用，激发学习数学的兴趣，感受数学家治学的严谨，欣赏数学的优美。…”。在这一理念的指导下，各种版本的数学教材在每章节中都安排“阅读材料”，这些阅读材料蕴含丰富的数学文化价值。那么，什么是数学文化呢？数学文化的概念至今还没有确切的定义，国内学者从不同的侧面给出数学文化相关的解读。徐乃楠，王宪昌认为：“数学文化是数学史、数学与文化学、社会学的交叉学科。”黄秦安认为：“数学文化是超越（扩大并包含）数学科学范围的数学观念、意识、心理、历史事件，人物和数学传播的总和。”顾沛认为：“数学文化简单地说指数学的思想、精神、方法、观点、以及它们的形成和发展；广泛些说，除上述内涵外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等。”宋乃庆等认为“数学及与数学产生相互作用的各种文化对象，包括哲学、历史、政治、教育、艺术、经济、思维科学及各门自然科学，构成一个动态系统。这个动态系统即数学文化。其相互作用的方式是双向的和交叉的，一方面数学以其内在的力量推动文化的进步，另一方面数学从相关文化中汲取动力和养分。”比较上述学者对数学文化的理解，数学文化的主要内涵是数学家在解决问题和探索的过程中，所形成的数学史、数学审美、数学精神及其数学的应用等。

二、中考试题中的数学文化赏析

作为初中最后一个环节的数学中考试题中，如何体现渗透数学文化这一理念呢？如何把文化理念从务虚走向务实呢？近年来擞学文化走进各省市中考试题，数学命题专家在初中最后一次考试评价中，不忘数学情感教育的渗透，把数学的育人价值、数学的理性精神、数学的神奇美蕴含在考试中，让学生亲近数学、品味数学和欣赏数学的魅力，展现数学文化的价值，激发学生对后继数学学习的兴趣和热情，促进一线老师对数学文化的重视，都有着十分重要的作用。纵观2015年全国中考试题，数学文化融人试题表现在以下几个方面。

（一）数学史料中的文化元素

题1：（2015年北京市中考试题）《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架。它的代数成就主要包括开方术、正负术和方程术。其中，方程术是《九章算术》最高的数学成就。《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两。问牛、羊各直金几何？”译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两。问每头牛、每只羊各值金多少两”？设每头牛值金x两，每只羊各值金v两，可列方程组为

。

题2：（2015甘肃省武威市中考试题）古希腊数

学

家

把

数1，3，6，10，15，21，…叫做三角形数，其中1是第一个三角形数，3是第2个三角形数，6是第3个三角形数，…依此类推，那么第9个三角形数是__，2016是第__个三角形数。

赏析：由于数学的历史发展过程中蕴含着丰富的数学文化素材，不同民族、不同文化背景下生长着不同类型的、不同水平和不同范式的数学文化。中国古代受实用主义思想的影响，数学的发展沿着经世致用的观念展开，中国古代最重要的数学经典著作《九章算术》，它就是一本与现实生活密切相关的数学问题集。题1一方面介绍了该书在中国古代数学史上重要的地位和价值，另一方面让学生了解该书在代数学上研究的内容，通过具体的题目让学生列出方程，这样设计的试题，符合学生的认知水平，又结合具体问题，对中国古代传统数学的认同感。相反，在西方文明的源头古希腊，他们认为：“上帝是一位几何学家，按照数学的方式去设计世界。”如古希腊数学家毕达哥拉斯提出了“万物皆数”，他认为“数”是世界万物背后的规定性，并为抽象的“数”提供“形”的解析，是第一次为数插上了形的翅膀，该学派不仅研究三角形数、四边形数、五边形数等，而且还研究其它的数，如完美数、亲和数等。题2可以根据形的特点去寻求数的规律，也可以根据数列的特点归纳数列的一般规律，用数形结合的思想探寻规律，题目叙述简洁、形式熟悉亲切，内含丰富。以数学史为背景，很好地考查了学生对数学知识的理解，提高了对数学的认识。

（二）数学审美中的文化元素

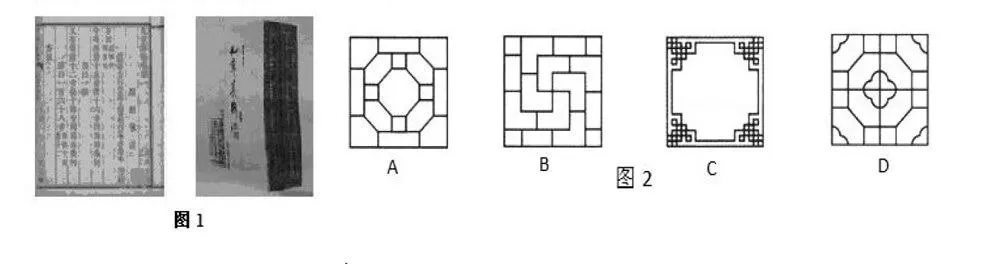
题3：（2015山西中考试题）晋商大院的许多窗格图案蕴含着对称之关，现从中选取以下四种窗格图案，其中是中心对称图形但不是轴对称图形的是（

）

题4：（2015年重庆市中考试题）如果把一个自然数各数位上数字从最高位到个位依次排出一串数字，与从个位到最高位依次排出的一串数字完全相同，那么我们把这样的自然数叫做“和谐数”.例如：自然数64746从最高位到个位排出的一串数字是：6、4、7、4、6，从个位到最高排出的一串数字也是：6、4、7、4、6，所以64746是“和谐数”。再如：33，181，212，4664，…，都是“和谐数”。

（1）请你直接写出3个四位“和谐数”，猜想任意一个四位“和谐数”能否被11整除，并说明理由；

（2）已知一个能被11整除的三位“和谐数”，设个位上的数字为x（1≤x≤4，x为自然数），十位上的数字为y，求y与x的函数关系式。

赏析：题3挖掘山西省有地方特色的晋商大院窗格图案，这些图案形式上对称、和谐、简洁，给人带来美丽、漂亮的感受。做题的过程是享受美、发现数学之美的过程，这些古代窗格图案既有轴对称图形，也有中心对称图形，在审美过程中确认概念的内涵和外延。

张奠宙先生认为数学美育价值有4个层次：美观、美好、美妙、完美。上述题3给学生以美观和美好之感的前两个层次，那么题4却是对美观和美好的超越，从形的对称之美过渡到数，自然数也存在对称之美，并定义这样一类自然数为“和谐数”，以开放的视角对“和谐数”展开探究，试题的设计沿着感受“和谐数”的美观和美好，然后追寻她的美妙，品味探索“美妙”的心境，从而激发学生对数学的热爱。总之，数学的审美是超越功利性的，中考试题挖掘美的元素，激发学生的审美情感和审美追求，陶冶学生的情操，中考试题融人数学之美，让学生少一份对数学的憎恨，多一份对数学的好感，对还原数学本真的一面起到了积极的作用。

（三）数学游戏中的文化元素

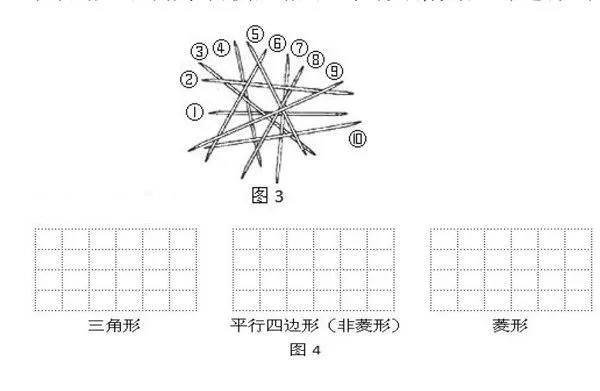
题5：（2015年浙江义乌数学中考试题）挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走。如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走

A.②号棒 B.⑦号棒

C.⑧号棒 D.⑩号棒

题6：（2015山东青岛中考试题）小颖和小丽做“摸球”游戏：在一个不透明的袋子中装有编号为1-4的四个球（除编号外都相同），从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字。若两次数字之和大于5，则小颖胜，否则小丽胜。这个游戏对双方公平吗？请说明理由。

赏析：国际著名数学大师陈省身临终前不久曾为少年数学爱好者题词：“数学好玩”。题5以孩子们常见的挑游戏棒为背景走进中考，让考生重温孩儿时挑游戏棒惊心动魄而又充满紧张的心理状态。这一切不是通过具体实物操作，而是通过学生仔细地观察和空间想象完成这一心理实验，试题以游戏的形式很好地考查学生的空间观念和几何直观，也体会到数学是一门有趣而好玩的学科。题6是以“摸球”游戏来确认规则是否公平，重在考查学生求等可能性事件常用的方法。美国著名科普作家马丁·加德纳曾经对数学游戏的教育价值作了如下相当正确的评价：“唤醒学生的最好办法是向他们提供有吸引力的数学游戏、智力题、魔术、笑话、悖论、打油诗或那些呆板的教师认为无意义而避开的其它东西。”数学游戏却以娱乐大众的面目出现在中考最后一个环节中，令人耳目一新，考查数学基础知识变得生动有趣。引发了学生对数学的兴趣，数学是好玩的。改善中考试题枯燥乏味性，比纯粹为考试而考试更有价值。

（四）数学名题中的文化元素

题7：（2015年湖南常德中考试题）取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1。这个结论在数学上还没有得到证明。但举例验证都是正确的。例如：取自然数5。最少经过下面5步运算可得1，如果自然数m最少经过7步运算可得到1，则所有符合条件的m的值为__。

题8：（2015宁波中考试题）如图4，在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形。记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S=ma+nb-1，其中m，n为常数。

（1）在下面的方格纸中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；

（2）利用（1）中的格点多边形确定m，n的值。

赏析：题7来源于“角谷猜想”，洛萨·科拉茨是德国数学家，他在1937年提出了一个著名的猜想：任给一个正整数n，如果n是偶数，就将它减半（即n/2）；如果n是奇数，则将它乘3加1（即3n+1），不断重复这样的运算，经过有限步后，一定可以得到1。后来一位名叫角谷的日本人把它带到亚洲，因而人们就顺势把它叫做“角谷猜想”。题8是奥地利数学家皮克发现一个计算点阵中多边形面积的公式：S=a+0.5b-1。这两题都是对历史上的数学的名题作适当的介绍和改编，让考生重新经历数学曾经火热的思考过程，品味思维的愉悦，享受数学探索的乐趣。正如波利亚所说：“在一个易受外界影响的年龄阶段，这样的经历可能会培养出对智力思考的爱好，并对思想和性格留下终生的影响……，他们在尝到数学带来的乐趣以后，他就不会轻易地忘记，于是数学就有机会成为他生活的一部分：一种爱好，或者他专业工作中的一种工具，或者他的职业，或者是一种崇高的抱负。”中考试题让学生解决数学问题类似于数学家研究过程，让他们经历那种既紧张又喜悦思维，让考生终身难忘。

（五）故事和会标中的文化元素

题9：（2015年四川乐山）电影《刘三姐》中秀才和刘三姐对歌的场面十分精彩。罗秀才唱到：“三百条狗交给你，一少三多四下分，不要双数要单数，看你怎样分得均？”刘三姐示意舟妹来答，舟妹唱道：“九十九条打猎去，九十九条看羊来，九十九条守门口，剩下三条财主请来当奴才.”若用数学方法解决罗秀才提出的问题，设“一少”的狗有x条，“三多”的狗有v条，则解此问题所列关系式正确的是（ ）

题10：（2015年浙江嘉兴中考试题）下列四个图分别是四届国际数学家大会的会标：

其中属于中心对称图形的有

A.1个 B.2个 C.3个 D.4个

赏析：题9是以电影《刘三姐》中秀才和刘三姐的精彩对话为背景，刘三姐机智解决秀才的问题，突显了三姐的聪慧，给考生以新颖而有趣的感觉。题10是以国际数学家大会的会标为主题设计试题，第一个图案是第24届国际数学大会会标，取材于中国古代数学家赵爽的勾股圆方图；第二个图案是第18届在芬兰举行的国际数学大会会标，会标的图案为“膜结构”的部分几何图形；第三个图案是第27届在韩国举行的国际数学大会会标，会标的图案是阿基米德螺线；第四个图案是第21届在日本举行的国际数学大会会标，会标用几何图形构建大和民族传统文化元素。国际数学家大会的会标美轮美奂，每一个会标的图形蕴含的数学意义丰厚。数学的试题取材经典的影片，不仅给考生以趣味，而且让学生觉得数学无处不在；取材国际数学大会会标开阔学生的视野，让学生心系数学的发展，为中考试题增添了一道亮丽的风景。

三、数学文化融入中考试题的思考及建议

数学文化讲述数学的发展历程，讲述数学的思想和方法，讲述数学的价值与作用，讲述数学家发现创造数学的心路历程，体会再创造的快乐。数学文化能让人从宏观上把握数学，掌握一种思想，开阔思维，创新方法。中考试题中融人数学文化，可以改变一线老师对数学文化仅是花边式、点缀式的看法，更加重视课堂数学文化的融入，重视教材中“阅读材料”的挖掘和开发；学生受数学文化的熏陶和影响，数学的视角不再狭窄，数学给人的感觉不再等同于做题，数学慢慢突显出更广阔的景色，生动、活泼可爱的一面被更多学生所接受。这正是数学文化文而化之的结果，春风化雨、润物细无声的作用。

值得注意的是，部分省市的命题专家在数学文化渗透中考试题时，没有引起足够的重视，认为数学文化的试题仅仅是装饰一份试卷的美观而已，没有体现数学文化理性思维本质内涵，编制数学文化试题缺乏创新，老是在勾股定理上重复打圈，没有对数学文化试题进行大胆地尝试。当然部分省市的中考试题，如2015年山西省中考试题等，把数学文化和数学的知识有效地整合，在数学文化试题命制方面进行大胆地创新。纵观2015年全国中考数学文化试题，有的通过直接识记，考查学生数学课外阅读面；有的直接通过数学史上的问题、书本上的问题解决方法或定理证明方法；有的对历史上数学名题进行改编；有的是通过创设情境，体现数学应用价值；有的融游戏、电影等于数学试题中；试题给人清新亮丽之感。当然我们反对为文化而文化的试题，数学文化的试题要注重与数学“四基”的有机结合，要突出理性思维的本质内涵；要对教材中的例题、定理、习题和阅读材料等方面进行深层次的挖掘、重构；特别是阅读材料蕴含丰富的数学文化，要对其进行深层次的整合。例如，人教版八（下）教材中的二次根式一章中有阅读材料“海伦一秦九韶三角形面积公式”，可以采取以下策略命制：

命制策略一：对这两个公式之间的等价性进行命制，能否由秦九韶的公式推导出海伦公式？考查学生的代数式恒等变换能力。

命制策略二：对海伦——秦九韶公式的推广，考查学生推理、数学活动经验、思想方法等综合能力。

（1）三角形中的海伦公式是否可以任意推广到四边形，若不能，举出反例。

（2）请探索在什么条件下的四边形，它的面积仅与四条边的长度有关？它又能满足

（3）若∠B+∠D=180°，上述四边形面积公式是否成立？若成立，请证明，若不成立，请说明理由？

命制策略三：新定义：“三边长为整数，且它的面积也为整数的三角形为海伦三角形。”考查学生在新情境下数学的综合运用能力。从特殊到一般，判断特殊的直角三角形，三边长分别为3、4、5，是否海伦三角形？然后控制变量，在格纸上画一个海伦三角形，最后放在新的情景中，如平面直角坐标进行运用，具体拙文。

命制策略四：也可以查找数学家海伦写的《测度术》一书中相关数学问题，编制数学问题，具体见文编制的问题。

总之，数学文化中考试题既要突出数学基础知识和基本技能的考查，又要突显数学文化的整体育人的要求，凸显理性思维的本质内涵。

[责任编辑 姜华]