地震勘探中的三维随机介质模拟及其特点分析

杨帆

（中石化华北油气分公司采油一厂，甘肃庆阳　745000）



地震勘探中的三维随机介质模拟及其特点分析

杨帆

（中石化华北油气分公司采油一厂，甘肃庆阳745000）

摘要：常规的均匀层状介质理论已经不适用于高分辨率地震勘探，需要进一步发展随机介质理论，为研究复杂非均匀介质中的地震波场理论奠定基础。本文首先利用三维Von Karman型自相关函数模拟三维随机介质并给出了详细的建模流程，通过引入三维锥形函数，来压制建模时离散计算产生的误差，提高了模型的可信度。然后详细讨论了自相关长度、谱指数、标准差对建立的三维随机介质模型的影响。最后分析了模型内的速度变化和概率分布情况。模拟结果表明利用三维Von Karman型自相关函数可以更灵活地模拟三维随机介质。

关键词：三维随机介质；三维Von Karman型自相关函数；自相关长度；谱指数

在地震勘探中，长期以来都是以传统的均匀介质或层状均匀介质理论为基础，从而忽略了实际地震勘探中介质的局部非均匀性，但是随着高分辨率地震勘探的不断发展、勘探目标已由常规油气藏逐渐转向复杂油气藏，介质中分布的大量微小异常会影响勘探结果[1]。用传统的介质模型理论很难准确地描述这些异常，而以统计学理论为基础的随机介质模型可以较为灵活、方便、有效地描述这些介质的微小异常，从而便于研究局部非均匀介质的地震波场的变化特征[2-4]。

国内外很多学者对随机介质理论已经进行了大量理论研究，并取得了一些成果。Ikelle等建立了二维随机介质模型并进行了正演模拟[5-7]。国内自2001年至今，姚姚等在这方面做出了很多成果，他们给出了随机介质模型的建立方法、并对各种随机介质模型进行了波动方程正演模拟以及波场特征分析等方面进行了深入的研究[8-19]。本文利用三维Von Karman型自相关函数建立了三维随机介质模型，引入三维锥形函数来压制离散误差，并对自相关长度、谱指数、方差三个模型参数对三维随机介质模拟的结果和特点分别进行了详细讨论，并对模型内的速度和概率分布情况进行了分析，来验证模型的可行性。

1　三维随机介质的建模原理及步骤

1.1随机介质的建模原理

随机介质模型可由大尺度和小尺度的非均匀的两部分所组成，大尺度部分描述介质的平均特性，即传统意义上的地质模型；小尺度部分是加在地质模型上的随机扰动，通常使用一个均值为零的、平稳的空间随机过程来表示。以三维弹性随机介质为例。各向同性的弹性介质由其密度ρ和拉梅系数λ、μ所确定。介质中相应的纵、横波速度分别为：

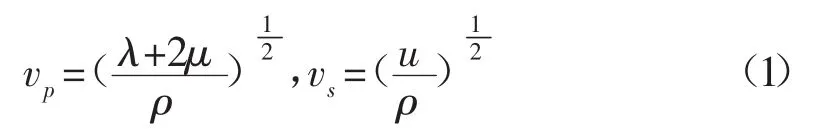
在随机介质中，空间坐标点（x，y，z）处的介质参数λ、μ和ρ可分别由下式表示为：

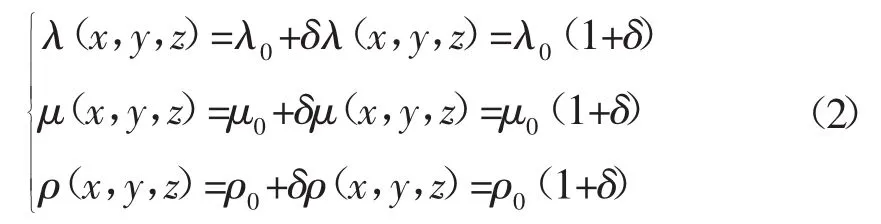
其中，λ0、μ0、ρ0为大尺度非均匀介质参数，即背景参数，可假设其为常数或随空间坐标（x，y，z）缓慢变化；δλ、δμ、δρ为小尺度非均匀扰动量，即随机扰动。根据（1）式可知，弹性介质可由其密度ρ和其中的纵波、横波速度vp、vs所确定。根据Brich[20]原理，可用纵波速度的相对扰动量来描述随机介质在小尺度上的非均匀性：

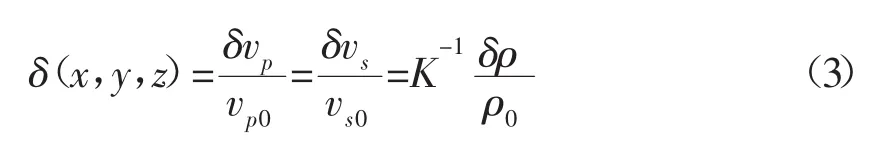
其中，vp0、vs0、ρ0为背景参数；K为比例常数，取值范围为0.3～0.8。假设δ＝δ（x，y，z）是均值为零且具有一定自相关函数及方差的空间平稳随机过程，由（3）式得：

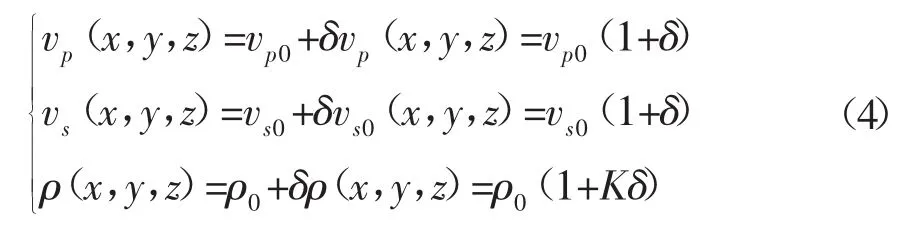
1.2随机介质的构建步骤

构建平稳随机过程的步骤如下：（1）选择自相关函数。如今的自相关函数有高斯型、指数型、Von Karman型、混合型及一些改进型的自相关函数，它们分别具有不同的特点，适应不同的地质情况。本文采用Von Karman型相关函数，它描述的随机介质具有多尺度、自相似的特点，其表达式为：

其中，K0为修正函数，a、b、c分别为介质在x，y，z方向上的自相关长度。

（2）产生随机过程功率谱。将（5）式作三维傅里叶变换得：

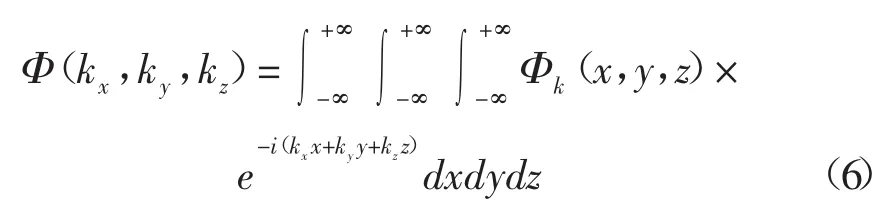
由（6）式得随机过程功率谱，其表达式为：

其中，kx，ky，kz分别为介质在空间域x，y，z对应波数域上的波数，ax、ay、az分别为横向、纵向、垂向上的谱指数。

（3）产生三维随机场。用随机数发生器生成［0，2π］区间上服从均匀分布的独立的三维随机场θ（kx，ky，kz）。

（4）计算随机功率谱。由下式可得随机功率谱：

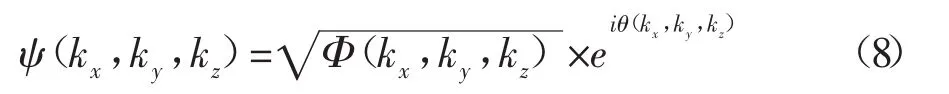
（5）计算ψ（kx，ky，kz）的三维傅里叶逆变换，由下式可得到逆变换Φk（x，y，z）：

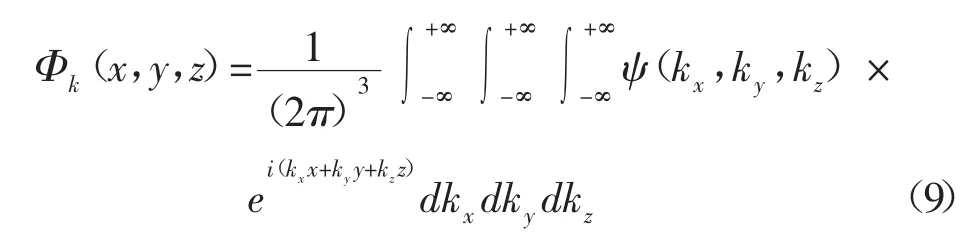
（6）计算Φk（x，y，z）的均值及方差：

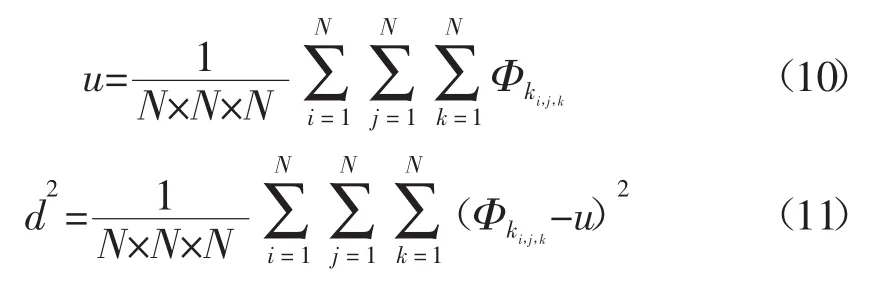
（7）通过规范化产生均值为零、方差为ε2，并以Φk（x，y，z）为自相关函数的二阶平稳随机过程：

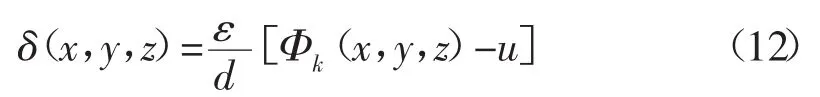
（8）结合（4）式和（14）式可得随机介质模型的速度函数，从而建立随机介质模型：

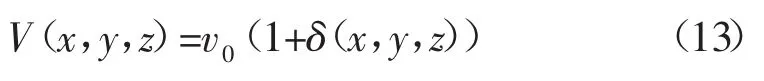
其中：v0-背景速度。

2　随机介质模型的误差压制

由于在离散数据的计算过程中会产生误差，使得随机函数不满足假设条件，因此在计算随机功率谱时，引入三维锥形函数来消除这种误差[18]，如下式：

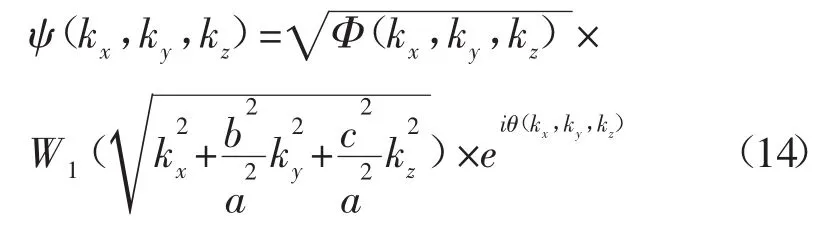
其中W1是一维情况下的锥形函数，其表达式为：

其中kzmax为锥形函数的半径（Marple[21]）。

图1　三维锥形函数示意图

建立了大小为250×250×250个网格（步长为1 m）的三维锥形函数（见图1），锥形函数的半径为0.5 m-1，从图1中可以看出，锥形函数的作用是压制随机模型中的低波数分量。

3　三维随机介质的建立及特点分析

为了便于对比分析，在引入三维锥形函数的前提下，假设各模型网格大小250×250×250（步长为1 m），背景速度v0=3 500 m/s，模型的其他特点通过改变标准差、谱指数、自相关长度来控制。

3.1固定标准差、谱指数，研究自相关长度对模型的影响

固定模型参量：标准差ε=0.1，谱指数长度ax＝ay＝az=2，改变自相关长度a、b、c和可以产生不同的三维随机介质模型，详情（见图2）。图2a和2b的自相关长度均相等，模拟的是各向同性时的三维随机介质模型。由图2a和2b可以看出，自相关长度越大，模拟的三维随机介质模型的尺度越大。图2c和2d的自相关长度不同，增大某一方向的自相关长度，则该方向速度趋向于一致，随机模型的层状特点逐渐明显，通过增加1个或2个方向的自相关长度到无穷大可以模拟各种各向均匀的薄互层状随机介质[18]。

3.2固定标准差、自相关长度，研究谱指数对模型的影响

固定模型参量：标准差ε=0.1，自相关长度a=b=c= 1 m，改变谱指数ax，ay，az，可以产生不同的三维随机介质模型，详情（见图3）。图3a和3b同样模拟的是各向同性时的三维随机介质模型，由图3a和3b可以看出，谱指数的大小对应着随机介质尺度的大小，并且谱指数越大，所得到的随机介质模型越光滑。图3c和3d表明，通过增加1个或2个方向的谱指数到无穷大同样可以模拟各种各向均匀的薄互层状随机介质。

3.3固定谱指数、自相关长度，研究标准差对模型的影响

固定模型参量：自相关长度a=b=c=1 m，谱指数ax=ay=az=2，引入三维锥形函数，改变标准差，可以产生不同的三维随机介质模型，详情（见图4）。从图4中可以看出，其他参数不变的情况下，改变标准差，从所得的三维随机介质模型几乎看不出区别，但是从旁边的色标值可以看出，标准差越小，其速度扰动越小，即标准差不同，得到的随机扰动的范围就不同，从而可以反映出实际介质的非均质性。

图2　改变自相关长度时建立的三维随机介质模型

图3　改变谱指数时建立的三维随机介质模型

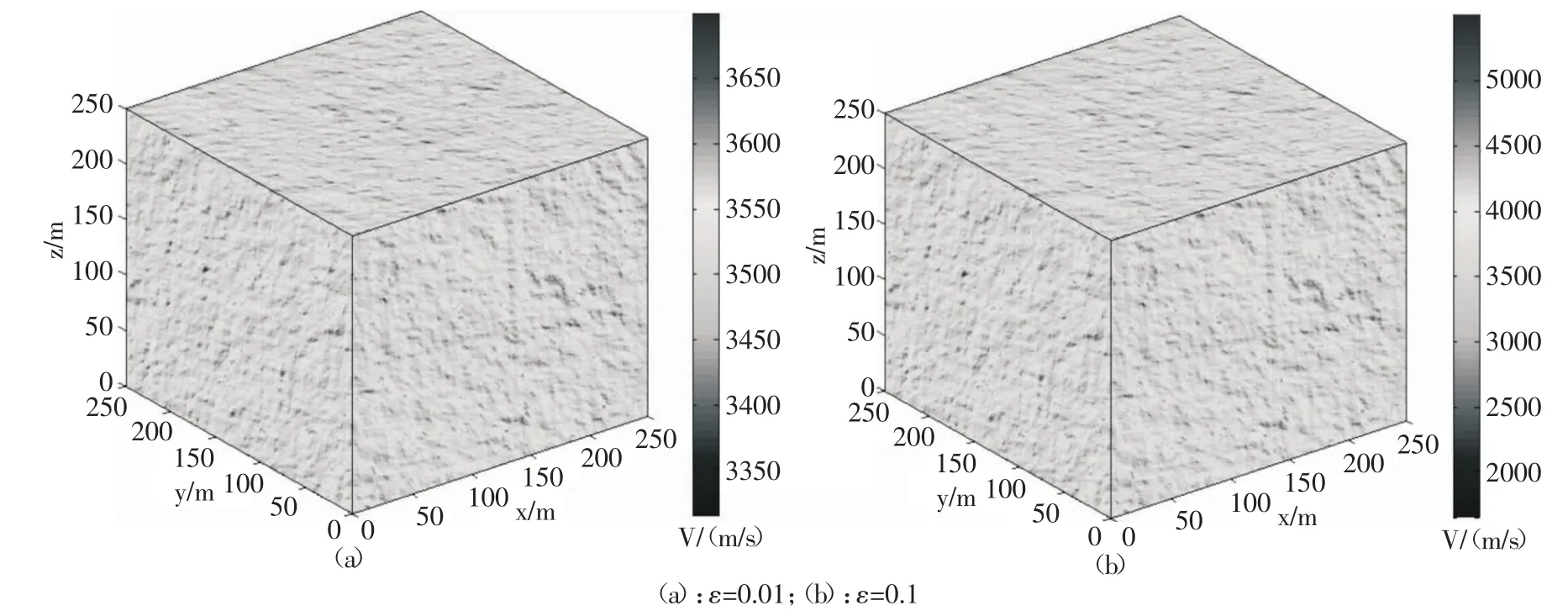
图4　改变标准差时建立的三维随机介质模型

4　随机介质模型中的速度变化及概率分布

从上面所建立的模型图中可以非常清晰地看到随机介质模型的特点，改变自相关长度、谱指数和标准差，可以得到不同的介质模型，但是无法了解模型内的速度变化和概率分布情况。从图2a中所建立的模型的x、y、z方向上随机抽取一维数据体，详情（见图5）。另外统计出各个速度概率分布，速度变化区间为500 m/s，详情（见图6）。

从图5和图6中可以得到，模型内的速度值在x、y、z方向上都是在背景速度v0=3 500 m/s上下浮动，与随机介质的基本假设比较吻合，即随机扰动的均值为零，但扰动的范围与标准差有关。从图6中可以看出，模型内的速度在x、y、z方向上呈正态分布，与相差越小，速度分布样本数越多，概率越大。统计结果表明，随机介质模型内的速度大多分布在1倍标准差范围内，其概率大约为75 %，2倍标准差范围内的速度概率大约为15 %。因此可知，随机介质模型内的速度符合统计规律，说明所建立的模型具有可行性。

5　结论

在前人的基础上，给出了三维Von Karman型自相关函数模拟随机介质的详细流程。在建模过程中，通过引入三维锥形函数，减小了随机建模时离散数据的计算误差。为了讨论自相关长度、谱指数等参数对模拟随机介质时的影响，通过改变这些参数来模拟三维随机介质模型，可知每种参数对模型结果的影响不同。从模拟的图可以看出，运用Von Karman型自相关函数模拟的三维随机介质模型与实际的地下岩芯图十分相似，通过改变各种参数(自相关长度、谱指数、标准差等)，能够灵活地描述多种实际介质在小尺度上的非均匀性的特点。随机介质模型理论为进一步研究实际三维地质体中小尺度的非均质性对地震波传播特征的影响打下了一定的基础。

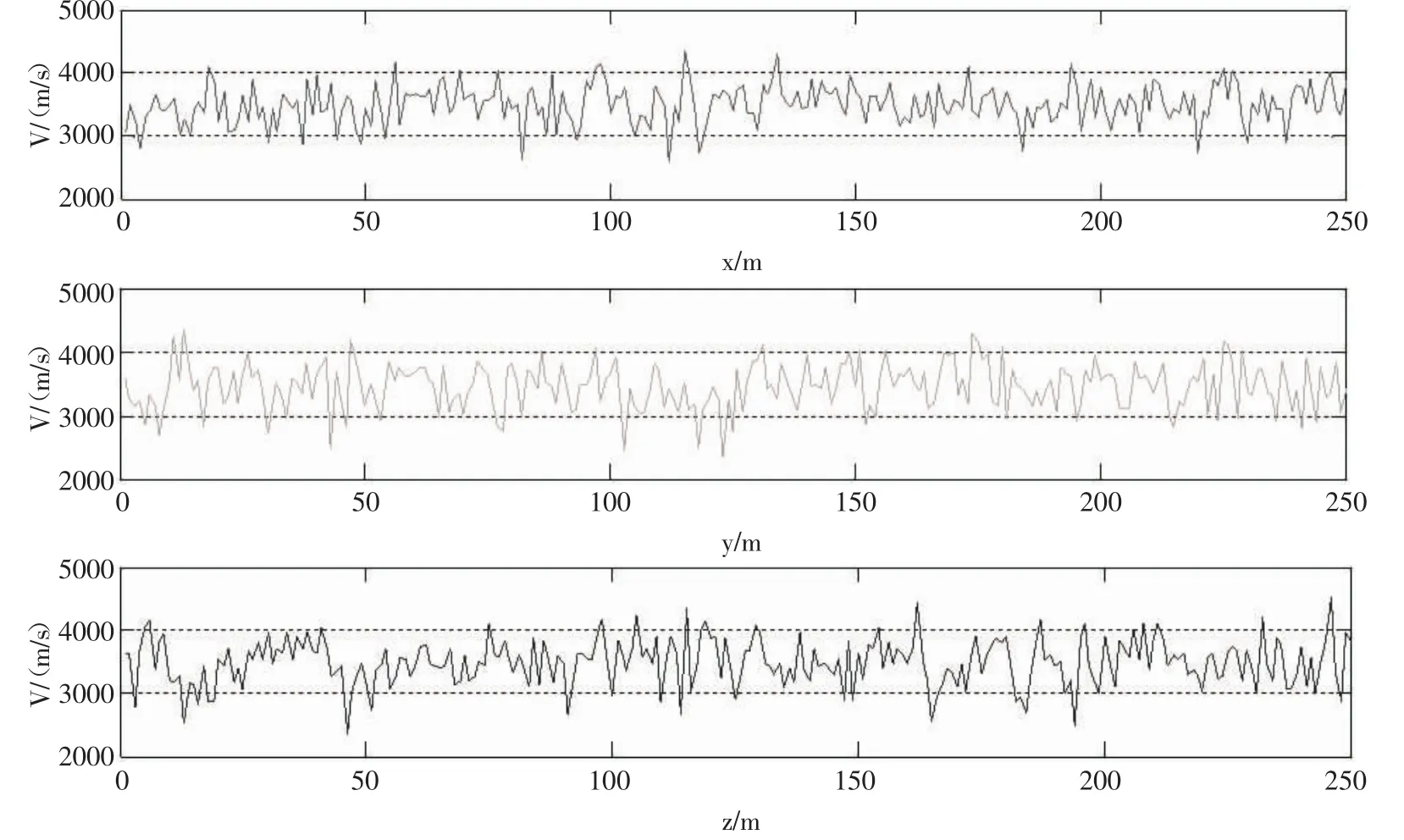
图5　随机介质模型在x、y、z方向上的速度变化

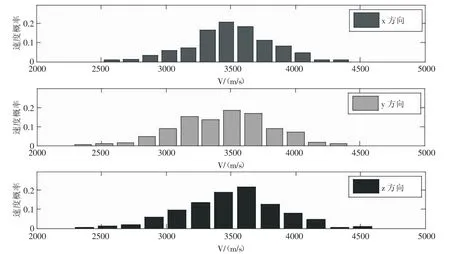
图6　随机介质模型在x、y、z方向上的速度概率分布

参考文献：

［1］李灿苹，王南萍，李志宏.Von Karman型自相关函数模拟随机介质［J］.物探与化探，2010，34（1）：98-102.

［2］李灿苹，刘学伟，李敏锋，等.非均匀地质体散射波特征初探［J］.石油物探，2006，45（1）：134-140.

［3］何又雄，姚姚.分形方法在模拟非均匀介质模型中的应用［J］.石油物探，2005，44（3）：199-201.

［4］何又雄，姚姚.各向异性分形介质模拟［J］.江汉石油学院学报，2004，26（4）：67-69.

［5］Ikelle L.，Yung S.，Daube F.2 -D random media with ellipsoidal autocorrelation functions［J］.Geophysics，1993，58 （9）：1359-1372.

［6］Korn M.，Seismic wave in random media［M］．1993：247-269.

［7］Engintav S.，Canitez N.，Modeling of multi -scale media in discrete form［M］．1997: 77-96.

［8］奚先，姚姚.二维弹性随机介质中的波场特征［J］.石油地球物理勘探，2004，20（1）：679-685.

［9］奚先，姚姚.二维随机介质及波动方程正演模拟［J］.石油地球物理勘探，2001，36（5）：546-552.

［10］奚先，姚姚.非平稳随机介质模型［J］.石油地球物理勘探，2005，40（1）：71-75.

［11］姚姚，奚先.区域多尺度随机介质模型及其波场分析［J］.石油物探，2004，43（1）：1-7.

［12］奚先，姚姚.随机介质模型的模拟与混合型随机介质［J］.地球科学，2002，27（1）：67-71.

［13］吴何珍，符力耘，兰晓雯.基于随机介质模型的储层非均质性分析［J］.地球物理学进展，2008，23（3）：793-799.

［14］陈可洋.三维随机建模方法及其波场模拟分析［J］.勘探地球物理进展，2009，32（5）：315-320.

［15］王金山，陈可洋，吴清岭，等.随机介质模型的一种构造方法［J］.物探与化探，2010，34（2）：191-194.

［16］刘春园，朱生旺，魏修成，等.随机介质地震波正演模拟在碳酸盐岩储层预测中的应用［J］.石油物探，2010，49（2）：133-139.

［17］殷学鑫，刘洋.二维随机介质模型正演模拟及其波场分析［J］.石油地球物理勘探，2011，46（6）：862-872.

［18］郭乃川，王尚旭，郭锐，等.地震勘探中三维小尺度非均匀性随机介质模型的建立及其特点分析［J］.石油天然气学报，2012，34（7）：62-67.

［19］徐振旺，安勇，支玲，等.运用分形方法模拟地震勘探中的三维随机介质［J］.地球物理学进展，2014，29（3）：1319-1325.

［20］Brich F.The velocity of compressional waves in rocks to 10 kilobars -Part 2［J］.Journal of Geophysical Research，1961，66（7）：2199－2224.

［21］Marple S.L.，Digital spectral analysis with application［M］.New Jersey，1987．

Simulations and characteristics analysis of 3-D random medium in seismic prospecting

YANG Fan
（The First Exploitation Factory of Huabei Oil & Gas Filed Company，SINOPEC，Qingyang Gansu 745000，China）

Abstract:The conventional layered medium seismic wave field theory has been unable to fit the high- resolution seismic exploration, we need further develop random medium theory in order to lay the foundation for the study of complex seismic wave-field theory in heterogeneous medium.This paper firstly gives the detailed process of 3-D Von Karman type autocorrelation function to simulate 3-D random medium and introduces 3-D cone-shape function to surpress discrete calculation errors of modeling and improve the credibility of the model, and then discusses the impact of autocorrelation length, spectral exponent and standard deviation on 3-D random medium.Finally, we analyze the velocity change and the probability distribution of model.The results show the method of that simulating 3-D random medium with Von Karman autocorrelation function is more flexible.

Key words：3-D random medium；3-D Von Karman type autocorrelation function；autocorrelation length；spectrum exponent

作者简介：杨帆，男（1989-），硕士，2013年毕业于中国地质大学（北京）地质工程专业，从事石油地质工作，邮箱：786495972@qq.com。

*收稿日期：2015－12-08

DOI:10.3969/j.issn.1673-5285.2016.02.018

中图分类号：TE132.14

文献标识码：A

文章编号：1673-5285（2016）02-0072-06