基于博弈论的频谱动态管理研究
2016-04-28郑臻哲
吴 帆 郑臻哲
(上海交通大学电子信息与电气工程学院 上海 200240)
(fwu@cs.sjtu.edu.cn)
基于博弈论的频谱动态管理研究
吴帆郑臻哲
(上海交通大学电子信息与电气工程学院上海200240)
(fwu@cs.sjtu.edu.cn)
Game Theory Based Spectrum Dynamic Management
Wu Fan and Zheng Zhenzhe
(SchoolofElectronic,InformationandElectricalEngineering,ShanghaiJiaoTongUniversity,Shanghai200240)
AbstractWith the growing deployment of wireless communication technologies, radio spectrum is becoming a scarce resource. The current static spectrum management leads to low spectrum utilization in the spatial and temporal dimensions. Auction mechanism is believed to be an effective method among the most effective tools to solve or relieve the problem of radio spectrum shortage. However, designing a practical spectrum auction mechanism has to consider five major challenges: strategic behaviors of rational users, channel heterogeneity, channel spatial reusability, preference diversity and social welfare maximization. In this paper, we give a though literature survey about spectrum auction mechanism design, and point out the disadvantage of the existing works. We also present our recent work in heterogeneous spectrum management. We model the problem of heterogeneous spectrum allocation as a combinatorial auction. By jointly considering the five design challenges, we propose an efficient channel allocation mechanism and a price calculation scheme. We also prove that the proposed mechanism satisfies the strategy-proofness, and achieves approximately efficient social welfare.
Key wordswireless network; channel allocation; combinatorial auction; game theory; resource management
摘要随着无线通信技术的快速发展,无线频谱成为越来越紧缺的网络资源.现有的静态频谱管理机制导致频谱资源在空间维度和时间维度上的低利用率.拍卖机制被认为是解决频谱资源稀缺问题的行之有效的方法.然而,设计高效、实际的频谱拍卖机制需要考虑5个挑战:理性用户自私策略行为、信道异质特性、信道空间重用特性、用户偏好多样性和社会福利的最大化.对频谱拍卖机制的研究现状做了全面的综述,指出现有工作存在的问题,并提出可行的解决方案;展示了在异质频谱管理中的最新研究成果;将异质频谱的重分配问题建模成组合拍卖模型,结合5个设计难题提出高效的信道分配机制和定价策略.该机制实现了防策略性和近似社会福利最大化.
关键词无线网络;信道分配;组合拍卖;博弈论;资源管理
过去的20年见证了无线网络和移动通信技术的快速发展,然而有限的频谱资源成为越来越多的无线应用和服务的发展瓶颈.频谱动态分配是移动互联网的基础技术之一.大多数的国家都有具体的部门来管理频谱的使用情况,比如美国的联邦通讯委员会(FCC)[1]、中国的无线电管理局(RAB)[2].他们静态地将频谱资源以长期和大范围的形式分配给大型的无线网络提供商.这一静态分配策略造成本已稀缺的频谱资源不能得到有效的利用,具体体现在2个方面:1)静态频谱分配没有充分考虑频谱需求的空间和时间差异性,造成在很多地区、很多时间段大块的频谱资源长期处于闲置状态;2)新兴的无线网络应用由于缺乏足够的频谱资源而无法发挥其应用价值.国际通联盟(International Telecommuni-cation Union, ITU)发布的无线电使用报告中反映了这种低效率的频谱分配机制.现在频谱分配面临着如下2个困境:1)很多频谱拥有者,又称为主用户(primary users)愿意将他们空闲的频谱资源出租以获得一定的经济利益;2)新兴的无线网络服务商,又称为次级用户(secondary users)希望通过租用频谱资源来支撑其无线服务.所以,为了有效地利用有限的频谱资源,频谱资源动态二次分配变得尤为重要,新兴的认知无线电技术使频谱资源动态二次分配成为可能.设计和研究基于市场规律的频谱分配机制成为了通信网络领域亟待解决的问题.开放的频谱拍卖市场,比如Spectrum Bridge[3],已经兴起,这些市场通过对频谱资源的买、卖、出租等多种形式来进一步提高频谱资源的利用率.
在频谱分配博弈中,我们将频谱资源动态二次分配问题抽象为市场供求关系,并设计激励机制实现频谱分配优化.一个有效的频谱分配激励机制应该具备2方面的功能:1) 让频谱资源所有者愿意将其闲置的频谱资源提供给频谱资源需求者,并使频谱资源所有者在出让资源时可以获得收益;2) 引导具有自私性的频谱资源需求者有序、高效地使用可用频谱资源.
由于所具有的公平性和有效性,拍卖机制被认为是高效的资源分配机制.从1994年开始,FCC已经举办了一系列的频谱牌照拍卖,并且从中收取了巨额的收益.在欧洲,政府部门为UMTS[4]和LTE[5]频谱的使用也举办了大规模的拍卖.但是这些拍卖机制针对的是大型的无线网络服务提供者,我们的目标针对的是小规模的无线服务应用提供者,比如社区或者家庭的无线网络提供者.
设计一套灵活的、贴近实际的频谱拍卖机制存在诸多挑战,现有的频谱工作主要考虑5个挑战:
1) 防策略性(strategy-proofness)
第1个主要的挑战来自于自私用户的策略行为.在防策略性频谱拍卖机制中,简单地提交真实的频谱需求信息,包括对信道的估值和需求信道集合,能够最大化信道拍卖参与者的效益.由于拍卖参与者大多是理性和自私的,他们总是希望通过策略性地操纵拍卖来提高他们的收益.在实际的频谱交易市场中,自私的参与者不仅会谎报他们对信道的估值,也会谎报他们需求的信道集合.当报价和需求的信道集合都是买家私有信息的时候,我们称这样的买家为多策略买家.这些自私行为不可避免地会影响到其他参与者的收益,所以,如果频谱拍卖机制不能保证防策略性,将会极大地打击真实的买家参与频谱拍卖市场的积极性.现有的大部分工作并没有考虑多策略买家的拍卖模型,多策略买家拍卖机制的设计属于多参数激励机制设计的范畴.多参数激励机制设计仍然是算法博弈论(algorithmic game theory)领域内的开放型研究问题,还不存在行之有效的解决方案.文献[6-7]给出了在多参数激励机制中要满足防策略性必须要满足的条件.一些论文也讨论了负面的结果,比如文献[8-9]指出在普适的多参数组合拍卖模型中,不存在既能满足防策略性质又能有系统性能保证的组合拍卖机制.
2) 信道的空间重用性
空间重用性使得频谱资源不同于传统的拍卖商品.如果2个无线用户互相不在对方的干扰区域里,他们就能够同时使用相同的无线信道.利用频谱的空间重用性能够极大地提高频谱的利用率.
3) 信道的异质性
无线频谱资源的通信特性使得在信道拍卖中的拍卖物品具有异质性.频谱的异质性来源于2个方面:空间上的异质性和频率上的异质性.一方面,在不同的地区,信道的可用性和信道的通信质量是不同的;另一方面,具有不同中心频率的信道也具有不同的传播和穿透特性.
4) 投标的多样性
无线设备有可能配备多根天线,使得无线设备在同一时刻能够工作在多个不同的异质信道上.因此一个无线用户根据他的服务质量需求,能够同时请求多个不同的信道.更进一步地说,由于信道的异质性,买家对不同的异质信道组合会有多样化的偏好.比如一个次级网络用户有可能对某些成对的信道(用来提供LTE服务)具有较高的估值,对另外非成对的信道(用来提供WiMax服务)有较低的估值.因此,在频谱拍卖机制中允许买家对不同的信道集合可以有不同的估值.允许买家投标的多样性,可以提高买家获得信道的机会,使得频谱重分配机制更加灵活、高效.
5) 社会福利(social welfare)最大化
拍卖中最基本和普遍的优化目标是最大化社会福利,也就是获胜方对他们所分配物品估值的总和.然而,最大化社会福利通常是NP难的问题,在多项式时间内并不能得到最优解.
图1展示了运用组合拍卖的技术来解决电视白频谱重分配的问题.电视白频谱具有空间和频率上的异质性,不同地区的白频谱设备能够访问到不同的电视白频谱,并且具有不同的最大允许功率、信道干扰强度、信道噪声强度等.电视频谱的频率范围是54~806 MHz,导致了不同的白频谱具有不同的频率特性.

Fig. 1 Heterogeneous TV white space spectrum redistribution based on combinatorial auctions.图1 基于组合拍卖的异质电视白频谱重分配机制
1国内外研究现状及发展动态分析
1.1研究背景
频谱资源分配问题是移动互联网中典型的激励机制设计问题.在本节将简要地回顾移动互联网激励机制的研究背景.通过这个研究背景的介绍,我们能够更清楚地了解动态频谱重分配问题的研究动机和研究意义.
移动互联网络的迅速发展和广泛应用已改变了现代人类的生活方式,其高效运行有赖于各组网用户节点间的协同合作.以往的无线通信设备将网络协议固化在硬件中,以保证用户节点忠实地遵循网络协议.但随着无线通信设备的快速发展,以及软件无线电(software defined radio)和智能移动设备(例如智能手机和平板电脑)的广泛使用,用户可以越来越灵活地控制他们的无线通信设备.
由于移动互联网络具有分布性和自组性的特点,故其与传统的分布式自治系统(distributed autonomous system)一样面临着用户节点的自主协同问题,即用户节点的自私性所引起的网络整体性能下降.例如,搭便车问题(free-rider problem),用户节点只索取资源或服务而不贡献资源或服务;逆向选择问题(adverse selection problem),用户节点通过透露错误的信息误导系统向有利于自己的方向发展;串谋舞弊问题(collusion problem),用户节点结成小团体以谋取更大的利益.研究表明,以Gnutella为代表的分布式自治系统中有近70%的搭便车节点[10].在移动互联网络中,这种自私行为可能损害网络的连通性,降低网络的可用性.又如,本文所考虑的无线频谱资源重分配问题.认知无线电(cognitive radio)技术为有效利用闲置频谱资源提供了一种有效的途径,配备认知无线电的移动互联网络节点可共享检测到的“频谱空洞”进行通信.为了获得更大通信流量,自私的用户节点倾向于调制其认知无线电设备到尽可能宽的通信频带,或缩短信道接入时的退避等待时延以获取更长的信道使用时间.这些自私行为将会增大无线自组网络中的信号干扰,破坏通信媒介访问控制协议的公平性,从而损害移动互联网络的健壮性.
可见,如果没有有效的机制保证用户节点间的协同合作,那么用户节点的自私行为将会使移动互联网络进入无政府的混乱状态,导致网络可用性和健壮性的急剧下降.然而,移动互联网络所特有的高度动态性和连接间断性,决定了我们无法简单地利用分布式自治系统中已有的技术解决新兴的移动互联网络中的自主协同问题.所以,我们需要设计适用于移动互联网络的有效机制,以激励移动互联网络中的用户节点相互协同合作,保证移动互联网络的高效运行.
移动互联网络中自私用户节点之间的相互作用关系可以自然地抽象为博弈模型.所以,本文将以博弈论为主要工具,研究用户节点在移动互联网络中的交互行为.博弈论研究多个决策者间竞争的交互关系,以及寻求最优行为策略的数学理论和方法.以博弈论为工具开展移动互联网络合作激励机制研究具有三大优势:
1) 通过将移动互联网络中的问题形式化为策略博弈模型,我们可以利用丰富的博弈论工具分析用户节点的交互行为策略及其对网络的影响.
2) 博弈论为我们提供了在竞争环境中实现单目标和多目标优化的理论基础和可行办法.
3) 包括非合作博弈在内的许多策略博弈模型符合移动互联网络分布式动态决策的特征,其研究成果对我们设计无线网络合作激励机制提供了有力的支持.
移动互联网用户协同激励机制设计问题自2000年以来得到了国内外广大科研人员越来越高的重视.2008年以来形成了一个高潮,一些一流国际刊物纷纷推出了相关专刊,并涌现出一批由北美和欧洲著名高校和科研机构发起的高水平专门学术会议(例如Gamecomm[11],GameNets[12]和GameSec[13]).多个主流网络与通信领域的学术会议也纷纷开设相关主题的分会,同时收录的相关学术论文数量也呈上升趋势.
2000—2002年是用户协同激励机制研究的起步阶段,所采用的激励机制以简单的基于信誉的机制为主,但该领域的研究工作迅速得到了一批顶尖科研人员的关注.在随后的4年中(2003—2006年),每年都有较稳定数量的相关论文出现,这期间的研究工作大都集中在路由选择激励机制上.2007年以来,由于移动互联网和认知无线电的广泛应用,用户协同激励机制在确保无线网络正常运行(特别是无线频谱资源的公平、合理、高效的管理)中的作用也变得更加重要,也受到了更加广泛的关注.近些年,相关论文数量的急剧增长,也从一个侧面反映了目前用户协同激励机制研究的重要性.
1.2频谱分配激励机制
在本节中,我们将重点回顾频谱分配激励机制.频谱分配激励机制主要基于策略博弈(strategic game)和拍卖(auction)2种模型.
1) 基于策略博弈模型的频谱分配激励机制.该机制研究开始于对纳什均衡(Nash equilibrium)的分析.Halldorsson等人联合分析了频谱分配博弈中形成纳什均衡所带来的无秩序代价(price of anarchy)[14].Felegyhazi等人分析了多个无线应用服务提供商(service provider)竞争使用频谱资源争夺用户的问题[15].Felegyhazi等人又研究了信道分配博弈中纳什均衡的存在性问题,并提出了使信道分配博弈收敛到纳什均衡的集中式和分布式算法[16].随后,吴帆等人联合提出了一种信道分配激励机制,使信道分配博弈能够一步收敛到强占优策略均衡(strongly dominant strategy equilibrium),并最大化此均衡状态下整个系统的吞吐量[17-18].王新兵等人提出了一种防串谋性纳什均衡,并证明了其在频谱分配博弈中的存在性[19].张黔等人率先研究了一个三层频谱分配市场模型中纳什均衡的存在性[20].Kasbekar和Sarkar利用重复博弈模型研究了认知无线电网络中的信道有偿转让问题,并明确给出了纳什均衡的构造方法[21].2011年吴帆等人提出了一种适应动态可调信道的频谱分配激励机制[22],该激励机制能够使频谱分配一步收敛到占优策略均衡(dominant strategy equilibrium),并最大化整个无线网络的吞吐量.在自私的参与者中进行资源分配问题已经在不同的网络环境中得到了广泛的研究,比如无线网状网络[23]、OFDMA蜂窝网络[24]和LTE网络[25].
2) 基于拍卖模型的频谱分配激励机制.该机制以Zhou等人提出的VERITAS[26]和TRUST[27]为代表.VERITAS采用了类似于eBay的拍卖模式,让网络节点竞标频谱资源,并根据各节点的出价情况决定得标者及其需支付的费用.VERITAS既保证了频谱拍卖的防策略性,又在一定程度上提高了频谱的空间利用率.TRUST创造性地将频谱分配和复式拍卖(double auction)相结合,有效防止了频谱资源出售和需求双方面的自私行为,但存在频谱利用率低的问题.随后,吴帆等人提出了一种新型的保留价频谱拍卖机制SMALL[28].SMALL既能保证频谱拍卖的防策略性,又能弥补VERITAS和TRUST频谱利用率较低的不足.此外,张黔等人提出了一种基于VCG(由Vickrey[29],Clarke[30]和Groves[31]的开创性工作而得名)的频谱拍卖机制[32].Zhou和Zheng还研究频谱拍卖中的串谋舞弊问题,并提出Athena[33]为频谱拍卖提供强度可调的串谋防控机制.最近,王新兵等人创造性提出了一种基于组合拍卖(combinatorial auction)的信道分配机制[34].除此之外,在信道拍卖上还有一些其他的相关工作,比如在线信道拍卖机制[35]、信道拍卖中的利润最大化问题[32].考虑到求解最优解的较高的时间复杂度,针对不同的信道干扰模型和买家的不同的估值函数形式,研究人员提出了多种有效的近似算法[36-37].我们在这方面也做了一些创造性的工作,比如异质频谱拍卖算法[38-39],具有隐私保护功能的频谱拍卖算法[40].
近年来,研究者开始关注基于在线拍卖(online auction)的频谱接入激励机制.美国伊利诺伊理工大学李向阳领导的WINET研究组在在线频谱拍卖和激励机制设计上有着深入的研究[41-46].在文献[42]中作者对单纯用户的频谱接入行为进行分析,并设计了在线频谱分配与收费机制,使总社会效益最大化.当用户到达服从泊松分布时,TODA[41]在线拍卖机制能够取得线下(off-line)VCG拍卖机制社会效益的80%和频谱使用率的70%.SALSA[45]在2种用户到达模型(半随机到达模型与随机到达模型)下,取得了社会效益和预期收入的同步近似最大化.SOFA[42]对竞标人在到达之后的竞标时间和中间拍卖方的决策时间作了限制,并规定获胜方只能获得单个信道,进而在可抢占的情况下使得拍卖系统取得纳什均衡.TOFU[43]在SOFA的基础上,使得自私的用户不能通过低价竞标的方式获益,且取得总收入相比线下VCG拍卖机制的比例大于95%,他们还考虑了多信道在线拍卖.杨耀宇和龙承念等人在考虑时间和空间可重用的情况下,利用在线市场结算(online market clearing)方法针对动态冲突图(dynamic conflict graph)设计结算规则[47].Deek等人设计的Topaz[35]应用了三维打包(3D bin packing)技术,将时间、空间、频率分布同时考虑进行分配,采用基于临界值的收费方法,保证媒介接入在线拍卖的可信性.
1.3拍卖机制设计
在本节中,我们着重回顾了博弈论中拍卖机制设计的相关工作.拍卖机制设计是博弈论中的重要分支,而其中组合拍卖机制又是拍卖机制领域的研究热点.在过去的10年中,诸多学者针对不同的模型,提出了多种组合拍卖机制.Dobzinski[48],Buchfuhrer等人[49]和Papadimitriou等人[50]证明了在普适的组合拍卖模型中最优社会福利和防策略性不能够同时达到.Lehmann甚至断言在多策略的买家模型中,任何贪心的分配算法都无法保证防策略性[51].
考虑到组合拍卖问题的计算复杂性,众多研究学者提出具有近似比和防策略性的组合拍卖机制[52-54].在文献[55]中,作者将信道在时间和频谱维度上分配问题建模成单策略的组合拍卖问题,并且提出了一个基于贪心分配方法来达到近似最优社会福利.但是以上所有的组合拍卖机制并没有考虑频谱的空间重用性,因此不能直接运用到动态频谱分配中.
拍卖机制已经被广泛地运用于各种不同形式的资源分配问题,比如云计算中的资源分配问题[56-57]、移动参与式感知中的任务分配问题[58-59]和社交网络中的动态合作问题[60].除了拍卖机制之外,一些强有力的工具,比如契约理论[61]、排队理论[62]和随机算法设计[37],都被运用到了频谱市场设计的各个方面.
1.4博弈论概念简介
在本节中,我们简要地描述在动态频谱管理研究中经常使用到的相关博弈论知识.
在博弈论里一个很重要的概念是占优策略.
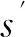
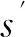
占优策略的概念是激励相容(incentive com-patibility)性质的基础,在直接揭示的拍卖中,激励相容的性质意味着对于任何的买家没有激励来使他对他的私有信息进行撒谎,因此真实地反应出他的信息是每个买家的占优策略.一个伴随的概念是个人理性(individual rationality),这意味着每一个参与游戏的玩家都希望得到的收益能够不少于他不参加游戏所能得到的收益.我们现在引入防策略性机制(strategy proof mechanism)定义.
定义2. 防策略性机制[65-66].一个机制是防策略性的,当它满足激励相容和个人理性.
2目前频谱拍卖存在的问题
虽然近些年来涌现出不少频谱资源重分配的研究成果,但我们认为这些工作普遍存在着模型失真、均衡失判、机制失信、分布失控4大问题.
1) 模型失真
博弈模型是开展动态频谱资源重分配的基础,但多数已有工作为了让问题可解,在博弈模型的构建过程中引入了过多理想化的假设.如假设组网节点同构,具有相同的处理能力、传输速率、发射功耗等;又如,假设通信信道同质,具有相同的带宽、噪声和干扰强度等.这种让问题适应解法的研究方式,势必导致研究成果的实用性大大降低.
2) 均衡失判
多数已有工作止步于分析纳什均衡的存在性,然而给定一个博弈模型,纳什均衡往往并不是唯一的,不同纳什均衡带来的系统整体性能往往也是不同的.当有多个纳什均衡存在时,如何判别不同纳什均衡的优劣,有待进一步研究.纳什均衡的存在,并不等价于系统能够在有限时间内收敛到纳什均衡,从而纳什均衡的收敛性也是我们需要研究的问题.
3) 机制失信
纳什均衡是博弈论中相对脆弱的解决方案概念(solution concept),当存在多个纳什均衡时,参与者仍然可能通过操纵博弈过程,使系统收敛到对其较有利的纳什均衡状态.然而,能够达到占优策略均衡或防策略性的高强度激励机制还不多.
4) 分布失控
已有的激励机制大都依赖于一个可信第三方(或中心控制)来保证机制的可信性,如负责虚拟货币结算的中心银行和记录声誉分数的信誉中心.这种集中式的控制方式不适用于分布式的网络环境,导致在分布式网络中可行的方案只剩下物物直接交换.显然,物物交换不利于网络信息传播与服务传递的灵活性.现有的频谱拍卖机制大都需要有一个可信的中心节点来负责拍卖的有序进行.
3频谱动态管理中的关键学科问题
针对第2节所述模型失真、均衡失判、机制失信、分布失控4大问题,动态频谱管理的研究将紧密围绕以下关键科学问题展开:
1) 准确博弈模型的构建(研究模型失真问题)
博弈模型是从现实网络环境中高度抽象出来的数学模型.博弈模型描述了参与者(用户节点)的利益趋向和在博弈中的理性行为策略,并决定了参与者的行为策略所产生的最终博弈结果.构建能够准确反映复杂频谱管理系统中的博弈模型是研究和设计频谱拍卖机制的基础所在.一个博弈模型由参与者效用函数(payoffutility function)和参与者策略集合(set of strategies)两个主要部分组成.效用函数反映了参与者在博弈中的利益趋向;策略集合反映了参与者的行为空间.准确选取效用函数和策略集合对准确判断参与者的行为目标、分析博弈均衡状态及设计切实有效的激励机制至关重要.
2) 纳什均衡的存在性、唯一性和收敛性(研究均衡失判问题)
给定一个无线网络博弈问题或者具体的频谱重分配问题,我们首先关心的是在没有外界因素影响的条件下该博弈中是否存在纳什均衡.如果存在,纳什均衡是否唯一.当存在多个纳什均衡时,需要判断各个纳什均衡的优劣.给定评判标准,是否存在一个最优的纳什均衡.当存在最优纳什均衡时,系统如何收敛到一个最优纳什均衡,以及收敛的时间开销和通信开销如何评估将是一个重要的问题.
3) 强激励机制的存在性与设计(研究机制失信问题)
纳什均衡是一种相对较脆弱的解决方案概念,脆弱的原因有3个:
① 纳什均衡对某一参与者遵循其均衡策略的激励作用,建立在所有其他参与者都遵循他们相应的均衡策略的假设基础上.而当上述假设不能得到保证时,纳什均衡则无法对参与者产生任何激励作用.
② 网络系统在达到纳什均衡时,其性能往往不能达到最优化.例如,系统吞吐量没达到最大化,或路由选择的路径非最低功耗路径.由于网络系统的纳什均衡状态往往并不唯一,某些自私节点为了最大化个人利益,会故意引导网络系统收敛到对其有利的纳什均衡状态,导致网络整体性能受损.
③ 网络系统收敛到纳什均衡的过程往往非常慢长.在某些情况下,网络系统甚至无法收敛到一个纳什均衡状态,而在多个状态之间来回震荡.
为了克服纳什均衡的弱点,我们将以最优化社会效益(social efficiency)为目标,分析各种无线网络博弈激励机制在理论上能够达到的最高强度.例如,常见解决方案概念强度由高到低排序如下:占优策略均衡、贝叶斯纳什均衡(Bayesian Nash equilibrium)、纳什均衡.目前,在激励机制最高可实现强度方面的研究结果还存在很大的空白,导致大多数现有激励机制的强度是否达到了理论上的最高强度并不明确.本文的研究将填补这一空白.
在激励机制设计方面,一个高效的、可信的强激励机制应具备3个特性:①每个参与者的最优策略不依赖于任何其他参与者使用的策略;②系统在达到均衡状态时,社会效益得到最优化;③系统可一步收敛到均衡状态.
4) 可信第三方的依赖性(研究分布失控问题)
已有的激励机制大都依赖于一个可信第三方的全程参与,以保证激励机制达到理想的强度.例如,基于拍卖的动态频谱分配激励机制有赖于一个可信的拍卖商的全程参与.然而,在分布式的无线网络环境中,往往不存在一个可信的实体能够掌握整个网络的信息,充当拍卖商的角色.所以,一个实用的激励机制应该适应分布式的无线网络环境.
4可行的研究方案
针对现有工作存在的问题,我们认为应该采用策略博弈模型(strategic game model)及扩展博弈模型(extensive game model)来研究动态频谱分配中的用户行为.所用到的主要解决方案概念及其强度关系由图2所示.需要说明的是,我们将采用的解决方案概念将不局限于本节所列,将在具体研究过程中选择合适的解决方案概念作为激励机制设计的目标.

Fig. 2 The relation of solution concepts.图2 解决方案概念强度关系
纳什均衡和子博弈精炼均衡(subgame perfect equilibrium)是博弈论中强度相对最弱的均衡状态.在纳什均衡状态中,给定其他参与人的策略组合,任何参与人都无法通过仅调整其自身策略实现提高个人收益的目的.给定一个子博弈精炼均衡,在其任何一个子博弈中均是一个纳什均衡.
强帕累托最优均衡比纳什均衡和子博弈精炼均衡的强度略高.在强帕累托最优均衡中,不存在另一个策略组合可以在不使任何其他参与者收益变差的前提下使至少一个参与者的收益增加.
5基于组合拍卖的异质频谱重分配机制
基于第4节所概括的可行研究方案,我们将展示一个具体的频谱拍卖机制,该机制能达到最高强度的均衡,即(严格强)占优策略均衡.
5.1问题形式化定义
本节我们将给出异质频谱拍卖问题的拍卖模型,并提出虚拟信道的概念.通过虚拟信道,我们能够将异质频谱拍卖的问题转化为传统的组合拍卖问题.
5.1.1拍卖模型
我们考虑的是一个静态的频谱拍卖场景,其中有一个主用户,我们称之为卖家,想用通过出售他临时空闲的无线信道资源来获得一定的收益.同时一些次级用户(比如WiFi热点),我们称之为买家,想要租借主用户的空闲信道来提供一定质量的无线服务.由于诸多原因,比如背景噪声、环境温度和地形等,信道会产生差异性,所以这里我们采用的是异质信道模型.由于我们考虑的是异质信道拍卖的场景,用户对不同的信道会有自己不同程度的偏好.鉴于无线网络设备能够配备多根不同的天线,根据买家的需要,买家能够请求多于一个的信道.考虑到买家偏好的多样性和信道的异质性,我们允许买家能够提交多个不同的信道集合,这其中只能有一个信道集合能够被分配给买家.在本文中,我们假定买家对他们请求的信道集合具有统一的估值.这是因为买家请求的任何一个信道集合都能够满足买家的服务需求.不同于传统物品的拍卖,无线信道具有空间重用性,意味着在空间上离得足够远的用户相互之间不会产生干扰,因此他们能够同时工作在同一个信道上.
我们将异质信道重分配的过程建模成一个组合拍卖模型.买家同时提交报价和信道需求给一个可信的拍卖商,这样任何一个买家就不能知道其他买家的私有信息.拍卖商根据提交的报价和信道需求进行信道分配的决策,确定获胜买家,并计算每个获胜买家的费用.我们将频谱市场中用来交易的异质且正交的m个信道表示成:C={c1,c2,…,cm}.我们将买家集合表示成:N={1,2,…,n}.我们将组合频谱拍卖模型用到的主要实体定义如下:
1) 信道需求Ri.每一个买家i∈N提交一个需求的信道集合向量给拍卖商:
2) 估价vi.买家i对于自己的信道集合向量中的任意一个信道集合的估价都相同,记为vi.对信道的估价是买家i的私有信息.买家的估价满足2个性质:覆盖支配(free disposal)和规范化(normalization).覆盖支配表示的是对于任意2个信道集合S和T,如果S⊆T,则我们有vi(S)≤vi(T);规范化指的是对于∅买家的估价为0,也就是vi(∅)=0.我们表示所有买家的估价为
3) 报价bi.每一个买家i∈N可以向拍卖商提交一个报价bi,表示如果他获得任意一个需求的信道集合,他愿意为此付不多于bi的价格.在这里,我们注意到买家的报价bi并不一定要等于他的估价vi.我们将所有买家的报价表示为
4) 支付费用pi.拍卖商对每一个获胜的买家要收取一定的费用,记为pi.输家不会被收取任何费用.我们用向量
来表示所有买家的支付费用.
5) 收益ui.一个买家的收益被定义为他对获胜的信道集合的估价和他的支付价格之差.表示为
ui=vi-pi.
我们考虑的拍卖模型是买家是理性的且自私的情况,因此他们的目标是最大化自己的收益.相比于买家的目标,拍卖商的目标是最大化整个市场的社会福利.我们将社会福利定义如下:
定义3. 社会福利.在无线频谱拍卖中,社会福利被定义为所有获胜买家对他们竞标得到的信道集合的估价的总和,表示为
其中,W是所有获胜买家的集合.
在本设计中,我们假设所有的买家互相之间并不串谋,并且他们不会欺骗自己需求信道集合,我们将这些开放性的研究问题作为我们的后续工作.
5.1.2虚拟信道
不同于已有的信道拍卖机制,我们将介绍一个创新性的概念:虚拟信道(virtual channel),来刻画买家在信道使用上的冲突情况.通过引入虚拟信道,我们将异质信道的拍卖模型转化为传统的组合拍卖模型.然而传统的组合拍卖模型仍然存在较高的时间复杂度,所以在接下来的讨论中我们将提出满足防策略性且具有较好近似比的组合拍卖机制,以此来解决异质信道的动态重分配问题.

算法1. 虚拟信道分配算法.
输入:冲突图集合G、信道需求向量R;
输出:虚拟信道集合VC、更新的信道需求向量R′.
①VC←∅,R′←R;
② for eachGk=(Ok,Ek)∈Gdo
③ for each(i,j)∈Ekdo




⑧ end for

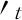




我们给出虚拟信道的正式定义:

在大多数已有的信道拍卖的工作中[26-27],基本都是采用单一的冲突图来表示买家在信道使用上的冲突关系.但是,在异质信道的情况下,每一个信道都会有一个不同的冲突图.我们用Gk=(Ok,Ek)来表示在信道ck上的冲突图,这里Ok⊆N表示的是能够使用信道ck的所有用户的集合,每一条边(i,j)∈Ek表示的是买家i和买家j在信道ck上的冲突关系.我们用G={Gk|ck∈C}来表示所有冲突图的集合.我们还将所有冲突图中最大的度记为δ.频谱拍卖商能够通过一些实际的测量方法,比如测量校准的方法[68]来获得每个信道上的冲突图.我们注意到我们使用的冲突图的建模方法属于二元的干扰模型,比如协议模型.也有另外一些文章考虑的是在物理干扰模型中的无线频谱重分配问题,更多讨论请参见文献[36-37].


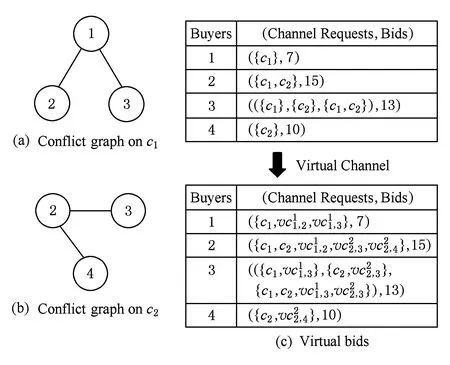
Fig. 3 An example showing the generation of virtual channels.图3 展示虚拟信道形成的示例
5.1.3问题定义
借助上述虚拟信道,我们现在可以将异质信道的动态重分配问题转化为一个经典的组合拍卖问题.拍卖算法的输出为获胜买家的集合和他们被分配到的信道集合.
目标函数:

限制条件:
(1)
(2)
(3)
在这里限制条件式(1)表示了虚拟信道的数量限制.由于我们已经从更新的信道集合中移除了所有的原始信道集合,我们并没有考虑原始的信道集合.限制条件式(2)表明了每一个买家最多能够从他需求的信道集合中获得一个信道集合.限制条件式(3)表明了拍卖商的决策变量的取值.
如果最优的社会福利能够通过解决以上的二元整数规划得到的话,那么我们就可以通过传统的VCG拍卖机制来计算支付价格,并保证机制的防策略性.但是,以上的二元整数规划问题能够在多项式时间内通过精确覆盖问题规约过来,故能够被证明是NP-Hard的问题.考虑到二元整数规划问题在计算上的时间复杂程度,在5.2节中,我们将提出一个贪心的信道分配机制来达到近似最优社会福利.我们会进一步将贪心分配方法和一个定价机制结合起来设计具有防策略性和较好近似比的异质信道组合拍卖机制.
5.2异质频谱拍卖机制
本节我们考虑的是不可分的信道拍卖市场,也即信道只能够以整体的形式分配给没有冲突的买家,我们并没有考虑时分复用信道的情况.在5.1节中,我们知道寻找最优的信道分配策略在多项式时间内是不能达到的.所以,在本节中,我们假设买家对他们需求的信道集合的估价是统一的,基于该假设我们提出了一个基于组合拍卖模型的异质频谱拍卖机制,该机制满足了防策略性,并取得了近似最优的社会福利.
我们设计的机制包含了3个主要的部分:虚拟信道的形成、获胜买家的确定和支付价格的计算.我们先简要地介绍机制的设计思想:1)我们生成虚拟信道来刻画买家在无线信道上的使用干扰,并且将无线信道重分配的问题转化为互斥虚拟信道的分配问题;2)我们提出了贪心算法来确定获胜的买家,该贪心算法能够获得较好的近似比;3)我们设计了基于临界报价的支付价格计算方案来保证频谱拍卖机制的经济学性质.
5.2.1虚拟信道生成
虚拟信道的生成过程和算法1是一样的,我们另外向每个买家i∈N的每个需求的信道集合中添加一个虚拟信道vci.虚拟信道vci是用来确保买家i最多能够被分配一个需求信道集合.

VC=V∪{vci|i∈N}
5.2.2获胜买家的确定

信道分配算法将所有的买家根据他们的虚拟报价进行非升序排列:
对于虚拟报价相等的情况,算法将依据以报价无关的原则来打破这种情况,比如买家标示符的字典序或者信道编号.根据L1的排序,算法将按序给每位买家分配最小的信道集合.
算法2. 确定获胜买家的近似算法.
输入:更新的信道需求向量R′、报价向量B;
输出:获胜买家和被分配的信道集合(W,S).
① (W,S)←(∅,∅),M←∅;
② for eachi∈Ndo

④ end for

⑥ fori=1 tondo
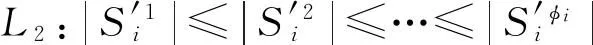
⑧ forl=1 toφido


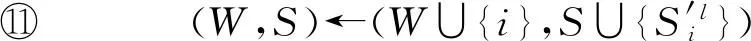




算法2展示了上述确定获胜买家过程的伪代码.在实际频谱交易场景中,买家的人数n远大于参数Φ,因此算法2的时间复杂度为O(nlogn).
5.2.3支付价格的计算
支付价格的计算基于临界的虚拟报价,其定义如下:
定义5. 临界的虚拟报价(virtual critical price).对于买家i∈N,其临界的虚拟报价cr(i)∈L1被定义为买家i想要获得需求的信道必须出的最低虚拟报价,也就是说,如果买家出的虚拟报价大于cr(i),他就会获胜,反之他就失败.
我们注意到根据临界虚拟报价的定义,无论买家i被分配了哪个具体的信道集合,他的临界虚拟报价cr(i)始终是一样的.
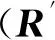
1) 如果买家i在拍卖中失败了,或者临界虚拟价格cr(i)不存在(用cr(i)=0来表示),那么他的支付价格就为0.
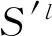
我们可以证明设计的算法能够满足防策略性,并且可以获得比较好的近似比.给出如下2个定理,具体的证明可以参见文献[38].
定理1. 针对不可分的异质信道重分配问题,我们设计的组合频谱拍卖机制满足防策略特性.
定理2. 我们提出的组合频谱拍卖机制的近似比是O(δm),其中δ是所有冲突图中的最大度,m是信道的数量.
5.3实验结果
5.3.1仿真方法
我们实现了机制SMASHER并将它和机制TAHES[67]和CRWDP[34]进行对比.所有的买家被随机地分布在一个1 000 m×1 000 m的方形里,买家的数量以20为增量从20增加到400.被分配的信道可以是以下3个值:6,12和24.异质信道可以有不同的干扰半径,从250~450 m.在我们的拍卖过程中,我们允许买家可以具备不同数量的天线,但是限制最大的需求信道集合为3.我们假设买家对信道的估价是在(0,1]区间上均匀分布的,我们考虑单需求买家的情形(如Φ=1)和多需求买家的情形,此时买家最多能够提交3个不同的信道子集(如Φ=3).我们所有的实验结果都是取了200次的平均,所有的参数都可以不同于这里的取值,但是使用不同的参数所得到的仿真结果的规律是类似的.因此,在本文中我们仅仅展示这些参数下的实验结果.
我们衡量如下的3个指标:
1) 社会福利.社会福利是获胜买家对他们分配到的信道集合的总和.
2) 满意度.满意度指的是获胜用户的百分比.
3) 信道利用率.信道利用率是每个信道被分配到的天线的平均个数.
5.3.2SMASHER机制的性能
我们将机制SMASHER的性能和2个不同的防策略性异质信道拍卖机制TAHES和CRWDP进行比较.我们验证了机制在单需求用户(Φ=1)和多需求用户(Φ=3)下的实验结果.我们也验证了在误差率为10-4时的最优结果,并把它记为IP-OPT.该最优解能够通过求解0-1整数规划来得到,并把它作为算法的上界.
图4表示了当有12个拍卖信道时的仿真结果,买家的人数是变化的.我们能够看到,机制SMASHER总是比其他任何2个拍卖机制都优,并且逼近最优值,特别是当用户是单需求的情况Φ=1.当买家的数目小于60时,机制TAHES不能够形成拥有大量报价的有效的买家分,因此在这些条件下表现比较差;当买家的数目大于60时,机制CRWDP不是很好,因为机制CRWDP没有考虑信道的空间重用性,也就是在所有情况下机制CRWDP的信道利用率都是1.图4也表示了当买家的数量上升时社会福利和信道的利用率也会上升,但是满意度下降了.一方面,更多的买家会导致在有限的信道上有更激烈的竞争,因此降低了满意度;另一方面,机制SMASHER能够在更多的买家中更有效率地分配信道,因此社会福利和信道利用率会升高.

Fig. 4 Performance when there are 12 channels.图4 当信道数量为12时的系统性能
图5展示了当有200个买家并且拍卖的信道数量是6,12,24时的实验结果.我们可以再一次看到,机制SMASHER总是会比机制TAHES和CRWDP有更好的效果,不管是在单需求买家Φ=1或者是多需求买家Φ=3的情况下.图5也展示了当拍卖信道的数量上升时社会福利和满意度是上升的,但是信道利用率是下降的.原因是更多的交易信道会导致在拍卖中更多的成交量,当买家的数量固定时社会福利和满意度就会增加;信道的利用率降低是因为当信道的数量提升时买家的天线能够被分配在更多不同的信道上.

Fig. 5 Performance when there are 200 buyers.图5 当买家数量为200时的系统性能
从图4和图5我们能够看到,机制SMASHER牺牲了少量的系统性能来保证经济性质上的鲁棒性.虽然机制IP-OPT能够达到近似的最优社会福利,但是我们并不能直接将其用在信道重分配中,因为机制IP-OPT对经济性质没有任何保证.我们观察到机制SMASHER在多需求用户的情况下的系统性能总是会好于机制SMASHER在单需求用户的情况.这是因为多需求的买家比单需求的买家有更大的机会获得信道,这会导致在拍卖中更多的交易.因此,允许买家提交多份频谱需求确实能够提高拍卖的系统性能.
6结束语
在本文中,我们从博弈论的角度出发,对异质频谱重分配的问题进行了系统的调研和研究,指出现有工作存在的问题,并提出可行的解决方案.在次级频谱市场中,我们假定无线网络中的节点是策略性的玩家,拥有自身的利益,通过相互竞争来获得有限的频谱资源.我们采用拍卖机制来设计高效、有序的频谱分配方案.我们指出一套灵活高效的频谱拍卖机制需要考虑5个主要的设计难点:用户自私策略行为、信道的异质性、信道的空间重用性、用户偏好的多样性和社会福利的最大化.结合这5个设计挑战,我们提出了一套高效的信道拍卖机制,证明了该机制满足防策略性且能够达到较好的近似比.
参考文献
[1]Wheeler T. Federal Communications Commission(FCC)[EBOL]. 2000 [2015-10-10]. http:www.fcc.gov
[2]Miao Wei. Radio Administration Bureau (RAB)[EBOL]. 2002 [2015-10-10]. http:wgj.miit.gov.cn
[3]Stanforth P. Spectrum Bridge[EBOL]. 2010 [2015-10-10]. http:www.spectrumbridge.comHome.aspx
[4]Klemperer P. How (not) to run auctions: The European 3G telecom auctions[J]. European Economic Review, 2002, 46(4): 829-845
[5]Taga K. LTE Spectrum and Network Strategies[EBOL]. 2010 [2015-10-10]. http:www.adlittle.comdownloadstx_adlreportsADL_LTE_Spectrum_Network_Strategies.pdf
[6]Archer A, Kleinberg R. Truthful germs are contagious: A local to global characterization of truthfulness[C]Proc of the 9th ACM Conf on Electronic Commerce. New York: ACM, 2008: 340-366
[7]Rochet J C. A necessary and sufficient condition for rationalizability in a quasi-linear context[J]. Journal of Mathematical Economics, 1987, 16(2): 191-200
[8]Dobzinski S. An impossibility result for truthful combinatorial auctions with submodular valuations[C]Proc of the 43rd Annual ACM Symp on Theory of Computing. New York: ACM, 2011: 139-148
[9]Lehmann D, O’allaghan I L, Shoham Y. Truth revelation in approximately efficient combinatorial auctions[J]. Journal of the ACM, 2002, 49(5): 577-602
[10]Adar E, Huberman A B. Free riding on Gnutella[J]. First Monday, 2000, 5(10)
[11]Eduard J. The 4th Int ICST Workshop on Game Theory in Communication Networks (Gamecomm)[EBOL]. 2011 [2015-10-10]. http:www.game-comm.org2011index.shtml
[12]Vasilakos A. The 2nd Int ICST Conf on Game Theory for Networks (GameNets)[EBOL]. 2002 [2015-10-10]. http:gamenets.org2011
[13]Panaousis M. The 6th Conference on Decision and Game Theory for Security (GameSec)[EBOL]. 2015 [2015-10-10]. http:www.gamesec-conf.org
[14]Halldorsson M M, Halpern J Y, Li Li, et al. On spectrum sharing games[C]Proc of the 23rd Annual ACM Symp on Principles of Distributed Computing (PODC 2004). New York: ACM, 2004: 107-114
[15]Felegyhazi M, Hubaux J P. Wireless operators in a shared spectrum[C]Proc of the 25th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2006). Piscataway, NJ: IEEE, 2006: 1-11
[16]Felegyhazi M, Cagalj M, Bidokhti S S, et al. Non-cooperative multi-radio channel allocation in wireless networks[C]Proc of the 26th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2007). Piscataway, NJ: IEEE, 2007: 1442-1450
[17]Wu Fan, Zhong Sheng, Qiao Chunming. Globally optimal channel assignment for non-cooperative wireless networks[C]Proc of the 27th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2008). Piscataway, NJ: IEEE, 2008: 1543-1551
[18]Wu Fan, Zhong Sheng, Qiao Chunming. Strong-incentive, high-throughput channel assignment for noncooperative wireless networks[J]. IEEE Trans on Parallel and Distributed Systems, 2010, 21(12): 1808-1821
[19]Gao Lin, Wang Xinbing. A game approach for multi-channel allocation in multi-hop wireless networks[C]Proc of the 9th ACM Int Symp on Mobile Ad Hoc Networking and Computing. New York: ACM, 2008: 303-312
[20]Jia Juncheng, Zhang Qian. Competitions and dynamics of duopoly wireless service providers in dynamic spectrum market[C]Proc of the 9th ACM Int Symp on Mobile Ad Hoc Networking and Computing. New York: ACM, 2008: 313-322
[21]Kasbekar S G, Sarkar S. Spectrum pricing games with bandwidth uncertainty and spatial reuse in cognitive radio networks[C]Proc of the 11th ACM Int Symp on Mobile Ad Hoc Networking and Computing. New York: ACM, 2010: 251-260
[22]Wu Fan, Singh N, Vaidya N, et al. On adaptive-width channel allocation in non-cooperative, multi-radio wireless networks[C]Proc of the 30th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2011). Piscataway, NJ: IEEE, 2011: 2804-2812
[23]Duarte F B P, Fadlullah M Z, Vasilakos V A, et al. On the partially overlapped channel assignment on wireless mesh network backbone: A game theoretic approach[J]. IEEE Journal on Selected Areas in Communications, 2012 30(1): 119-127
[24]Lopez-Perez D, Chu Xiaoli, Vasilakos V A, et al. Power minimization based resource allocation for interference mitigation in OFDMA femtocell networks[J].IEEE Journal on Selected Areas in Communications, 2014, 32(2): 333-344
[25]Lopez-Perez D, Chu Xiaoli, Vasilakos A V, et al. On distributed and coordinated resource allocation for interference mitigation in self-organizing LTE networks[J]. IEEEACM Trans on Networking, 2013, 21(4): 1145-1158
[26]Zhou Xia, Gandhi S, Suri S, et al. eBay in the sky: Strategy-proof wireless spectrum auctions[C]Proc of the 14th ACM Int Conf on Mobile Computing and Networking (MobiCom 2008). New York: ACM, 2008: 2-13
[27]Zhou Xia, Zheng Haitao. TRUST: A general framework for truthful double spectrum auctions[C]Proc of the 28th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2009). Piscataway, NJ: IEEE, 2009: 999-1007
[28]Wu Fan, Vaidya N. SMALL: A strategy-proof mechanism for radio spectrum allocation[C]Proc of the 30th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2011). Piscataway, NJ: IEEE, 2011: 81-85
[29]Vickrey W. Counterspeculation, auctions, and competitive sealed tenders[J]. Journal of Finance, 1961, 6(1): 8-37
[30]Clarke E. Multipart pricing of public goods[J]. Public Choice, 1971, 11(1): 17-33
[31]Groves T. Incentives in teams[J].Econometrica, 1973, 41(4): 617-663
[32]Jia Juncheng, Zhang Qian, Zhang Qin, et al. Revenue generation for truthful spectrum auction in dynamic spectrum access[C]Proc of the 10th ACM Int Symp on Mobile ad Hoc Networking and Computing (MobiHoc 2009). New York: ACM, 2009: 3-12
[33]Zhou Xia, Zheng Haitao. Breaking bidder collusion in large-scale spectrum auctions[C]Proc of the 11th ACM Int Symp on Mobile Ad Hoc Networking and Computing (MobiHoc 2010). New York: ACM, 2010: 121-130
[34]Dong Mo, Sun Gaofei, Wang Xinbing, et al. Combinatorial auction with time-frequency flexibility in cognitive radio networks[C]Proc of the 31st IEEE Int Conf on Computer Communications (IEEE INFOCOM 2012). Piscataway, NJ: IEEE, 2012: 2282-2290
[35]Deek L, Zhou Xia, Almeroth K, et al. To preempt or not: Tackling bid and time-based cheating in online spectrum auctions[C]Proc of the 30th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2011). Piscataway, NJ: IEEE, 2011: 2219-2227
[36]Hoefer M, Kesselheim T, Vöcking B. Approximation algorithms for secondary spectrum auctions[C]Proc of the 23rd Annual ACM Symp on Parallelism in Algorithms and Architectures (SPAA 2011). New York: ACM, 2011: 177-186
[37]Hoefer M, Kesselheim T. Secondary spectrum auctions for symmetric and submodular bidders.[C]Proc of the 13th ACM Conf on Electronic Commerce (EC 2012). New York: ACM, 2012: 9-19
[38]Zheng Zhenzhe, Wu Fan, Chen Guihai. SMASHER: A strategy-proof combinatorial auction mechanism for heterogeneous channel redistribution[C]Proc of the 14th ACM Int Symp on Mobile Ad Hoc Networking and Computing (MobiHoc 2013). New York: ACM, 2013: 305-308
[39]Zheng Zhenzhe, Wu Fan, Tang Shaojie, et al. Unknown combinatorial auction mechanisms for heterogeneous spectrum redistribution[C]Proc of the 15th ACM Int Symp on Mobile Ad Hoc Networking and Computing (MobiHoc 2014). New York: ACM, 2014: 3-12
[40]Huang Qianyi, Tao Yixin, Wu Fan. SPRING: A strategy-proof and privacy preserving spectrum auctionmechanism[C]Proc of the 32nd IEEE Int Conf on Computer Communications (IEEE INFOCOM 2013). Piscataway, NJ: IEEE, 2013: 827-835
[41]Wang Shiguang, Xu Ping, Xu Xiaohua, et al. TODA: Truthful online double auction for spectrum allocation in wireless networks[C]Proc of 2010 IEEE Symp on Dynamic Spectrum Access Networks (DySPAN 2010). Piscataway, NJ: IEEE, 2010: 1-10
[42]Xu Ping, Li Xiangyang. SOFA: Strategyproof online frequency allocation for multihop wireless networks[C]Proc of the 20th Int Symp on Algorithms and Computation (ISAAC 2009). Piscataway, NJ: IEEE, 2009: 311-320
[43]Xu Ping, Li Xiangyang. TOFU: Semi-truthful online frequency allocation mechanism for wireless networks[J].IEEEACM Trans on Networking, 2011, 19(2): 433-446
[44]Xu Ping, Li Xiangyang, Tang Shaojie. Efficient and strategyproof spectrum allocations in multichannel wireless networks[J]. IEEE Trans on Computers, 2011, 60(4): 580-593
[45]Xu Ping, Wang Shiguang, Li Xiangyang. SALSA: Strategyproof online spectrum admissions for wireless networks[J]. IEEE Trans on Computers, 2010, 59(12): 1691-1702
[46]Xu Ping, Xu Xiaohua, Tang Shaojie, et al. Truthful online spectrum allocation and auction in multi-channel wireless networks[C]Proc of the 30th IEEE Int Conf on Computer Communications (IEEE INFOCOM 2011). Piscataway, NJ: IEEE, 2011: 26-30
[47]Yang Yaoyu, Wu Jie, Long Chengnian, et al. Online market clearing in dynamic spectrum auction[C]Proc of 2011 IEEE Global Telecommunications Conf (GLOBECOM 2011). Piscataway, NJ: IEEE, 2011: 1-5
[48]Dobzinski S. An impossibility result for truthful combinatorial auctions with submodular valuations[C]Proce of the 43rd Annual ACM Symp on Theory of Computing (STOC 2011). New York: ACM, 2011: 139-148
[49]Buchfuhrer D, Dughmi S, Fu Hu, et al. Inapproximability for VCG-based combinatorial auctions[C]Proc of the 21st Annual ACM-SIAM Symp on Discrete Algorithms (SODA 2010). New York: ACM, 2010: 518-536
[50]Papadimitriou C, Schapira M, Singer Y. On the hardness of being truthful[C]Proc of the 49th Annual IEEE Symp on Foundations of Computer Science (FOCS 2008). Piscataway, NJ: IEEE, 2008: 250-259
[51]Lehmann D, Oc'allaghan L I, Shoham Y. Truth revelation in approximately efficient combinatorial auctions[J]. Journal of the ACM, 2002, 49(5): 577-602
[52]Bartal Y, Gonen R, Nisan N. Incentive compatible multi unit combinatorial auctions[C]Proc of the 9th Conf on Theoretical Aspects of Rationality and Knowledge (TARK 2003). New York: ACM, 2003: 72-87
[53]Zurel E, Nisan N. An efficient approximate allocation algorithm for combinatorial auctions[C]Proc of the 3rd ACM Conf on Electronic Commerce (EC 2001). New York: ACM, 2001: 125-136
[54]Vöcking B. A universally-truthful approximation scheme for multi-unit auctions[C]Proc of the 23rd Annual ACM-SIAM Symp on Discrete Algorithms (SODA 2012). New York: ACM, 2012: 846-855
[55]Dong Mo, Sun Gaofei, Wang Xinbing, et al. Combinatorial auction with time-frequency flexibility in cognitive radio networks[C]Proc of the 31st IEEE Int Conf on Computer Communications (IEEE INFOCOM 2012). Piscataway, NJ: IEEE, 2012: 2282-2290
[56]Shi Weijie, Zhang Linquan, Wu Chuan, et al. An online auction framework for dynamic resource provisioning in cloud computing[C]Proc of the 2014 ACM Int Conf on Measurement and Modeling of Computer Systems (SIGMETRICS 2014). New York: ACM, 2014: 71-83
[57]Zhang Hong, Li Bo, Jiang Hongbo, et al. A framework for truthful online auctions in cloud computing with heterogeneous user demands[C]Proc of the 32nd IEEE Int Conf on Computer Communications (IEEE INFOCOM 2013). Piscataway, NJ: IEEE, 2013: 1510-1518
[58]Feng Zhenni, Zhu Yanmin, Zhang Qian, et al. TRAC: Truthful auction for location-aware collaborative sensing in mobile crowdsourcing[C]Proc of the 33rd IEEE Int Conf on Computer Communications (IEEE INFOCOM 2014). Piscataway, NJ: IEEE, 2014: 1231-1239
[59]Yang Dejun, Xue Guoliang, Fang Xin, et al. Crowdsourcing to smartphones: Incentive mechanism design for mobile phone sensing[C]Proc of the 18th Annual Int Conf on Mobile Computing and Networking (MobiCom 2012). New York: ACM, 2012: 173-184
[60]Wei Guiyi, Zhu Ping, Vasilakos A V. Cooperation dynamics on collaborative social networks of heterogeneous population
[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(6): 1135-1146
[61]Sheng Shangpin, Liu Mingyan. Profit incentive in a secondary spectrum market: A contract design approach[C]Proc of the 32nd IEEE Int Conf on Computer Communications (IEEE INFOCOM 2013). Piscataway, NJ: IEEE, 2013: 836-844
[62]Jagannathan K, Menache I, Modiano E, et al. Non-cooperative spectrum access: The dedicated vs free spectrum choice[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(11): 2251-2261
[63]Osborne M J, Rubenstein A. A Course in Game Theory[M]. Cambridge, MA: MIT Press, 1994
[64]Fudenberg D, Tirole J. Game Theory[M]. Cambridge, MA: MIT Press, 1991
[65]Mas-Colell A, Whinston M D, Green J R. Microeconomic Theory[M]. Oxford, UK: Oxford Press, 1995
[66]Varian H. Economic mechanism design for computerized agents[C]Proc of USENIX Workshop on Electronic Commerce. Berkeley, CA: USENIX Association, 1995: 13-21
[67]Feng Xiaojun, Chen Yanjiao, Zhang Jin, et al. TAHES: Truthful double auction for heterogeneous spectrums[C]Proc of the 31st IEEE Int Conf on Computer Communications (IEEE INFOCOM 2012). Piscataway, NJ: IEEE, 2012: 3076-3080
[68]Zhou Xia, Zhang Zengbin, Wang Gang, et al. Practical conflict graphs for dynamic spectrum distribution[C]Proc of the ACM SIGMETRICS Int Conf on Measurement and Modeling of Computer Systems. New York: ACM, 2013: 5-16

Wu Fan, born in 1981. Associate professor and PhD supervisor. Member of China Computer Federation. His main research interests include wireless networking and mobile computing, algorithmic game theory and its applications, and privacy preservation.

Zheng Zhenzhe, born in 1989. PhD candidate. His main research interests include algorithmic game theory, resource management in wireless networking and data center (zhengzhenzhe@sjtu.edu.cn).
中图法分类号TP391
基金项目:国家“九七三”重点基础研究发展计划基金项目(2014CB340303);国家自然科学基金项目(61422208,61472252, 61272443,61133006);上海市科学技术委员会基金项目(15220721300)
收稿日期:2015-07-13;修回日期:2015-10-26
This work was supported by the National Basic Research Program of China (973 Program) (2014CB340303), the National Natural Science Foundation of China (61422208,61472252,61272443,61133006), and Shanghai Science and Technology Fund (15220721300).
