高中数学教学中“通解通法”能力的培养



高中数学教学中“通解通法”能力的培养

◇山东孙娜

在高中数学课堂教学中,注重学生“通解通法”能力的培养,不仅有利于学生快速抓住知识点的本质,有效形成系统的知识网络与结构,而且有利于学生消除或缓解对数学学科的畏惧心理,增强学生学习数学的自信．结合多年教学实践,笔者认为,要想促进学生数学“通解通法”能力的有效养成,在实际教学过程中,可从以下3方面着手.

1注重一法多用

这里的“一法”,不是特指某一种方法,也不是灵机一动、颇具技巧的某种解题妙法,而是最基本、最重要、最自然的通法．因此,在数学解题教学过程中,教师应注重一法多用的引导,运用学生常用的、常规方法来解决一类问题,将整个数学思维过程充分显示出来,从而帮助学生掌握数学解题的核心与精髓．

例如，在高中数学解题中,待定系数法是一项应用十分广泛的解题方法,常见类型有：1) 求圆的方程; 2) 求函数解析式; 3) 求圆锥曲线方程; 4) 等差、等比数列的基本运算; 5) 已知三角函数性质求参数．

若f(f(0))=4a,则实数a等于________.

以上2个例题均采用待定系数法进行求解,由此可见,采用“一法多用”进行教学,能够引导学生在解题时自觉发现、探索、总结、应用解题规律,培养归纳推理和演绎推理能力．

2注重常规方法的合理运用

纵观近年的高考数学命题,不难发现,发挥数学作为基础学科的重要作用,是数学命题的重要方向之一．考察学生数学基本方法的掌握情况以及数学基本能力的形成情况,是高考数学命题的核心所在．为此,在高中数学解题教学过程中,教师必须注重常规方法的运用,以不变应万变．

例如,对于处理立体几何的解答题,通常运用2种常规方法：1)传统法求解；2)建立空间直角坐标系法求解．就命题角度而言,往往鼓励学生运用建立空间直角坐标系法进行求解．但要注意,基于立体几何问题的核心在于学生空间想象能力与逻辑推理能力的培养,我们在提倡运用建立空间直角坐标系法来求解立体几何问题的同时,又不能过分依赖它,最终应根据实际需要来决定运用哪种常规方法求解更为便捷、高效．

3注重数学知识体系的有效构建

数学是一门逻辑严密的自然学科,在实际学习过程中往往涉及诸多的概念、公式、定理等．积极构建清晰、系统的知识网络,是培养学生数学“通解通法”能力的重要途径之一．因此,在实际教学过程中(尤其是高三复习阶段),数学教师应注重引导学生将重点知识、主干知识有序地串联在一起,形成一个系统的知识体系．

例如,在高三复习阶段,根据有关角的定义,笔者引导学生对高中阶段常见求角方法进行了总结,形成了如表1所示的知识体系．

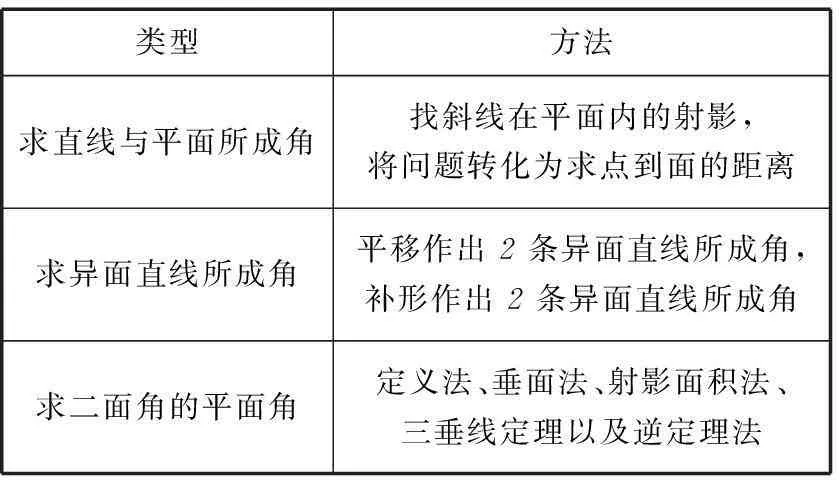
表1

在总结出高中阶段常见的求角方法之后,学生们又发现,以上3种类型均可运用建立空间直角坐标系的方法来进行求解,并且还节省了作角的过程,更为便捷．通过知识体系的有效建立,学生对通解通法的运用更加熟练,数学解题效率有了很大提高．

总之,广大高中数学教师在实际教学过程中应充分重视和大力提倡“通解通法”,将求解数学问题的最基本、最本质的方法充分挖掘出来,从而实现举一反三、事半功倍．

(作者单位：山东省邹平县第一中学)