基于Xu-White模型的横波速度预测

窦　龑，高　刚，梁　琳，谢晓庆，彭　锐（.长江大学a.油气资源与勘探技术教育部重点实验室，b.地球物理与石油资源学院，武汉000；.北京中油瑞飞信息技术有限责任公司，北京00007；.中海石油（中国）有限公司深圳分公司研究院，广州500；.中国石油集团长城钻探工程公司苏丹项目部，北京000）



基于Xu-White模型的横波速度预测

窦龑1，高刚1，梁琳2，谢晓庆3，彭锐4
（1.长江大学a.油气资源与勘探技术教育部重点实验室，b.地球物理与石油资源学院，武汉430100；
2.北京中油瑞飞信息技术有限责任公司，北京100007；3.中海石油（中国）有限公司深圳分公司研究院，广州510240；4.中国石油集团长城钻探工程公司苏丹项目部，北京100101）

摘要：在叠前地震属性分析和叠前地震反演中，若缺失横波信息，将会降低解释精度，对油气勘探造成不利影响。因此，预测横波速度就显得十分重要。与各种预测横波速度的方法相比，Xu-White模型综合考虑孔隙度、密度、泥质含量等因素的影响，符合砂、泥岩地层的实际情况，具有较高的预测精度。但由于砂、泥岩孔隙纵横比难以在实验室测得，使Xu-White模型的应用受到限制。在对Xu-White模型研究的基础上，通过引入模拟退火算法和粒子群算法寻求最优解，避免了搜索过程陷入局部极小解，提高了横波速度预测的精度。该方法在大港油田的实际资料处理中取得了较好的效果。

关键词：横波速度预测；粒子群算法；Xu-White模型；模拟退火算法

地震横波速度对流体识别、岩石物理参数的求取有着重要的作用，也是叠前地震反演、叠前地震属性分析中必备的基础资料，有利于提高储集层地震预测及油气检测的精度。然而，地震横波勘探和横波测井技术，因种种原因未能得到广泛的应用。因此，在缺少横波速度资料时，用纵波速度和其他储集层参数来预测横波速度就显得十分重要[1]。

目前，横波速度预测方法主要分为经验公式法和岩石物理模型法2大类。

经验公式法主要是利用孔隙度、密度、纵波速度、泥质含量、岩石矿物成分等参数来拟合横波速度。文献［2］—文献［5］给出了针对不同地区不同岩性的纵、横波速度拟合的经验公式。经验公式法具有简单、快速的特点，但由于不同地区地质特征的差异，其预测精度较差。

岩石物理模型法具有坚实的理论基础，所涉及的参数往往具有明确的物理意义，但通常仅适用于符合一定假设条件的地层。文献［6］提?出的Xu-White模型，综合考虑了岩石基质、孔隙形状、泥质含量等因素，能够获得较好的横波速度预测效果。文献［7］在此基础上引入了信息合取反演算法，达到了较为理想的预测效果。文献［8］和文献［9］在Xu-White模型中，引入虚拟孔隙度和误差融合技术，提高了横波速度的预测精度。针对Xu-White模型中模量难以求取的问题，文献［10］提出对同一流体项采用不同的算法求取。文献［11］提出了自适应的横波速度提取方法。文献［12］通过数值模拟，证明了采用变化的孔隙纵横比估算出的横波速度更为精确。文献［13］针对塔中地区，认为在横波速度预测方面，Xu-White模型不仅适用于碎屑岩储集层，也适用于碳酸盐岩储集层。而文献［1］、文献［14］、文献［15］分别采用Greenberg-Castagna公式、经验公式法、多元线性拟合、临界孔隙度模型及Xu-White模型等多种方法，讨论了横波速度预测方法的影响因素。

笔者采用Xu-White模型法，针对砂、泥岩孔隙纵横比难以求取的问题，通过粒子群算法，以实测纵波速度为约束，采用循环迭代的方式求取适合的孔隙纵横比，进而计算出横波速度。为避免粒子群算法出现早熟现象，引入了具有突跳特性的模拟退火算法，增加了算法的可靠性。并根据大港油田的实际测井资料进行了横波速度估算，对其预测效果进行了对比分析，认为基于Xu-White模型的横波速度预测具有较高的精度。

1　方法原理

1.1基于Xu-White模型的横波速度计算原理

文献［16］和文献［17］提出如下假设：①介质为均匀介质，孔隙为球体或椭球体，均匀随机地分布在连续介质中，且孔隙中充满了另一种物质，此物质的弹性参数与介质的不同；②通过介质的弹性波波长远大于孔隙尺寸的特征长度。在此假设条件下，可根据弹性波散射理论推导出弹性模量的表达式，即K-T方程。但在实际地质条件下，只有在孔隙度极小的情况下，才能满足该方程的假设条件。文献［6］基于K-T方程，结合微分等效介质理论，提出Xu-White模型。

Xu-White模型假设岩石由砂质和泥质组成，岩石骨架的泊松比近似常量，认为孔隙的几何形状对地震波速度有较大的影响。用孔隙纵横比来描述孔隙的几何形状，与孔隙度及岩石基质的剪切模量和体积模量相结合，可以得出岩石骨架的体积模量（kdry）和剪切模量（μdry）的近似简化式：

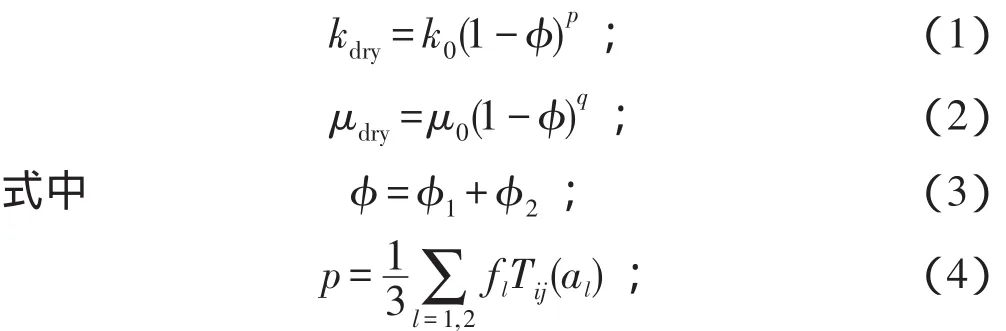
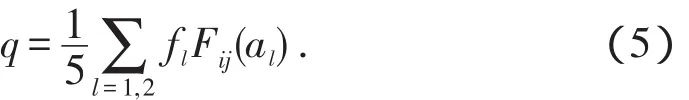
若已知干岩石的体积模量和剪切模量，就可以求出饱和流体岩石的体积模量和剪切模量[18]。

文献［18］假设在一个封闭的岩石流体系统中（即岩石表面没有流体流进流出），岩石中的所有孔隙都相通且充满流体，孔隙流体与岩石骨架间无物理或化学作用，岩石在宏观上均质，干岩石和饱和流体岩石的体积模量和剪切模量符合如下关系：

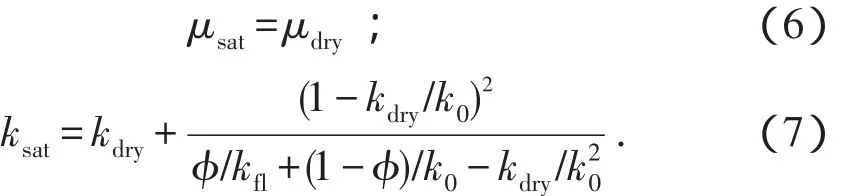
由经典岩石物理学公式可知，在已知岩石密度的情况下，地震波在均匀各向同性弹性介质中传播的纵、横波速度可表示为

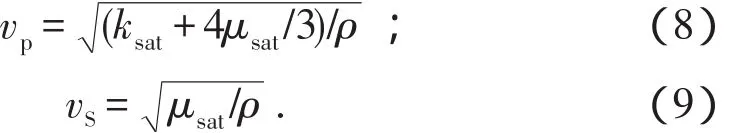
在Xu-White模型中，采用孔隙纵横比来描述砂岩和泥岩的孔隙形状。通常情况下，砂岩的孔隙纵横比大于泥岩孔隙纵横比。由于技术等方面的限制，孔隙纵横比难以实际测量，因此在实际计算中，通过与实测纵波速度对比，不断调整砂、泥岩孔隙纵横比参数，循环迭代计算，最终得到横波速度。其循环迭代的整个过程可简写为

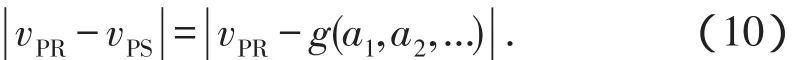
对此函数采用全局最优化方法，求取适合的砂、泥岩孔隙纵横比，使计算纵波速度接近实测纵波速度。最优化的算法很多，本文采用的是混合粒子群算法。

1.2混合粒子群算法原理

受鸟类觅食行为的启发，文献［19］提出了基于种群的粒子群算法。种群的每个成员可以抽象为一个粒子，而食物的位置就相当于是全局最优解。粒子有3个属性：位置、速度和适应度。粒子群算法与优化问题求解过程的相似性见表1.

表1　粒子群算法与优化问题求解过程比较

在实际应用中，首先通过已知条件来确定解空间的范围，其次将各粒子随机放入解空间。解空间的维数由求解的问题决定。解空间构造完成后，粒子的位置就可以用坐标的形式表示。根据所求问题构建适合的目标函数，并对每个粒子的适应度进行评价，根据粒子群的拓扑结构，确定粒子自身经历中的最佳位置和在整个种群中的最佳位置。粒子在解空间运动的速度受自身经历的最佳位置和种群中的最佳位置的影响，通过不断调节自身位置，向食物（全局最优解）运动。

假设解空间为N维，粒子数为D，在t时刻，第i个粒子的位置，速度，该粒子自身经历中的最佳位置，该粒子所在种群的最佳位置，则在t+1时刻，速度和位置坐标为从

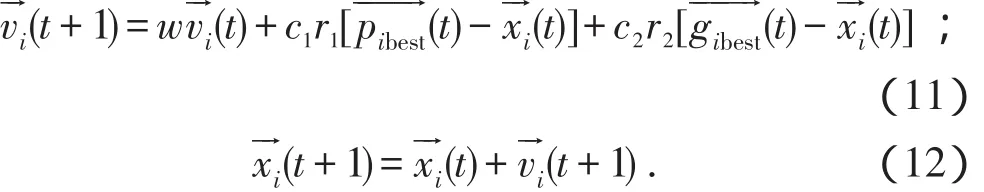
（11）式可以看出，3个部分决定了粒子新的位置和速度。右侧第1部分[ wvi(t) ]表示粒子先前速度的影响，通过惯性权重的调节，可以平衡全局和局部搜索，惯性权重越大，全局寻优能力越强，局部寻优能力越弱；第2部分（pibes）t表示粒子向自身学习的能力，亦称“自知部分”，反映了粒子局部搜索的能力；第3部分（gibes）t表示粒子向整个种群最优位置的学习，亦称“社会部分”。这3个部分共同决定了粒子在解空间的搜索能力。

粒子群算法具有实现简单、参数较少等优点，但当局部搜索能力占主导地位，多数粒子向少数居于当前种群最优位置的粒子聚集时，就会出现早熟现象。为避免这种现象的出现，在粒子群算法中引入具有概率突跳的模拟退火算法。这样，在整个搜索过程中，能够接受好的解，同时，能够以一定的概率接受坏的解，从而有效避免整个搜索过程陷入局部最小解。

1.3基于混合粒子群算法的横波速度计算流程

在实际岩石物理横波速度估算中，根据测井资料中目标层段的纵波速度、密度、孔隙度和泥质含量，选用适宜的岩石物理模型，求取流体和岩石基质的体积模量；利用Xu-White模型，计算出干岩石的体积模量和剪切模量；进而通过Gassmann方程，求取相应流体状态下的模量，最后算出横波速度。

基于混合粒子群算法的横波速度预测步骤如下。

（1）根据VRH模型[20]和Wood公式[21]，计算岩石基质和流体的体积模量，根据实际地质资料确定砂、泥岩的孔隙纵横比和泊松比的范围；

（2）确定种群数量，在解空间范围内随机初始化各粒子的位置和速度；

（3）基于Xu-White模型，以实测纵波速度进行约束，（10）式作为适应度函数，综合比较，得到当前粒子最优值pibest和种群最优值gibest；

（4）确定初始温度；

（5）计算当前温度下各粒子最优值的评价值，计算方法为

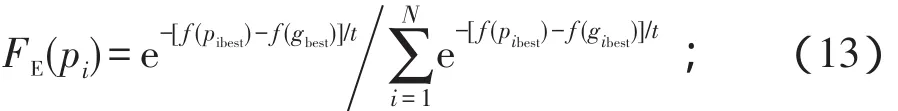
（6）基于各粒子的评价值，采用比例选择法更新种群最优值gibest；

（7）根据（11）式和（12）式，更新各粒子的速度和位置，计算此时的粒子最优值和种群最优值；

（8）采取退温操作，判断算法是否达到迭代次数，如果达到，算法停止，输出结果；否则转步骤5.

2　实例计算

采用本文方法，根据大港油田某井的实际测井资料，对相应层段进行了横波速度预测。实际测井曲线如图1所示。测井深度为2 650～2 700 m，目的层为砂、泥岩，密度为2.3～2.7 g/cm3，孔隙度为6%～12%，符合Xu-white模型的使用条件。目标层段为含水层。图2为纵、横波速度预测结果。从图2可以看出，计算纵波速度与实测纵波速度相差较小，采用本文方法估算的横波速度与实测横波速度总体特征基本一致，估算的横波速度绝对误差（实测横波速度与计算横波速度之差的绝对值）的最大值小于0.15 km/s，平均绝对误差0.08 km/s，平均相对误差（实测横波速度与计算横波速度之差与实测横波速度的比值）约为3.5%，能够满足实际工作的需要。

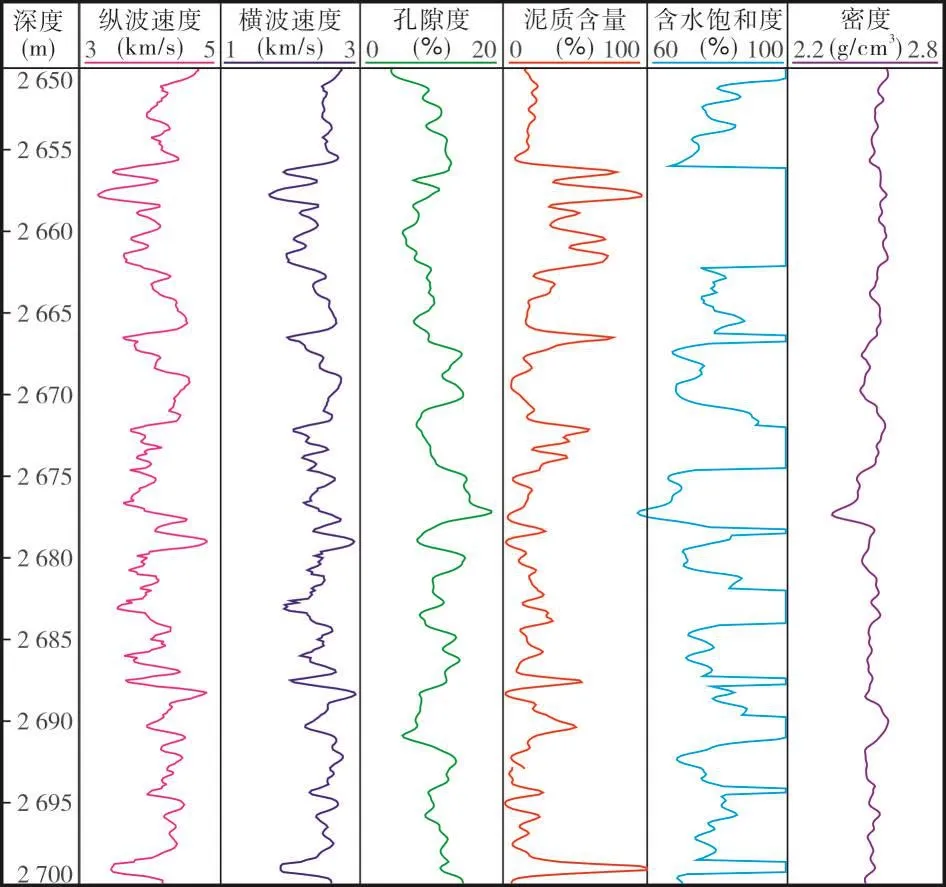
图1　实际测井数据

3　结语

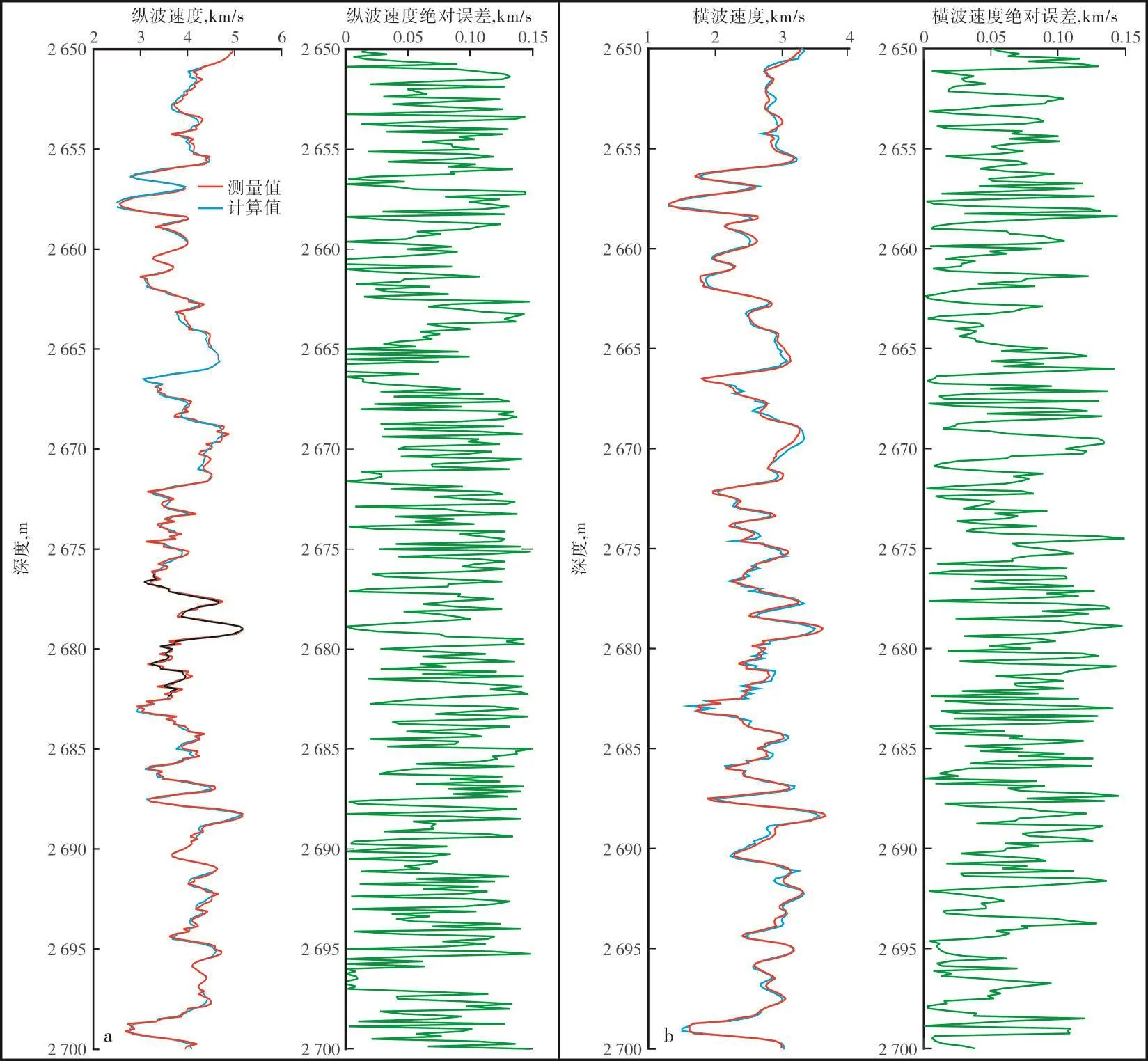
图2　纵波速度（a）、横波速度（b）预测值及绝对误差

Xu-White模型中涉及的参数较多，多个参数无法直接获得，使Xu-White模型的应用受到限制。本文采用实测纵波速度作为约束条件，通过对砂、泥岩孔隙纵横比和泊松比进行循环迭代，在粒子群算法中引入模拟退火算法，以比例选举法的方式选取种群的最优值，与标准粒子群算法相比，更易跳出局部最小值。计算横波速度与实测横波速度的误差小，能够满足生产的需要。

符号注释

al，a2——砂、泥岩的孔隙纵横比，f；

cl，c2——粒子的加速常数，通常在［0，2］之间取值，f；

fl，f2——分别为砂岩和泥岩的体积比，f；

g——用Xu-White模型求取纵波速度的函数；

k0——岩石基质的体积模量，GPa；

kdry——干岩石的体积模量，GPa；

kfl——流体的体积模量，GPa；

ksat——饱和流体岩石的体积模量，GPa；

p，q——与孔隙纵横比和泊松比有关的系数，f；

rl，r2——[0，1]之间均匀分布的随机数，f；

vP——均匀各向同性弹性介质中纵波速度，km/s；

vPR——实测纵波速度，km/s；

vS——均匀各向同性弹性介质中横波速度，km/s；

vPS——Xu-White模型估算出的纵波速度，km/s；

T，F——关于砂、泥岩孔隙纵横比的函数；

w——惯性权重；

ρ——岩石密度，g/cm3；

μ0——岩石基质的剪切模量，GPa；

μdry——干岩石的剪切模量，GPa；

μsat——饱和流体岩石的剪切模量，GPa；

ϕ——岩石总孔隙度，f；

ϕ1——泥岩孔隙度，f；

ϕ2——砂岩孔隙度，f.

参考文献：

［1］张元中，周开金，赵建斌，等.砂泥岩地层横波测井曲线预测方法研究［J］.石油物探，2012，51（5）：508-514.

ZHANG Yuanzhong，ZHOU Kaijin，ZHAO Jianbin，et al.Shear⁃wave logging curve prediction method for shaly sand formation［J］.Geophysical Prospecting for Petroleum，2012，51（5）：508-514.

［2］KEYS R G，XU Shiyou.An approximation for the Xu⁃White velocity model［J］.Geophysics，2002，67（5）：1 406 -1 414.

［3］李庆忠.岩石的纵、横波速度规律［J］.石油地球物理勘探，1992，27（1）：1-12.

LI Qingzhong.Velocity regularities of P⁃and S⁃waves in formations ［J］.Oil Geophysical Prospecting，1992，27（1）：1-12.

［4］CASTAGNA J P，BATZLE M L，EASTWOOD R I.Relationship be⁃tween compressional wave and shear wave velocities in clastic rocks ［J］.Geophysics，1985，50（5）：571-581.

［5］GREENBERG M L，CASTAGNA J P.Shear⁃wave velocity estima⁃tion in porous rocks：theoretical formulation，preliminary verifica⁃tion and application［J］.Geophysical Prospecting，1992，40（2）：195-209.

［6］XU Shiyou，WHITE R E.A physical model for shear⁃wave velocity prediction［J］.Geophysical Prospecting，1996，44（4）：687-717.

［7］张杨.利用Xu⁃White模型估算地震波速度［J］.成都理工大学学报（自然科学版），2005，32（2）：188-195.

ZHANG Yang.Xu White model for seismic wave velocity prediction ［J］.Journal of Chengdu University of Technology（Science & Tech⁃nology Edition），2005，32（2）：188-195.

［8］乔悦东，高云峰，安鸿伟.基于Xu⁃White模型的优化测井横波速度预测技术研究与应用［J］.石油天然气学报，2007，29（5）：100-102.

QIAO Yuedong，GAO Yunfeng，AN Hongwei.Study and application of optimal technique of shear⁃wave velocity prediction based on Xu⁃White model［J］.Journal of Oil and Gas Technology，2007，29（5）：100-102.

［9］王金伟，张尔华，谢春临.虚拟孔隙度优化Xu⁃White模型法预测横波速度［J］.断块油气田，2011，18（4）：445-448.

WANG Jinwei，ZHANG Erhua，XIE Chunlin.Prediction of shear wave velocity with optimized Xu⁃White model based on virtual po⁃rosity［J］.Fault⁃Block Oil & Gas Field，2011，18（4）：445-448.

［10］熊晓军，林凯，贺振华.基于等效弹性模量反演的横波速度预测方法［J］.石油地球物理勘探，2012，47（5）：723-727.

XIONG Xiaojun，LIN Kai，HE Zhenhua.A method for S⁃wave ve⁃locity estimation based on equivalent elastic modulus inversion［J］.Oil Geophysical Prospecting，2012，47（5）：723-727.

［11］林凯，贺振华，熊晓军，等.基于基质矿物模量自适应提取横波速度反演方法［J］.石油地球物理勘探，2013，48（2）：262-267.

LIN Kai，HE Zhenghua，XIONG Xiaojun，et al.S⁃wave velocity in⁃version based on adaptive extraction of matrix mineral modulus ［J］.Oil Geophysical Prospecting，2013，48（2）：262-267.

［12］白俊雨，宋志翔，苏凌，等.基于Xu⁃White模型横波速度预测的误差分析［J］.地球物理学报，2012，55（2）：589-595.

BAI Junyu，SONG Zhixiang，SU Ling，et al.The analysis of shear velocity prediction error by the Xu⁃White model［J］.Chinese Jour⁃nal of Geophysics，2012，55（2）：589-595.

［13］杨辉廷，敬兵，陈培元，等.塔中地区ZG5⁃7井区横波速度的预测［J］.天然气工业，2012，32（5）：25-27.

YANG Huiting，JING Bing，CHEN Peiyuan，et al.Prediction of S⁃wave velocity in the wellblock ZG5⁃7，middle Tarim basin［J］.Nat⁃ural Gas Industry，2012，32（5）：25-27.

［14］杨远，黄春梅，王宇航.川西Q地区须家河组横波预测方法研究［J］.吐哈油气，2012，17（3）：218-222.

YANG Yuan，HUANG Chunmei，WANG Yuhang.Study on shear wave prediction methods for Xujiahe formations in Q area of west Sichuan basin［J］.Tuha Oil and Gas，2012，17（3）：218-222.

［15］李文成，彭嫦姿，杨鸿飞.横波预测技术在YB地区的应用［J］.地球物理学进展，2014，29（4）：1 695-1 700.

LI Wencheng，PENG Changzi，YANG Hongfei.The application of S⁃wave prediction technology in YB area［J］.Progress in Geophys⁃ics，2014，29（4）：1 695-1 700.

［16］KUSTER G T，TOKSÖZ M N.Velocity and attenuation of seismic waves in two⁃phase media：Part 1：theoretical formulation［J］.Geophysics，1974，39（5）：587-606.

［17］KUSTER G T，TOKSÖZ M N.Velocity and attenuation of seismic waves in two⁃phase media：Part 1：experimental results［J］.Geo⁃physics，1974，39（5）：607-618.

［18］GASSMANN F.Elastic waves through a packing of spheres［J］.Geophysics，1951，16（4）：673-685.

［19］KENENDY J，EBERHART R C.Particle swarm optimization［C］//Proceeding of the IEEE International Conference on Neural Net⁃works.Perth，Austrilia，1995：1 942-1 948.

［20］HILL R.A self⁃consistent mechanics of composite materials［J］.Journal of the Mechanics and Physics of Solids，1965，13（4）：213-222.

［21］WOOD A W.A textbook of sound［M］.New York：The MacMillan Co.，1955：360.

（编辑叶良）

Prediction of S⁃Wave Velocity Based on Xu⁃White Model

DOU Yan1，GAO Gang1，LIANG Lin2，XIE Xiaoqing3，PENG Rui4
（1.Yangtze University，a.MOE Key Laboratory of Petroleum Resource and Exploration Technologies，b.College of Geophysics and Petroleum Resource，Wuhan，Hubei 430100，China; 2.CNPC Beijing Richfit Information Technology Co.，LTD，Beijing 100007，China;3.CNOOC Shenzhen, Guangzhou，Guangdong 510240，China；4.Sultan Project Department，Greatwall Drilling Company，CNPC，Beijing 100101，China）

Abstract：In the prestack inversion and prestack seismic attributes analysis，the lack of S⁃wave information usually leads to a bad influ⁃ence on petroleum exploration by decreasing accuracy of seismic data interpretation.Hence, Prediction of S⁃wave velocity by using other methods is more significant.Xu⁃White model，compared with other methods，comprehensively takes account of the influences of porosity，density and clay content，which is suitable for real sand⁃mudstone formation characterization with higher predictive accuracy.But the appli⁃cation of Xu⁃White model has been limited because the aspect ratio of the inclusion can not be measured in the laboratory.This paper stud⁃ies the Xu⁃White model，introduces simulated annealing algorithm and particle swarm optimization（PSO）to seek optimal solution，by which the local minimum solution is avoided during searching process，and the accuracy of S⁃wave velocity is obviously improved.The case study from real seismic data processing in an area of Dagang shows good results in application by using this method.

Keywords：S⁃wave velocity prediction; PSO algorithm; Xu⁃White model; simulated annealing algorithm

作者简介：窦龑（1989-），男，河南泌阳人，硕士研究生，地球物理勘探，（Tel）13557037116（E-mail）152325473@qq.com.

基金项目：国家自然科学基金（41074104）；中石油科技创新基金项目（2015D-5006-0301）

收稿日期：2015-05-10

修订日期：2015-09-23

文章编号：1001-3873（2016）01-0083-05

DOI：10.7657/XJPG20160116

中图分类号：P631.445.3

文献标识码：A